
はじめに
ロケットエンジンノズル-通過するガス流を音速を超える速度に加速するのに役立つ技術的な装置。 ノズルプロファイルの主なタイプを図に示します。
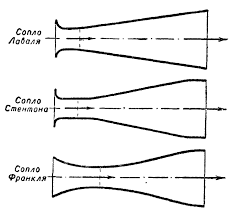
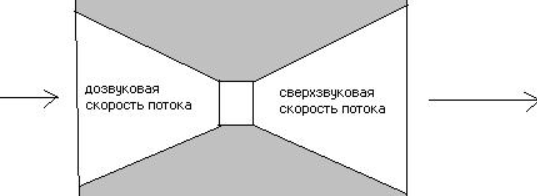
ガスの流れを加速する効率が高いため、ラバルノズルの実用的なアプリケーションが見つかりました。 ノズルは、中央が狭くなったチャネルです。 最も単純な場合、このようなノズルは、狭い端部と共役した一対の円錐台で構成されます。
ロケットエンジンでは、ラバルノズルは1915年にM.M.ポモルセフ将軍によって最初に使用されました。 1915年11月、M。M.ポモルセフ将軍は空力ミサイルのドラフトで空力研究所に連絡しました。
Pomortsevのロケットは圧縮空気で駆動されていたため、航続距離が大幅に制限されていましたが、沈黙していました。 ミサイルは敵の位置でtrenchから発射することを目的としていました。 弾頭にはTNTが装備されていました。
Pomortsevロケットでは2つの興味深い構造的ソリューションが使用されました。エンジンにはラバルノズルがあり、リングスタビライザーがボディに接続されていました。 現在、同様の設計が使用されていますが、すでに固体燃料エンジンと自動誘導システムが使用されています。

しかし、問題は古いままでしたが、すでに最大3 kmの限られた範囲の近代的な設計にあります。視界の良い条件で目標を目指して保持します。高コスト。
理論的背景
最新のロケットエンジンの効果的なノズルは、特別なガス力学計算に基づいてプロファイルされます。 断面積勾配、速度勾配、マッハ数に関連する基本的な方程式は次のとおりです。
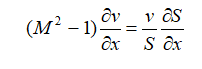
ここで、Sはノズル断面積です。 vはガス速度です。 Mはマッハ数(流れの任意のポイントでのガス速度と同じポイントでの音速の比)です。
この関係を分析すると、ラバルノズルで次の流れの状態を実現できることがわかります。
1)M <1-亜音速の入口での流れ:[1]
a)
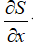 <0、その後
<0、その後 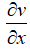 > 0(方程式から)。 狭いチャネル内の亜音速流が加速されます。
> 0(方程式から)。 狭いチャネル内の亜音速流が加速されます。
b)
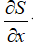 > 0、その後
> 0、その後 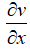 <0。 拡大するチャネル内の亜音速流が抑制されます。
<0。 拡大するチャネル内の亜音速流が抑制されます。
2)M> 1-超音速入力での流れ:
a)
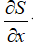 <0、その後
<0、その後 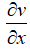 <0。 狭小流路内の超音速流は抑制されます。
<0。 狭小流路内の超音速流は抑制されます。
b)
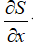 > 0、その後
> 0、その後 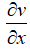 > 0。 拡大するチャネル内の超音速流が加速されます。
> 0。 拡大するチャネル内の超音速流が加速されます。
3)
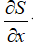 = 0-ノズルの最も狭いポイント、最小断面。
= 0-ノズルの最も狭いポイント、最小断面。
その後、M = 1(流れは音速を通過する)、または
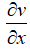 = 0(最高速度)。
= 0(最高速度)。
実際に実装されるモードは、ノズルの入口と環境の間の圧力差に依存します。
クリティカルセクションで到達した圧力が外部圧力を超える場合、ノズル出口での流れは超音速になります。 それ以外の場合、亜音速のままです。 [2]
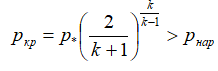 -超音速呼気の条件。
-超音速呼気の条件。
ここで、p *はブレーキ圧力(チャンバー内の圧力)です。 pcrは、ノズルのクリティカルセクションの圧力です。 p-環境の圧力; kは断熱指数です。
燃焼室のパラメーターがわかっている場合、ノズルの任意のセクションのパラメーターは、次の関係で見つけることができます。
圧力:
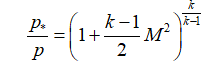 または
または 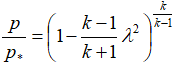 ;
;
温度:
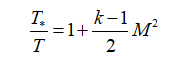 または
または 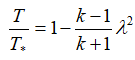 ;
;
密度:
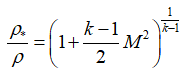 または
または 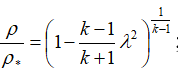 ;
;
速度:
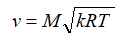 または
または 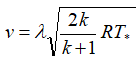 。
。
これらの式で、λは減速速度、特定のノズルセクションのガス速度と臨界セクションの音速の比、Rは特定のガス定数です。 インデックス「*」は、ブレーキパラメーター(この場合、燃焼室内のパラメーター)を示します。
問題の声明
1.ラバルノズル内のガス流のパラメーターを計算するには、このために、ラバルノズルのプロファイルを150の制御点に分割します-
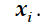 。 分割は、最小セクションがポイントに配置されるように実行されます
。 分割は、最小セクションがポイントに配置されるように実行されます 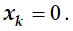 。 各セクションの圧力、密度、温度の気体力学関数の値が決定されます。
。 各セクションの圧力、密度、温度の気体力学関数の値が決定されます。
2.計算は、次の計算スキームとソースデータに従って、自由に配布される高レベルのPythonプログラミング言語を使用して実行されます。
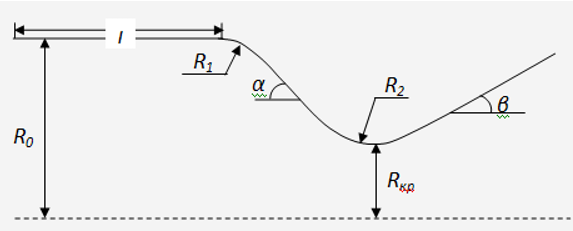
図1-ラバルノズルプロファイル
表1-ソースデータ
指定された初期データはデモンストレーション用です。
Pythonツールを使用したラバルノズルの計算
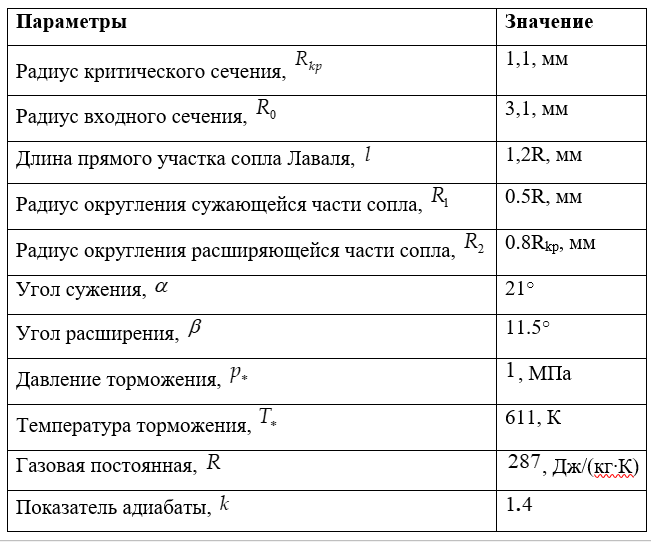
ラバルノズルのオリフィスのプロファイルと面積を構築するためのリスト
#!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' import numpy as np from math import * alfa=21.0# beta=11.5# rkr=1.1# R0=2*rkr r1=0.5*rkr# r2=0.8*rkr# ye=rkr+r2 L=1.2*R0# x0=0 y0=R0 xa=L ya=y0 xc1=xa yc1=ya-r1 xc=xa+r1*cos(radians(90-alfa)) yc=yc1+r1*sin(radians(90-alfa)) yd=ye-r2*sin(radians(90-alfa)) xd=xc+(yc-yd)/tan(radians(alfa)) xc2=xd+r2*sin(radians(alfa)) xe=xc2 xf=xe+r2*cos(radians(90-beta)) yf=ye-r2*sin(radians(90-beta)) def R(x): if x0<=x<=xa: return ya*1e-4 if xa<=x<=xc: return (yc1+sqrt(r1**2-(x-xc1)**2))*1e-4 if xc<=x<=xd: return (-tan(radians(alfa))*(x-xc)+yc)*1e-4 if xd<=x<=xf: return (ye-sqrt(r2**2-(x-xe)**2))*1e-4 if xf<=x: return (yf+tan(radians(beta))*(x-xf))*1e-4 y=[R(x+xe) for x in np.arange(-5,5,0.01)] x=np.arange(-5,5,0.01) plt.figure() plt.title(' ') plt.axis([-5.0, 5.0, 0.0, 3.0*10**-4]) plt.plot(x,y,'r') plt.grid(True) plt.figure() plt.title(' \n ') yy=[pi*R(x+xe)**2 for x in np.arange(-5,5,0.01)] plt.plot(x,yy,'r') plt.grid(True) plt.show()

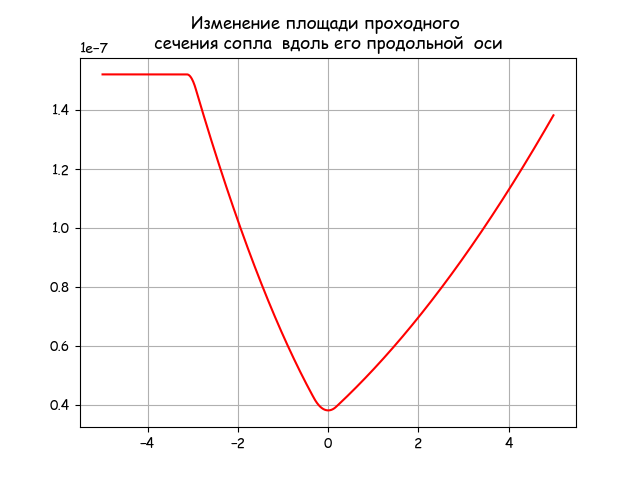
Pythonで問題を解決し続けるには、λ-減少したガス速度を縦軸に沿ったx座標に接続する必要があります。 これを行うには、SciPyライブラリのfsolve関数を次の命令で使用しました。
fsolve(<関数>、<開始点>、xtol = 1.5・10 ^ 8)
以下は、1つの開始点でソルバーを管理するためのプログラムのフラグメントです。
def lamda(z): m=round(Q(z),2) if z>= 0: x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,1.5) return x[0] if z<0: x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,0.5) return x[0]
これは、断熱指数kのべき乗関数を使用した複雑な代数方程式に対するPythonでの唯一の可能な解決策です。 たとえば、SymPyライブラリを使用する単純化された方程式の場合でも、1つのポイントに対してのみ無効な計算時間が得られます。
from sympy import * import time x = symbols('x',real=True) start = time.time() start = time.time() d=solve( 1.5774409656148784068*x *(1.0-0.16666666666666666667*x**2)**2.5-0.25,x) stop = time.time() print (" :",round(stop-start,3)) print(round(d[0],3)) print(round(d[1],3))
ソルバー時間 : 195.675
0.16
1.95
相対速度の気体力学関数を計算するためのリスト
#!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' import numpy as np from math import * from scipy.optimize import * import time start = time.time() alfa=21.0# beta=11.5# rkr=1.1# R0=2*rkr r1=0.5*rkr# r2=0.8*rkr# ye=rkr+r2 L=1.2*R0# x0=0 y0=R0 xa=L ya=y0 xc1=xa yc1=ya-r1 xc=xa+r1*cos(radians(90-alfa)) yc=yc1+r1*sin(radians(90-alfa)) yd=ye-r2*sin(radians(90-alfa)) xd=xc+(yc-yd)/tan(radians(alfa)) xc2=xd+r2*sin(radians(alfa)) xe=xc2 xf=xe+r2*cos(radians(90-beta)) yf=ye-r2*sin(radians(90-beta)) def R(x): if x0<=x<=xa: return ya*1e-4 if xa<=x<=xc: return (yc1+sqrt(r1**2-(x-xc1)**2))*1e-4 if xc<=x<=xd: return (-tan(radians(alfa))*(x-xc)+yc)*1e-4 if xd<=x<=xf: return (ye-sqrt(r2**2-(x-xe)**2))*1e-4 if xf<=x: return (yf+tan(radians(beta))*(x-xf))*1e-4 def S(x): return pi*R(x+xe)**2 xg=2*xe n=150 RG=287 # Tt=611 # k=1.4 def tau(x): return 1-(1/6)*x**2 def eps(x): return (1-(1/6)*x**2)**2.5 def pip(x): return 1-(1/6)*x**2 def Q(z): return S(0)/S(z) x=[x0-xe+(i/n)*(xg-x0) for i in np.arange(0,n,1)] def lamda(z): m=round(Q(z),2) if z>= 0: x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,1.5) return x[0] if z<0: x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,0.5) return x[0] plt.title(' ') y=[lamda(z) for z in x] stop = time.time() print (" :",round(stop-start,3)) plt.ylabel('λ(xi)- ' ) plt.plot(0, 1, color='b', linestyle=' ', marker='o', label=' ') plt.xlabel('xi - ') plt.plot(x,y,'r') plt.legend(loc='best') plt.grid(True) plt.show()
プログラム実行時間 : 0.222
結論:
得られたガス流速の分布図は、上記の理論に完全に対応しています。 同時に、提案されたアルゴリズムとライブラリによれば、150ポイントの計算時間は、sympyを使用した単一ポイントの計算時間の1000倍です。
気体動的温度関数を計算するためのリスト
#!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' import numpy as np from math import * from scipy.optimize import * import time start = time.time() alfa=21.0# beta=11.5# rkr=1.1# R0=2*rkr r1=0.5*rkr# r2=0.8*rkr# ye=rkr+r2 L=1.2*R0# x0=0 y0=R0 xa=L ya=y0 xc1=xa yc1=ya-r1 xc=xa+r1*cos(radians(90-alfa)) yc=yc1+r1*sin(radians(90-alfa)) yd=ye-r2*sin(radians(90-alfa)) xd=xc+(yc-yd)/tan(radians(alfa)) xc2=xd+r2*sin(radians(alfa)) xe=xc2 xf=xe+r2*cos(radians(90-beta)) yf=ye-r2*sin(radians(90-beta)) def R(x): if x0<=x<=xa: return ya*1e-4 if xa<=x<=xc: return (yc1+sqrt(r1**2-(x-xc1)**2))*1e-4 if xc<=x<=xd: return (-tan(radians(alfa))*(x-xc)+yc)*1e-4 if xd<=x<=xf: return (ye-sqrt(r2**2-(x-xe)**2))*1e-4 if xf<=x: return (yf+tan(radians(beta))*(x-xf))*1e-4 def S(x): return pi*R(x+xe)**2 xg=2*xe n=150 RG=287 # Tt=611 # k=1.4 def tau(x): return 1-(1/6)*x**2 def eps(x): return (1-(1/6)*x**2)**2.5 def pip(x): return 1-(1/6)*x**2 def Q(z): return S(0)/S(z) x=[x0-xe+(i/n)*(xg-x0) for i in np.arange(0,n,1)] def lamda(z): m=round(Q(z),2) if z>= 0: x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,1.5) return x[0] if z<0: x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,0.5) return x[0] plt.title(' ') t0=293 y=[ t0*tau(lamda(z)) for z in x] stop = time.time() print (" :",round(stop-start,3)) plt.ylabel('T(xi)- . ' ) plt.xlabel('xi - ') plt.plot(x,y,'r') plt.grid(True) plt.show()
プログラム実行時間:0.203
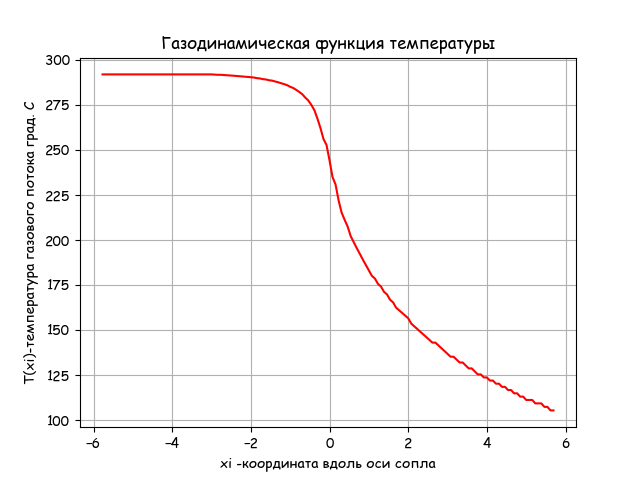
おわりに
ノズル出口の温度は、リストに示されている気体力学方程式に従って低下します。 プログラムの実行時間は許容範囲-0.203です。
テストインストール:

気体動圧関数を計算するためのリスト
#!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' import numpy as np from math import * from scipy.optimize import * import time start = time.time() alfa=21.0# beta=11.5# rkr=1.1# R0=2*rkr r1=0.5*rkr# r2=0.8*rkr# ye=rkr+r2 L=1.2*R0# x0=0 y0=R0 xa=L ya=y0 xc1=xa yc1=ya-r1 xc=xa+r1*cos(radians(90-alfa)) yc=yc1+r1*sin(radians(90-alfa)) yd=ye-r2*sin(radians(90-alfa)) xd=xc+(yc-yd)/tan(radians(alfa)) xc2=xd+r2*sin(radians(alfa)) xe=xc2 xf=xe+r2*cos(radians(90-beta)) yf=ye-r2*sin(radians(90-beta)) def R(x): if x0<=x<=xa: return ya*1e-4 if xa<=x<=xc: return (yc1+sqrt(r1**2-(x-xc1)**2))*1e-4 if xc<=x<=xd: return (-tan(radians(alfa))*(x-xc)+yc)*1e-4 if xd<=x<=xf: return (ye-sqrt(r2**2-(x-xe)**2))*1e-4 if xf<=x: return (yf+tan(radians(beta))*(x-xf))*1e-4 def S(x): return pi*R(x+xe)**2 xg=2*xe n=150 RG=287 # Tt=611 # k=1.4 def tau(x): return 1-(1/6)*x**2 def eps(x): return (1-(1/6)*x**2)**2.5 def pip(x): return 1-(1/6)*x**2 def Q(z): return S(0)/S(z) x=[x0-xe+(i/n)*(xg-x0) for i in np.arange(0,n,1)] def lamda(z): m=round(Q(z),2) if z>= 0: x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,1.5) return x[0] if z<0: x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,0.5) return x[0] plt.title(' ') p0=3.6 y=[ 3.6*pip(lamda(z)) for z in x] stop = time.time() print (" :",round(stop-start,3)) plt.ylabel('P(xi)- ' ) plt.xlabel('xi - ') plt.plot(x,y,'r') plt.grid(True) plt.show()
プログラム実行時間:0.203
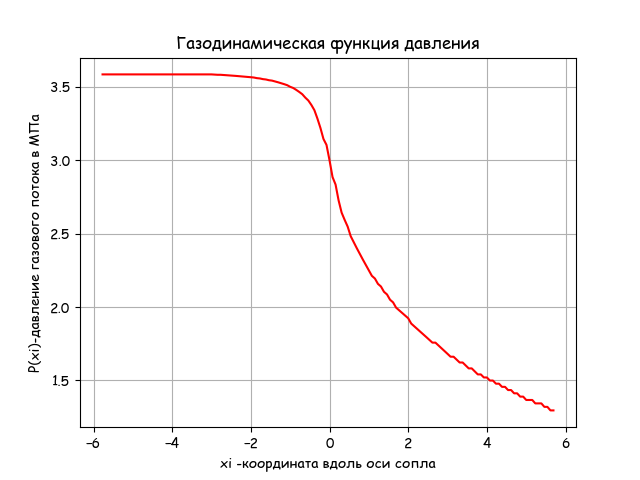
おわりに
リストに示されている気体力学方程式に従って、ノズル出口の圧力が低下します。 プログラムの実行時間は-0.203です。
ガス圧によるトラクションの発生を図に概略的に示します。
気体の相対密度の気体力学関数を計算するためのリスト
#!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' import numpy as np from math import * from scipy.optimize import * import time start = time.time() alfa=21.0# beta=11.5# rkr=1.1# R0=2*rkr r1=0.5*rkr# r2=0.8*rkr# ye=rkr+r2 L=1.2*R0# x0=0 y0=R0 xa=L ya=y0 xc1=xa yc1=ya-r1 xc=xa+r1*cos(radians(90-alfa)) yc=yc1+r1*sin(radians(90-alfa)) yd=ye-r2*sin(radians(90-alfa)) xd=xc+(yc-yd)/tan(radians(alfa)) xc2=xd+r2*sin(radians(alfa)) xe=xc2 xf=xe+r2*cos(radians(90-beta)) yf=ye-r2*sin(radians(90-beta)) def R(x): if x0<=x<=xa: return ya*1e-4 if xa<=x<=xc: return (yc1+sqrt(r1**2-(x-xc1)**2))*1e-4 if xc<=x<=xd: return (-tan(radians(alfa))*(x-xc)+yc)*1e-4 if xd<=x<=xf: return (ye-sqrt(r2**2-(x-xe)**2))*1e-4 if xf<=x: return (yf+tan(radians(beta))*(x-xf))*1e-4 def S(x): return pi*R(x+xe)**2 xg=2*xe n=150 RG=287 # Tt=611 # k=1.4 def tau(x): return 1-(1/6)*x**2 def eps(x): return (1-(1/6)*x**2)**2.5 def pip(x): return 1-(1/6)*x**2 def Q(z): return S(0)/S(z) x=[x0-xe+(i/n)*(xg-x0) for i in np.arange(0,n,1)] def lamda(z): m=round(Q(z),2) if z>= 0: x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,1.5) return x[0] if z<0: x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,0.5) return x[0] plt.title(' ') y=[ eps(lamda(z)) for z in x] stop = time.time() print (" :",round(stop-start,3)) plt.ylabel(' ' ) plt.xlabel('xi - ') plt.plot(x,y,'r') plt.grid(True) plt.show()
プログラム実行時間:0.203
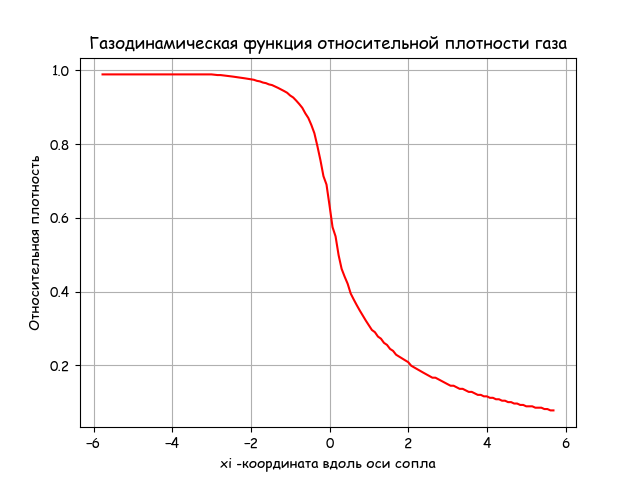
おわりに
ノズルの出口でのガス密度は、リストに示されているガスダイナミクスの式に従って減少します。 プログラムの実行時間は許容範囲です。
結論
- Pythonツールを使用して気体力学プロセスを記述するために使用される分数指数を使用して、非線形べき方程式の実根を解く方法が開発されました。 この方法は、scipyモジュールのfsolveソルバーの使用に基づいています。 最適化する。
- 開発された方法を使用して、以下の気体力学関数を決定して、現代のロケットエンジンのノズルを計算する実証問題。 温度 圧力 反応性ガスの密度。
参照資料
1. A. A.ドロフェエフ熱ロケットエンジンの理論の基礎(ロケットエンジンの一般理論)MSTU。 N.E.バウマンモスクワ1999
2. Landau L. D.、Lifshits E. M. Chapter X.圧縮性ガスの一次元運動。 §97.ノズルからのガス流出//理論物理学。 -T. 6.流体力学。