情報の削除を伴うコーディング。 パート2、数学

はじめに

前の部分では、キーとメッセージの共通部分を分離できる場合、元のメッセージよりも少ない情報を送信できるというコーディングの基本的な可能性について検討しました。

このトピックがどこから来たのかを少しお話ししましょう。 むかしむかし、 私は一人の善良な人からivladを取りましたが、これまでのところ、「暗号自体は置換と置換として知られる2つの方向に分けることができる」という興味深い本[1]を与えません（許して）。 。

したがって、ほぼすぐに次の質問が表示されました。

• なぜなら 再配置と置換は情報量を保存します。この制限を回避し、メッセージ内の情報よりも少ない情報を送信することは可能ですか？ここから（「弱くない」から）最初の部分が生まれました。
• 問題が解決可能と思われる場合、それ自体に解決策とその中の少なくとも数学的意味の一部があります-この質問はこの部分のトピックです。
• このすべてに実用的な意味はありますか？質問はまだ開かれています。

カラスと机の共通点は何ですか？

ここから写真を撮ります 。

タイトルのキャロルのなぞなぞは、解決する必要がある問題の例として与えられています。 つまり、関数のペアを定義する $$$E（k、m）$ -コーディングと $$$D（k、s）$ -次の条件を満たすデコード：

• $$$I（E（k、m））\ le I（m）$ –シャノンが送信した情報量は、元のメッセージの情報量よりも少ない
• $$$D（k、E（k、m））= m$ -エンコードされたメッセージに適用されるデコード機能は、元のメッセージを一意に復元します。

ここに $$$I（m）$ -メッセージ内のシャノン[2]に基づく情報量（すべての文字が平等に発生することを想定しています。これは一般的なケースでは正しくありませんが、表示を簡単にするために使用されます） $$$m$ 、 $$$k$ -キー $$$c = E（k、m）$ -エンコードされたメッセージ。

さらなる考察を簡素化するために、数値形式に縮小できるメッセージにさらに自分自身を制限してみましょう。これは一方では特に制限されません（すべての文字に対応する数値コードを割り当てることができるため）、他方では数学を使用することができます希望のボリューム。

そこで、最初に2つの数値を例として考えてみましょう $$$k = 746,130$ そして $$$m = 50133666$ 算術の基本定理[4]（任意の自然数は単純な積に分解できる）を使用すると、次のパラメーターが見つかります。

• 最小公約数 $$$k$ そして $$$m$ - $$$GCD（k、m）= $ 1,25$ その単純な除数 $$$[2,3,11,19]$ 、
• プライベート $$$m / gcd（k、m）= $ 59$ およびその単純な除数 $$$[5,7,17​​]$ 、これを $$$s_0$ 、
• 番号拡張 $$$m$ 素因数による： $$$[2,3,11,19,39,979]$ 、
• 番号拡張 $$$k$ 素因数による： $$$[2,3,5,7,11,17,19]$ 。

これらすべてをテーブル形式で記述します。キーとメッセージの間の情報の共通部分は青でマークされ、黄色はキーに固有の情報、オレンジはメッセージに固有です。

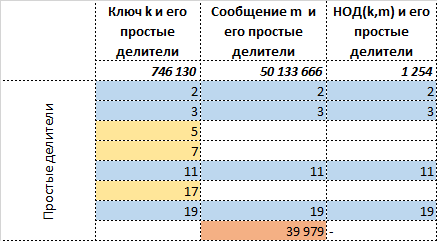
すぐに明らかになります $$$GCD（k、m）$ キー間の共通部分です $$$k$ とメッセージ $$$m$ 、送信者と受信者の両方です。 したがって、理想的にはもちろん、実際にはそうではありませんが、以下に関する情報を伝えるだけで十分です。

• メッセージ情報に固有-適用されません $$$k$ つまり $$$[39 979]$ すなわち $$$s_0 = $ 39,99$ 、

• ほとんどの $$$GCD（k、m）$ しかし、それは復元できなかったためです。

単純な除数の位置をマークしましょう $$$GCD（k、m）$ 単純な仕切りと共通 $$$k$ 、単位、および残りは、ただし、先頭の位置である場合があります-ゼロ。

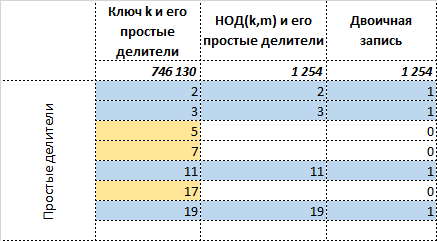
結果の数 $$$s_1 = 1010011 = 83$ 十分に特徴づける $$$GCD$ 、それにより、元のメッセージを復元できます。 すなわち 入力で2つの数値を取得する $$$[39 979、83]$ かなり単純な逆変換を行う必要があります。







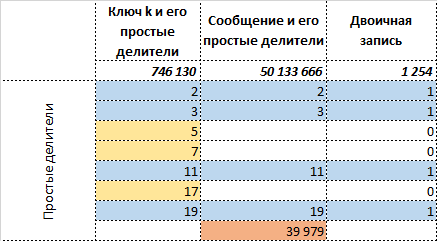
今、バイナリ形式で元のメッセージの長さを評価する場合 $$$len_2（m）= len_2（[1111010000011100100000100]）= 26$ とメッセージ $$$len_2（[c_0、c_1]）= len_2（[1001110000101011、1010011]）= 23$ 、メッセージの長さを節約できることがわかります $$$3$ ビット、情報量と同じ $$$I（m）= 13$ 少し $$$I（c）= I（[c_0、c_1]）= 11.5$ ビット。 ここに関数があります $$$len_2（\ cdot）$ -バイナリ形式の数値の長さ。







したがって、有名なジョークの言葉では、「スコットランドには少なくとも片側に黒い羊が少なくとも1匹います」[3]。



そのため、現時点で持っているもの-このエンコード方法は適切ですが 、展開で同じ除数を持つ数のペアにのみ適しています。 そうでない場合、たとえば、プライムをキーおよびメッセージとして使用する場合、明らかに何も減らすことはできません。メッセージの長さおよび送信される情報の量を増やすだけで、これは私たちが達成したことではありません。 たとえば、次の場合にも同じ状況が繰り返されます。 $$$GCD（k、m）<2$ または $$$len_2（c_1）≥len_2（GCD（k、m））$ なぜなら 節約は原則的に最小限か、またはありません。

何をすべきか...

このコーディング方法で成功する可能性を高めるために？

一般に、キーを注意深く見ると、それは素数にうまく分割されていることがわかります $$$2,3,5,7,11,17,19$ 、検索操作の成功のために特別に行われた $$$GCD（k、m）$ 。 このような操作は、使用されるキーの数に悪影響を及ぼし、単純な要因のシーケンスを決定し、それをキー情報の一部にするため、急進的ではありませんが、エンコードオプションの数を増やして、キーの数にプラスの影響を与えます。 キーの代わりに使用することは数字ではありません $$$[746 130]$ そしてカップル $$$[746 130、0125763]$ ここで、2番目の数値は乗算の順序を反映し、値を決定します $$$c_1$ 。

効果的に解決する必要がある次の問題は、素数と2のべき乗の発生頻度の比率です。2のべき乗による符号化効率は、長さが長くなると非常に急速に低下することがわかります。 $$$c_1$ （共通の単純な除数が1つある場合は、対応するシーケンスのグラフを参照してください）、主にキーの除数とその値に依存します。

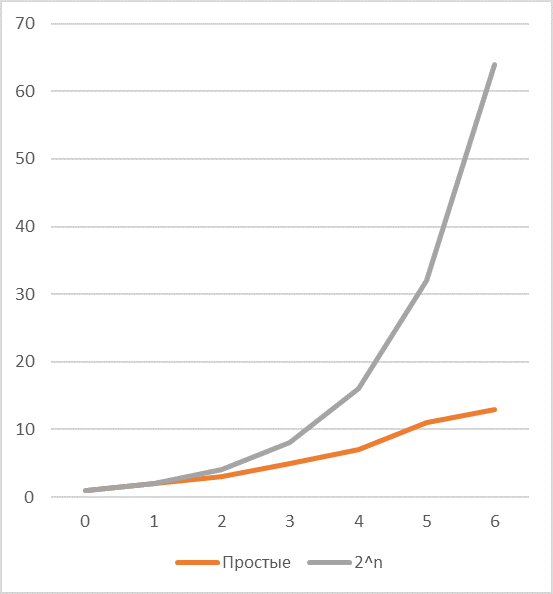
たとえば、2つの一般的な除数があり、そのうちの1つが次と等しい場合 $$$3$ 、それから貯蓄の機会は非常に顕著に増加します。







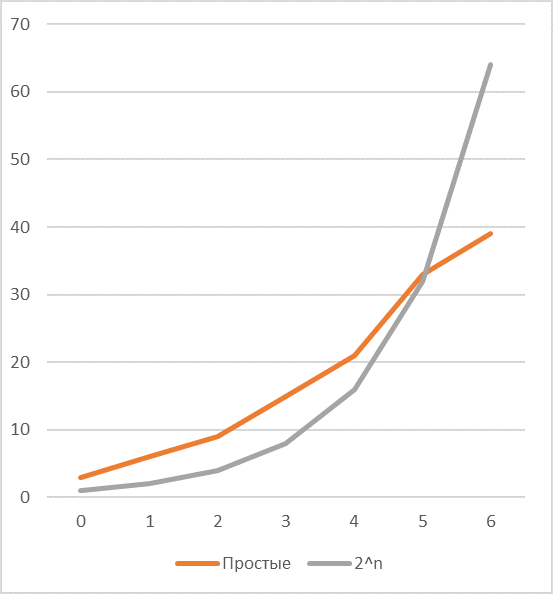
つまり、効率的なコーディングを行うには、より効率的なコーディング方法を考え出す必要があります。 $$$c_1$ 。

つまり、トピックはさらに掘り下げる意味があります。

例

通常github [5]に投稿されているように-Excelが使用されている理由は 多くの人がそれを持っているので、互換性について考える必要はありません。 ファイルには2つのブックマークがあります。

• 「テスト」 -計算自体など Excel関数「CASE BETWEEN（）」をかなり積極的に使用し、キーとメッセージの番号は比較的単純な場合があります。目的の節約を得るには、いくつかのセルに何度か足を踏み入れてenter
  
  
  
  キーを押す必要があります（31-36行目で結果）。
• 「例1」 -既製の計算の例を示します。 Excelのランダム性により、繰り返しの機会がなくなります。

参照資料

1. シン・サイモン。 暗号の本。 暗号とその解読の秘密の歴史。 M.アストレル2007。
2. https://en.wikipedia.org/wiki/%D0%98%D0%BD%D1%84%D0%BE%D1%80%D0%BC%D0%B0%D1%86%D0%B8%D0 ％BE％D0％BD％D0％BD％D0％B0％D1％8F_％D1％8D％D0％BD％D1％82％D1％80％D0％BE％D0％BF％D0％B8％D1％8F
3. http://www.gaelic.ru/Biblioteka/Folklore/anekdoty.htm
4. https://en.wikipedia.org/wiki/%D0%9E%D1%81%D0%BD%D0%BE%D0%B2%D0%BD%D0%B0%D1%8F_%D1%82%D0 ％B5％D0％BE％D1％80％D0％B5％D0％BC％D0％B0_％D0％B0％D1％80％D0％B8％D1％84％D0％BC％D0％B5％D1％82 ％D0％B8％D0％BA％D0％B8
5. https://github.com/rumiantcev/nod_code