GPUデータの並列ソート

この記事では、 並列ソートの概念を紹介します。 ピクセルを並べ替えるシェーダーの理論と実装について説明します。

はじめに

80年代または90年代にコンピューター理論を学んだ場合、 ソートアルゴリズムで驚くべきことを開発者が理解するのに一生懸命努力した可能性があります。 最初は取るに足りないタスクのように見えるものが、コンピュータサイエンスの基礎であることが判明しました。



しかし、ソートアルゴリズムとは何ですか？ 数字のリストがあると想像してください。 ソートアルゴリズムは、このリストを取得し、リスト内の数値を並べ替えるプログラムです。 ソートアルゴリズムの概念は、 計算の複雑さを研究する際にしばしば導入されます。これは、今後の記事で詳しく説明する別の広大な知識の領域です。 アイテムのリストを並べ替える方法は無限にあり、各戦略はコストと速度の間で独自のトレードオフを提供します。



ソートアルゴリズムの複雑さのほとんどは、問題の定義方法とその解決方法に起因しています。 要素の順序を変更する方法を決定するには、アルゴリズムで数値を比較する必要があります。 科学的な観点からは、比較を行うたびにアルゴリズムの複雑さが増します。 難易度は、実行された比較の数によって測定されます。



ただし、すべてがそれほど単純ではありません。要素の比較と置換の数は、リスト自体に依存します。 そのため、コンピューターの理論では、アルゴリズムのパフォーマンスを評価するより効果的な方法があります。 アルゴリズムの最悪のシナリオは何ですか？ 彼が作業できる最もソートされていないリストをソートするための最大ステップ数は？ この問題の見方は、 最悪の場合の分析として知られています。 最良のシナリオで同じ質問をすることができます。 配列をソートするためにアルゴリズムが実行しなければならない比較の最小数は何ですか？ 単純化するために、最後のタスクは、多くの場合、 「O」largeという指定を参照します。これは、ソートされる要素の数の関数として複雑さを測定します $$$n$ 。 そのような条件下では、どのアルゴリズムもより速く実行できないことが証明されています $$$\ mathcal {O} \左（n \ log n \右）$ 。 これは、長さの入力配列を常にソートするアルゴリズムが存在できないことを意味します $$$n$ より少ないことで $$$n \ log n$ 比較。

GPUの制限

従来のソートアルゴリズムは、2つの基本概念に基づいて作成されます。

• 比較 ：リストの2つの要素を比較し、どちらが大きいかを判断する操作。
• 置換 ：2つの要素を再配置して、リストを必要なものに近い状態にします。

ソートされるリストは、多くの場合配列として指定されます。 配列の任意の要素へのアクセスは非常に効率的であり、制限なしで任意の2つの要素を交換できます。



並べ替えにシェーダーを使用する場合は、まず新しい環境の固有の制限に対処する必要があります。 数値のリストをシェーダーに渡すことはできますが、これはその並列処理を使用する最良の方法ではありません。 概念的には、GPUが各ピクセルに対して同じシェーダーコードを同時に実行すると想像できます。 ビデオプロセッサには、各ピクセルの計算を並列化するための十分な処理能力がない可能性が高いため、通常、これは発生しません。 画像の一部は並行して処理されますが、どの特定の部分について推測するべきではありません。 したがって、シェーダーコードは、実際には常にこの方法で実行されるとは限らない場合でも、 真の並列処理の同じ制限の下で実行する必要があります。



ただし、より深刻な制限は、シェーダーコードがローカライズされることです。 GPUが座標でピクセルのコードの一部を実行している場合 $$$\左[x、y \右]$ 、その後、他のピクセルに書き込むことはできません $$$\左[x、y \右]$ 。 シェーダーでは、スワップ操作には両方のピクセルの同期が必要です。

GPUソート

この記事で紹介するアプローチの概念は単純です。

• ソートされたデータはテクスチャとして送信されます。
• 配列がある場合 $$$n$ 要素、サイズのテクスチャを作成します $$$n \回1$ ピクセル数
• 各ピクセルの赤チャンネル値には、ソート可能な数値が含まれています。
• 各レンダリングパスは、配列を最終状態に近づけます。

たとえば、ソート用の4つの数字のリストがあると想像してみましょう。 $$$\左[4,3,2,1 \右]$ 。 テクスチャを作成してシェーダーに渡すことができます $$$4 \回1$ ピクセル、値を赤チャンネルに保存：









前述のように、シェーダーで実行するときに場所を変更する操作は、2つの独立したピクセルによって並行して実行する必要があるため、はるかに複雑です。 この制限を処理する最も簡単な方法は、隣接するピクセルのペアを交換することです。









CPUでの実行と比較して、プロセスはほぼ逆の順序で実行されることを追加することが重要です。 最初のピクセルは前の値をサンプリングします。 $$$4$ 右側の値 $$$3$ 。 置換のペアの左側にあるため、より小さい値を受け入れる必要があります。 2番目のピクセルは、反対の操作を実行する必要があります。



これらの計算は互いに独立して実行されるため、コードの両方の部分は、値が低いほど低い通信なしで「同意」する必要があります。 これは並列ソートの複雑さです。 注意しないと、置換ペアの両方のピクセルが同じ数を取得するため、複製されます。



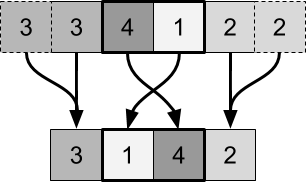
交換プロセスを繰り返しても、何も変わりません。 各ペアは1ステップでソートできます。 このプロセスを再現しても、変更は発生しません。 これに対処するには、置換ペアを変更する必要があります。 これは次の図で確認できます。













画像全体がソートされるまで、これらの2つのステップを交互に使用できます。









この手法は長い間存在しており、多くのスタイルとバリエーションで実装されています。 置換ペアには奇数/偶数および偶数/奇数のインデックスがあるため、これはしばしば偶奇ソートと呼ばれます。 この動作メカニズムはバブルソートに深く関係しているため、アルゴリズムが「 パラレルバブルソート」と呼ばれることは驚くことではありません。

難易度

ビデオプロセッサを使用する場合、ピクセルごとに同じシェーダーコードが同時に実行されると想定する必要があります。 従来のCPUでは、各比較/置換を個別の操作と見なす必要があります。 シェーダーパスが考慮されます $$$n$ 操作。 それらをすべて並行して計算できると仮定すると、1つの実行時間と実行 $$$n$ 同じになります。 したがって、各シェーダーパスの並列の複雑さは $$$1$ 。



最悪の場合の難しさは何ですか？ 各ステップでピクセルが最終位置に移動することがわかります。 最大ピクセル移動は $$$n$ 、つまり、リストをソートするためにこれ以上は必要ありません $$$n$ ステップ。



このタスクをより伝統的な観点から見ると、すべてがより複雑になります。 各シェーダーパスは、各ピクセルを少なくとも1回分析します。つまり、複雑さが増します。 $$$n$ 。 パス数と組み合わせて $$$n$ これは複雑さをもたらします $$$\ mathcal {O} \左（n ^ 2 \右）$ 。 これは、シーケンシャル実行での偶奇ソートがいかに効果的でないかを示しています。

パート2.シェーダーの実装。

シミュレーションシェーダー

シェーダーは通常、送信するテクスチャを処理するために使用されます。 それらの作業の結果は画面上に視覚化され、テクスチャ自体は変更されません。 この記事では、シェーダーが同じテクスチャーで繰り返し動作するようにしたいので、何か違うことをしたいと思います。 これについては、前の「シミュレーションにシェーダーを使用する方法」のシリーズで詳しく説明しました。



アイデアは、2つのレンダーテクスチャを作成することです。シェーダーで変更できる特別なテクスチャです。 次の図は、このプロセスの仕組みを示しています。









2つのレンダーテクスチャは周期的にスワップされるため、シェーダーパスは前のテクスチャを入力として使用し、2番目のテクスチャを出力として使用します。



この記事では、「シェーダーをシミュレーションに使用する方法」投稿で紹介した実装を使用します。 まだ読んでいなくても心配しないでください。 アルゴリズム自体のみに焦点を当てます。次のことを知る必要があります。

float4 frag(vertOutput i) : COLOR { //  X, Y  [0, _Pixels-1] float2 xy = (int2)(i.uv * _Pixels); float x = xy.x; float y = xy.y; // UV-  [0,1] float2 uv = xy / _Pixels; // UV-   float s = 1.0 / _Pixels; ... }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

シェーダーのフラグメント関数には、ソートコードが含まれます。 uv



変数は、現在レンダリングされているピクセルのUV座標を示し、 s



はUV空間のピクセルサイズを表します。

交換ペアの並べ替え

前のパートでは、 置換ペアの概念を紹介しました。 ピクセルはペアでグループ化され、単一のシェーダーパスでソートされます。 色が隣接する2つのピクセルを想像してみましょう $$$x$ そして $$$y$ 2つの数字です。 シェーダーパスはこれら2つのピクセルをサンプリングし、それに応じて順序を変更する必要があります。









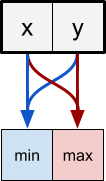
これを行うには、スワップペアの左側のピクセルが2ピクセル高くサンプリングし、最終的な色を選択します $$$min \左（x、y \右）$ 。 右側のピクセルは反対のことを行います。









ピクセル位置は、実行する必要がある操作だけでなく、サンプリングされたピクセルも決定します。 最小ピクセルは、現在の位置とその右側のピクセルをサンプリングする必要があります。 最大ピクセルは、左側のピクセルをサンプリングする必要があります。

 //  max float3 C = tex2D(_MainTex, uv).rgb; //   float3 L = tex2D(_MainTex, uv + fixed2(-s, 0)).rgb; //   result = max(L, C); //  min float3 C = tex2D(_MainTex, uv).rgb; //   float3 R = tex2D(_MainTex, uv + fixed2(+s, 0)).rgb; //  result = max(C, R);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

さらに、最小ピクセルと最大ピクセルは各操作の後に交換されます。 次の図は、最小操作を実行するピクセル（青）と最大操作を実行するピクセル（赤）を示しています。









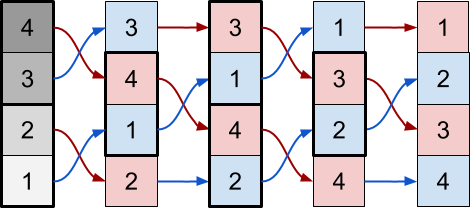
実行する操作を選択する際の2つの決定要因は、反復回数 _Iteration



と要素 x



（ _Iteration



ではなく列をソートする場合はy



インデックスです 。



上の図を見ると、実行すべき操作を決定できる最後の条件を引き出すことができます-最小または最大：

 //  / #define EVEN(x) (fmod((x),2)==0) #define ODD(x) (fmod((x),2)!=0) float3 C = tex2D(_MainTex, uv).rgb; //  if ( ( EVEN(_Iteration) && EVEN(x) ) || ( ODD (_Iteration) && ODD (x) ) ) { //  max float3 L = tex2D(_MainTex, uv + fixed2(-s, 0)).rgb; //  result = max(L, C); } else { //  min float3 R = tex2D(_MainTex, uv + fixed2(+s, 0)).rgb; //  result = min(C, R); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この条件により、偶数回（2番目、4番目、...）の間に、偶数位置のピクセルが最大演算を実行し、奇数位置のピクセルが最小演算を実行します。 奇数回（1回目、3回目、...）で逆のことが起こります。



この効果を機能させるには、シェーダーコードにテクスチャ外のピクセルへのアクセスを妨げる境界条件がないため、両方のレンダリングテクスチャをClampに設定する必要があります。

おわりに

他の並べ替えアニメーションはこのギャラリーで見つけることができます：





[注 per。：Patreonの著者のページでは、シェーダーのStandardバージョンとPremiumバージョンを有料でダウンロードできます。]