
あなたが惑星地球に十分長く住んでいるなら、空は通常青いのになぜ日没で赤面するのか疑問に思うでしょう。 これの(主な)理由となった光学現象は、 レイリー散乱と呼ばれます。 この記事では、大気散乱をシミュレートして、惑星に現れる多くの視覚効果をシミュレートする方法を説明します。 エイリアンの惑星の物理的に正確な画像をレンダリングする方法を学びたい場合、このチュートリアルは間違いなく探索する価値があります。

この記事は、次のパートに分かれています。
- パート1.大気の体積散乱
- パート2.大気散乱の理論
- パート3.レイリー散乱の数学
- パート4.大気圏を旅する
- パート5.大気シェーダー
- パート6.大気の交差点
- パート7.大気分散シェーダー
パート1.大気の体積散乱
はじめに
空は不透明な物体ではないため、大気現象を再現することは非常に困難です。 従来のレンダリング手法では、オブジェクトは単に空のシェルであると想定しています。 すべてのグラフィック計算は材料の表面で実行され、内部の内容に依存しません。 この強力な単純化により、不透明なオブジェクトを非常に効率的にレンダリングできます。 ただし、一部の材料の特性は、光がそれらを通過できるという事実によって決まります。 半透明のオブジェクトの最終的な外観は、光と内部構造の相互作用の結果です。 ほとんどの場合、チュートリアル「 Unityでの表面下散乱の高速シェーダー 」で見られるように、この相互作用は非常に効果的にシミュレートできます。 残念ながら、私たちの場合、説得力のある空を作成したい場合、これはそうではありません。 惑星の「外殻」だけをレンダリングする代わりに、大気を通過する光線がどうなるかをシミュレートする必要があります。 オブジェクト内で計算を実行することをボリュームレンダリングと呼びます 。 このトピックについては、一連のボリュームレンダリングの記事で詳しく説明しました。 この一連の記事では、大気散乱のシミュレーションに効果的に使用できない2つの手法( レイマーチングと符号距離関数 )について説明しました。 この記事では、多くの場合単位体積散乱と呼ばれる、半透明のソリッドオブジェクトのレンダリングに適した手法について学習します。
単一散乱
光のない部屋では、何も見えません。 オブジェクトは、光線が反射されて目に入るときにのみ表示されます。 ほとんどのゲームエンジン(UnityやUnrealなど)は、光が「真空」内を移動することを想定しています。 これは、オブジェクトのみが光に影響を与えることができることを意味します。 実際、光は常に環境内を移動します。 私たちの場合、そのような媒体は私たちが吸入する空気です。 したがって、空気中の光が移動する距離は、オブジェクトの外観に影響します。 地球の表面では、空気密度は比較的小さく、その影響は非常に小さいため、光が長距離を移動する場合にのみ考慮する必要があります。 遠くの山は空と合流しますが、大気散乱は近くのオブジェクトにはほとんど影響しません。
大気散乱の光学効果を再現する最初のステップは、光が空気などの媒体をどのように通過するかを分析することです。 上で述べたように、私たちは光が目に入ったときにのみオブジェクトを見ることができます。 3Dグラフィックスのコンテキストでは、私たちの目はシーンのレンダリングに使用されるカメラです。 私たちの周りの空気を構成する分子は、それらを通過する光線を反射できます。 そのため、オブジェクトの認識方法を変更できます。 大幅に簡略化すると、分子が視力に影響を与える可能性がある2つの方法があります。
外方散乱
分子が光と相互作用する最も明白な方法は、光を反射して方向を変えることです。 カメラに向けられた光線が反射される場合、 外側に散乱するプロセスを観察します。

実際の光源は1秒間に4兆個の光子を放出し、一定の確率でそれぞれが空気分子と衝突する可能性があります。 光が移動する媒体の密度が高いほど、単一光子の反射が起こりやすくなります。 外方散乱の効果は、光の移動距離にも依存します。

外方散乱は、光が徐々に薄暗くなるという事実につながり、この特性は移動距離と空気密度に依存します。
内側への散乱
光が粒子によって反射されると、カメラにリダイレクトされることがあります。 このような効果は外方散乱の反対であり、 内方散乱と呼ばれるのは論理的です。
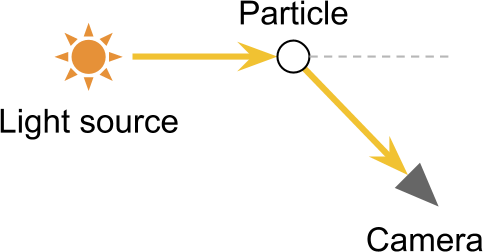
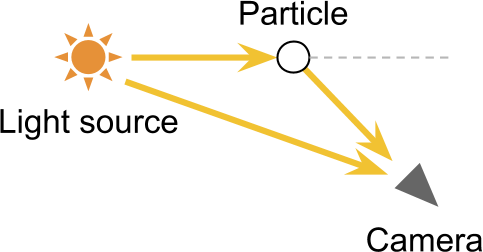
特定の条件下では、内側への散乱により、カメラの直接の視野内にない光源を見ることができます。 これの最も明らかな結果は、光学効果-光源の周りの光のハローです。 これらは、カメラが1つの光源から直接光線と間接光線の両方を受け取るという事実により発生し、事実上、受け取る光子の数が増加します。
単位体積散乱
1つの光線は、任意の回数だけ反射できます。 つまり、カメラに入る前です。 ビームは非常に難しいルートを通過できます。 高品質の半透明のマテリアルをレンダリングするには、個々の光線のそれぞれのパスをシミュレートする必要があるため、これは私たちにとって深刻な困難になります。 この手法はレイトレーシングと呼ばれ、現在、リアルタイムで実装するにはコストがかかりすぎます。 このチュートリアルで紹介するユニット散乱技術では、単一の光ビーム散乱イベントを考慮します。 後で、このような単純化により、実際のレイトレーシングに必要な計算のほんの一部で現実的な結果を得ることができることがわかります。
現実的な空をレンダリングする基礎は、惑星の大気を通過するときに光線に何が起こるかをシミュレートすることです。 下の図は、惑星を覗くカメラを示しています。 このレンダリング手法の主なアイデアは、光がどのように移動するかを計算することです A で B 散乱が影響します。 これは、カメラに入射するビームに対する散乱の影響を計算する必要があることを意味します。 上記のように、外部への散乱により、減衰が観察されます。 各ポイントに存在する光の量 P in\上線AB カメラからの反射の可能性はわずかです。
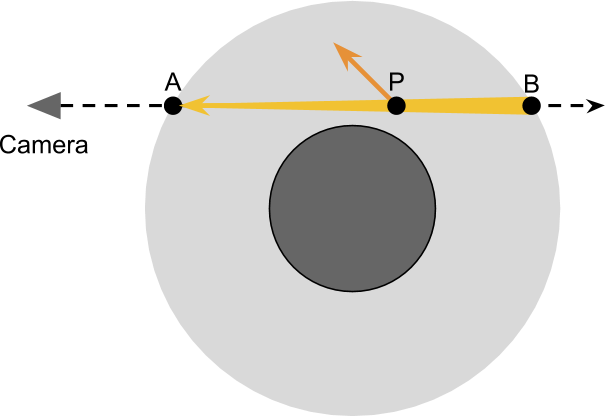
各ポイントで発生する外方散乱の量を正しく考慮する P 、最初にどのくらいの光が存在していたかを知る必要があります P 。 1つの星だけが惑星を照らしていると仮定すると、受け取ったすべての光 P 太陽から来なければなりません。 この光の一部は内側に散乱し、カメラで反射されます。
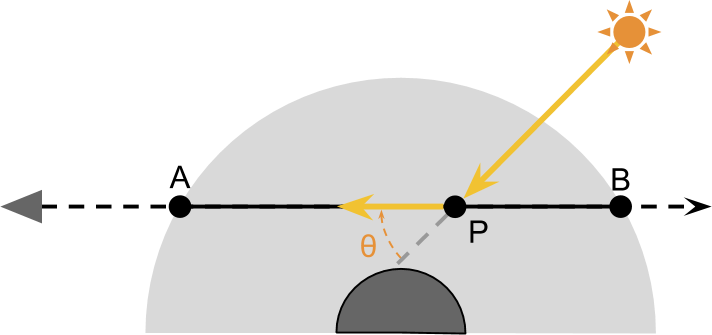
これらの2つのステップは、大気で観測されるほとんどの影響を近似するのに十分です。 ただし、光の量が P 光が大気を通過するとき、太陽からも外に散乱する C で P 。

必要なことをまとめると:
- カメラのスコープは大気中に侵入します A にあります B ;
- 近似として、各点で発生する散乱の影響を考慮します P in\上線AB ;
- 受光量 P 太陽から;
- 受光量 P 大気中を通過するときに外側に散乱する CPの上 ;
- 受けた光の一部 P 内側に散乱する傾向があり、光線をチャンバーにリダイレクトします。
- 世界の一部 P チャンバーに向けられた光は外に散乱し、視野から反射されます。
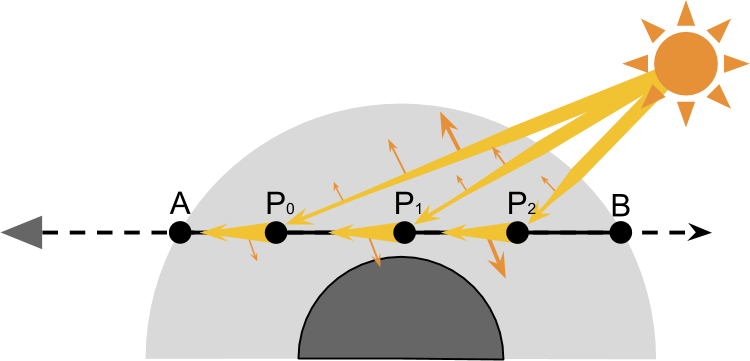
ただし、光線がカメラに入る方法は多数あります。 たとえば、途中で外側に散乱する光線の1つ P 、2回目の衝突では、カメラに向かって散乱する可能性があります(下の図を参照)。 また、3回、または4回反射した後、カメラに到達する光線がある場合があります。

検討している手法は、 単一散乱と呼ばれます。これは、視野に沿った内側への散乱のみを考慮するためです。 より洗練された技術は、このプロセスを拡張し、ビームがカメラに到達する他の方法を考慮することができます。 ただし、可能なパスの数は、指数関数的に考慮される散乱イベントの数の増加とともに増加します。 幸いなことに、カメラに入る可能性も指数関数的に減少します。
パート2.大気散乱の理論
このパートでは、この複雑で素晴らしい光学現象を支配する方程式の導出を開始します。
送信機能
カメラに送信される光の量を計算するには、太陽からの光線が通過するのと同じ旅をするのが便利です。 下の図を見ると、光線が届くのは簡単です C 空きスペースを通過します。 彼らの道には何もないので、すべての光が届きます C 散乱効果は受けません。 変数を示しましょう Ic ドットが受け取る非散乱光の量 C 太陽から。 彼の旅の間に P 、光線は惑星の大気に入ります。 いくつかの光線は、空中にぶら下がっている分子と衝突し、さまざまな方向に反射されます。 その結果、光の一部が邪魔にならないように散乱されます。 届く光の量 P (として指定 IP )より小さい Ic 。

比率 Ic そして IP パスと呼ばれる:
T\左(\上線CP\右)= fracIPIC
これを使用して、からの移動時に散乱されなかった(つまり、 見逃された )光の割合を示すことができます C 前に P 。 後で、この関数の性質を探ります。 これまでのところ、私たちが知る必要があるのは、それが外の大気散乱の効果に対応しているということだけです。
その結果、受光量 P 等しい:
IP=IC\、T\左(\上線CP\右)
散乱関数
ポイント P 太陽から直接光を受けます。 ただし、このすべての光が通過するわけではありません P カメラに送信されます。 カメラに実際に到達する光の量を計算するために、新しい概念を導入します : 散乱関数 S 。 特定の方向に反射した光の量を示します。 下の図を見ると、ある角度で反射した光線のみがカメラに向けられていることがわかります。 \シータ 。

価値 S\左(\ラムダ、\シータ、h\右) 反射する光の割合を示します \シータ ラジアン。 この関数は私たちの主な問題であり、次のパートでその性質を調べます。 これまでのところ、あなたが知る必要がある唯一のことは、それが受信した光の色に依存するということです( 波長によって決定されます) \ラムダ )、 散乱角 \シータ と高さ h ポイント P 。 大気密度は高度の関数として変化するため、高度は重要です。 また、密度は散乱光の量を決定する要因の1つです。
これで、透過する光の量を示す一般的な方程式を書くために必要なすべてのツールができました。 P に A :
IPA= boxedIP\、S left( lambda、 theta、h right)\、T left( overlinePA right)
前の定義のおかげで、拡張できます IP :
IPA= boxedIC\、T left( overlineCP right)\、S left( lambda、 theta、h right)\、T left( overlinePA\右)=
= underset textin−scattering underbraceIC\、S left( lambda、 theta、h right)、 underset textout−scattering\下括弧T\左(\上線CP\右)\、T\左(\上線PA\右)
方程式はそれ自体を物語っています:
- 光は太陽から C 空間の真空内での散乱なし;
- 光は大気中に入り、 C に P 。 このプロセスでは、一部のみ T\左(\上線CP\右) 目的地に到着します。
- 太陽からの光の一部 P カメラに反映されます。 内向きの散乱を受ける光の割合は S\左(\ラムダ、\シータ、h\右) ;
- 残りの光は P 前に A 、そしてまた一部のみ T\左(\上線PA\右) 。
数値積分
前の段落を注意深く読んだ場合、輝度がさまざまな方法で記録されていることに気付くかもしれません。 記号 IPA から送信される光の量を示します P に A 。 ただし、値は受信するすべての光を考慮していません A 。 大気散乱のこれらの単純化されたモデルでは、大気中のカメラの視野に沿った各ポイントから内側への散乱を考慮します。
受け取った光の総量 A ( Ia )、すべてのポイントの影響を合計して計算されます P in\上線AB 。 数学の観点から、セグメントで \上線AB 無限の数のポイントがあるため、それらすべてを巡回することは不可能です。 ただし、分割することはできます \上線AB 長さが短い場合 ds (下の図を参照)、それぞれの影響を要約します。
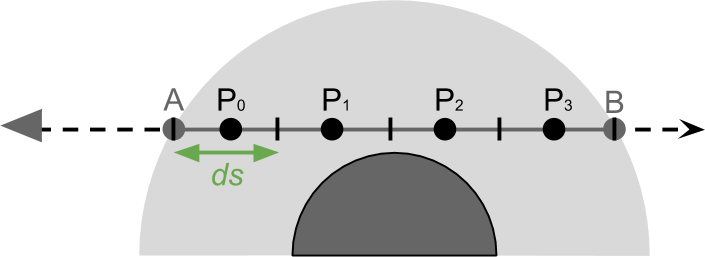
このような近似プロセスは数値積分と呼ばれ、次の式につながります。
IA= sumP in\オーバーラインABIPA\、ds
考慮に入れるポイントが多いほど、最終結果はより正確になります。 実際には、大気シェーダーでは、いくつかのポイントを単純に循環します Pi 大気の内部で、全体の結果に及ぼす影響を要約します。
別の方法で見ることができます。 ds 、すべてのポイントの影響を「平均」します。
指向性照明
太陽が比較的近い場合、 点光源としてモデル化するのが最善です。 この場合、受け取った金額 C 光は太陽までの距離に依存します。 しかし、私たちが惑星について話している場合、太陽は遠くにあるため、その光線はある角度で惑星に落ちるとしばしば思います。 これが当てはまる場合、太陽を指向性光源としてモデル化できます 。 指向性光源から受け取った光は、移動距離に関係なく一定です。 したがって、すべてのポイント C 同じ量の光を受け取り、太陽に対する方向はすべてのポイントで同じです。
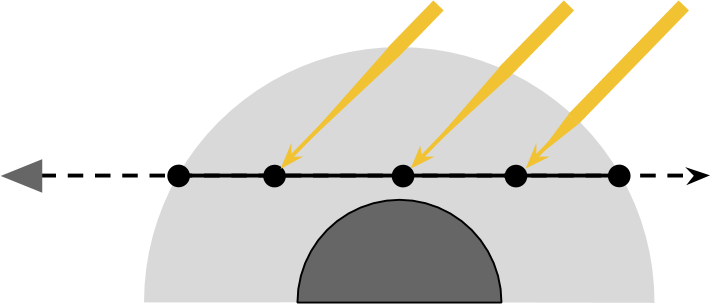
この仮定を使用して、方程式を単純化できます。
交換しましょう Ic 一定 Is 、これは太陽の明るさを決定します。
IA= sumP in\オーバーラインAB boxedIPA\、ds=
= sumP in overlineAB boxedIC\、S left( lambda、 theta、h right)\、T left( overlineCP right) 、T\左(\上線PA\右)\、ds=
=IS sumP in overlineABS left( lambda、 theta、h right)\、T left( overlineCP right)\、T left(\上線PA\右)\、ds=
実行できる別の最適化があります。これには散布関数が含まれます S\左(\ラムダ、\シータ、h\右) 。 日光が常に一方向から落ちる場合、角度 \シータ 永続的になります。 以下では、指示された影響を金額から除外できることがわかります S\左(\ラムダ、\シータ、h\右) 。 しかし、今のところ、私たちは彼を去ります。
吸収係数
光と空気分子間の相互作用の考えられる結果を説明する際に、通過または反射の2つのオプションのみを許可しました。 しかし、3番目の可能性があります。 一部の化合物は光を吸収します。 地球の大気には、この性質を持つ多くの物質があります。 たとえば、オゾンは上層大気にあり、紫外線と積極的に相互作用します。 ただし、可視スペクトル外の光を吸収するため、その存在は空の色には実質的に影響しません。 ここ地球では、光を吸収する物質の影響はしばしば無視されます。 しかし、他の惑星の場合、それを拒否することは不可能です。 たとえば、海王星と天王星の通常の着色は、大気中の大量のメタンの存在によって引き起こされます。 メタンは赤い光を吸収し、青みを帯びます。 チュートリアルの残りの部分では、吸収係数を無視しますが、大気を「色付け」する方法を追加します。
可視スペクトルの色(下)を見ると、十分な青色光が散乱している場合、空が実際に黄色または赤に変わることが簡単にわかります。

空の色は黄色いグラニュー糖の色合いに関連していると言う誘惑があります。 ただし、通常は黒に近い煙粒子が原因で、大規模な火災でも同じ効果が見られます。
パート3。レイリー散乱の数学。
このパートでは、レイリー散乱の数学、つまり空が青く見える光学現象に精通します。 方程式のこの部分で導出された方程式は、次の部分のシェーダーコードに転送されます。
はじめに
前のパートでは、シェーダーで大気散乱を近似するための優れた基礎を提供する方程式を導き出しました。 ただし、1つの式では説得力のある結果が得られないという事実を見逃しています。 美しい雰囲気のシェーダーが必要な場合は、数学を少し深くする必要があります。
光と物質の相互作用は非常に複雑であり、簡単な方法で完全に説明することはできません。 実際、大気散乱のモデリングには非常に時間がかかります。 問題の一部は、大気が均一な環境ではないことです。 その密度と組成は高さの関数として大きく異なるため、「理想的な」モデルを作成することはほとんど不可能です。
そのため、いくつかの散乱モデルが科学文献に記載されており、各モデルは特定の条件下で発生する光学現象のサブセットを説明することを目的としています。 惑星によって示された光学効果のほとんどは、 レイリー散乱と球状粒子による光散乱という 2つの異なるモデルで再現できます。 これらの2つの数学ツールを使用すると、さまざまなサイズのオブジェクトでの光散乱を予測できます。 最初のモデルでは、空気のほとんどを構成する酸素および窒素分子による光の反射をモデル化します。 後者は、花粉、ほこり、汚染物質など、下層大気に存在する大きな構造物での光の反射をモデル化します。
レイリー散乱は、青い空と赤い日没の原因です。 球形の粒子による光の散乱により、雲は白色になります。 これがどのように発生するかを知りたい場合は、散乱の数学をさらに深く掘り下げる必要があります。
レイリー散乱
粒子に衝突する光子の運命は何ですか? この質問に答えるには、より正式に言い換える必要があります。 光線が空の空間を通過して、突然粒子と衝突することを想像してください。 このような衝突の結果は、粒子のサイズと光線の色に大きく依存します。 粒子が十分に小さい場合(原子または分子のサイズ)、光の振る舞いはレイリー散乱を使用してより適切に予測されます。
何が起こっているの? 世界の一部は、影響を「感じない」旅を続けています。 ただし、この光源光のごく一部は粒子と相互作用し、すべての方向に散乱します。 ただし、すべての方向が同じ量の光を受け取るわけではありません。 光子は、粒子を直接通過するか、跳ね返る可能性が高くなります。 つまり、光子反射オプションは90度小さくなります。 この動作は、次の図で確認できます。 青い線は、散乱光の最も可能性の高い方向を示しています。

この光学現象は数学的にレイリー散乱方程式で記述されます S\左(\ラムダ、\シータ、h\右) それは私たちに光源光のシェアを与えます I0 方向に反映 \シータ :
I=I0\、S\左(\ラムダ、\シータ、h\右)
S\左(\ラムダ、\シータ、h\右)= frac pi2\左(n2−1\右)22\アンダーセット textdensity\アンダーブレース frac rho\左(h\右)N\オーバーセット textwavelength\オーバーブレース frac1 lambda4\アンダーセット\テキストジオメトリ\下括弧\左(1+ cos2\シータ\右)
どこで:
- \ラムダ :入射光の波長 ;
- \シータ : 散乱角
- h :ポイントの高度 ;
- n=1.00029 :空気の屈折率 ;
- N=2.504 cdot1025 :標準大気の立方メートルあたりの分子数。
- rho\左(h\右) : 密度係数 。海面でのこの数は 1 、および増加とともに指数関数的に減少します h 。 この関数について多くのことを言うことができます。以下の部分でそれを検討します。
このチュートリアルで使用される式は、科学記事「 大気の散乱を考慮に入れた地球の表示」 、西田他から引用されています。
空気分子から光の粒子が非常に奇妙に反射される理由を理解することにまだ興味がある場合は、何が起こっているのかを直感的に理解することで次の説明が得られます。
レイリー散乱の理由は、実際には粒子の「反発」ではありません。 光は電磁波であり、特定の分子に存在する電荷の不平衡と相互作用する可能性があります。 これらの電荷は、結果として生じる電磁放射の吸収により飽和し、後に再び放射されます。 角度関数に示された二部形状は、空気分子が微小アンテナのように放射する電気双極子になる方法を示しています。
レイリー散乱で最初に確認できることは、ある方向では他の方向よりも多くの光が伝搬することです。 2番目の重要な側面は、散乱光の量が波長に大きく依存することです。 \ラムダ 来て光。 下の円グラフはレンダリングします S\左(\ラムダ、\シータ、0\右) 3つの異なる波長用。 計算 S で h=0 しばしば海面散乱と呼ばれます 。

以下の図は、可視スペクトルの連続波長/色範囲の散乱係数の視覚化を示しています(コードはShaderToyで利用可能です)。
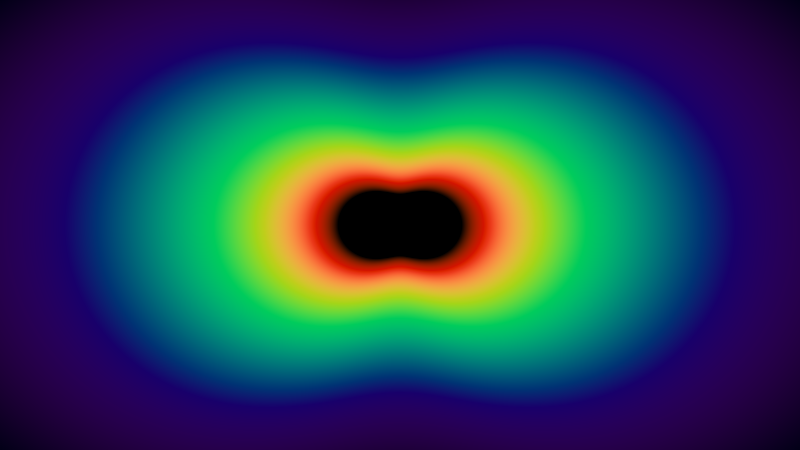
この範囲の波長は可視スペクトルの外側にあるため、画像の中心は黒く見えます。
レイリー散乱係数
レイリー散乱方程式は、特定の方向に散乱される光の量を示します。 ただし、どのくらいのエネルギーが消費されたかはわかりません。 これを計算するには、 すべての方向のエネルギー散逸を考慮する必要があります。 方程式の導出は簡単ではありません。 複雑な分析をマスターしていない場合、結果は次のとおりです。
beta left( lambda、h right)= frac8 pi3 left(n2−1 right)23 frac rho left(h right)N frac1 lambda4
どこで beta left( lambda、h right) 単一の粒子との衝突後の散乱により失われるエネルギーの割合を示します。 多くの場合、この値はレイリー散乱係数と呼ばれます。
チュートリアルの前の部分を読んだ場合、あなたはそれを推測することができます \ベータ 実際には 、透過率の決定に使用された減衰係数です T\左(\上線AB\右) セグメント上 \上線AB 。
残念ながら、計算 \ベータ とても高い。 作成するシェーダーでは、できるだけ多くの計算を保存しようとします。 このため、定数であるすべての要因を散乱係数から「抽出」すると便利です。 私たちに与えるもの \ベータ\左(\ラムダ\右) 、 海面でのレイリー散乱係数 ( h=0 ):
beta left( lambda right)= frac8 pi3 left(n2−1 right)23 frac1N frac1 lambda4
統合を試みることができます S\左(\ラムダ、\シータ、h\右) によって \シータ 間隔で \左[0.2 pi\右] しかし、それは間違いです。
レイリー散乱を2次元で視覚化したという事実にもかかわらず、これは実際には3次元の現象です。 散乱角 \シータ 3D空間で任意の方向を取ることができます。 に依存する関数の完全な分布を考慮した計算 \シータ 三次元空間で S )は立体角上の積分と呼ばれます:
beta left( lambda、h right)= int2 pi0 int pi0S left( lambda、 theta、h right) sin theta\、d thetad phi
内部積分運動 \シータ XY平面で、外側の平面は結果をX軸の周りに回転させて、3番目の次元を考慮します。 追加しました sin theta 球面角度に使用されます。
統合プロセスは、依存するもののみに関心があります \シータ 。 複数のメンバー S\左(\ラムダ、\シータ、h\右) 定数であるため、積分記号の下から転送できます。
beta left( lambda、h right)= int2 pi0 int pi0 underset textconstant underbrace frac pi2\左(n2−1\右)22 frac rho\左(h\右)N frac1 lambda4 left(1+ cos2 theta right) sin theta\、d thetad phi=
= frac pi2 left(n2−1 right)22 frac rho left(h right)N frac1 lambda4 int2 pi0 int pi0 left(1+ cos2 theta right) sin theta\、d thetad phi
これにより、内部積分が大幅に簡素化され、次の形式になります。
beta left( lambda、h right)= frac pi2 left(n2−1 right)22 frac rho left(h right)N frac1 lambda4 int2 pi0 boxed int pi0 left(1+ cos2 theta\右) sin theta\、d thetad phi=
= frac pi2 left(n2−1 right)22 frac rho left(h right)N frac1 lambda4 int2 pi0 boxed frac83d phi
これで、外部統合を実行できます。
beta left( lambda、h right)= frac pi2 left(n2−1 right)22 frac rho left(h right)N frac1 lambda4 boxed int2 pi0 frac83d phi=
= frac pi2 left(n2−1 right)22 frac rho left(h right)N frac1 lambda4 boxed frac16 pi3
これにより、最終フォームに到達します。
beta left( lambda、h right)= frac8 pi3 left(n2−1 right)23 frac rho left(h right)N frac1 lambda4
これはすべての方向の散乱の影響を考慮した積分なので、式はもはや依存していません \シータ 。
この新しい方程式は、異なる色がどのように散らばっているのかを理解する別の方法を提供します。 以下のグラフは、光がさらされる散乱の量をその波長の関数として示しています。

これは散乱係数間の強い関係です。 \ベータ そして \ラムダ これは日没時に赤い空を引き起こします。 太陽から受け取った光子は、より広い範囲の波長に分布します。 レイリー散乱は、地球の大気の原子や分子が緑や赤よりも青を強く散乱することを示しています。 光が十分に長く移動できる場合、散乱のためにその青色成分全体が失われます。 これは、日没時に光が表面とほぼ平行に移動するときに起こることです。
同じように推論すると、空が青く見える理由を理解できます。 太陽の光は一方向から落ちています。 ただし、その青色成分はすべての方向に散在しています。 空を見ると、すべての方向から青い光が当たります。
レイリー位相関数
レイリー散乱を記述する元の方程式、 S\左(\ラムダ、\シータ\右) 、2つのコンポーネントに分解できます。 最初は、導出したばかりの散乱係数です。 \ベータ\左(\ラムダ\右) その強度を変調します。 2番目の部分は散乱ジオメトリに関連し、その方向を制御します。
S left( lambda、 theta、h right)= beta left( lambda、h right) gamma left( theta right)
この新しい価値 \ガンマ\左(\シータ\右) 分割することで取得できます S\左(\ラムダ、\シータ、h\右) に \ベータ\左(\ラムダ\右) :
gamma left( theta right)= fracS left( lambda、 theta、h right) beta left( lambda right)=
= undersetS left( lambda、 theta、h right) underbrace frac pi2 left(n2−1 right)22 frac rho left(h right)N frac1 lambda4 left(1+ cos2 theta right)、 underset frac1 beta left( lambda right) underbrace frac38 pi3 left(n2−1 right)2 fracN rho\左(h\右)\ラムダ4=
= frac316 pi left(1+ cos2 theta right)
この新しい式は、入射光の波長に依存しないことがわかります。 これは、レイリー散乱が短波により強く影響することが確実にわかっているため、直感に反するように思われます。
しかし \ガンマ\左(\シータ\右) 上で見た双極子の形状をモデル化します。 会員 frac316 pi 正規化係数として機能し、すべての可能な角度にわたる積分 \シータ 要約 1 。 技術的に定式化された場合、積分は 4 pi ステラジアンが等しい 1 。
次のパートでは、これら2つのコンポーネントを分離することで、より効率的な方程式を導き出す方法を説明します。
まとめると
- レイリー散乱方程式 :方向に反射した光の割合を示します \シータ 。 散乱の量は波長によって異なります。 \ラムダ 入ってくる光。
S left( lambda、 theta、h right)= frac pi2 left(n2−1 right)22 frac rho left(h right)N frac1 lambda4 left(1+ cos2 theta right)
さらに:
S left( lambda、 theta、h right)= beta left( lambda、h right) gamma left( theta right)
- レイリー散乱係数 :最初の衝突後の散乱により失われた光の割合を示します。
beta left( lambda、h right)= frac8 pi3 left(n2−1 right)23 frac rho left(h right)N frac1 lambda4
- 海面でのレイリー散乱係数 :これはアナログです \ベータ\左(\ラムダ、0\右) 。 この追加の係数を作成すると、より効率的な方程式を導き出すのに非常に役立ちます。
beta left( lambda right)= beta left( lambda、0 right)= frac8 pi3 left(n2−1 right)23 frac1N frac1 lambda4
赤、緑、青の色にほぼ対応する波長を考慮すると、次の結果が得られます。
\ベータ\左(680nm\右)=0.00000519673
\ベータ\左(550nm\右)=0.0000121427
\ベストータ \左( 440 N M \右) = 0.0000296453
これらの結果は、次の仮定の下で計算されます。 h = 0 (これは、 r h o = 1 ) これは、分散係数が最大値をとる海面でのみ発生します。 したがって、光散乱の量の「ガイド」として機能します。
- レイリー位相関数 :散乱ジオメトリを制御します 。これは、特定の方向で失われる光の相対的な割合を示します。 係数 f r a c 3 16 p i 正規化係数として機能するため、単位球上の積分は 1 。
gamma left( theta right)= frac316 pi left(1+ cos2 theta right)
- 密度係数 :この関数は、大気の密度をシミュレートするために使用されます。 その正式な定義を以下に示します。 数学的ネタバレに反対でない場合は、次のように定義されます。
\ rho \ left(h \ right)= exp \ left \ {-\ frac {h} {H} \ right \}
どこで H=$850 メートルは高さの減少と呼ばれます。
パート4。大気中を旅します。
このパートでは、異なる高さでの大気密度のモデリングを検討します。 大気の密度はレイリー散乱の正しい計算に必要なパラメーターの1つであるため、これは必要な手順です。
大気密度係数
これまでのところ、大気密度係数の役割は考慮していません rho 。 散乱力は大気の密度に比例することは論理的です。 1立方メートルあたりの分子が多いほど、光子散乱の可能性が高くなります。 困難なのは、大気の構造が非常に複雑であり、圧力、密度、温度が異なる複数の層で構成されていることです。 幸いなことに、レイリー散乱の大部分は大気の最初の60 kmで発生します。 対流圏では、温度は直線的に低下し、圧力は指数関数的に低下します。
下の図は、下層大気の密度と高さの関係を示しています。
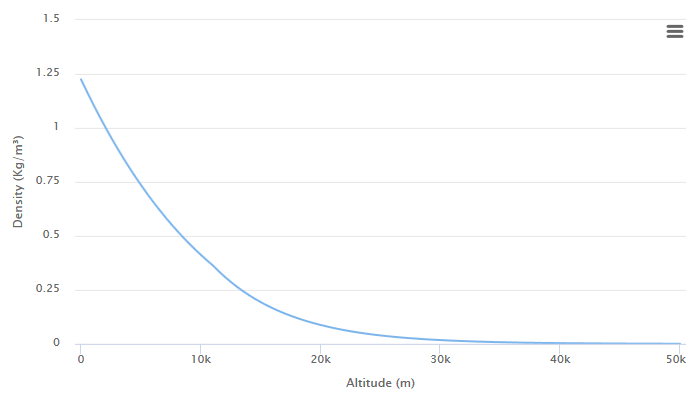
価値 rho\左(h\右) 高度での大気の測定値です h ゼロから始まる方法で正規化されたメートル。 多くの科学記事で rho 次のように定義することもできるため、密度係数とも呼ばれます。
rho left(h right)= fracdensity left(h right)density left(0 right)
真の密度を 密度\左(0\右) 私たちはそれを得る rho\左(h\右) 海面で等しい 1 。 ただし、上記で強調したように、計算 密度\左(h\右) 些細なことからほど遠い。 これを指数曲線として近似できます。 あなた方の何人かは、低気圧の密度が指数関数的に減少していることに既に気付いているかもしれません。
密度曲線を指数曲線で近似したい場合は、次のようにします。
\ rho \ left(h \ right)= exp \ left \ {-\ frac {h} {H} \ right \}
どこで H0 縮小高さと呼ばれるスケール係数です。 地球の低層大気におけるレイリー散乱については、しばしば H=$850 メートル(下図を参照)。 球状粒子による光の散乱の場合、多くの場合、値はほぼ等しい 1200 メートル。
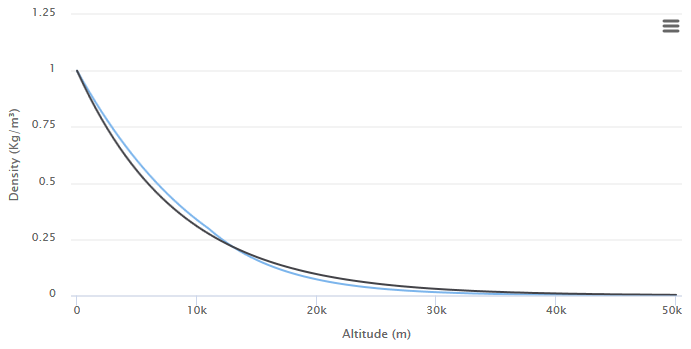
に使用される値 H 最良の近似を与えない rho\左(h\右) 。 ただし、これは実際には問題ではありません。 このチュートリアルで提示される値のほとんどは、深刻な近似を受けています。 視覚的に快適な結果を作成するには、参照画像に使用可能なパラメーターを調整する方がはるかに効率的です。
指数関数的な減少
チュートリアルの前の部分で、個々の粒子と相互作用した後に光線がさらされる外方散乱を考慮する方法を示す方程式を思いつきました。 この現象をモデル化するために使用される値は、散乱係数と呼ばれていました。 \ベータ 。 それを考慮するために、係数を導入しました \ベータ 。
レイリー散乱の場合、1回の相互作用で大気散乱の影響を受ける光の量を計算するための閉形式も導出しました。
beta left( lambda、h right)= frac8 pi3 left(n2−1 right)23 frac rho left(h right)N frac1 lambda4
海面で計算するとき、つまり h=0 、方程式は次の結果を与えます:
\ベータ\左(680nm\右)=0.00000519673
\ベータ\左(550nm\右)=0.0000121427
\ベータ\左(440nm\右)=0.0000296453
どこで 680 、 550 そして 440 -赤、緑、青にほぼ対応する波長。
これらの数字の意味は何ですか? それらは、粒子との単一の相互作用で失われる光の割合を表します。 光線が最初に明るさを持っていると仮定して I0 (一般的な)散乱係数で大気の一部を通過させます \ベータ 、その後、散乱後に残る光の量は次のとおりです。
I1=I0⏟initial energy−I0β⏟energy lost=I0(1−β)
これは1回の衝突の場合に当てはまりますが、特定の距離内でどのようなエネルギーが消費されるかについて関心があります。これは、残りの光がすべての点でこのプロセスを経ることを意味します。
光が散乱係数を持つ均一な媒体を通過するとき\ベータ、特定の距離を移動したときにどれだけ残るかをどのように計算できますか?
分析を学んだ人にとっては、これはおなじみのように思えるかもしれません。連続的なセグメントで乗算プロセスが繰り返される場合(1−β)、次にオイラー数がシーンに入ります。通過後の散乱後に残っている光の量x メートルが等しい:
I=I0exp{−βx}
繰り返しますが、指数関数に直面しています。密度係数を表す指数関数とは関係ありません。ρ 。どちらの現象も指数関数的であるため、両方の現象は指数関数で記述されます。それ以外は、それらの間に関係はありません。
. , , :
I 1 = I 0 ( 1 - β2)
I 2 = I 1( 1 - β2)
:
I 2 = I 0 ( 1 - β2)(1−β2)=
=I0(1−β2)2
I2 . ? ? ? :
I=limn→∞I0(1−βn)n
どこで limn→∞ — , . , ∞ , - β∞ 。
:
limn→∞(1−βN)N=E-β=EXP{-β}
, .
均一な透過率
チュートリアルの後半では、伝送の概念を紹介しました T散乱プロセス後に大気を通過するときに残る光の割合として。これで、それを記述する方程式を推定するためのすべての要素ができました。
下の図を見て、セグメントの透過率を計算する方法を考えてみましょう CPの上 。 光線が届くことが簡単にわかります C空のスペースを通過します。したがって、それらは散らばっていません。その結果、C実際に太陽の明るさに等しい IS 。 この旅の間に P光の一部は邪魔にならないように散乱されます。したがって、到達する光の量P ( IP )より小さい IS 。

散乱光の量は、移動距離によって異なります。パスが長いほど、減衰が大きくなります。指数関数的減少の法則によれば、ある点での光量IP 次のように計算できます。
IP=ISexp{−β¯CP}
どこで CPの上 -セグメントの長さ C 前に P 、そして exp{x}- 指数関数 ex 。
大気伝送
反射の確率(散乱係数 \ベータ に沿って各点で同じ CPの上 。 残念ながら、そうではありません。
散乱係数は、大気の密度に大きく依存します。立方メートルあたりの空気分子が多いほど、衝突の可能性が高くなります。惑星の大気の密度は不均一であり、高度によって異なります。これはまた、外向き散乱を計算できないことを意味します CPの上ワンステップで。この問題を解決するには、散乱係数を使用して各ポイントで外向きの分散を計算する必要があります。
これがどのように機能するかを理解するために、近似から始めましょう。線分 CPの上 2つに分かれています ¯CQ そして ¯QP 。

まず、光の量を計算します C 到達する Q :
IQ=ISexp{−β(λ,h0)¯CQ}
次に、同じアプローチを使用して、到達する光の量を計算します P から Q :
IP=IQexp{−β(λ,h1)¯QP}
代用すれば IQ 2番目の方程式に入れて単純化すると、

もし ¯CQ そして ¯QP 同じ長さを持っている ds 、式をさらに簡略化できます。
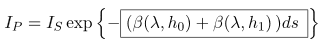
異なる散乱係数を持つ同じ長さの2つのセグメントの場合、外向きの散乱は、個々のセグメントの散乱係数を合計し、セグメントの長さを掛けることによって計算されます。
任意の数のセグメントでこのプロセスを繰り返し、真の値にますます近づいていきます。これにより、次の方程式が導かれます。
IP=ISexp{−∑Q∈¯CPβ(λ,hQ)ds}
どこで hQ -ポイントの高さ Q 。
先ほど使用した直線を多くのセグメントに分割する方法は、数値積分と呼ばれます。
最初に受け取った光の量が1 、任意のセグメントを通る大気透過の方程式を取得します。
T(¯CP)=exp{−∑Q∈¯CPβ(λ,hQ)ds}
この式をさらに拡張できます。合計を置き換える\ベータ レイリー散乱で使用される実際の値、 \ベータ :
T(¯CP)=exp{−∑Q∈¯CP8π3(n2−1)23ρ(hQ)N1λ4ds}
多くの要因 \ベータ 以下の量で実行できるように、定数
T(¯CP)=exp{−8π3(n2−1)231N1λ4⏟constantβ(λ)optical depthD(¯CP)⏞∑Q∈¯CPρ(hQ)ds}
合計で表される値は、光学的厚さと呼ばれます D(¯CP)これをシェーダーで計算します。残りは、一度しか計算できない倍率であり、海面での散乱係数に対応します。完成したシェーダーでは、海面での光学的厚さと散乱係数のみを計算します\ベータ入力として送信します。
要約すると:
T(¯CP)=exp{−β(λ)D(¯CP)}
パート5.大気シェーダー。
はじめに
シェーダーを書く
このエフェクトのシェーダーの作成を無数の方法で開始できます。大気散乱を惑星にレンダリングしたいので、球体で使用されると仮定するのは論理的です。
このチュートリアルを使用してゲームを作成する場合、既存の惑星にシェーダーを適用する可能性があります。スウォッチの上に大気散乱計算を追加することは可能ですが、通常は結果が良くありません。その理由は、大気が惑星の半径よりも大きいため、わずかに大きいサイズの透明な球体にレンダリングする必要があるためです。下の図は、大気が惑星の表面上に広がり、背後の空の空間と混ざり合っている様子を示しています。

別の球体への分散性材料の適用は可能ですが、冗長です。このチュートリアルでは、大気をわずかに大きな球体にレンダリングするシェーダーパッセージを追加して、Standard Surface Shader Unityを拡張することをお勧めします。これを大気圏と呼びます。
2パスシェーダー
Unity サーフェスシェーダーを使用していた場合、 頂点およびフラグメント シェーダーで複数のパスが設定される
Pass
ブロックをサポートしていないことに気付くかもしれません。
2つのパスでシェーダーを作成することができます
SubShader
コードの2つの個別のセクションを1つの
SubShader
ブロックに追加するだけです。
Shader "Custom/NewSurfaceShader" { Properties { _Color ("Color", Color) = (1,1,1,1) _MainTex ("Albedo (RGB)", 2D) = "white" {} _Glossiness ("Smoothness", Range(0,1)) = 0.5 _Metallic ("Metallic", Range(0,1)) = 0.0 } SubShader { // --- --- Tags { "RenderType"="Opaque" } LOD 200 CGPROGRAM // Cg ENDCG // ------------------ // --- --- Tags { "RenderType"="Opaque" } LOD 200 CGPROGRAM // Cg ENDCG // ------------------- } FallBack "Diffuse" }
最初のパスを変更して、惑星をレンダリングできます。 これからは、2回目のパスに焦点を当て、大気中の散乱を実現します。
通常の押し出し
大気圏は惑星よりわずかに大きい。 これは、2番目の通路が球体を押し出すことを意味します。 モデルが滑らかな法線を使用している場合、法線の押し出しと呼ばれる手法を使用してこの効果を実現できます。
通常の押し出しは、最も古いシェーダートリックの1つであり、通常、最初に調査されるものの1つです。 私のブログには多くの参照があります。 良い出発点は、 「 シェーダー 入門」シリーズのSurface Shaderの投稿でしょう。
法線の押し出しの仕組みに慣れていない場合は、説明します。すべての頂点は、 頂点関数を使用してシェーダーによって処理されます 。 この関数を使用して各頂点の位置を変更し、球体を大きくすることができます。
最初のステップは、
vertex:vert
を追加して
pragma
ディレクティブを変更することです
vertex:vert
; これにより、Unityは各頂点に対して
vert
関数を実行します。
#pragma surface surf StandardScattering vertex:vert void vert (inout appdata_full v, out Input o) { UNITY_INITIALIZE_OUTPUT(Input,o); v.vertex.xyz += v.normal * (_AtmosphereRadius - _PlanetRadius); }
このコードフラグメントは、法線に沿って球を押し出す頂点関数を示しています。 球の押し出し速度は、大気のサイズと惑星のサイズに依存します。 これらの値は両方とも、 マテリアルインスペクターからアクセスできるプロパティとしてシェーダーに渡す必要があります。
シェーダーは、惑星の中心がどこにあるかを知る必要もあります。 頂点関数にも計算を追加できます。 記事「 頂点とフラグメントシェーダー 」で説明した世界の空間でオブジェクトの中心点を見つける。
struct Input { float2 uv_MainTex; float3 worldPos; // Unity float3 centre; // }; void vert (inout appdata_full v, out Input o) { UNITY_INITIALIZE_OUTPUT(Input,o); v.vertex.xyz += v.normal * (_AtmosphereRadius - _PlanetRadius); o.centre = mul(unity_ObjectToWorld, half4(0,0,0,1)); }
UNITY_INITIALIZE_OUTPUT
が含まれていることが
UNITY_INITIALIZE_OUTPUT
ます。 シェーダーはオブジェクトの空間内の頂点の位置を取得し、Unityが提供する位置、スケール、回転を使用して、ワールドの座標にそれらを投影する必要があります。
そして、これは
UNITY_INITIALIZE_OUTPUT
によって実行される操作の1つです。 それがなければ、これらの計算に必要なコードを自分で記述する必要があります。
添加剤ブレンド
対処する必要があるもう1つの興味深い機能は、透明性です。 通常、透明な素材を使用すると、オブジェクトの背後にあるものを確認できます。 私たちの場合、この解決策は機能しません。大気は単なる透明なプラスチックではないからです。 光が通過するため、加算混合モードを使用して惑星の光度を上げる必要があります 。
標準のUnity Surface Shaderでは、デフォルトでブレンドモードは有効になっていません。 状況を変更するには、2番目のパスのラベルを次のものに置き換える必要があります。
Tags { "RenderType"="Transparent" "Queue"="Transparent"} LOD 200 Cull Back Blend One One
Blend One One
エクスプレッションはシェーダーによって使用され、加算ブレンディングモードにアクセスします。
ネイティブ照明機能
ほとんどの場合、サーフェスシェーダーを記述するとき、プログラマはその
surf
関数を変更します。これは、アルベド、表面の滑らかさ、金属特性などの「物理的な」特性を提供するために使用されます。 これらのプロパティはすべて、シェーダーによってリアルなシェーディングを計算するために使用されます。
私たちの場合、これらの計算は必要ありません。 それらを取り除くには 、シェーダーで使用されている照明モデルを削除する必要があります。 このトピックを詳細に調べました。 次の投稿を調べて、これを行う方法を理解できます。
- 3Dプリンターシェーダー効果 (Habréでの翻訳 )
- CD-ROMシェーダー:回折格子
- Unityでの高速表面下散乱 (Habré 翻訳 )
新しい照明モデルは
StandardScattering
と呼ばれます。 リアルタイム照明とグローバル照明用の関数、つまり
LightingStandardScattering
と
LightingStandardScattering_GI
をそれぞれ作成する必要があります。
記述する必要があるコードは、照明の方向やビューの方向などのプロパティも使用します。 これらは、次のコードスニペットを使用して取得できます。
#pragma surface surf StandardScattering vertex:vert #include "UnityPBSLighting.cginc" inline fixed4 LightingStandardScattering(SurfaceOutputStandard s, fixed3 viewDir, UnityGI gi) { float3 L = gi.light.dir; float3 V = viewDir; float3 N = s.Normal; float3 S = L; // float3 D = -V; // , ... } void LightingStandardScattering_GI(SurfaceOutputStandard s, UnityGIInput data, inout UnityGI gi) { LightingStandard_GI(s, data, gi); }
In
...
には、この効果を実装するために必要なシェーダーコード自体が含まれます。
浮動小数点精度
このチュートリアルでは、すべての計算がメートル単位で実行されると仮定します。 これは、地球をシミュレートする必要がある場合、半径6371000メートルの球体が必要であることを意味します。 実際、Unityでは、非常に大きな数と非常に小さな数を同時に処理する必要がある場合に発生する浮動小数点エラーのため、これは不可能です。
これらの制限を回避するために、散乱係数を調整して補正できます。 たとえば、惑星の半径がわずか6.371メートルの場合、散乱係数は
\ベータ\左(\ラムダ\右) 1,000,000回を超える必要があります。 H -1,000,000倍少ない。
私のUnityプロジェクトでは、すべてのプロパティと計算はメートルで表されます。 これにより、散乱係数と減少した高さに実際の物理値を使用できます。 ただし、シェーダーは球のサイズをメートル単位で取得するため、Unityユニットから実際のメートルまでスケールできます。
パート6。大気の交差点。
前述のように、大気を通過するセグメントの光学的厚さを計算する唯一の方法は、 数値積分によるものです。 これは、間隔をより短い長さに分割する必要があることを意味します ds 密度定数を考慮して、それぞれの光学的厚さを計算します。

上記は光学的厚さです。 \上線AB これは4つのサンプルで計算され、各サンプルではセグメント自体の中心の密度が考慮されます。
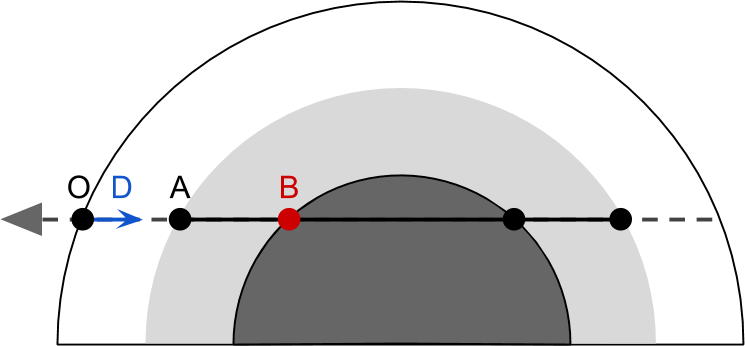
最初のステップは明らかにポイントを見つけることです A そして B 。 レンダリングするオブジェクトが球体であると仮定すると、Unityはその表面をレンダリングしようとします。 画面上の各ピクセルは、球上の点に対応しています。 以下の図では、このポイントは O ( 起源から)。 サーフェスシェーダー内 O
Input
構造の
worldPos
変数と一致します。 これは、シェーダーが行う作業量です。 私たちが利用できる唯一の情報は O 方向 D 、これは視線の方向を示し、大気圏は中心にあります C および半径 R 。 困難はコンピューティングにあります A そして B 。 ジオメトリが最速で使用され、 大気圏球とカメラの可視光線の交差点を見つける問題が軽減されます。
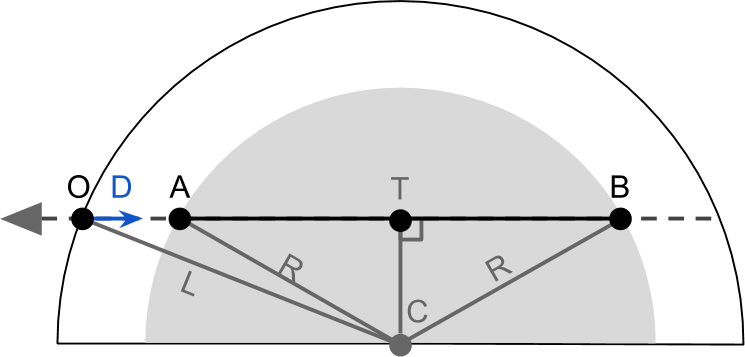
まず、それは注目に値する O 、 A そして B 視線上にあります。 これは、それらの位置を3D空間の点としてではなく、視線から原点までの距離として扱うことができることを意味します。 A 実際のポイント(シェーダーでは
float3
として
float3
)であり、 Ao -開始点までの距離 O (
float
として保存され
float
)。 A そして Ao -同じポイントを指定する2つの等しく正しい方法、つまり、それは真実です。
A=O+\上線AO\、D
B=O+\上線BO\、D
上にバーのあるエントリはどこですか XY$の上 任意の2点間のセグメントの長さを示します X そして Y 。
効率化のためのシェーダーコードでは、 Ao そして Bo 、それらを計算します Ot :
\上線AO=\上線OT−\上線AT
\上線BO=\上線OT+\上線BT
また、セグメントが \上線AT そして BT$に上線を引きま 同じ長さです。 次に、交点を見つけるために、計算する必要があります \上線AO そして \上線AT 。
線分 \上線OT 計算する最も簡単な方法。 上の図を見ると、次のことがわかります。 \上線OT ベクトルの投影 CO 視線上。 数学的には、この投影はスカラー積を使用して実行できます。 シェーダーに精通している場合は、スカラー積が2つの方向の「整列」の尺度であることを知っているかもしれません。 それが2つのベクトルに適用され、そのうちの1つが単位長を持つ場合、それは射影演算子になります。
\上線OT=\左(C−O\右) cdotD
それはまた注目に値する
\左(C−O\右) 間のセグメントの長さではなく、3次元ベクトルです C そして O 。
次に、セグメントの長さを計算する必要があります \上線AT 。 三角形のピタゴン定理を使用して計算できます \オーバーセット\トライアングルACT 。 彼女は次のように主張しています:
R2=\オーバーラインAT2+\オーバーラインCT
そしてそれはそれを意味します:
overlineAT= sqrtR2− overlineCT
長さ CT$の上 まだ不明です。 ただし、ピタゴラスの定理を三角形に再度適用することで計算できます \オーバーセット\トライアングルOCT :
\上線CO2=\上線OT2+\上線CT2
\上線CT= sqrt\上線CO2−\上線OT2
これで、必要な数量がすべて揃いました。 要約すると:
\上線OT=\左(C−O\右) cdotD
\上線CT= sqrt\上線CO2−\上線OT2
\上線AT= sqrtR2−\上線CT2
\上線AO=\上線OT−\上線AT
\オーバーラインBO=\オーバーラインOT+\オーバーラインAT
この方程式のセットには平方根があります。 これらは、負でない数に対してのみ定義されます。 もし R2>\上線CT2 、解決策はありません。これは、視線が球体と交差しないことを意味します。
これを次のCg関数に変換できます。
bool rayIntersect ( // Ray float3 O, // Origin float3 D, // // float3 C, // float R, // out float AO, // out float BO // ) { float3 L = C - O; float DT = dot (L, D); float R2 = R * R; float CT2 = dot(L,L) - DT*DT; // if (CT2 > R2) return false; float AT = sqrt(R2 - CT2); float BT = AT; AO = DT - AT; BO = DT + BT; return true; }
1つではなく3つの値を返します \上線AO 、 BO$の上 交差点のバイナリ値。 これらの2つのセグメントの長さはoutキーワードを使用して返され、関数がこれらのパラメーターに加えた変更を完了した後に保存されます。
惑星との衝突
考慮すべき別の問題があります。 いくつかの可視光線が惑星と衝突するため、大気圏を通る彼らの旅は早く終わります。 1つの解決策は、上記を確認することです。
より単純ですが効率の悪いアプローチは、
rayIntersect
2回実行し、必要に応じてエンドポイントを変更することです。
これは、次のコードに変換されます。
// float tA; // (worldPos + V * tA) float tB; // (worldPos + V * tB) if (!rayIntersect(O, D, _PlanetCentre, _AtmosphereRadius, tA, tB)) return fixed4(0,0,0,0); // // ? float pA, pB; if (rayIntersect(O, D, _PlanetCentre, _PlanetRadius, pA, pB)) tB = pA;
パート7.大気分散シェーダー。
このパートでは、最終的に、惑星の大気中のレイリー散乱のシミュレーションに関する作業を完了します。

可視ビームサンプリング
最近導出した大気散乱の方程式を思い出してみましょう。
I=IS sumP in overlineABS left( lambda、 theta、h right)T left( overlineCP right)T left( overlinePA\右)ds
私たちが受け取る光の量は、太陽が発する光の量に等しく、 Is 各ポイントの個々の効果の合計で乗算 P セグメント上 \上線AB 。
この関数をシェーダーに直接実装できます。 ただし、ここでいくつかの最適化を行う必要があります。 前の部分で、式をさらに簡略化できると述べました。 最初に行うことは、散乱関数を2つの主要なコンポーネントに分割することです。
S left( lambda、 theta、h right)= beta left( lambda、h right) gamma left( theta right)= beta left( lambda right) rho left(h right) gamma left( theta right)
位相関数 \ガンマ\左(\シータ\右) および海面分散係数 \ベータ\左(\ラムダ\右) 角度に対して \シータ と波長 \ラムダ サンプリングされたポイントから独立しています。 したがって、それらは次の量で実行できます。
I=IS\、 beta left( lambda right) gamma left( theta right) sumP in overlineABT left( overlineCP right)T\左(\上線PA\右) rho\左(h\右)ds
この新しい式は、前の式と数学的に似ていますが、最も「重い」部分が合計から導出されるため、計算がより効率的です。
まだ実装の準備ができていません。 無限の数のポイントがあります P 考慮しなければなりません。 合理的な近似 I 分割されます \上線AB いくつかの短いセグメントに ds 各セグメントの影響の追加。 そうすることで、各セグメントが一定の密度を持つのに十分小さいと仮定できます。 一般的に、これはそうではありませんが、 ds 十分に小さい場合、かなり良い近似を達成できます。

のセグメント数 \上線AB すべてのセグメントが視線上にあるため、可視性のサンプルを呼び出します。 シェーダーでは、これは
_ViewSamples
プロパティになります。 これはプロパティであるため、マテリアルインスペクターからアクセスできます。 これにより、シェーダーのパフォーマンスの精度を下げることができます。
次のコードフラグメントを使用すると、大気中のすべてのセグメントをバイパスできます。
// // P AB float3 totalViewSamples = 0; float time = tA; float ds = (tB-tA) / (float)(_ViewSamples); for (int i = 0; i < _ViewSamples; i ++) { // // ( ) float3 P = O + D * (time + ds * 0.5); // T(CP) * T(PA) * ρ(h) * ds totalViewSamples += viewSampling(P, ds); time += ds; } // I = I_S * β(λ) * γ(θ) * totalViewSamples float3 I = _SunIntensity * _ScatteringCoefficient * phase * totalViewSamples;
time
変数は、開始点からの距離を追跡するために使用されます。 O 。 各反復後、
ds
だけ増加します。
光学的厚さPA
視線上のすべてのポイント \上線AB 描画するピクセルの最終色に貢献します。 数学的に表現されるこの寄与は、合計内の値です。
I=IS\、 beta left( lambda right) gamma left( theta right) sumP in overlineAB underset textlightcontributionof\、L\左(P\右)\下括弧T\左(\上線CP\右)T\左(\上線PA\右) rho\左(h\右)ds
最後の段落のように、この式を単純化してみましょう。 上記の式をさらに展開すると、 T その定義:
T \左(\上線{XY} \右)= \ exp \左\ {-\ beta \左(\ラムダ\右)D \左(\上線{XY} \右)\右\}
スキップした結果 CPの上 そして \上線PA になります:
T\左(\上線CP\右)T\左(\上線PA\右)=
= \ underset {T \ left(\ overline {CP} \ right)} {\ underbrace {\ exp \ left \ {-\ beta \ left(\ lambda \ right)D \ left(\ overline {CP} \ right )\ right \}}} \、\ underset {T \ left(\ overline {PA} \ right)} {\ underbrace {\ exp \ left \ {-\ beta \ left(\ lambda \ right)D \ left( \上線{PA} \右)\右\}}} =
= \ exp \ left \ {-\ beta \ left(\ lambda \ right)\ left(D \ left(\ overline {CP} \ right)+ D \ left(\ overline {PA} \ right)\ right) \右\}
結合された透過は指数関数的な減少としてモデル化され、その係数は光が移動する経路に沿った光学的厚さの合計です( CPの上 そして \上線PA ) 海面レベルでの分散係数 ( \ベータ で h=0 )
計算を開始する最初の値は、セグメントの光学的厚さです \上線PA 、大気圏への進入地点から現在forループでサンプリングしている地点に移動します。 光学的厚さの定義を思い出しましょう:
D \左(\上線{PA} \右)= \ sum_ {Q \ in \上線{PA}} {\ exp \左\ {-\ frac {h_Q} {H} \右\}} \、ds
「額」を実装する必要がある場合は、ループ内のポイントをループでサンプリングする
opticalDepth
関数を作成します P そして A 。 可能ですが、非常に非効率的です。 実際、 D\左(\上線PA\右) すでに最外側のforループで分析しているラインセグメントの光学的厚さです。 中心にある現在のセグメントの光学的厚さを計算すれば、多くの計算を保存できます P (
opticalDepthSegment
)、およびforループ(
opticalDepthPA
)に要約し続けます。
// float opticalDepthPA = 0; // // P AB float time = tA; float ds = (tB-tA) / (float)(_ViewSamples); for (int i = 0; i < _ViewSamples; i ++) { // // ( ) float3 P = O + D * (time + viewSampleSize*0.5); // // ρ(h) * ds float height = distance(C, P) - _PlanetRadius; float opticalDepthSegment = exp(-height / _ScaleHeight) * ds; // // D(PA) opticalDepthPA += opticalDepthSegment; ... time += ds; }
光サンプリング
光の影響の表現に戻ると P 、必要な値はセグメントの光学的厚さだけです CPの上 、
L \左(P \右)= \アンダーセット{\テキスト{複合透過率}} {\アンダーブレース{\ exp \左\ {-\ベータ\左(\ラムダ\右)\左(D \左(\オーバーライン{CP} \右)+ D \左(\上線{PA} \右)\右)\右\}}} \、\アンダーセット{\ text {optical depth of} \、ds} {\アンダーブレース{\ rho \左(h \右)ds}}
セグメントの光学的厚さを計算するコードを移動します CPの上
lightSampling
と呼ばれる
lightSampling
。 名前は、 光線から取られます。 光線は、 P 太陽に向かっています。 大気圏外に出るポイントを呼び出しました C 。
ただし、
lightSampling
関数
lightSampling
光学的厚さを計算するだけで
lightSampling
ん CPの上 。 これまでのところ、大気の影響のみを考慮し、惑星自体の役割を無視しました。 私たちの方程式は、光線がから移動する可能性を考慮していません P 太陽に、惑星と衝突するかもしれません。 この場合、光は実際にはカメラに到達しないため、この時点までに実行されたすべての計算は適用されません。
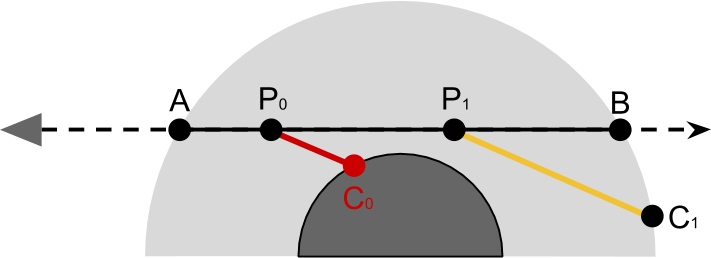
下の図では、光の影響がわかりやすい P0 太陽の光が届かないので無視する必要があります P0 。 間のポイントを循環するとき P そして C
lightSampling
は、惑星との衝突もチェックします。 これは、ネガティブ性のポイントの高さをチェックすることで実行できます。
bool lightSampling ( float3 P, // float3 S, // out float opticalDepthCA ) { float _; // float C; rayInstersect(P, S, _PlanetCentre, _AtmosphereRadius, _, C); // PC float time = 0; float ds = distance(P, P + S * C) / (float)(_LightSamples); for (int i = 0; i < _LightSamples; i ++) { float3 Q = P + S * (time + lightSampleSize*0.5); float height = distance(_PlanetCentre, Q) - _PlanetRadius; // if (height < 0) return false; // opticalDepthCA += exp(-height / _RayScaleHeight) * ds; time += ds; } return true; }
上記の関数は、最初にポイントを計算します Cの助けを借りて
rayInstersect
。次に、彼女はセグメントを分割します¯PAセグメントに
_LightSamples
長さの
ds
。光学的厚さの計算は、最も外側のループで使用されるものと同じです。
この関数は、惑星との衝突が発生した場合にfalseを返します。これを使用して、を置き換えることにより、最も外側のループの欠落コードを更新できます
...
。
// D(CP) float opticalDepthCP = 0; bool overground = lightSampling(P, S); if (overground) { // // T(CP) * T(PA) = T(CPA) = exp{ -β(λ) [D(CP) + D(PA)]} float transmittance = exp ( -_ScatteringCoefficient * (opticalDepthCP + opticalDepthPA) ); // // T(CPA) * ρ(h) * ds totalViewSamples += transmittance * opticalDepthSegment; }
すべての要素を考慮したので、シェーダーの準備ができました。
[注 レーン:著者のPatreonページで、完成したシェーダーのStandardおよびPremiumバージョンへのアクセスを購入できます。]