メソッドの開発に進む前に、プロセスで使用する主なアプローチを定義します:確率変数の生成、確率分布、および確率論と数学統計のいくつかの要素。 実験の結果では、確率分布の振る舞いの実験的なデモンストレーションとランダムなプロセスのシミュレーションが見られます。 これはすべて、確率分布が表示されるさまざまなシミュレーションモデルを作成するための手段の基礎となります。
この調査のすべてのモデリング手法は、プログラミング言語Pythonで提示されます。 この言語は、研究と教育の一般的なツールです。
今後の記事で紹介する研究のさらなる段階では、より複雑な実験に進みます:この記事の範囲に含まれていない確率分布を検討し、キューイングシステムとネットワークのシミュレーションモデリングを検討し、並列コンピューティングを使用してそのようなモデルのプログラミングを実証します。
Pythonの乱数モデリング手法と乱数ジェネレーター
1つ以上のサイコロを投げる単純なモデルを検討してください。 乱数を生成してシミュレーションを開始します。 真および準ランダム性に関する数値と質問を生成するタスクは、私たちの研究には含まれていませんが、これらの議論は他のソースで見つけることができます。 私たちのモデルは、Pythonの擬似ランダム変数ジェネレーターを使用します。 初期段階では、調査を明確にするために、シミュレーション結果を観察してテストの数を増やすことができます。
ランダム変数を生成することから始めましょう。 それらを生成する方法は、標準のPythonライブラリを使用することに要約されます。
標準ライブラリのランダムモジュールは、0〜1の範囲のランダムな実数、特定の範囲のランダムな整数、シーケンス要素のランダムな選択などを取得する機能を提供します。
ランダムモジュールは、たとえば、ゲームでカードのデッキを混合したり、スライドショープログラムや統計モデリングプログラムで画像をランダムに選択したりするために使用できます。 詳細については、Python標準ライブラリガイドを参照してください。
コンパイルおよび最適化された拡張ライブラリとPython言語NumPyを組み合わせることにより、Pythonの数学計算の実装を含むNumPy拡張機能は、Pythonを強力で効率的で便利な数学計算ツールに変えます。
NumPyモジュールの詳細な説明は、このパッケージの公式ドキュメントに記載されています。
Pythonを使用して確率分布をモデル化する方法
モデリングを始めましょう:サイコロを投げます。 以下は、1つのダイのトスのモデルのプログラミングのリストです(図1)。 キューブは、6つの値のいずれかを取ることができます。
import pylab import numpy # trials = 500 # values = numpy.random.randint(1, 7, size=trials) pylab.hist(values, bins=[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5], edgecolor='white') pylab.xlabel('') pylab.ylabel(' ') pylab.title(' ' + str(trials) + ' ') pylab.show()
図1 トスのモデルをプログラミングするためのリスト
提示されたプログラムでは、テストの数を設定します:ダイが投げられる回数と配列:各テストで落ちる値。 結果はヒストグラムとして表示されます(図2)。
結果を考慮すると、分布が均一であると仮定できます。 テストの回数を10,000回に増やすと、ヒストグラムが均一な分布のヒストグラムに似た形状を持っていることがわかります。
次のテストでは、2つのサイコロを投げるモデルを検討します。 プログラムのコードはわずかに変更されます(図3)。

図2。 1つのダイロールのシミュレーション結果
... # values = [] for i in range(trials): values.append(numpy.random.randint(1, 7) + numpy.random.randint(1, 7)) pylab.hist(values, bins=[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5, 10.5, 11.5, 12.5, 13.5], facecolor='green', edgecolor='white') ...
図3 2ダイトスモデルをプログラミングするための修正リストの一部
提示されたリストでの重要な変更は、2つのキューブのドロップされた値を書き込む配列への値の割り当てです。 それほど重要ではない2番目の変更は、対応する値オプションのヒストグラム表示です。 プログラムの結果を図4に示します。
2つの立方体のトスのシミュレーション結果を受け取ったので、正規(ガウス)分布のモデリングの問題と、それがいくつかの立方体のトスのモデリングの問題とどの程度相関するかを考えます。 プログラムコードもわずかに変更されます。配列に値を割り当てる1行だけが変更されます(図5)。
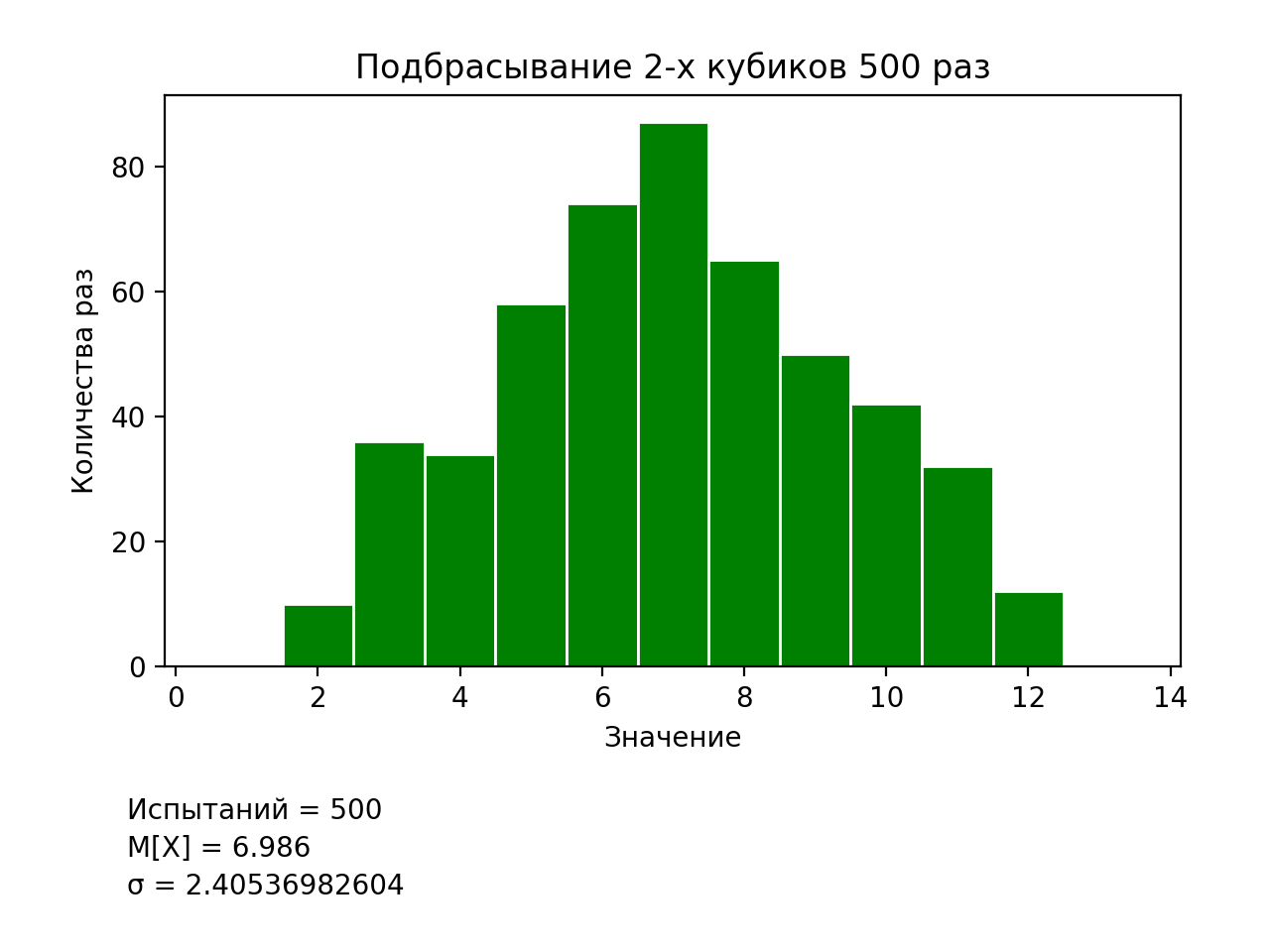
図4 2つのサイコロのトスのシミュレーション結果
... # values = [] for i in range(trials): mu = 7 sigma = 2.4 values.append(random.normalvariate(mu, sigma)) ...
図5 正規分布モデルをプログラミングするための修正リストの一部
上記のリストは、ランダムライブラリのnormalvariateメソッドを使用します。これは、それぞれ分布の平均値と標準偏差であるパラメーターmuとsigmaを持つ正規確率分布の値を生成します。 プログラムの結果を図6に示します。
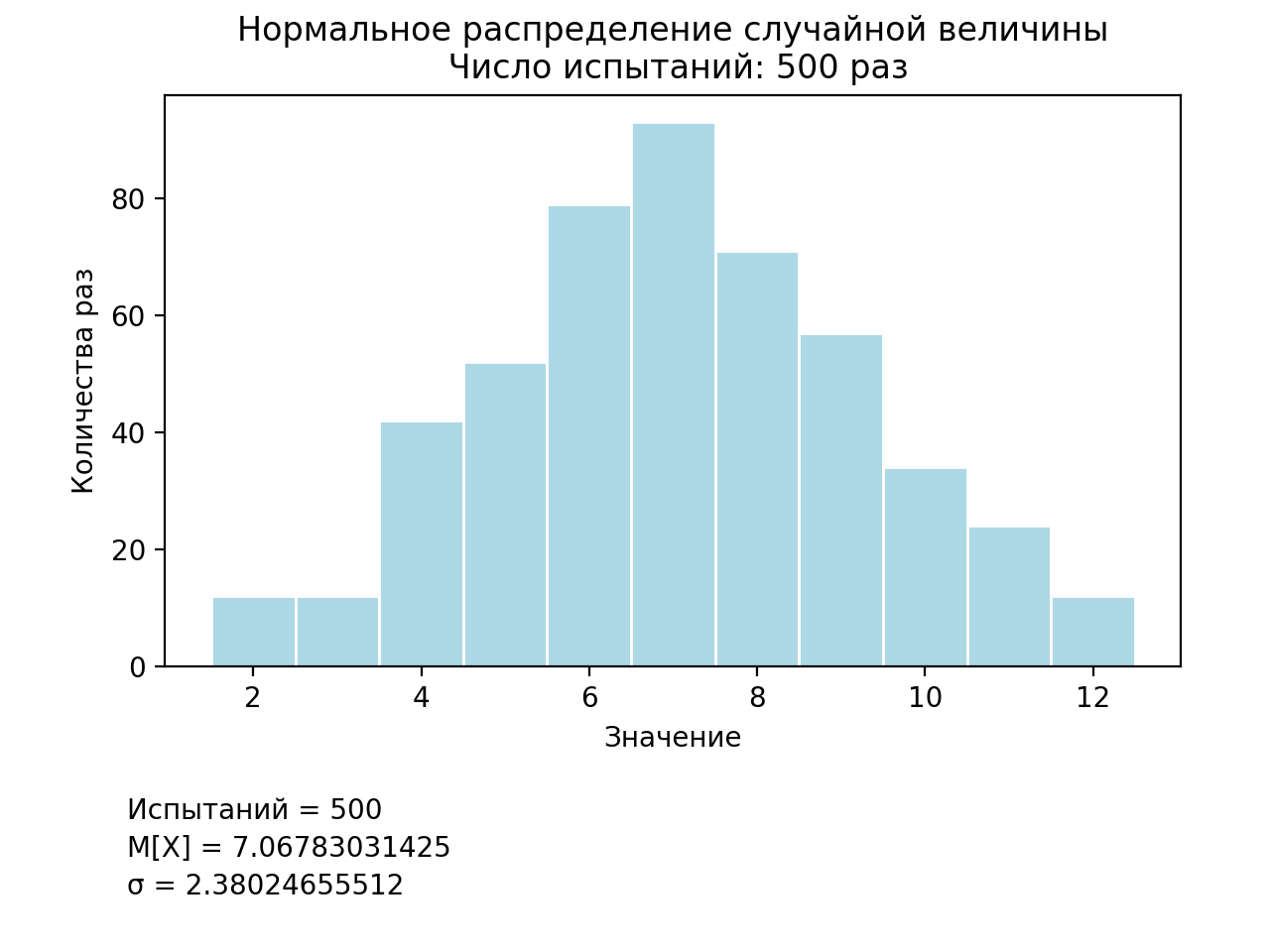
図6 正規分布シミュレーション結果
最後のステップは、指数分布のモデリングです。 指数分布は、多くの場合、さまざまなタイプのキューイングシステムでのアプリケーションの受信の瞬間間の間隔の分布(期間)のモデリングに使用されます。 このリストは、本研究で提示された他のプログラムリストとは若干異なります(図7)。
シミュレーション結果を図8に示します。
... lambd = 10 # values = [] for i in range(trials): values.append(random.expovariate(lambd)) pylab.hist(values, 20, facecolor='lightgreen', edgecolor='white') ...
図7 指数分布モデルをプログラミングするための修正リストの一部
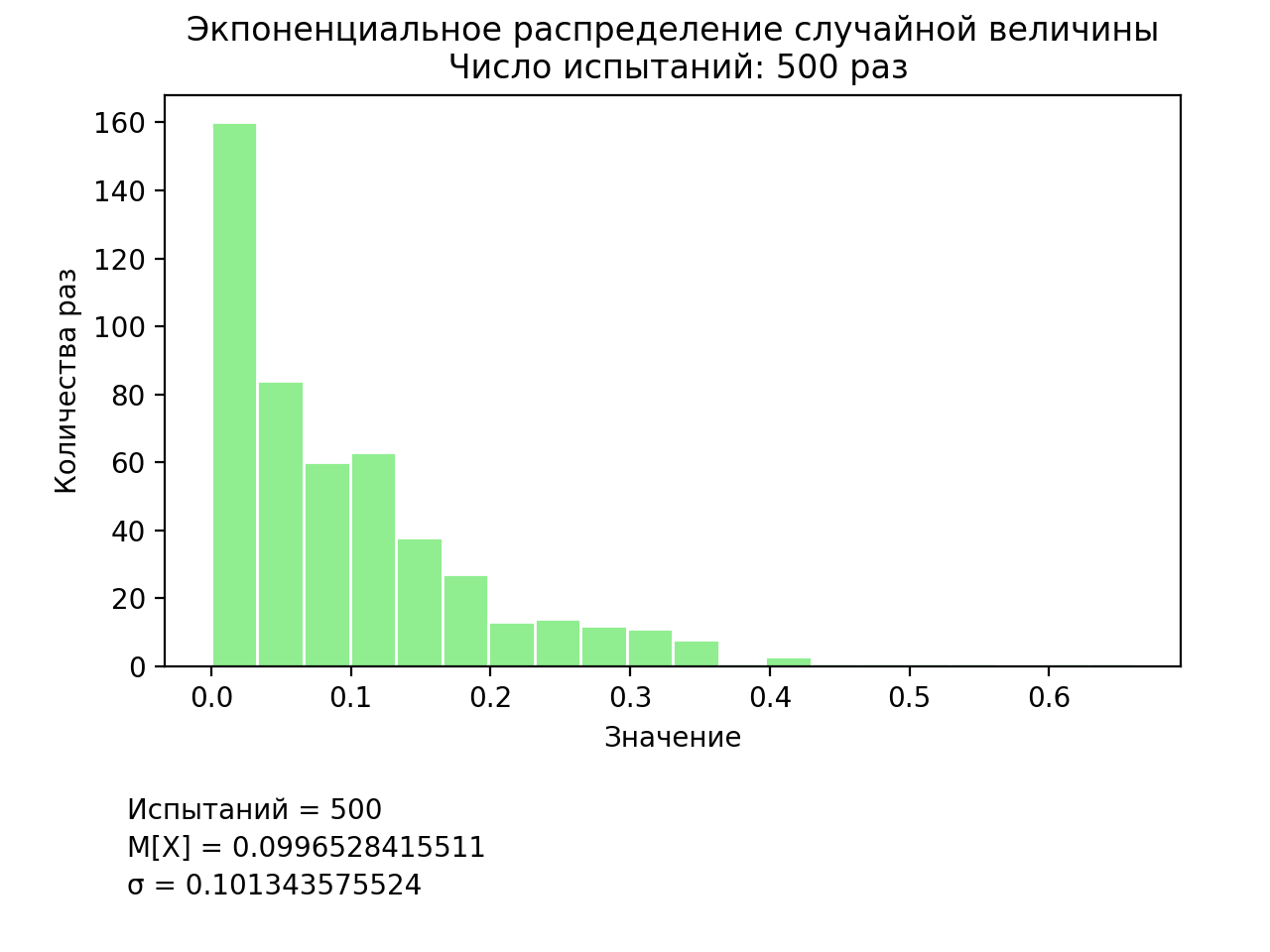
図8 指数分布モデリングの結果
おわりに
この記事では、Pythonでの確率分布モデルのソフトウェア実装をいくつか調べました。 これらのモデルは、独自の実験や研究を行うための基盤を提供します。
この段階では、いくつかの方法とアプローチのみが提示され、将来、著者は確率分布、Pythonプログラミング言語、およびキューイング理論を使用したモデリングのための追加の方法を提示します。