最近ビットコインで起こっていることはすべてピラミッドのように見えるため、特にM. BalandinとV.などの多くの同僚がMMMのおかげで数学的な装置に記事を捧げているため、モデルは適切です。ポイント 。 以前と同様に、Mathcadの計算方法、特にMathcad Expressの無料バージョンでは、予測の精度、ビットコインレートが近い将来にどのようなものになるか、いつクラッシュするかについて主張することなく、主な注意を払います。
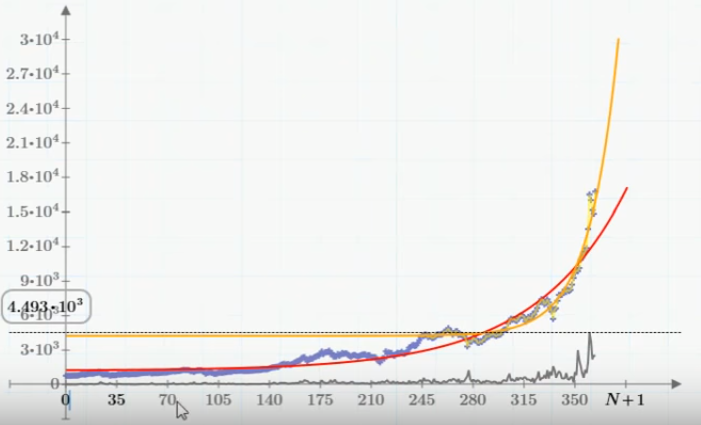
まず、過去数ヶ月間、ビットコインの為替レートのグラフが指数関数的成長に強く似ていることに注意する価値があります(上記のグラフを参照)。 すなわち タイプy '(t)= S * y(t)の方程式の使用を頼みます。その解は指数関数です。 Mathcadで実験データとシミュレーション結果を比較できるようにするには、最初にソースデータをMathcadドキュメントにインポートする必要があります。 これを行う方法(ところで、Mathcad Expressの無料版でもインポートは機能します)では、指数関数を使用してデータを補間および外挿する方法も示したスクリーンキャストを提供しました。 補間外挿の結果は、赤(昨年のデータによる)とオレンジ(4か月)の曲線の上のグラフに示されています。
この記事では、 通常の微分方程式に基づいて、いくつかの単純な既知のモデルを計算します。 それらは当初、生物集団の成長のモデルとして提案され(例えば、 こちらを参照 )、その後、このような経済現象と同様に、流行のモデル化に使用され始めました。 最初のモデルはy '(t)= S * y(t)です。ここでy(t)-時間tでのビットコイン交換レートを考慮します。 この世界的に有名なモデルは、1798年にマルサスが人口成長の法則に関する古典的な作品で提案しました。 人口のダイナミクス、またはむしろ流行の広がりとの類似性を引き出す場合、ビットコインの総資本化を検討するには、y(t)の方が適切です。 現在のレートの値にビットコインの数を掛けた値。 ただし、ビットコインの数は1年でほとんど変化していない(マイニングにより増加している)ため、簡単にするためにy(t)を現在のレートと見なすことができます。
次に、次のモデルであるVerhulst方程式y '= S * y-k * y 2に目を向けます。最後の項では、リソースの制限による流行の減衰を説明します。 したがって、この例を見て、mathcad primeとmathcadで常微分方程式(以降ODE)を解くことができる方法を見てみましょう。 mathcad primeの完全機能バージョンでは、これに「ソリューションブロック」が使用されます。このブロックでは、初期条件、微分方程式自体(黄色で強調表示)、およびそれを解決する組み込みmathcad prime関数が書き込まれます。
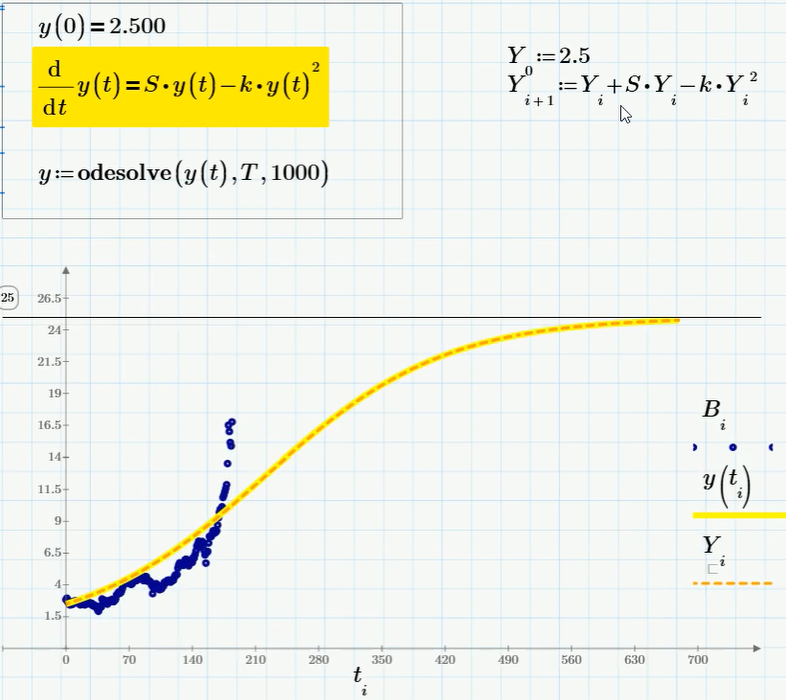
組み込みのMathcad Prime関数を使用したODEソリューションは、黄色の曲線で示されています。 Mathcad Expressの無料バージョンのみをお持ちの場合、ロジスティックソリューションのような単純なODEのソリューションは、差分スキームの実装という形で簡単に書くことができます(Habrに関する詳細な記事はこれに当てられています)。 差分スキーム自体には2行の計算のみが含まれ、フレーム内の「決定ブロック」の右側に書き込まれます。 差分スキームを使用したODEの解は、解y(t)と一致する破線曲線の形で同じグラフに表示されます。 y(t)の傾向がある漸近値はS / kです。 実際、これらの考慮事項に基づいて、係数kが選択されます。 それが実際に何であるかはわかりません(モデルによると、ビットコインは25倍に成長する可能性があります。
次のモデルは、ロジスティックのわずかな複雑さです。つまり、釣りにさらされる人口の動態のモデルです。 特定の割合の人口からの均一な撤退。 ビットコインと類推すると、このモデルは投機家による販売によるビットコインの量の減少を表します(そして/またはお金と交換する際の奇妙な手数料により、ご存じのように10-20%に達します)。 また、取引(ビットコインの販売)は最初からではなく、たとえば平衡値S / kに達した後のある時点から開始することも考慮する価値があります。 方程式とその解法は次のとおりです。
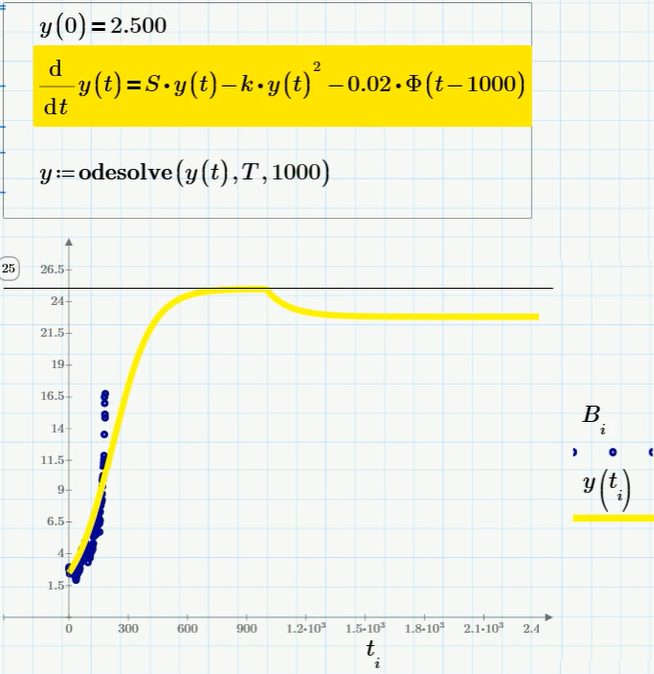
ご覧のように、釣りは平衡速度の特定の減少を引き起こします(計算生物学-人口規模の観点から)。 しかし、これは人口の非常に多くの割合だけが釣りにさらされていない場合に起こります。 方程式の最後の項が大きすぎる(より正確には、特定の臨界値よりも大きい)場合、漸近的な数値を求めるのではなく、人口が消滅します(例えば、ビットコイン交換レートはゼロに崩壊します)。 対応するソリューションスケジュール(最後の項が約0.07の係数の場合)を図に示します:
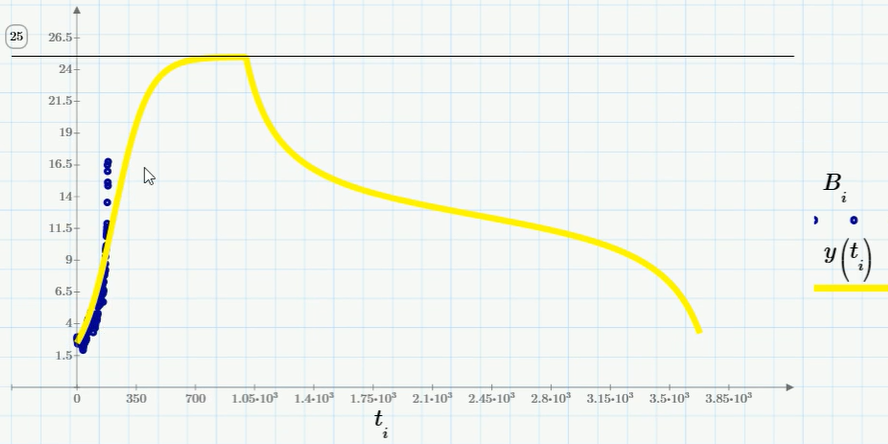
実際、これはすでに金融ピラミッドを非常によく説明しています:最初に、急速な指数関数的成長(マルサスモデル)-次に飽和し、プラトーに達する(Verhulstモデルまたはわずかな漁獲量を持つロジスティックモデル)-そして最後に、投資家の不満、パニックセールスおよび減価償却がゼロになります。 これはいつ起こりますか? もちろん、私は予測することを約束しません-おそらく明日、あるいは1年以内に。
財務モデリングの特徴であり、私が検討したい最後のモデルは、「遅延のあるロジスティックモデル」です。 成長市場でプレーする投機家の存在を考慮したい場合、最も簡単な方法は、彼らがビットコインを購入し、しばらく保留してから販売することを予測することです。 明確にするために、この期間を120日に選択します。 次に、対応する「遅延のあるロジスティック方程式」は、Verhulst方程式y '= S * y-k * y 2とはわずかに異なります。 120日で区切られた2つの時点で。 これは、よく知られている方程式y '(t)= S * y(t)-k * y(t)* y(t-120)でもあり、Mathcad Expressの次の差分方程式を使用して数値的に解くことができます。
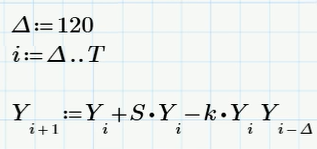
遅延方程式に減衰振動の形の解があることは注目に値します。 そして、崩壊の前に、私たちが見るかもしれない(またはたぶん今すぐ観察さえする)可能性があります。 ただし、この記事は、Mathcadで微分方程式がどのように解決されるかを示し、計算生物学のモデルについて読者に思い出させる良い機会であるため、推測したくありません。
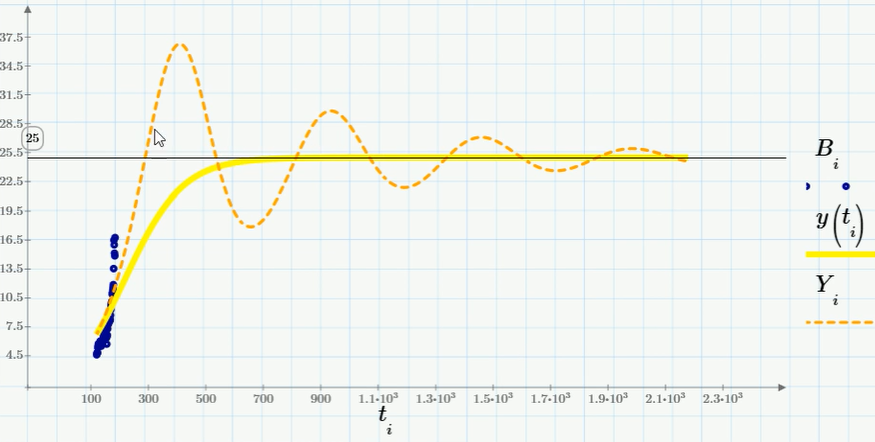
結論として、上記のモデルを計算するためのMathcadの一連のアクションの詳細を説明するビデオへのリンクを残します。