この記事では、例としてFlickrネットワークを使用して 、 リンク予測問題を解決するために変更点を適用する方法について説明します。

移行ポイント:理論と実践
そのため、統計では、特定の数量の分布が変化するポイントが呼び出されます。 ソーシャルネットワークに関しては、移行ポイントを決定できるプロセスの1つは、動的なネットワークで時間内に新しい接続が出現するプロセスです。 これらのポイントを決定するために、次のメトリックのいずれかを使用できます: グラフ密度 、平均間の中心性 、または平均的な中心性 。
これら3つの指標の本質を簡単に説明しましょう。 最も単純なグラフ密度から始めましょう。 ある時点でグラフ密度のダイナミクスに急激な変化がある場合、これはおそらく時間に依存する新しい結合の数の分布の変化によるものです。
中心性メトリックについて説明する場合、 中間中心性は、最短パスが特定の頂点を通過する頻度の尺度であり、 近接中心 性は、グラフの特定の頂点から他のすべての頂点に到達できる速さの尺度として機能します。
McCulloh、Matthew Webb、John Grahamの記事「ソーシャルネットワークにおける変化の検出」は、国際テロリストネットワークAl-Qaeda(グループのメンバー間のつながり)の研究を数年にわたって実施しました。 次の図は、さまざまな離散時間におけるネットワークの特性を示しています。
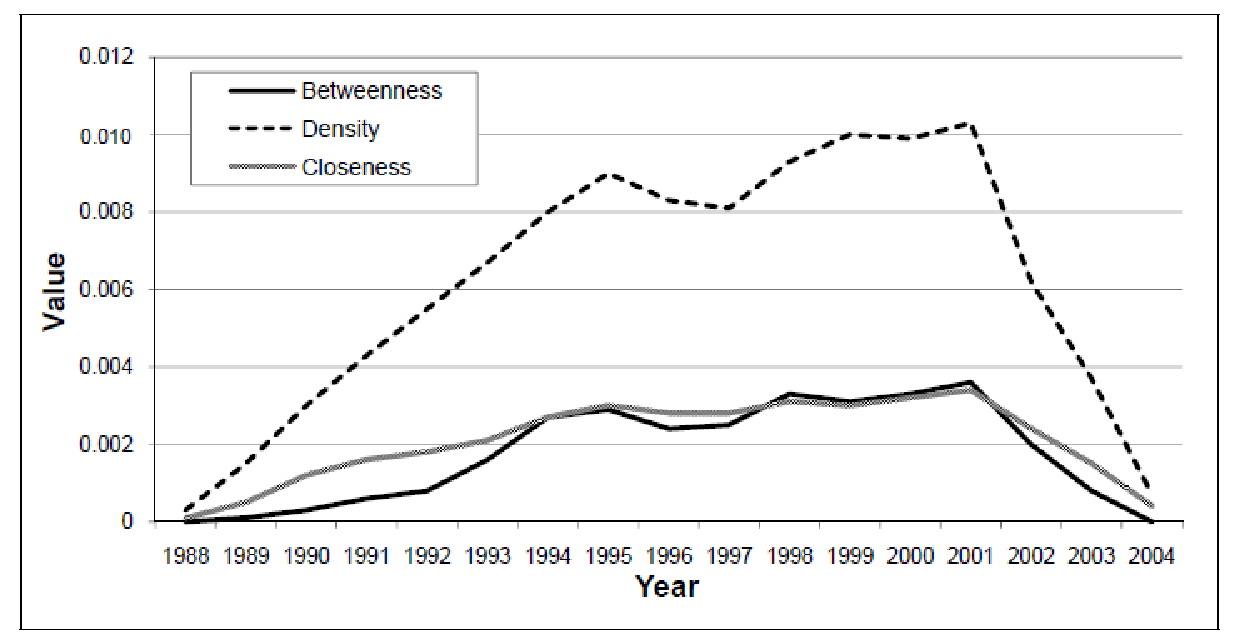
明らかに、2001年以降の分布に予想される変化があります。 2001年9月11日のテロ攻撃の後、アルカイダは世界の特別なサービスの厳格な管理下に置かれ、組織の活動が妨げられたため(同時に、ネットワーク参加者間の接続数の増加は大幅に遅くなったため)、これは経験的に確認されています。 上記の指標は、理論的にはソーシャルネットワークの移行ポイントを識別するのに適していることがわかります。
Flickrネットワーク実験
Flickrネットワークの接続のダイナミクスを予測してみましょう。 メトリックとして、ジャカード係数(近傍法)、ローカルクラスタリング係数の合計(頂点のプロパティに基づくメトリック)、ノード中心性の3つの主な測定値(頂点の各ペア、次数中心性の合計、近接中心性の合計および中間中心性の合計)および最短の値を選択しますマイナス記号でとられた頂点間の距離。
次の瞬間に頂点のペアが結合する確率は、前の瞬間のメトリックの値だけでなく、若干のタイムラグがある瞬間にも依存すると仮定します。 この選択は、時間とともに分類子のインジケータの増加が観察される場合、次の各ステップで2つの頂点が接続される確率が増加するという事実によって説明されます。
それとは別に、ネットワーク内の移行ポイントの識別を担当するインジケーターが含まれていることに注意してください。 単一のツリー内でランダムフォレストを使用する場合、仮定により、リストされた(または複数の)予測子の1つのしきい値がネットワーク分布の瞬間を自動的に決定するため、選択は、密度の絶対値、平均中間中心性、および平均近接中心性を優先して行われます。
ターゲット変数として、 Linkインジケーターを選択します-選択した頂点のペア間の接続の有無(1-エッジで接続された頂点の場合、0-それ以外の場合)。 ランダムフォレスト法による2クラス分類問題の解法では、テストサンプルで次の結果が得られました。

この場合、重要度が等しいクラスに解決されるのはバイナリ分類問題だけではなく、「負」クラスと「正」クラスへの分割です。したがって、AUCメトリックを使用してモデルの品質を判断できます。 AUC = 0.88で、構築されたモデルの高品質について結論付けることができます。
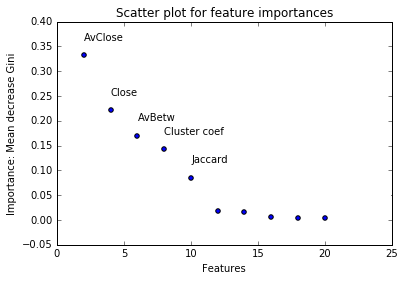
予測変数の意味のある解釈のために、独立変数のGiniインデックスの減少のダイナミクスのグラフを作成します。
結論
- 最も重要な2つの指標はAvCloseとClose(特定の頂点から他のすべての頂点に到達するまでの時間の測定値)=>これらの変数は実際の接続ではなく将来を予測できます
- 重要性の観点から上位3位には、頂点の個々の特性に基づいてではなく、グラフ全体の指標に基づいて計算された2つの指標があります。
- 中間の近さと中心性の重要性は、遷移点の存在の仮説が確認されていることを示唆しています
一般に、遷移点インジケーターの重要性は、決定木のリーフでのトレーニング中に、サンプルが異なる時間間隔のグラフに分割され、その結果、各分岐でのモデルのさらなる構築が同じ予測子の異なるしきい値で発生することを示唆しています。 したがって、遷移点メトリックの導入は、クラスのより正確な予測に役立ちます。