データサイエンティストが第1種と第2種のエラーを使用しない理由

昨日、DataScientistsが第1種と第2種のエラーを使用しない理由と、完全性と正確性を導入した理由を再度説明する必要がありました。 ここでは、新しい基準を導入するためだけに直接行うことはありません。

そして、第2種のエラーが単純に表現される場合：

$$

$$O_2 = 1-\ Pi$$

ここで、Πは膨満感です。

次に、第1種の間違いは、完全性と正確性を介して非常に簡単に表現されます（以下を参照）。

しかし、これは歌詞です。 最も重要な質問：

DataScienceが完全性と正確性を使用し、第1種と第2種のエラーについてほとんど話さないのはなぜですか？

誰が知らないか忘れた-猫をお願いします。

ビジネスチャレンジ

HabrはIT-Schnicksのブログであるため、数学的抽象化の使用を最小限に抑え、すぐに例を挙げて説明します。 R＆Cと略される条件付き銀行Roga＆Copytaの RBSでの不正監視の問題を解決するとします。

各支払いトランザクションについて、このトランザクションが不正（詐欺、F）か正当な（本物、G）かを判断する一種の自動エキスパートシステム（ES）を開発したとします。

システムの品質を評価するための「良い」基準を決定し、これらの基準を計算するための式を提供する必要があります。

Roga＆Copytaは小さいが銀行であるため、人々はその中で商売をし、お金以外は何にも興味がありません。 したがって、開発された基準は、可能な限り透過的に表示する必要があります。ESを使用することで、どれだけ利益が得られるのでしょうか。 競合他社のESをインストールすることは有益ですか？

イベントと確率

トランザクションごとに、4つのイベントを定義できます。

1. F _r （実詐欺）-トランザクションが実際に不正である確率。
2. G _r （本物の本物）-トランザクションが実際に正当である確率。
3. F -ESがトランザクションを不正と「決定」する確率。
4. G -ESがトランザクションを正当なものとして「決定」する確率

明らかに、 F _rとG _rは互換性のないイベントです。 同様に、 FとGは互換性がありません。 このため、次の4つの確率を考慮するのが妥当です。

$$

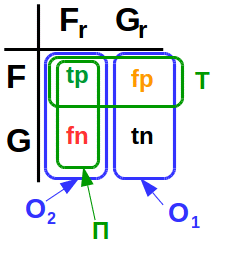
$$tn = P（G G_r）; ~~ fn = P（GF_r）; ~~ fp = P（FG_r）; ~~ tp = P（FF_r）$$

略語は次のようになります。

1. tn-真のネガ
2. fn-偽陰性
3. fp-誤検知
4. tp-真陽性

条件付き確率を考慮することができます ：

$$

$$P（G | G_r）; ~~ P（G | F_r）; ~~ P（F | G_r）; ~~ P（F | F_r）$$

「逆」条件付き確率にも興味があります。

$$ $$表示$$ P（G_k | G）; ~~ P（G_k | F）; ~~ P（F_r | G）; ~~ P（F_r | F）$$表示$$

たとえば、確率 $$$P（F_r | F）$ 以下を意味します。

ESがこのイベントを不正であると「識別」した場合、トランザクションが実際に不正であると判明する可能性はどのくらいですか。

すべきではない $$$P（F_r | F）$ と混同される $$$P（F | F_r）$ 、次の言葉で定義できます：

トランザクションが本当に不正である場合、ESがトランザクション不正を「呼び出す」可能性はどのくらいですか。

同様に、他の条件付き確率を言葉で定義できます。

定義を思い出してください

統計では、 帰無仮説（H ₀ ）と対立仮説（H ₁ ）仮説について話します 。 通常、「自然な」状態は帰無仮説の下で定義されます。 不正監視の場合、「自然な」状態とは、トランザクションが正当なものであるということです。 不正なトランザクションの数が正当なトランザクションの数よりもはるかに少ないという理由だけである場合、これは本当に合理的です。

したがって、帰無仮説の場合はG _rを使用し、代替の場合はF _{rを使用し}ます。

第1（O ₁ ）および第2（O ₂ ）の種類のエラーは、次のように定義されます。

$$

$$O_1 \ stackrel {\ mathrm {def}} {=} P（F | G_r）; ~~~~ O_2 \ stackrel {\ mathrm {def}} {=} P（G | F_r）$$

注 ：多くの場合、第1種のエラーは偽陽性と呼ばれ、第2種のエラーは偽陰性と呼ばれます。 含む、 これらはウィキペディア上の定義です。 これは本質的に真実です。 でも $$$fp = P（FG_r）\ neq P（F | G_r）= O_1$ そして $$$fn = P（GF_r）\ neq P（G | F_r）= O_2$ 。 DataScienceの新規参入者の多くがこの間違いを犯し、混乱しています。

定義による完全性（P）および精度（T）：

$$

$$\ Pi \ stackrel {\ mathrm {def}} {=} P（F | F_r）; ~~~~ T \ stackrel {\ mathrm {def}} {=} P（F_r | F）$$

すなわち 完全性とは、トランザクションが本当に不正であるという条件で、ESがトランザクションを不正であると「判断」する確率です。 ESがトランザクションを不正と「識別」した場合、正確性はトランザクションが本当に不正である可能性です。

完全性と正確性は、次のようにtp 、 fp 、 fnで表すことができます。

$$

$$\ Pi = \ frac {tp} {tp + fn}; ~~ T = \ frac {tp} {tp + fp}$$

完全性と正確性の定義として頻繁に引用されるのはこれらの式であることに注意してください。 これは好みの問題です。 正方形はすべての辺が等しい長方形であり、直角のひし形が正方形であることを証明できます。 またはその逆。 たとえば、私が学校にいたとき、私の正方形は直角の菱形として定義され、同じ辺を持つ長方形が正方形であることが証明されました。

しかし、まだ完全性の定義は $$$\ Pi \ stackrel {\ mathrm {def}} {=} P（F | F_r）$ Tのような精度 $$$\ stackrel {\ mathrm {def}} {=} P（F_r | F）$ 私にはもっと正しいようです。 これらの量の物理的な意味が何であるかはすぐにわかります。 それらが必要な理由は明らかです。

ビジネスの完全性と正確性

Roga＆Copytaのシステムを、 80％のフルネスと10％の精度で作成したとします。

ESがなければ、銀行は詐欺で年間10億人の Tugriks（₮）を失います。 これは、ESのおかげで8億₮の盗難を防止できることを意味します。 さらに2億Thereが残ります-これは銀行（または銀行の顧客）に対する損害であり、ESを防ぐことができませんでした。

10％の精度はどうですか？ この値は、100個のESトランザクションのうち、ターゲットにヒットするのは10個だけであり、その他の場合は正当なトランザクションを中断することを意味します。 それは良いですか悪いですか？

まず、トランザクションが停止すると、銀行はいくつかのアクションを実行します。 たとえば、顧客に電話して操作を確認します。

第二に、正当なトランザクションをブロックすることも常に良い考えではありません。 あなたがレストランで女の子と一緒に座って、請求書を求め、カードで支払いをしていると想像してください...そして、強打します... ESはあなたが詐欺師であると誤って計算しました...おそらくそれは若い女性にはあまり便利ではないでしょう...

したがって、1回の通話に1000 costsかかると仮定します。 また、ハッカーの平均的なチェックは10万checkであると想定しています。

詐欺を8億₮防止するため、平均して8,000件の正しい詐欺取引が発生します。 しかし、精度から判断すると、8000はわずか10％です。 したがって、合計で80,000回呼び出します。 この数字に1回の通話のコスト（1000₮）を掛けると、最大8000万₮になります！

R＆Cバンクの年間損害総額は200 + 80 = 2億8,000万₮です。 しかし、ESがなければ、銀行は10億を失うことになります。 その結果、R＆Cの利益は7億2,000万人です。

第1種および第2種のビジネス上のミス

第2種のエラーは、完全性から推定される基本的なものです。

$$

$$O_2 = 1-\ Pi$$

式の導出は基本的です（次の段落を参照）

したがって、考慮すべきこと-完全性または見逃された詐欺（第2種の間違い）は、大きな違いを表すものではありません。

第一種のエラーはどうですか？

$$

$$O_1 \ stackrel {\ mathrm {def}} {=} P（F | G_r）$$

これが正当な場合、ESがトランザクションを不正操作と呼ぶ可能性があります。 問題は、正当な取引が著しく不正であることです。 1秒間に50を超える支払い取引を行う銀行があります...そしてこれは制限ではありません。

R＆Cは小さな銀行であり、1秒間に5つの支払いトランザクションのみがあります。 1日あたりの金額を計算してみましょう。

$$

$$5 \ cdot 60 \ cdot 60 \ cdot 24 = $ 432,00$$

最後の段落では、R＆Cで年間80,000の内訳があること、つまり1日あたり平均80,000 / 365 = 219.17の内訳があることを学びました 。 これらのうち、ターゲットにヒットしたのはわずか10％（精度です）、つまり22です。つまり、残りは432000-22 = 431978です。

完全性は80％であるため、これら22個のうち4.4個のみが欠落します。

したがって、最初の種類の間違い：

$$

$$O_1 = \ frac {4.4} {431978} = $ 0.00001018$$

値が小さすぎる！ ビジネスはそのような数字を好みません。 また、正確性のためにビジネスの利益と損害を計算するよりも困難です。 そしてもう1つ問題があります。

最初の種類の間違いにより、銀行の決済取引の量を間接的に理解できます！

精度に関しては、このような問題はありません。 R＆Cセキュリティの専門家は、詐欺の程度を認識しています。 彼らは、最も重要な少女からコンタクトセンターの許容負荷について学び、銀行経営者に希望する完全性について尋ねます。 絶対的な負荷、必要な完全性、および不正の量がわかっていれば、容認できる精度を簡単に計算できます。 これらの2つの数値は、参照条件（または入札）に適合します。

開発者には、不正で正当な取引のサンプルが提供されます。 サンプルが代表的な場合、このデータで十分です。

純粋な数学の観点から見た「間違った」精度

トランザクションの量が2倍になると、精度が低下します。 詐欺の量が2倍になれば、精度も向上します。第1種のエラーにはこのような問題はありません。したがって、「純粋な数学」の観点からすると、この値ははるかに「正確」です。

しかし、実際には、詐欺の量が急激に増加した場合、それは原則として新しいタイプの詐欺であり、ESはそれを捕まえるために訓練されていません...正確さは同じままです（しかし、捕まえられない詐欺があるため、完全性は低下します）。 正当なトランザクションの数の増加に関しては、この増加は緩やかであり、「不意打ち」はありません。

したがって、 実際には、精度は電力の品質を評価するための素晴らしい、ビジネスに優しい基準です。

第1種および第2種の完全性と精度のエラーの結論

しかし、正確さによって最初の種類のエラーを推定するためのエレガントな式があるのでしょうか？

ここに第二の間違い、すべてがどれほど美しいかがあります：

$$

$$O_2 = 1-\ Pi$$

残念ながら、O ₁ではそれほどエレガントに機能しません。 精度（T）と完全性（P）の比率は次のとおりです。

$$

$$O_1 = \ frac {P（F_r）} {P（G_r）} \ cdot \ Pi \ cdot \ left（\ frac {1} {T}-1 \ right）$$

おわりに

精度と完全性は、第1種および第2種のエラーよりも「悪くない」および「良くない」です。 それはすべてタスクに依存します。 大さじ1杯のケーキは食べませんが、ティーボルシチは食べますか？ 可能ですが。

精度と完全性は、より理解しやすい品質基準です。 操作が簡単です。 それらを使用すると、不正監視タスクで防止された損害を簡単に計算できます。

_{タイプミスや文法の間違いを見つけた場合は、個人で書いてください。}