問題の概要と説明
私の大学での3年目の研究では、c ++で昇順(度t = 2)にソートされた一意のキーを含むBツリーを実装するタスクに直面しました(アイテムを追加、削除、検索し、それに応じてツリーを再構築します) 。
Habréに関するいくつかの記事(たとえば、 Bツリー 、 2〜3 ツリー 、 ナイーブな実装など)を再読 すると、すべてが明確であるように見えます。 理論的にのみ、実際にはそうではありません。 しかし、私はこれらの困難に対処することができました。 私の投稿の目的は、得られた経験をユーザーと共有することです。
いくつかのハイライト
Bツリーは、次のプロパティを満たすツリーです。
1.各ノードには少なくとも1つのキーが含まれています。 ルートには1〜2t-1のキーが含まれます。 他のノードには、t-1から2t-1のキーが含まれます。 葉もこの規則の例外ではありません。 ここで、tは2以上のツリーパラメーターです。
2.葉には子孫がありません。 n個のキーを含む他のノードには、n + 1個の子孫が含まれます。 この場合:
a)最初の子孫と彼のすべての子孫には、間隔からのキーが含まれます
b)のために
c)(n + 1)番目の子孫およびそのすべての子孫には、間隔からのキーが含まれます
3.すべての葉の深さは同じです。
実装
まず、ツリーのノード構造を作成します。
ノード構造
const int t=2; struct BNode { int keys[2*t]; BNode *children[2*t+1]; BNode *parent; int count; // int countSons; // bool leaf; };
次に、適切なメソッドを含むTreeクラスを作成します。
クラスツリー
class Tree { private: BNode *root; void insert_to_node(int key, BNode *node); void sort(BNode *node); void restruct(BNode *node); void deletenode(BNode *node); bool searchKey(int key, BNode *node); void remove(int key, BNode *node); void removeFromNode(int key, BNode *node); void removeLeaf(int key, BNode *node); void lconnect(BNode *node, BNode *othernode); void rconnect(BNode *node, BNode *othernode); void repair(BNode *node); public: Tree(); ~Tree(); void insert(int key); bool search(int key); void remove(int key); };
コンストラクタとデストラクタをすぐに説明してください。 デストラクタでは、ツリーから要素を削除するための再帰的なメソッドが呼び出されます。
コンストラクタとデストラクタ
Tree::Tree() { root=nullptr; } Tree::~Tree(){ if(root!=nullptr) deletenode(root); } void Tree::deletenode(BNode *node){ if (node!=nullptr){ for (int i=0; i<=(2*t-1); i++){ if (node->children[i]!=nullptr) deletenode(node->children[i]); else { delete(node); break; } } } }
まず、キーをノードに追加することを検討してください 。 私の場合(t = 2)は次のようになります。
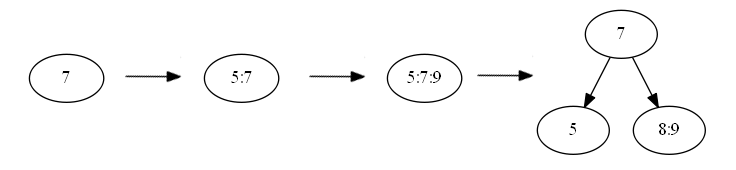
つまり、ノードに3つ以上の要素があるとすぐに、ノードが壊れます。
そのため、ツリーに要素を追加するには、いくつかのメソッドを実装する必要があります。
1つ目は、ノードへの単純な追加です。 このメソッドは、ツリーの値の増加に関する条件を満たすために必要な並べ替えメソッドを呼び出します。 2番目の方法は
目的の位置が以前に検索されたノードに値を追加し、
必要な場合(ノードには3つ以上の要素があります)、3番目のメソッド-ノードを親と2人の息子に分割するメソッドが呼び出されます。
最初の方法は、単純なaddメソッドです。
簡単な追加方法
void Tree::insert_to_node(int key, BNode *node){ node->keys[node->count]=key; node->count=node->count+1; sort(node); }
ノード内の数値をソートする方法 :
選別方法
void Tree::sort(BNode *node) { int m; for (int i=0; i<(2*t-1); i++){ for (int j=i+1; j<=(2*t-1); j++){ if ((node->keys[i]!=0) && (node->keys[j]!=0)){ if ((node->keys[i]) > (node->keys[j])){ m=node->keys[i]; node->keys[i]=node->keys[j]; node->keys[j]=m; } } else break; } } }
ここではすべてが明確だと思います。
2番目の方法は、位置の予備検索でノードに値を追加する方法です。
予備検索でサイトに追加する方法
void Tree::insert(int key){ if (root==nullptr) { BNode *newRoot = new BNode; newRoot->keys[0]=key; for(int j=1; j<=(2*t-1); j++) newRoot->keys[j]=0; for (int i=0; i<=(2*t); i++) newRoot->children[i]=nullptr; newRoot->count=1; newRoot->countSons=0; newRoot->leaf=true; newRoot->parent=nullptr; root=newRoot; } else { BNode *ptr=root; while (ptr->leaf==false){ // , for (int i=0; i<=(2*t-1); i++){ // if (ptr->keys[i]!=0) { if (key<ptr->keys[i]) { ptr=ptr->children[i]; break; } if ((ptr->keys[i+1]==0)&&(key>ptr->keys[i])) { ptr=ptr->children[i+1]; // , "" break; } } else break; } } insert_to_node(key, ptr); while (ptr->count==2*t){ if (ptr==root){ restruct(ptr); break; } else { restruct(ptr); ptr=ptr->parent; } } } }
3番目の方法は、ノード分割方法です。
ノード分割方法
void Tree::restruct(BNode *node){ if (node->count<(2*t-1)) return; // BNode *child1 = new BNode; int j; for (j=0; j<=t-2; j++) child1->keys[j]=node->keys[j]; for (j=t-1; j<=(2*t-1); j++) child1->keys[j]=0; child1->count=t-1; // if(node->countSons!=0){ for (int i=0; i<=(t-1); i++){ child1->children[i]=node->children[i]; child1->children[i]->parent=child1; } for (int i=t; i<=(2*t); i++) child1->children[i]=nullptr; child1->leaf=false; child1->countSons=t-1; // } else { child1->leaf=true; child1->countSons=0; for (int i=0; i<=(2*t); i++) child1->children[i]=nullptr; } // BNode *child2 = new BNode; for (int j=0; j<=(t-1); j++) child2->keys[j]=node->keys[j+t]; for (j=t; j<=(2*t-1); j++) child2->keys[j]=0; child2->count=t; // if(node->countSons!=0) { for (int i=0; i<=(t); i++){ child2->children[i]=node->children[i+t]; child2->children[i]->parent=child2; } for (int i=t+1; i<=(2*t); i++) child2->children[i]=nullptr; child2->leaf=false; child2->countSons=t; // } else { child2->leaf=true; child2->countSons=0; for (int i=0; i<=(2*t); i++) child2->children[i]=nullptr; } // if (node->parent==nullptr){ // , node->keys[0]=node->keys[t-1]; for(int j=1; j<=(2*t-1); j++) node->keys[j]=0; node->children[0]=child1; node->children[1]=child2; for(int i=2; i<=(2*t); i++) node->children[i]=nullptr; node->parent=nullptr; node->leaf=false; node->count=1; node->countSons=2; child1->parent=node; child2->parent=node; } else { insert_to_node(node->keys[t-1], node->parent); for (int i=0; i<=(2*t); i++){ if (node->parent->children[i]==node) node->parent->children[i]=nullptr; } for (int i=0; i<=(2*t); i++){ if (node->parent->children[i]==nullptr) { for (int j=(2*t); j>(i+1); j--) node->parent->children[j]=node->parent->children[j-1]; node->parent->children[i+1]=child2; node->parent->children[i]=child1; break; } } child1->parent=node->parent; child2->parent=node->parent; node->parent->leaf=false; delete node; } }
searchでは、trueまたはfalseを返す次のメソッドが実装されました(2番目のメソッドは再帰的です)。
検索する
bool Tree::search(int key){ return searchKey(key, this->root); } bool Tree::searchKey(int key, BNode *node){ if (node!=nullptr){ if (node->leaf==false){ int i; for (i=0; i<=(2*t-1); i++){ if (node->keys[i]!=0) { if(key==node->keys[i]) return true; if ((key<node->keys[i])){ return searchKey(key, node->children[i]); break; } } else break; } return searchKey(key, node->children[i]); } else { for(int j=0; j<=(2*t-1); j++) if (key==node->keys[j]) return true; return false; } } else return false; }
ノードからキーを削除する方法の実装は最も困難でした。 実際、いくつかのケースでは、削除は隣接するノードを接着する必要があり、いくつかのケースでは、「兄弟」のノードから値を取得する必要があります。 例:
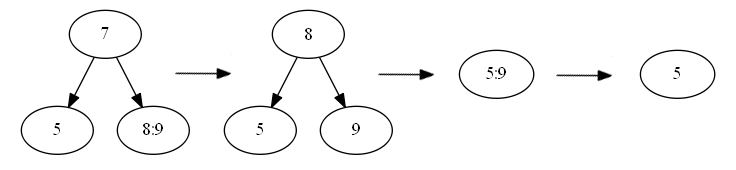
削除はいくつかの場合です。 最初の方法は、ノードからキーを削除する簡単な方法です。
ノードからキーを削除する方法
void Tree::removeFromNode(int key, BNode *node){ for (int i=0; i<node->count; i++){ if (node->keys[i]==key){ for (int j=i; j<node->count; j++) { node->keys[j]=node->keys[j+1]; node->children[j]=node->children[j+1]; } node->keys[node->count-1]=0; node->children[node->count-1]=node->children[node->count]; node->children[node->count]=nullptr; break; } } node->count--; }
2番目のケースでは、キーを削除した後、隣接ノードを接続する必要があります。 したがって、2番目と3番目の方法は、ノードを接続する方法です 。
ノード結合方法
void Tree::lconnect(BNode *node, BNode *othernode){ if (node==nullptr) return; for (int i=0; i<=(othernode->count-1); i++){ node->keys[node->count]=othernode->keys[i]; node->children[node->count]=othernode->children[i]; node->count=node->count+1; } node->children[node->count]=othernode->children[othernode->count]; for (int j=0; j<=node->count; j++){ if (node->children[j]==nullptr) break; node->children[j]->parent=node; } delete othernode; } void Tree::rconnect(BNode *node, BNode *othernode){ if (node==nullptr) return; for (int i=0; i<=(othernode->count-1); i++){ node->keys[node->count]=othernode->keys[i]; node->children[node->count+1]=othernode->children[i+1]; node->count=node->count+1; } for (int j=0; j<=node->count; j++){ if (node->children[j]==nullptr) break; node->children[j]->parent=node; } delete othernode; }
4番目の方法は、結び目を「固定する」方法です 。 この方法では、Bツリーのすべての条件が満たされるまで、ツリーは文字通り再構築されます。
ノードを「修正」する方法
void Tree::repair(BNode *node){ if ((node==root)&&(node->count==0)){ if (root->children[0]!=nullptr){ root->children[0]->parent=nullptr; root=root->children[0]; } else { delete root; } return; } BNode *ptr=node; int k1; int k2; int positionSon; BNode *parent=ptr->parent; for (int j=0; j<=parent->count; j++){ if (parent->children[j]==ptr){ positionSon=j; // break; } } // ptr- ( ) if (positionSon==0){ insert_to_node(parent->keys[positionSon], ptr); lconnect(ptr, parent->children[positionSon+1]); parent->children[positionSon+1]=ptr; parent->children[positionSon]=nullptr; removeFromNode(parent->keys[positionSon], parent); if(ptr->count==2*t){ while (ptr->count==2*t){ if (ptr==root){ restruct(ptr); break; } else { restruct(ptr); ptr=ptr->parent; } } } else if (parent->count<=(t-2)) repair(parent); } else { // ptr- ( ) if (positionSon==parent->count){ insert_to_node(parent->keys[positionSon-1], parent->children[positionSon-1]); lconnect(parent->children[positionSon-1], ptr); parent->children[positionSon]=parent->children[positionSon-1]; parent->children[positionSon-1]=nullptr; removeFromNode(parent->keys[positionSon-1], parent); BNode *temp=parent->children[positionSon]; if(ptr->count==2*t){ while (temp->count==2*t){ if (temp==root){ restruct(temp); break; } else { restruct(temp); temp=temp->parent; } } } else if (parent->count<=(t-2)) repair(parent); } else { // ptr insert_to_node(parent->keys[positionSon], ptr); lconnect(ptr, parent->children[positionSon+1]); parent->children[positionSon+1]=ptr; parent->children[positionSon]=nullptr; removeFromNode(parent->keys[positionSon], parent); if(ptr->count==2*t){ while (ptr->count==2*t){ if (ptr==root){ restruct(ptr); break; } else { restruct(ptr); ptr=ptr->parent; } } } else if (parent->count<=(t-2)) repair(parent); } } }
5番目の方法は、 シートからキーを削除する方法です。
シートからキーを削除する方法
void Tree::removeLeaf(int key, BNode *node){ if ((node==root)&&(node->count==1)){ removeFromNode(key, node); root->children[0]=nullptr; delete root; root=nullptr; return; } if (node==root) { removeFromNode(key, node); return; } if (node->count>(t-1)) { removeFromNode(key, node); return; } BNode *ptr=node; int k1; int k2; int position; int positionSon; int i; for (int i=0; i<=node->count-1; i++){ if (key==node->keys[i]) { position=i; // break; } } BNode *parent=ptr->parent; for (int j=0; j<=parent->count; j++){ if (parent->children[j]==ptr){ positionSon=j; // break; } } // ptr- ( ) if (positionSon==0){ if (parent->children[positionSon+1]->count>(t-1)){ // , t-1 k1=parent->children[positionSon+1]->keys[0]; //k1 - k2=parent->keys[positionSon]; //k2 - , , , , k1 insert_to_node(k2, ptr); removeFromNode(key, ptr); parent->keys[positionSon]=k1; // k1 k2 removeFromNode(k1, parent->children[positionSon+1]); // k1 } else { // <u></u> t-1 removeFromNode(key, ptr); if (ptr->count<=(t-2)) repair(ptr); } } else { // ptr- ( ) if (positionSon==parent->count){ // , t-1 if (parent->children[positionSon-1]->count>(t-1)){ BNode *temp=parent->children[positionSon-1]; k1=temp->keys[temp->count-1]; //k1 - k2=parent->keys[positionSon-1]; //k2 - , , , k1 insert_to_node(k2, ptr); removeFromNode(key, ptr); parent->keys[positionSon-1]=k1; removeFromNode(k1, temp); } else { // <u></u> t-1 removeFromNode(key, ptr); if (ptr->count<=(t-2)) repair(ptr); } } else { // ptr // , t-1 if (parent->children[positionSon+1]->count>(t-1)){ k1=parent->children[positionSon+1]->keys[0]; //k1 - k2=parent->keys[positionSon]; //k2 - , , , k1 insert_to_node(k2, ptr); removeFromNode(key, ptr); parent->keys[positionSon]=k1; // k1 k2 removeFromNode(k1, parent->children[positionSon+1]); // k1 } else { // , t-1 if (parent->children[positionSon-1]->count>(t-1)){ BNode *temp=parent->children[positionSon-1]; k1=temp->keys[temp->count-1]; //k1 - k2=parent->keys[positionSon-1]; //k2 - , , , k1 insert_to_node(k2, ptr); removeFromNode(key, ptr); parent->keys[positionSon-1]=k1; removeFromNode(k1, temp); } else { // t-1 removeFromNode(key, ptr); if (ptr->count<=(t-2)) repair(ptr); } } } } }
6番目の方法は、任意のノードからの削除方法です。
任意のノードから削除する方法
void Tree::remove(int key, BNode *node){ BNode *ptr=node; int position; // int i; for (int i=0; i<=node->count-1; i++){ if (key==node->keys[i]) { position=i; break; } } int positionSon; // if (ptr->parent!=nullptr){ for(int i=0; i<=ptr->parent->count; i++){ if (ptr->children[i]==ptr){ positionSon==i; break; } } } // ptr=ptr->children[position+1]; int newkey=ptr->keys[0]; while (ptr->leaf==false) ptr=ptr->children[0]; // 1 - // - key , if (ptr->count>(t-1)) { newkey=ptr->keys[0]; removeFromNode(newkey, ptr); node->keys[position]=newkey; } else { ptr=node; // ptr=ptr->children[position]; newkey=ptr->keys[ptr->count-1]; while (ptr->leaf==false) ptr=ptr->children[ptr->count]; newkey=ptr->keys[ptr->count-1]; node->keys[position]=newkey; if (ptr->count>(t-1)) removeFromNode(newkey, ptr); else { // , t-1 - removeLeaf(newkey, ptr); } } }
7番目のメソッドは、ツリーから削除するキー値を入力として取得する削除メソッド自体です。
基本的な取り外し方法
void Tree::remove(int key){ BNode *ptr=this->root; int position; int positionSon; int i; if (searchKey(key, ptr)==false) { return; } else { // , for (i=0; i<=ptr->count-1; i++){ if (ptr->keys[i]!=0) { if(key==ptr->keys[i]) { position=i; break; } else { if ((key<ptr->keys[i])){ ptr=ptr->children[i]; positionSon=i; i=-1; } else { if (i==(ptr->count-1)) { ptr=ptr->children[i+1]; positionSon=i+1; i=-1; } } } } else break; } } if (ptr->leaf==true) { if (ptr->count>(t-1)) removeFromNode(key,ptr); else removeLeaf(key, ptr); } else remove(key, ptr); }
まあ、そのようなもの。 誰かがこの記事を役に立つと思うことを願っています ご清聴ありがとうございました。