はじめに
私の出版物[1,2]では、時間を考慮せずに統計学で経済的問題が考慮されました。 経済ダイナミクスを最適化するタスクでは、経済パラメーターの変化とそれらの時間的関係を分析します。 経済のダイナミクスのモデルでは、時間は離散的であり、たとえば1年以上で急激に変化すると考えることができます。 そのようなプロセスを記述するために、差分方程式が使用されます。 時間の連続的な変化により、微分方程式を使用してモデルパラメーターを記述します。
問題の声明
経済ダイナミクスのモデルを初めて知る場合、2つの標準モデルを検討するだけで十分です。 これはクモの巣型のモデルであり、Caldorモデルとモデルであり、経済力学の記述に対する上記の2つのアプローチが実装されています。
経済力学のクモのようなモデル[3]
このモデルを使用すると、特定の製品の需要曲線と供給曲線で表される、市場の価格と生産量の安定性を調べることができます。 需要関数S(p)は、特定の期間iにおける製品の価格pに対する製品の需要量の依存性を特徴付けます。 供給関数D(p)は、商品の価格に応じて商品の供給量を特徴付けます。 市場の均衡価格pは、需給の平等S(p)= D(p)によって決まります。
製造業者は、前の期間に確立された商品の需要と価格に基づいて、提供される商品の量を決定します-i-1。
この方程式を解くには、初期期間Q0のボリュームを定義し、逆供給関数を使用して商品の価格を決定します。
次の期間の生産量は、需要関数によって決定されます
などなど。
需要と供給の関数が変化した場合、価格の変動は、均衡からの価格の偏差によってのみ決定されます。
ウェブのようなリスト
from scipy.optimize import * import numpy as np import matplotlib.pyplot as plt a=1;b=0.2# def fun_1(x,a): # return np.e**(-a*x**2) def fun_2(x,b): # return b*x**2 x0=round(fsolve(lambda x:fun_1(x,a)-fun_2(x,b),1)[0],3)# x=np.arange(0,x0+1,0.01) plt.figure() plt.title(' ', size=12) plt.xlabel(' ', size=12) plt.plot(x, fun_1(x,a), 'r', linestyle ='--',linewidth = 1, label=' ') plt.plot(x, fun_2(x,b), 'b', linestyle ='-' ,linewidth = 1, label=' ') plt.plot(x0, fun_2(x0,b), marker = 'o', markersize = 6, markerfacecolor = 'g', label=' ' ) plt.plot(x0, 0, marker = 's', markersize = 6, markerfacecolor = 'r', label=' ' ) plt.legend(loc='best') plt.grid(True) q=[];p=[];x=[] q.append(0.6) p.append(round(fsolve(lambda x:fun_1(x,a)-q[0],1)[0],3)) for i in np.arange(0,7): x.append(i) if i!=0: q.append(fun_2(p[i-1],b)) p.append(round(fsolve(lambda x:fun_1(x,a)-q[i],1)[0],3)) plt.figure() plt.title(' ', size=12) plt.xlabel(' ', size=12) plt.plot(x, p, 'r', marker = 's', markersize = 6, markerfacecolor = 'r', label=' ') plt.plot(x, q, 'b', marker = 'o', markersize = 6, markerfacecolor = 'b', label=' ') plt.legend(loc='best') plt.grid(True) plt.show()
プログラム結果
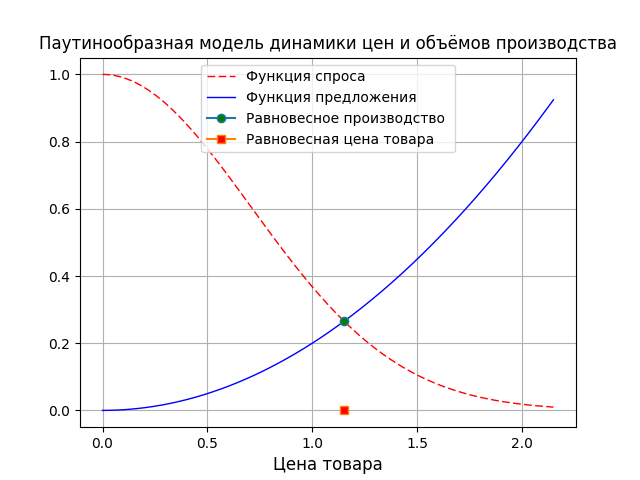
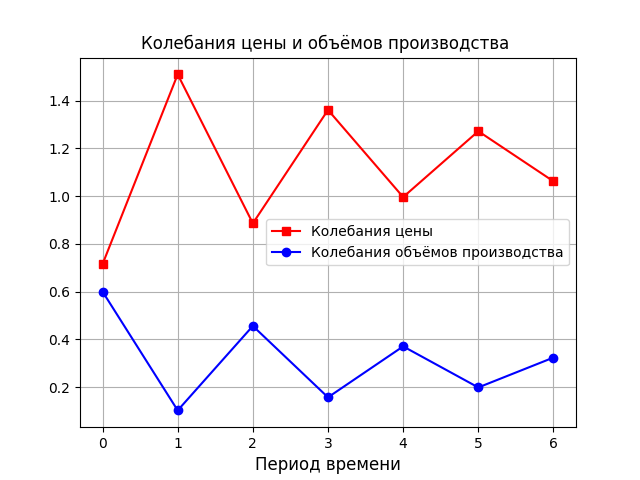
おわりに
商品市場の統計に従って定数a、bを調整することにより(このような分析はscipy.statsで十分に開発されています)、クモの巣のようなモデルを使用して生産量を調整できます。
カルドールモデル[4]
モデルは、貯蓄S(y)と投資I(y)の要因によって、経済活動の変化の周期的な性質を説明しようとします。ここで、yは収入です。 モデルでは、貯蓄と投資の量は線形ではなく、ロジスティック(S字型)関数です。
Caldorモデルのリスト
from scipy.optimize import * from scipy.misc import derivative import numpy as np import matplotlib.pyplot as plt c=2.2;a=-0.9;h=0.1 def f(x): return 3*x-2*c*(a+x)**3+2*a**3-1.5 def s(x): return c*(a+x)**3-a**3+2 def l(x): return 3*xc*(a+x)**3+a**3+0.5 rx=[];ry=[];dy=[];dz=[] for i in np.arange(0,3): x=round(fsolve(lambda x:f(x),i)[0],3) z=derivative(f, x, dx=1e-6) rx.append(x) ry.append(s(x)) dz.append(z) x=[i*h for i in np.arange(0,18)] z=[s(i*h) for i in np.arange(0,18)] v=[l(i*h) for i in np.arange(0,18)] plt.figure() plt.title(' ', size=12) plt.xlabel('', size=12) plt.plot(x, z, 'r', linestyle ='--',linewidth = 2, label=' -s(x)') plt.plot(x, v, 'b', linestyle ='-' ,linewidth = 2, label=' -l(x)') plt.plot(rx[0], ry[0], marker = 's', markersize = 6, label=' y1 - df/dx<0,df/dx= '+ str(round(dz[0],3))) plt.plot(rx[1], ry[1], marker = 'o', markersize = 6, label=' y2 - df/dx>0,df/dx='+ str(round(dz[1],3))) plt.plot(rx[2], ry[2], marker = 's', markersize = 6, label=' y3 - df/dx<0,df/dx= '+ str(round(dz[2],3))) plt.legend(loc='best') plt.grid(True) T=4;N=50; h=T/N y=[];y.append(1.2) z=[];z.append(0.987) u=[];u.append(0.5) x=[ i*h for i in np.arange(0,N+2)] for i in np.arange(1,N+2): y.append(y[i-1]+h*f(y[i-1])) for i in np.arange(1,N+2): z.append(z[i-1]+h*f(z[i-1])) for i in np.arange(1,N+2): u.append(u[i-1]+h*f(u[i-1])) y1= [rx[0] for i in np.arange(0,N+2)] y3= [rx[2] for i in np.arange(0,N+2)] y2= [rx[1] for i in np.arange(0,N+2)] plt.figure() plt.title(' \n ', size=12) plt.plot(x, y,linewidth = 2, label=' f(x0)=1.2') plt.plot(x, z,linewidth = 2, label='f(x0)=0.987') plt.plot(x, u,linewidth = 2, label=' f(x0)=0.5') plt.plot(x, y1,linewidth = 1, label=' y1') plt.plot(x, y3,linewidth = 1, label=' y3') plt.plot(x, y2,linewidth = 1, label='y2') plt.legend(loc='best') plt.grid(True) plt.show()
プログラムの結果は、節約と投資のダイナミクスです。
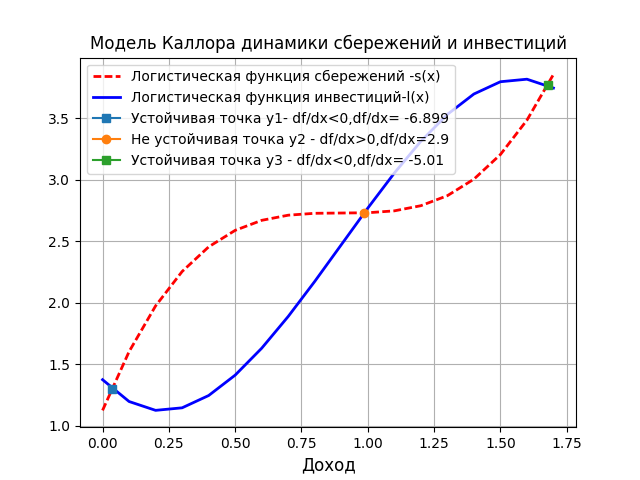
平衡は、S(y)= 1(y)の条件下で達成されます。 チャートにはこのような3つのポイントがあります。 関数f(y)= I(y)-S(y)の導関数は負であるため、2つの安定点y1とy3のみがあります。
このようなシステムでの収入の変化は、初期条件y(0)= y0の下で微分方程式dy / dt = f(y)として表すことができます。
プログラムの結果は、さまざまな初期条件の下での統合収入です。
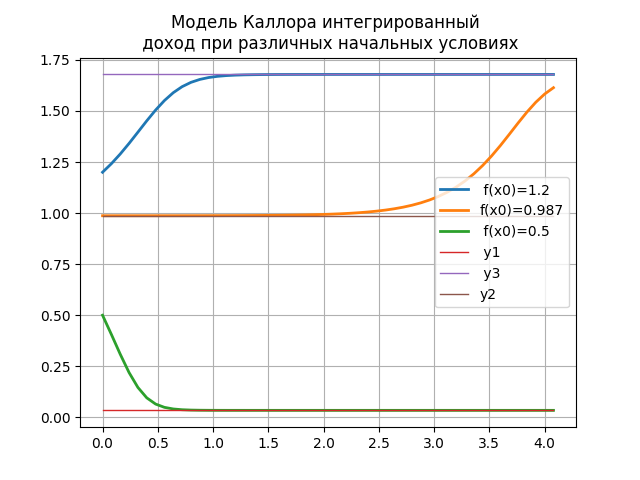
収入の値が平衡状態の1つに対応する場合、無期限に持続できます。 ただし、たとえばポイントy2での不安定な均衡の経済状況の変化は、均衡位置の左または右への移動に応じて、安定ポイントy1またはy3のいずれかに移行します。 平衡位置からのわずかな偏差がある安定したポイントの場合、同じ状態に戻ります。 これは、継続的な投資および節約機能に当てはまります。 事業活動の定期的な変化は、これらの機能の変形につながり、経済発展の周期的な性質を説明し、下のグラフを示します。
おわりに
Kallorモデルを使用して貯蓄と投資の機能に含まれる定数cとaを調整することにより、管理上の決定をサポートする統計を取得できます。
ご清聴ありがとうございました!