はじめに
経済における数学的モデリングは、実際のビジネスで発生する多くの問題の発生を防ぐのに役立ちます。 商品の製造業者の問題の1つは破産です。
したがって、少なくとも初期レベルでは、競争環境で倒産を回避するための戦略に精通することは確かに有用です。 さらに、Pythonの人気が高まっており、この言語での経済的な最適化タスクの実装もPythonの人気に貢献します。
問題の声明
無制限の需要で、ボリュームxとyで類似の商品を生産する2つの競合企業の市場行動のモデルを考えてみましょう[1]。 価格とコストについて次の2つの関数を作成します。
グラフ化された価格とコスト関数のリスト
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt a=10 def f(q): return a*np.e**(-0.5*q**2) def h(q): # return np.sqrt(q) plt.figure() q= np.arange(0, 2.01, 0.1)# plt.title(r'$y=f(q)$') # TeX plt.ylabel(r'$f(q)$') # y TeX plt.xlabel(r'$q$') # x TeX plt.grid(True) # plt.plot(q,f(q)) # plt.figure() plt.title(r'$y=h(q)$') # TeX plt.ylabel(r'$h(q)$') # y TeX plt.xlabel(r'$q$') # x TeX plt.grid(True) # plt.plot(q,h(q)) # plt.show() #
販売された商品の量に対する価格の依存性のグラフ
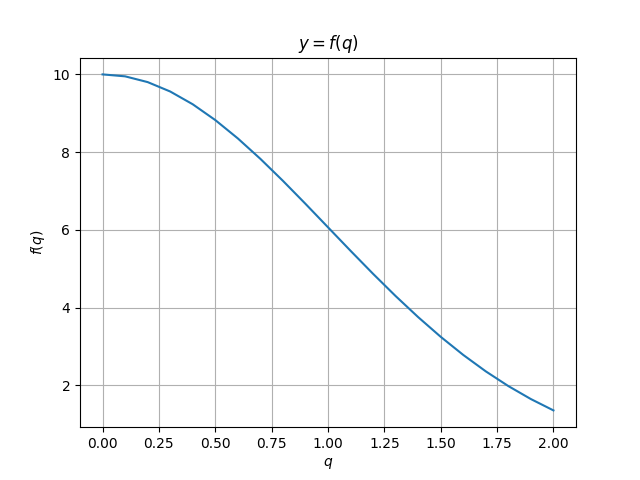
販売された商品の量に対するコストの依存関係のグラフ
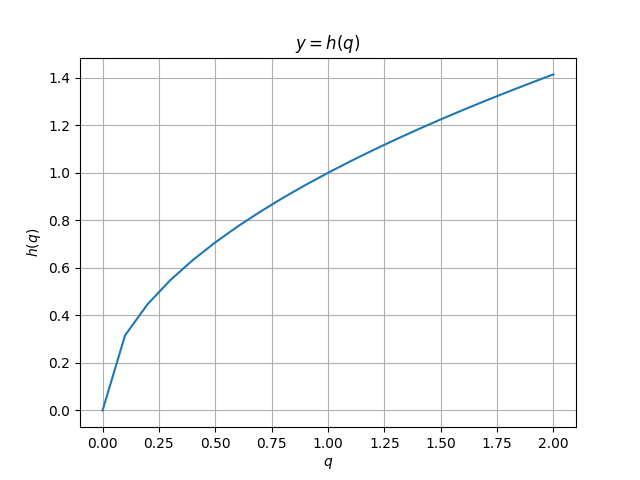
提供される商品の価格は、販売される商品の量の減少関数f(q)q = x + yによって特徴付けられます。 生産コストのコストは両方の企業で同じであり、増加関数h1(x)= h2(x)= h(x)を表します。
市場で競合する2つの企業の行動特性
上記の条件では、各会社の利益は次の機能によって決定されます。
L1(x、y)= x * f(x + y)-h(x)L2(x、y)= y * f(x + y)-h(y)
ゲーム理論の観点から、競合他社のさまざまな行動を考慮してください。
A. 最初のプレイヤーが勝利するゼロサムゲームがあるとします。
L1(x、y)= x * f(x + y)-h(x)
2番目のプレーヤーの目標は、最初の会社の破滅に対する利益を最小限にすることです。 見つける必要がある:
maxmin L(x、y)= maxmin x * f(x + y)-h(x)
xyxy
ゲームをマトリックス1に減らし、両方のプレイヤーの戦略を離散形式で表します: xi = i * x1、yj = j * h2、i、j = 0..N その解決策を次のリストに示します。
プログラムリスト-行動戦略A
# -*- coding: utf8 -*- import pylab from mpl_toolkits.mplot3d import Axes3D import numpy as np xmax=1;ymax=1;N=20; h1=xmax/N;h2=ymax/N# def L1(x,y):# return 10*x*np.e**(-0.5*(x+y)**2)-np.sqrt(x) def L2(x,y):# return 10*y*np.e**(-0.5*(x+y)**2)-np.sqrt(y) def fi(a,b):# for w in range(0,len(a)+1): if a[w]==b: return w L= np.zeros([N+1,N+1])# for i in range(0,N+1): for j in range(0,N+1): L[i,j]=L1(i*h1,j*h2) A=[];e=[] rows, cols = L.shape for i in range(rows): e=[] for j in range(cols): e.append(L[i,j]) A.append(min(e)) a=max(A);ia=fi(A,a);xa=ia*h1# B=[];e=[] rows, cols = L.shape for j in range(cols): e=[] for i in range(rows): e.append(L[i,j]) B.append(max(e)) b=min(B);ib=fi(B,b);yb=ib*h2# p1=round(L1(xa,yb),3) print(" -"+str(p1)) p2=round(L2(xa,yb),3) print(" -"+str(p2)) def makeData_L1 ():# - z, - x,y x=[h1*i for i in np.arange(0,N+1)] y=[h2*i for i in np.arange(0,N+1)] x,y= np.meshgrid(x, y) z=[] for i in range(0,N+1): z.append(L1(x[i],y[i])) return x, y, z fig = pylab.figure() axes = Axes3D(fig) x, y, z = makeData_L1() axes.plot_surface(x, y, z) def makeData_L2 ():# - z - x,y x=[h1*i for i in np.arange(0,N+1)] y=[h2*i for i in np.arange(0,N+1)] x,y= np.meshgrid(x, y) z=[] for i in range(0,N+1): z.append(L2(x[i],y[i])) return x, y, z fig = pylab.figure() axes = Axes3D(fig) x, y, z = makeData_L2() axes.plot_surface(x, y, z) pylab.show()
プログラムの結果:
最初の会社の利益-0.916
2番目の会社の利益-2.247
利益面-z、購入量-最初の会社のx、y
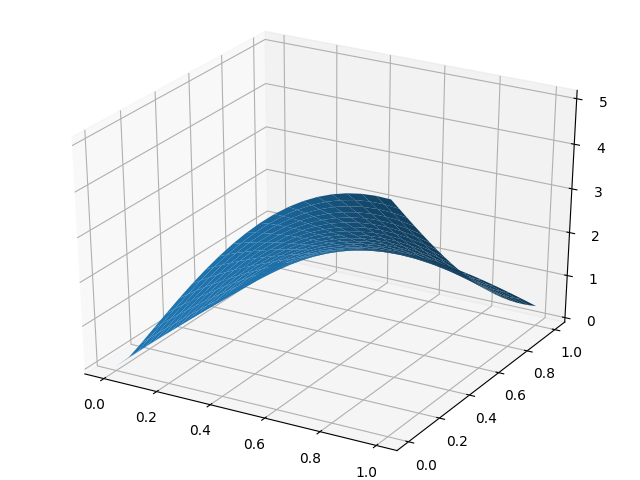
利益面-z、購入量-2番目の会社のx、y
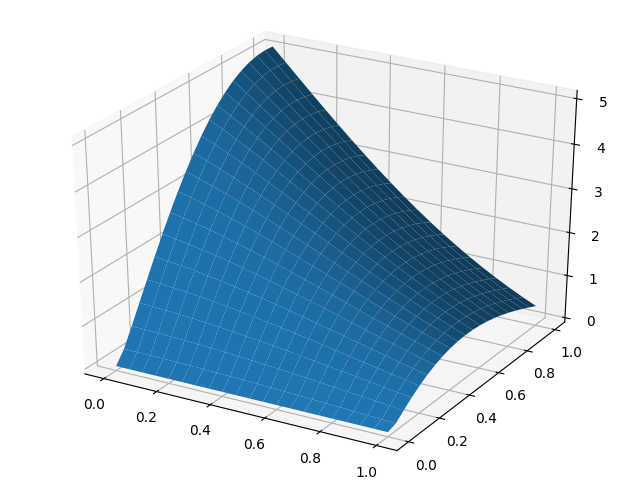
この決定に従って、価格を下げて最初のプレーヤーの利益を最小化するために、2番目のプレーヤーは最大の売上を維持する必要があります。 最初のプレーヤーはこれらの条件下で最適な生産量を見つけますが、2番目のプレーヤーよりも少ない利益を受け取ります。
B. 最初のプレーヤーがこの状況に慣れていない場合は、2番目のプレーヤーを台無しにする目標を設定することもできます。 それらが場所を変更する場合、機能の対称性により、最初のプレイヤーの最適な戦略は2番目のプレイヤーにとって最適になり、逆もまた同様です。 誰もが競合他社を台無しにしたい場合、彼は彼の製品の出力を最大化しなければなりません。
プログラムリスト-行動戦略B
# -*- coding: utf8 -*- import pylab import numpy as np xmax=1;ymax=1;N=20; h1=xmax/N;h2=ymax/N def L1(x,y): return 10*x*np.e**(-0.5*(x+y)**2)-np.sqrt(x) print(" -"+str(round(L1(xmax,ymax),3)))
プログラムの結果
-0.353の戦略を持つそれぞれの利益
戦略Bでは、各市場参加者はL1 = 0.353の利益を受け取ります。これは、各プレーヤーの場合、ケースAの場合よりも少なくなります。
C. 競合他社が市場区分に同意できる場合、次のPythonプログラムリストに示すように、 2,236ユニットの利益で各競合他社に対して最も収益性の高い結果を達成できます。
プログラムリスト-C行動戦略
# -*- coding: utf8 -*- import matplotlib.pyplot as plt import numpy as np xmax=1;ymax=1;N=20; h1=xmax/N;h2=ymax/N def L1(x,y): return 10*x*np.e**(-0.5*(x+y)**2)-np.sqrt(x) z=[L1(i*h1,i*h1)for i in np.arange(0,N+1)] x=[h1*i for i in np.arange(0,N+1)] xopt=x[z.index(max(z))] print(" -"+str(xopt)) print(" -"+str(round(max(z),3))) plt.title(' ') plt.grid(True) plt.plot(x,z) plt.show()
プログラムの結果:
-0.45を達成した各企業の商品の量
各社の利益-2.331

おわりに
戦略ゲームでは、操作側はそれ自体が最も不利なケースに依存するため、ミニマックスおよびマキシミン操作の計算になります。 このアプローチをPythonで実装すると、経済システムの最適化の分野に関連するゲームの問題を作成する可能性が広がります。
ご清聴ありがとうございました!
参照資料
1. 経済システムの最適化。 mathcad環境での例とアルゴリズム。