問題の声明
テキストのセマンティック(セマンティック)分析は、自然言語処理(NLP)に関連する人工知能システムの作成理論とコンピューター言語学の両方の重要な問題の1つです。 セマンティック分析の結果を使用して、たとえば精神医学(患者の診断)、政治学(選挙結果の予測)、貿易(この製品に関するコメントに基づく特定の製品の需要の分析)、哲学(著作権テキストの分析など)の問題を解決できます。 )、検索エンジン、自動翻訳システム。 Google検索エンジンは完全にセマンティック分析に基づいています。
セマンティック分析の結果の視覚化は、分析結果に基づいて迅速かつ効果的な意思決定を提供できるため、実装の重要な段階です。
ネットワーク内の潜在意味解析(LSA)の出版物の分析では、分析結果の視覚化は、単語と文書の座標をプロットした意味空間の2つの座標グラフの形式で2つの出版物[1,2]でのみ行われます。 このような視覚化では、関連するドキュメントのグループを明確に識別し、ドキュメントに属する単語に従ってそれらのセマンティック接続のレベルを評価することはできません。 「Pythonツールを使用した完全な潜在意味解析」[1]というタイトルの私の出版物では、潜在意味解析結果のクラスター解析を使用しようとしましたが、クラスターラベルと重心座標のみが視覚化なしで単語とドキュメントのグループに対して決定されました。
クラスター分析によるLSA結果の視覚化
以下は、クラスタリングによる結果の視覚化を含むLSAのすべての手順です。
- ストップワードは、分析されたドキュメントから除外されます。 これらはすべてのテキストに見られる単語であり、セマンティックロードを持ちません。これらはまず第一に、すべての接続詞、助詞、前置詞、その他多くの単語です。
- 分析された文書から、数字、個々の文字、句読点を除外する必要があります。
- すべての文書に一度だけ現れる単語を除外します。 これは最終結果には影響しませんが、数学的計算を大幅に簡素化します。
- 文書のすべての単語を使用して、ステミング操作を実行する必要があります-単語の基礎を取得します。
- インデックス付きフィッシングの頻度行列を作成します。 このマトリックスでは、行はインデックス付きの単語に対応し、列はドキュメントに対応します。 マトリックスの各セルには、対応するドキュメントに単語が何回現れるかを示す必要があります。
- 結果の周波数行列を正規化する必要があります。 TF-IDFマトリックスを正規化するための標準的な方法[3]。
- 次のステップは、結果の行列の特異分解です。 特異分解[4]; マトリックスを3つのコンポーネントに分解する数学演算です。 すなわち 次の形式で元の行列Mを表します。
M = U * W * V ^ t
ここで、UとV ^ tは直交行列で、Wは対角行列です。 さらに、行列Wの対角要素は降順に並べられます。 行列Wの対角要素は、特異数と呼ばれます。 - 行列Uの最後の列と行列V ^ tの最後の行を破棄し、最初の2だけを残します。これらは、それぞれ、行列Uの各単語のX、Y座標と、行列V ^ tの各ドキュメントのX、Y座標です。 この形式の分解は、2次元特異分解と呼ばれます。
- 行列Uの最後の列と行列V ^ tの最後の行を破棄し、最初の3のみを残します。これらは、行列Uの各単語の座標X、Y、Zおよび行列V ^ tの各ドキュメントの座標X、Y、Zです。 この種の分解は、3次元特異分解と呼ばれます。
- マトリックスUワードの2列とマトリックスV ^ t文書の2行の座標X、Yのネストされたリストの形式での初期データの準備。
- 行列Uの2列の行と行列V ^ tの2行の列の間のユークリッド距離のグラフ化。
- クラスター数の分離[5,6,7]。
- ダイアグラムと樹状図の作成。
- マトリックスUワードの3列とマトリックスV ^ tドキュメントの3行の座標X、Y、Zのネストされたリストの形式での初期データの準備。
- クラスター数の割り当て。
- ダイアグラムと樹状図の作成。
- 単語および文書の正規化された周波数行列の2次元および3次元特異分解のクラスター分析の結果の比較。
上記の手順を実装するために、特別なプログラムが開発されました。このプログラムでは、出版物[2]と同じドキュメントのテストセットが比較に使用されました。
LSA結果視覚化ソフトウェア
プログラムの結果
直交行列Uワードの最初の2列
wikileaks [-0.0741 0.0991]
逮捕[-0.023 0.0592]
イギリス[-0.023 0.0592]
手渡し[-0.0582 -0.5008]
ノーベルの[-0.0582 -0.5008]
創設者[-0.0804 0.1143]
警察官[-0.0337 0.0846]
prem [-0.0582 -0.5008]
prot [-0.5954 0.0695]
国[-0.3261 -0.169]
裁判所[-0.3965 0.1488]
アメリカ合衆国[-0.5954 0.0695]
式典[-0.055 -0.3875]
Vtドキュメントの直交行列の最初の2行
[[0.0513 0.6952 0.1338 0.045 0.0596 0.2102 0.6644 0.0426 0.0566]
[-0.1038 -0.1495 0.5166 -0.0913 0.5742 -0.1371 0.0155 -0.0987 0.5773]]
Uワードの直交行列の最初の3列
wikileaks [-0.0741 0.0991 -0.4372]
逮捕[-0.023 0.0592 -0.3241]
イギリス[-0.023 0.0592 -0.3241]
手渡し[-0.0582 -0.5008 -0.1117]
ノーベルの[-0.0582 -0.5008 -0.1117]
創設者[-0.0804 0.1143 -0.5185]
警察官[-0.0337 0.0846 -0.4596]
prem [-0.0582 -0.5008 -0.1117]
prot [-0.5954 0.0695 0.1414]
国[-0.3261 -0.169 0.0815]
裁判所[-0.3965 0.1488 -0.1678]
アメリカ合衆国[-0.5954 0.0695 0.1414]
式典[-0.055 -0.3875 -0.0802]
Vtドキュメントの直交行列の最初の3行
[[0.0513 0.6952 0.1338 0.045 0.0596 0.2102 0.6644 0.0426 0.0566]
[-0.1038 -0.1495 0.5166 -0.0913 0.5742 -0.1371 0.0155 -0.0987 0.5773]
[0.5299 -0.0625 0.0797 0.4675 0.1314 0.3714 -0.1979 0.5271 0.1347]]
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy from numpy import * import nltk import scipy from nltk.corpus import brown from nltk.stem import SnowballStemmer from scipy.spatial.distance import pdist from scipy.cluster import hierarchy import matplotlib.pyplot as plt stemmer = SnowballStemmer('russian') stopwords=nltk.corpus.stopwords.words('russian') # docs =[ " WikiLeaks",# № 0 " , ",# №1 " 19 ",# №2 " Wikileaks ",# №3 " ",# №4 " Wikileaks",# №5 " ",# №6 " WikiLeaks, , ",# №7 " "# №8 ] word=nltk.word_tokenize((' ').join(docs))# n=[stemmer.stem(w).lower() for w in word if len(w) >1 and w.isalpha()]# stopword=[stemmer.stem(w).lower() for w in stopwords]# - fdist=nltk.FreqDist(n) t=fdist.hapaxes()# # d={};c=[] for i in range(0,len(docs)): word=nltk.word_tokenize(docs[i]) word_stem=[stemmer.stem(w).lower() for w in word if len(w)>1 and w.isalpha()] word_stop=[ w for w in word_stem if w not in stopword] words=[ w for w in word_stop if w not in t] for w in words: if w not in c: c.append(w) d[w]= [i] elif w in c: d[w]= d[w]+[i] a=len(c); b=len(docs) A = numpy.zeros([a,b]) c.sort() for i, k in enumerate(c): for j in d[k]: A[i,j] += 1 # TF-IDF wpd = sum(A, axis=0) dpw= sum(asarray(A > 0,'i'), axis=1) rows, cols = A.shape for i in range(rows): for j in range(cols): m=float(A[i,j])/wpd[j] n=log(float(cols) /dpw[i]) A[i,j] =round(n*m,2) # U, S,Vt = numpy.linalg.svd(A) rows, cols = U.shape for j in range(0,cols): for i in range(0,rows): U[i,j]=round(U[i,j],4) print(' 2 U ') for i, row in enumerate(U): print(c[i], row[0:2]) res1=-1*U[:,0:1]; res2=-1*U[:,1:2] data_word=[] for i in range(0,len(c)):# data_word.append([res1[i][0],res2[i][0]]) plt.figure() plt.subplot(221) dist = pdist(data_word, 'euclidean')# ( ) plt.hist(dist, 500, color='green', alpha=0.5)# Z = hierarchy.linkage(dist, method='average')# plt.subplot(222) hierarchy.dendrogram(Z, labels=c, color_threshold=.25, leaf_font_size=8, count_sort=True,orientation='right') print(' 2 Vt ') rows, cols = Vt.shape for j in range(0,cols): for i in range(0,rows): Vt[i,j]=round(Vt[i,j],4) print(-1*Vt[0:2, :]) res3=(-1*Vt[0:1, :]);res4=(-1*Vt[1:2, :]) data_docs=[];name_docs=[] for i in range(0,len(docs)): name_docs.append(str(i)) data_docs.append([res3[0][i],res4[0][i]]) plt.subplot(223) dist = pdist(data_docs, 'euclidean') plt.hist(dist, 500, color='green', alpha=0.5) Z = hierarchy.linkage(dist, method='average') plt.subplot(224) hierarchy.dendrogram(Z, labels=name_docs, color_threshold=.25, leaf_font_size=8, count_sort=True) #plt.show() print(' 3 U ') for i, row in enumerate(U): print(c[i], row[0:3]) res1=-1*U[:,0:1]; res2=-1*U[:,1:2];res3=-1*U[:,2:3] data_word_xyz=[] for i in range(0,len(c)): data_word_xyz.append([res1[i][0],res2[i][0],res3[i][0]]) plt.figure() plt.subplot(221) dist = pdist(data_word_xyz, 'euclidean')# ( ) plt.hist(dist, 500, color='green', alpha=0.5)# Z = hierarchy.linkage(dist, method='average')# plt.subplot(222) hierarchy.dendrogram(Z, labels=c, color_threshold=.25, leaf_font_size=8, count_sort=True,orientation='right') print(' 3 Vt ') rows, cols = Vt.shape for j in range(0,cols): for i in range(0,rows): Vt[i,j]=round(Vt[i,j],4) print(-1*Vt[0:3, :]) res3=(-1*Vt[0:1, :]);res4=(-1*Vt[1:2, :]);res5=(-1*Vt[2:3, :]) data_docs_xyz=[];name_docs_xyz=[] for i in range(0,len(docs)): name_docs_xyz.append(str(i)) data_docs_xyz.append([res3[0][i],res4[0][i],res5[0][i]]) plt.subplot(223) dist = pdist(data_docs_xyz, 'euclidean') plt.hist(dist, 500, color='green', alpha=0.5) Z = hierarchy.linkage(dist, method='average') plt.subplot(224) hierarchy.dendrogram(Z, labels=name_docs_xyz, color_threshold=.25, leaf_font_size=8, count_sort=True) plt.show()
プログラムの結果
直交行列Uワードの最初の2列
wikileaks [-0.0741 0.0991]
逮捕[-0.023 0.0592]
イギリス[-0.023 0.0592]
手渡し[-0.0582 -0.5008]
ノーベルの[-0.0582 -0.5008]
創設者[-0.0804 0.1143]
警察官[-0.0337 0.0846]
prem [-0.0582 -0.5008]
prot [-0.5954 0.0695]
国[-0.3261 -0.169]
裁判所[-0.3965 0.1488]
アメリカ合衆国[-0.5954 0.0695]
式典[-0.055 -0.3875]
Vtドキュメントの直交行列の最初の2行
[[0.0513 0.6952 0.1338 0.045 0.0596 0.2102 0.6644 0.0426 0.0566]
[-0.1038 -0.1495 0.5166 -0.0913 0.5742 -0.1371 0.0155 -0.0987 0.5773]]
Uワードの直交行列の最初の3列
wikileaks [-0.0741 0.0991 -0.4372]
逮捕[-0.023 0.0592 -0.3241]
イギリス[-0.023 0.0592 -0.3241]
手渡し[-0.0582 -0.5008 -0.1117]
ノーベルの[-0.0582 -0.5008 -0.1117]
創設者[-0.0804 0.1143 -0.5185]
警察官[-0.0337 0.0846 -0.4596]
prem [-0.0582 -0.5008 -0.1117]
prot [-0.5954 0.0695 0.1414]
国[-0.3261 -0.169 0.0815]
裁判所[-0.3965 0.1488 -0.1678]
アメリカ合衆国[-0.5954 0.0695 0.1414]
式典[-0.055 -0.3875 -0.0802]
Vtドキュメントの直交行列の最初の3行
[[0.0513 0.6952 0.1338 0.045 0.0596 0.2102 0.6644 0.0426 0.0566]
[-0.1038 -0.1495 0.5166 -0.0913 0.5742 -0.1371 0.0155 -0.0987 0.5773]
[0.5299 -0.0625 0.0797 0.4675 0.1314 0.3714 -0.1979 0.5271 0.1347]]
単語と文書の正規化された周波数行列の2次元特異分解の図と樹状図。
ドキュメントの近接性(ドキュメントを参照)とドキュメントへの単語の帰属を明確に視覚化しました。
単語と文書の正規化された周波数行列の3次元特異分解の図と樹状図。
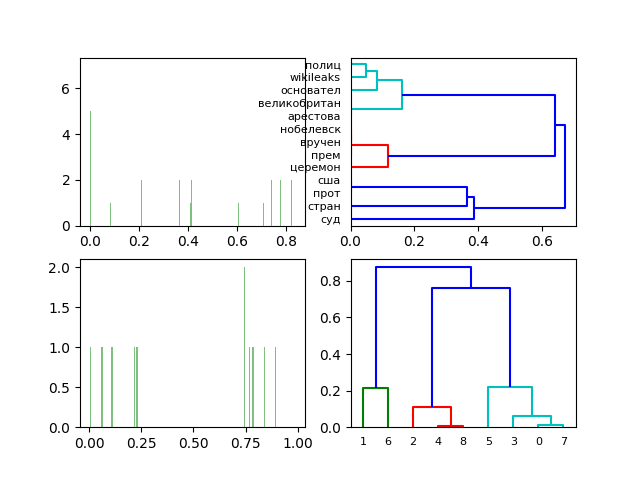
指定されたドキュメントセット(ドキュメントを参照)の単語とドキュメントの正規化された頻度行列の3次元特異分解への移行は、LSA分析の結果を定性的に変更しません。
結論
私の意見では、与えられたLSA視覚化手法はLSA自体への追加に成功し、開発者の注目に値します。
ご清聴ありがとうございました!