対数これ：機械学習における対数微分法

問題の手法-対数微分の方法-は、対数微分の基本特性を使用してあらゆる種類のことを行うのに役立ちます。 この方法は、 以前に調査した確率的最適化問題を解くのに最適であることが証明されています。 そのアプリケーションのおかげで、確率的勾配推定値を取得する新しい方法を発見しました。 評価関数を決定するためにトリックを使用する例から始めましょう。



かなり数学的です。

スコア関数

対数微分法は、関数p（x;θ） の対数のパラメーターθへの勾配の規則の適用です。

$$ $$表示$$∇θlog p（x;θ）=∇θp（x;θ）/ p（x;θ）$$表示$$

この方法の適用は、関数p（x;θ）が尤度関数である場合に成功することがわかります 。つまり、パラメーターθを持つ関数fは確率変数xの確率を表します。 この特定のケースでは、関数

$$

$$∇θlogp（x;θ）$$

はevaluativeと呼ばれ、右側は評価の比率です。 評価関数には、いくつかの有用なプロパティがあります。



最尤法を評価するための主な操作 。 最尤法は、 一般化線形回帰 、 深層学習 、 核機械 、次元削減、 テンソル分解などで使用される機械学習の主要な原理の1つです。 これらすべての問題を解決するには評価が必要です。



スコアのペアレント化はゼロです。 対数微分法の最初の使用法は次のとおりです。







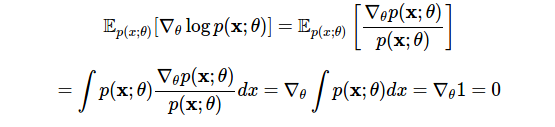
1行目では、導出された対数を使用し、2行目では、微分と統合の順序を変更しました。 この恒等式により、必要な確率的柔軟性のタイプが明らかになります：期待値がゼロの推定値から任意の項を差し引くことができ、変更は期待される結果に影響しません（詳細：制御変数を参照）。



推定分散は、Cramer-Raoの下限を決定するために使用されるフィッシャー情報です。







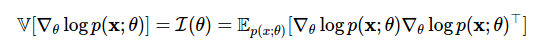
これで、対数確率の勾配から確率の勾配へ、またはその逆に1つの境界線内を移動できます。 ただし、今日の投稿の主な悪人である方法4からの予想される複雑な勾配が再び現れます。 新しい機能（評価関数）を使用して、このクラスの問題に対する別のスマート評価ソリューションを見つけることができます。

評価機能評価ユニット

私たちの仕事は、関数fの数学的期待勾配を計算することです：







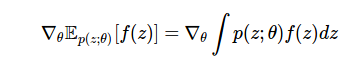
これは、頻繁に遭遇する機械学習のタスクであり、 変分推論 、値の関数、および強化を伴う学習プロセスでの政治家（戦略）のトレーニング、 金融工学のデリバティブの価格設定、オペレーションズリサーチの在庫会計などの後続の計算に必要です。



積分は通常未知であり、勾配を計算するパラメーターθの分布はp（z;θ）であるため、この勾配を計算することは困難です。 さらに、微分不可能な関数についてこの勾配を計算する必要があるかもしれません。 対数微分の方法と推定関数の特性を使用して、この勾配をより便利な方法で計算できます。







この式を導出し、最適化問題に対するその結果を考慮します。 この目的のために、頻繁に出会う別の方法-確率的同一性の方法を使用します。この方法では、式に1を掛けます-確率密度をそれ自体で割った数です。 この方法を対数微分法と組み合わせて、推定勾配関数を推定するためのブロックを取得します。







これらの4行では、多くの操作を実行しました。 最初の行では、導関数を積分に置き換えました。 2番目の方法では、確率論的な方法を適用して、推定係数を作成しました。 対数微分を使用して、この係数を3行目の対数確率の勾配に置き換えました。 これにより、 モンテカルロ法を使用して計算した4番目の行の目的の確率的推定値が得られます。最初にp（z）からサンプルを取得し、次に重み付き勾配項を計算します。



これは不偏勾配推定です。 このプロセスでの仮定は単純でした：

• 微分による統合の置き換えは有効です。 一般的な用語で示すことは困難ですが、通常、置換自体は問題を引き起こしません。 ここで与えられたライプニッツの式と分析を参照することにより、この手法の正確性を確認できます[ 1 ]。
• 関数f（z）は微分可能であってはなりません。 したがって、それを評価したり、特定のzの値の変化を観察したりできます。
• 分布p（z）からサンプルを取得することは難しくありません。モンテカルロ法で積分を推定する必要があるからです。

他の多くのトリックのように、ここで選択したパスは他の多くの研究分野ですでにカバーされており、各領域にはすでに独自の用語、方法の開発の歴史、問題の定式化に関連する一連のタスクがあります。 以下に例を示します。



1. スコア関数推定器



結論により、期待度勾配を評価関数の期待度に変換することができました

$$

$$∇θlogp（z;θ）、$$

これにより、そのような推定値を評価関数のブロックとして指定するのに便利です[ 2 ]。 これはかなり一般的な用語であり、使用することを好みます。



このトピックに関する多くの洞察に富んだ観察と歴史的に重要な多くの開発は、「 推定関数法によるコンピューターシミュレーションモデルの感度の最適化と分析 」という題名の論文で紹介されています。



2. 信頼性比の方法



このクラスの評価の主な普及者の1つはP.V. グリン [ 3 ]。 彼は評価の割合を解釈します

$$ $$表示$$∇θp（z;θ）/ p（z;θ）$$表示$$

尤度比として、評価のブロックを尤度比の方法として説明します。 これは、「尤度比」という用語のやや非標準的な使用法だと思います。 通常、同じパラメーターを持つ異なる関数の比率ではなく、異なるパラメーターを持つ同じ関数の比率を表します。 したがって、「評価関数評価ユニット」という用語を好みます。



多くの著者、特にMichael Fu [ 4 ]は、尤度比と推定方法（LR / SF）について話しています。 トピックに関する最も重要な作品：「 確率システムの尤度係数の推定比 」、ここでGlynnは分散の最も重要な特性を詳細に説明し、Michael Fu 勾配推定を行います。



3. 自動化された変分出力



変分微分は、 ベイジアン解析で発生する難解な積分を確率的最適化の問題に変換します。 この分野に、異なる用語で知られている評価関数を評価するためのブロックもあることは驚くことではありません。



4. 戦略の報酬と勾配



強化学習の問題を解決するために、関数fを環境から受け取った報酬と比較し、分布p（z;θ）をポリシーと比較し、推定値をポリシーの勾配、または場合によっては特徴的な可能性と比較することができます。



直観的に、これは次のように説明できます。高い報酬に対応するポリシーの勾配は、評価ユニットからの強化により大きな重みを受け取ります。 したがって、評価単位はREINFORCE [ 5 ]と呼ばれ、この一般化は現在、戦略（ポリシー）の勾配定理を形成しています。

制御変数

このモンテカルロ推定を効率的に実行するには、分散を可能な限り小さくする必要があります。 それ以外の場合、グラデーションは役に立ちません。 変更された推定値を使用することで、より多くの分散制御を実現できます。







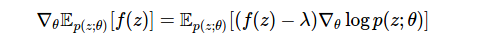
ここで、新しい項λは制御変数と呼ばれ、モンテカルロ推定値の分散を減らすために広く使用されています。 制御変数は、平均値がゼロのスコアに追加される追加の用語です。 このような変数は、予想に影響を与えないため、どの段階でも入力できます。 制御変数は分散に影響します。 推定値を使用する際の主な問題は、制御変数の選択です。 最も簡単な方法は定数パラメーターを使用することですが、他の方法もあります：合理的なサンプリングスキーム（たとえば、 アンチセティックまたは成層 ）、デルタメソッド、または適応定数パラメーター。 分散源と分散低減方法に関する最も包括的な議論の1つは、 P。Glassermanによる本書で提供されています [ 6 ]

確率的評価システムのグループ

今日の推定値を、 方法4で線形微分法を使用して導出した推定値と比較します。







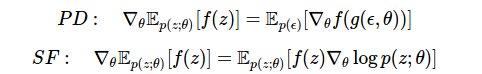
ここには、2つの効果的なアプローチがあります。 できること：

• 関数が微分可能である場合、線形微分を使用して関数fを微分します。または
• 推定関数を使用して密度p（z）を微分します。

確率的勾配推定を作成する方法は他にもありますが、これら2つが最も一般的です。 これらは簡単に組み合わせることができるため、計算のさまざまな段階で最適な推定値（最小の分散を提供）を使用できます。 この問題は、特に確率的計算グラフを使用することで解決できます 。

おわりに

対数微分法により、正規化された確率分布と対数確率分布を交互に切り替えることができます。 これは、推定関数を決定するための基礎を形成し、統計的知識のほとんどを形成したもっともらしい推定および重要な漸近解析の方法として機能します。 この方法は、現在直面している多くの重要な機械学習問題の根底にある確率的最適化問題を解く際に汎用勾配を推定するために使用できることに注意することが重要です。 モンテカルロ勾配推定は、私たちが目指している真に普遍的な機械学習に必要です。 このためには、そのような評価の根底にあるパターンと方法を理解することが重要です。

---