
SAプラス-比較的高速なアルゴリズム速度、実装の容易さ。 マイナスのうち、アルゴリズムは「柔軟」ではなく、いわゆる「フィギュアを再構築する能力」もありません。 シミュレーションアニーリングアルゴリズムの本質を理解したい方は、この記事を参照してください 。
AS(ACS)の長所は、集団主義の存在、反復から反復へのアルゴリズムの収束、図を再構築する機能(実際には、常に最適なパラメーターを選択して、最適なローカル選択でスタックしない代替方法を探すこと)、部分並列性の可能性です。 マイナス-アルゴリズム時間が長く、頂点の数が多い複雑さ。 蟻のアルゴリズムの本質を理解したい人のために、私はサイトを参照します 。 また、以前の記事でMatLabで記述されたコードを見ることができます。そこには、原則を理解できるコメントがあります。
今日は、アルゴリズムの最初のバージョンを紹介します。これは、さまざまなアルゴリズムの最高のものを組み込んでおり、最初の試行で、通常のホームPCで5秒以内に100頂点へのグローバル最適パスを高い確率で見つけることができます。 グラフィックイラストを使用した例を使用して、すべてを表示しようとします。 コードはMatLabで書かれています。 彼の要素のいくつかの場所で-ベクトル、誰かがアルゴリズムを彼らの言語に移すのに問題があるなら-コメントに書いてください。 もっと真剣に興味を持っている人、またはバージョンを実装したい人のために-前回の記事をご覧になることと、記事の最後に添付される完全なアルゴリズムコードをご覧になることをお勧めします。 コメントのすべての行をペイントしようとしました。
おそらく、このアルゴリズムは既に存在しているかもしれませんが、グローバルネットワークの広大さにはそれが見つかりませんでした。 したがって、この記事の実装では何をすべきでしょうか:
1-可能な限りシンプル
2-可能な限り高速
3-CPU(現在ファッショナブルなGPUを含む)を並列化する機能
4-柔軟(近代化の可能性、パラメーターの可変性)
5-ランダムパラメーターへの依存度が低い
6-フィギュアを再構築する可能性
私が図を再構築するという意味では、以下を参照してください。
Eil101タスク(巡回セールスマンの問題)でTSP図を再構築します。
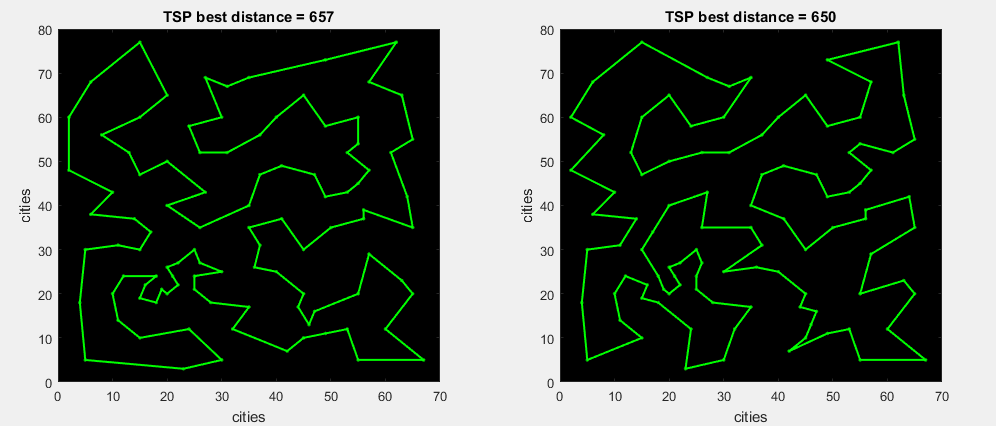
この画像は、両方のルートの距離が1%異なることを示していますが、ルートは完全に異なっています。 つまり、まったく異なる数字です。 適切なアルゴリズムは、これらの形状をできるだけ多く作成する必要があります。 SAでは未開発です。
初期の高温およびゆっくりと下降する温度でアニーリングをシミュレートする方法(以前の記事で見たように)は良い結果を達成できますが、これはアルゴリズムの時間を大幅に増加させ、グローバルな最良の方法を保証しません。 もう1つは、複数のSAアルゴリズムを一度に実行し、それぞれの結果を配列に入れて、最適なアルゴリズムを選択する場合です。
従来のSAアルゴリズムの欠点の1つは、「ランダム」な要素が多すぎて、最初に2つの頂点をランダムに選択し、次に「ランダム」に選択して最悪の決定を受け入れるかしないことです。 このアルゴリズムでは、ランダム性のシェアを最小化しようとしました。
したがって、このアルゴリズムでは、2つの頂点を「ランダム化」する代わりに、パスの反転のすべての可能な部分をすぐに調べます。 私たちの目標はグローバルな最適化のみであり、
明確化:
ルートがあります:[1,2,3,4,5,6,7,8]-旅行者は最初に最初の都市、次に2番目の都市などを訪問します。 「2つの頂点をランダム化する」とは、2つの数値(偶数の分布)をランダムに選択することを意味します。2と6の場合、それらの間のパスを逆にします。 パスの形式は次のとおりです:[1、6、5,4,3、2、8]。
入力としてルート(任意、最も不正確なものも含む)をとる関数のパス反転部分を徹底的に検索し、ターンのルートの最も収益性の高い部分を検索し、展開してから、以前の変更を考慮して、ルートの最も収益性の高い部分を再度検索し、サイクルを繰り返します、ルートの交換部品は距離を改善しません。
この方法は、2optアルゴリズムとして知られています。 ただし、従来の2optアルゴリズムでは、結果を改善するルートの一部をすぐに展開します。ここでは、標準の2optに加えて、「より良い置換」を探しています。
図解:
最初のgifアニメーションで、アルゴリズムはルートの見つかった部分をすぐに展開し、全体の距離を改善します(標準の2-opt)
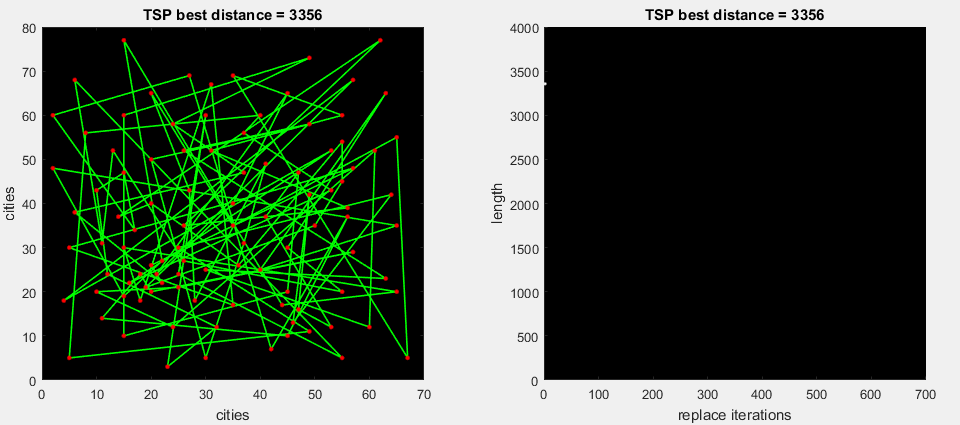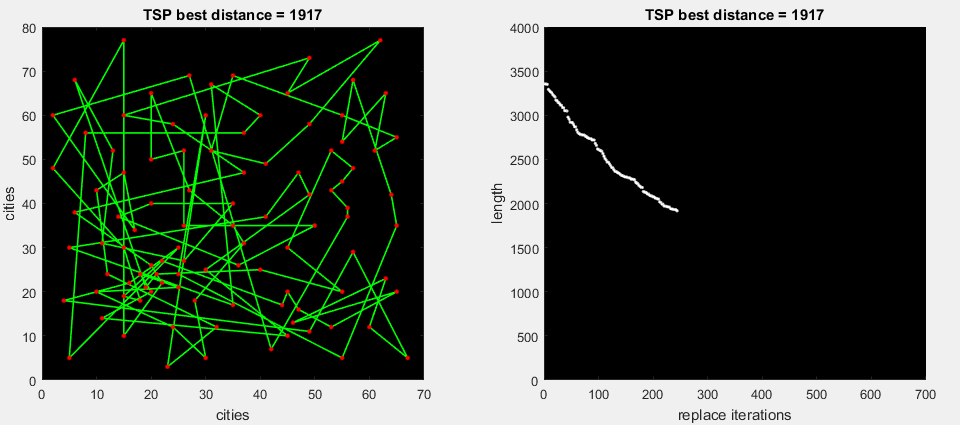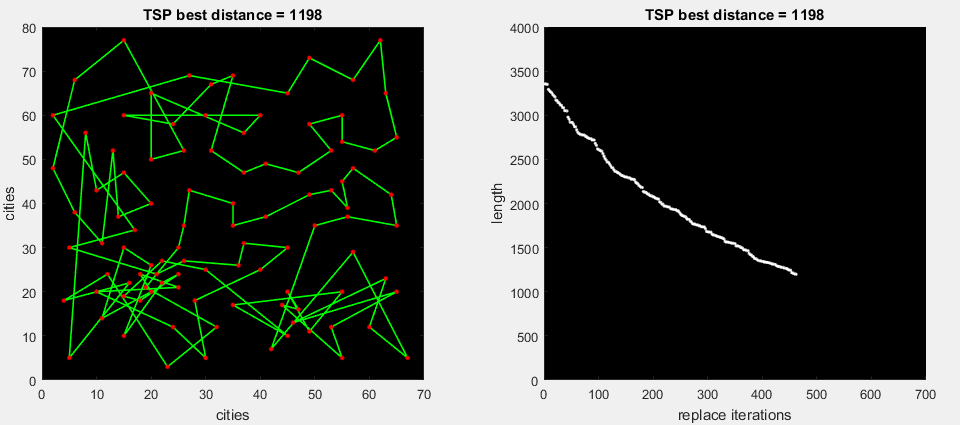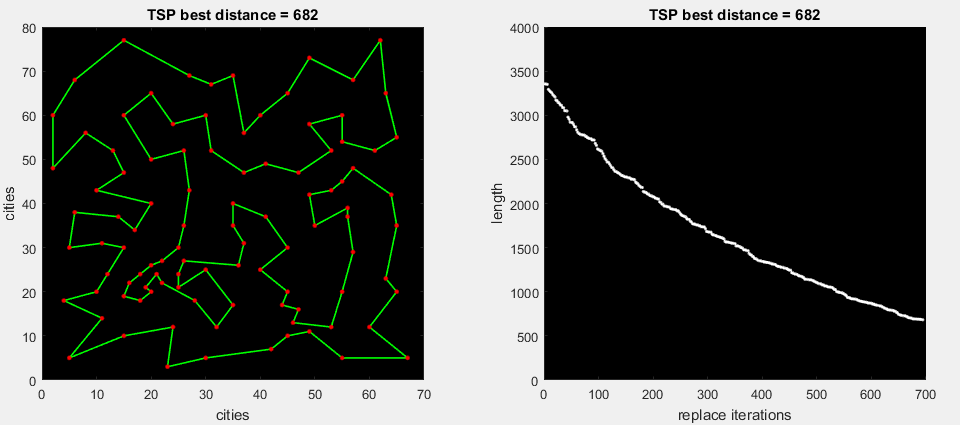
2番目のアニメーションgifで、アルゴリズムはルートの一部の可能なすべての置換を実行し、最大デルタ(m。2-opt)を展開します
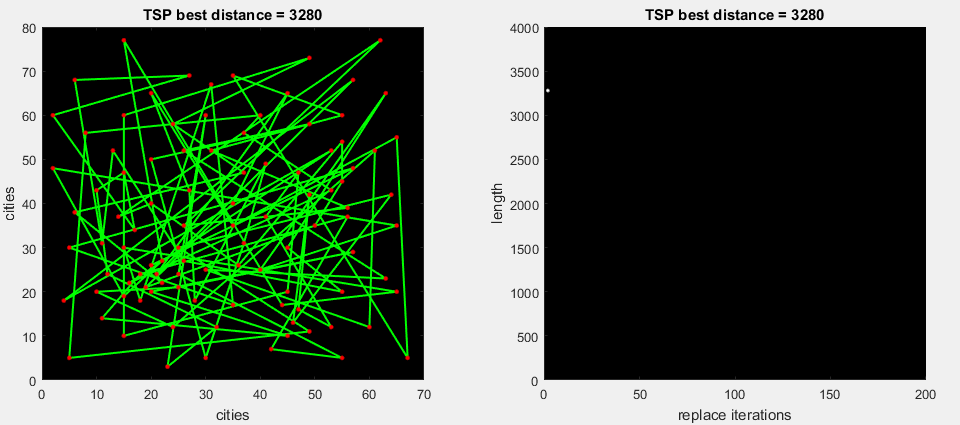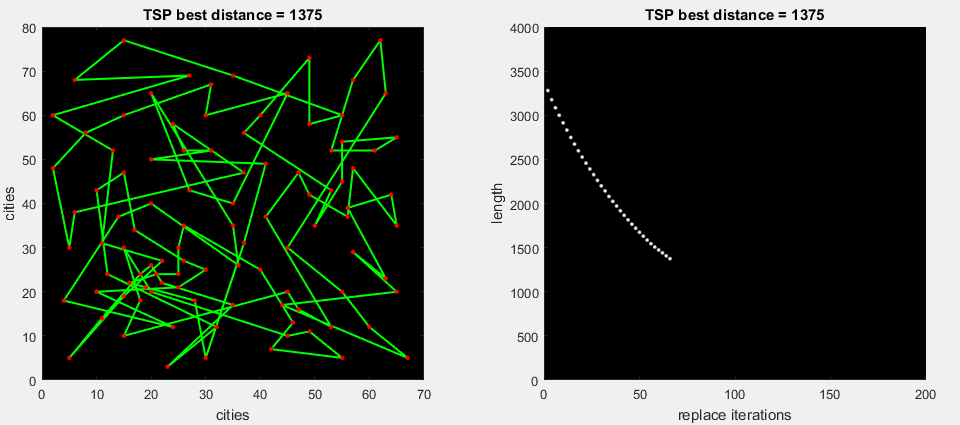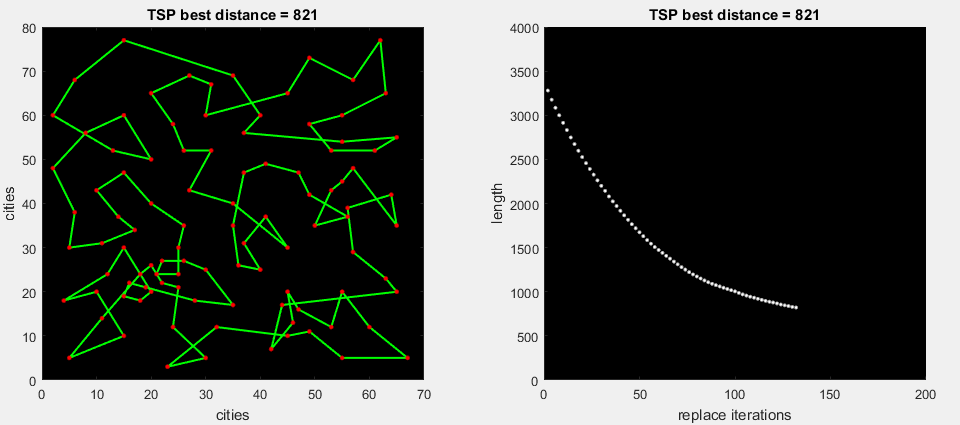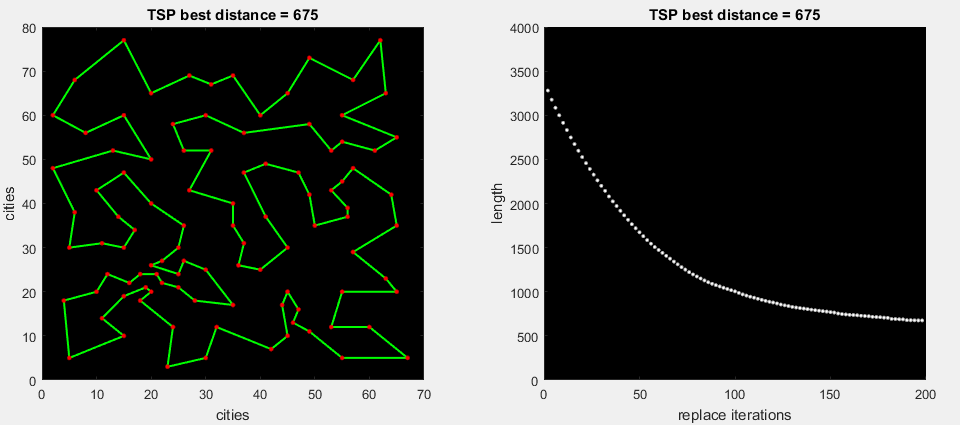
今日のアルゴリズムでは、一連のテストでより良い結果が示されるため、2番目のオプションを使用します。 最初のオプションは改訂のために残されます。
そのため、特定の「アニーリングをシミュレートする最新の方法」でルートを最適化する2つの関数があります。 並列ループ(MatLabeでparfor演算子を使用すると、PCのすべてのカーネルを使用できる)をこれらのルートの数千(これも並列ループで作成されます)の関数に渡し、最適なものを選択するだけです。
ブルートフォース機能(最適な代替)
% % ( ) % dist - % route - % openclose - %------------------------------------------------------------------------ function [tour, distance] = all_brute_best(dist,route,n) global_diff = -0.1; best_dist = inf; % , while global_diff < 0 global_diff = 0; p1 = route(n); % for i = 1:n-2 t1 = p1; p1 = route(i); t2 = route(i+1); spd_var = dist(t1,p1); for j = i+2:n p2 = t2; t2 = route(j); diff = (dist(t1,p2) - dist(p2,t2))... + (dist(p1,t2) - spd_var); % if global_diff > diff global_diff = diff; % "" imin = i; jmin = j; end end end % if global_diff < 0 route(imin:jmin-1) = route(jmin-1:-1:imin); end end %-------------------------------------------------------------------- % cur_dist = 0; for i = 1:n-1 cur_dist = cur_dist + dist(route(i),route(i+1)); end % cur_dist = cur_dist + dist(route(1),route(end)); %-------------------------------------------------------------------- % if cur_dist < best_dist best_route = route; best_dist = cur_dist; end % - distance = best_dist; % tour = best_route; end
検索機能(各置換)
% % ( ) % dist - % route - % openclose - %------------------------------------------------------------------------- function [tour, distance] = all_brute_first(dist,route,n) global_diff = -0.1; best_dist = inf; % , while global_diff < 0 global_diff = 0; p1 = route(n); % for i = 1:n-2 t1 = p1; p1 = route(i); t2 = route(i+1); spd_var = dist(t1,p1); for j = i+2:n p2 = t2; t2 = route(j); diff = (dist(t1,p2) - dist(p2,t2))... + (dist(p1,t2) - spd_var); % if diff < 0 global_diff = diff; % "" imin = i; jmin = j; break end end % if diff < 0 break end end % if global_diff < 0 route(imin:jmin-1) = route(jmin-1:-1:imin); end end %-------------------------------------------------------------------- % cur_dist = 0; for i = 1:n-1 cur_dist = cur_dist + dist(route(i),route(i+1)); end % cur_dist = cur_dist + dist(route(1),route(end)); %-------------------------------------------------------------------- % if cur_dist < best_dist best_route = route; best_dist = cur_dist; end % - distance = best_dist; % tour = best_route; end
ここからが楽しみです。
転送するルート 当然、離れるときは、可能な限り異なる数字を含める必要があります(上記参照)。 また、単純にランダムな配列を渡すと、グローバルに優れた結果は得られません。 それで、「all_brute_best」関数の入力へのルートの配列が異なるアルゴリズムで構成されるようにします。
すぐに頭に浮かんだのは、最も近い隣人の方法です 。 各都市を一度終了し、次元nxnルート(nは都市の数)の配列を取得します。 次に、この配列を最適化関数に渡します。
Matlabeでは、次のように最寄りの都市が訪問されます。
最近傍法
parfor k = 1:n % ( ) dist_temp = dist; % route = zeros(1,n); % next_point = start_route(k); % route(1) = next_point; % for e = 2:n % dist_temp(next_point,:) = nan; % [~,next_point] = min(dist_temp(:,next_point)); % route(e) = next_point; end % 1- if check_routes == true route = check_tour(route); end % arr_route_in(k,:) = route; end
一般に、TSP(巡回セールスマン問題)のタスクは多くの人によって解決されました。 また、最も「高度な」アルゴリズムによって解決されました。 そのため、これまでに見つかった最適なソリューションがサイトに配置されています 。
Eil76タスクのアルゴリズムを確認しましょう。その視覚的な作業を以下に示します。 見つかった最適なパスは538です。
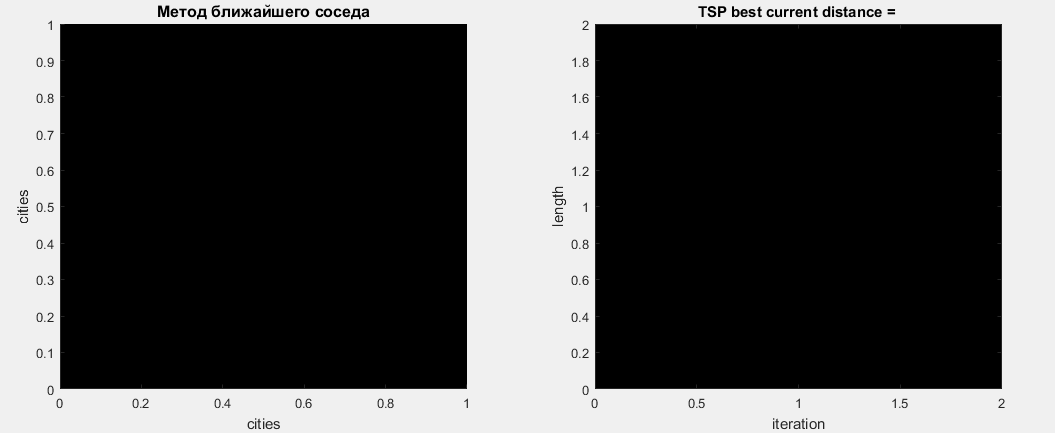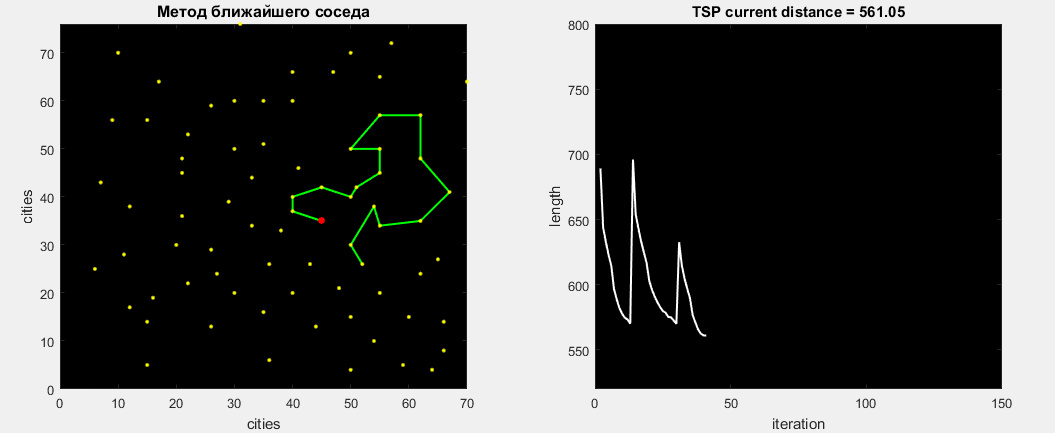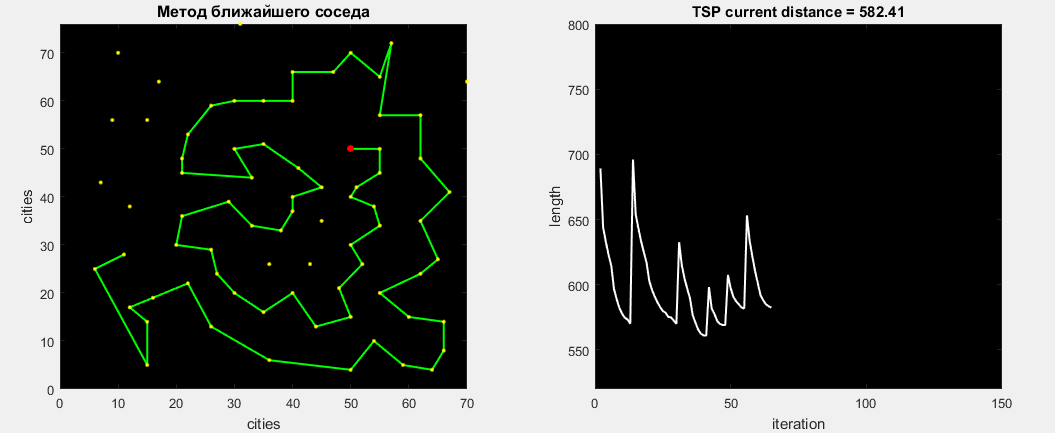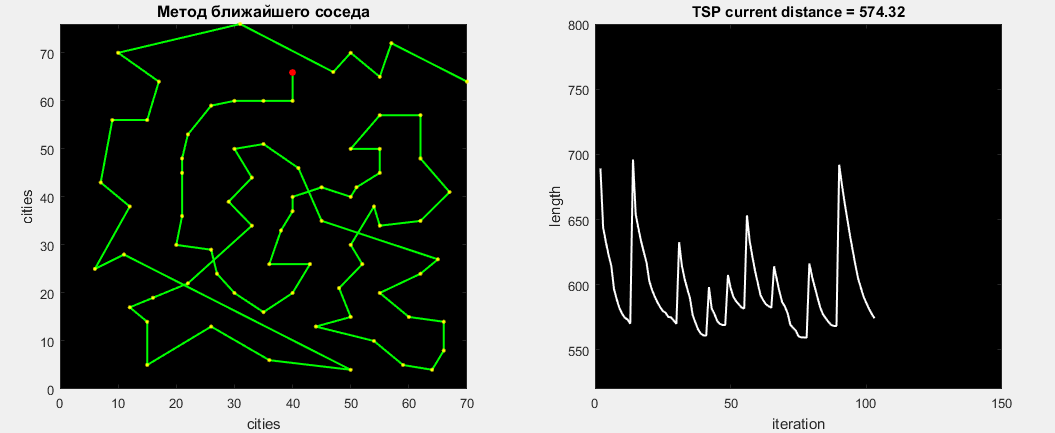
76の最適化すべてを完了した後、見つかった最適なルート-545を取得します。費やされた時間は0.15秒です。 このアルゴリズムは、ランダム性の部分がないため、常に545の距離を見つけます。 グローバルからのエラーは1.3%です。
今から楽しい部分です。 お気づきかもしれませんが、欲張りアルゴリズム、ブルートフォース法(網羅的検索)、およびシミュレーテッドアニーリングを混合しただけです。 ここで、少しアリのアルゴリズムを追加します。 このアルゴリズムでは、最適化機能に転送される前に、100%の確率で最も近い都市への移行が実行されます。 私たちのタスクは、見つかった最適なルートを見つけ、できるだけ多くの「数字」を作成し、関数に渡すことです。 antアルゴリズム(AS)で覚えているように、頂点iから頂点jへの遷移の確率は、次の式によって決定されます。
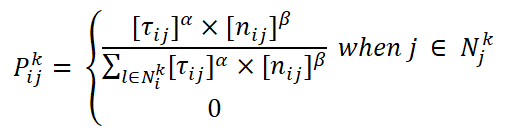
ここで、[τ(i、j)]はエッジ(i、j)のフェロモンのレベル、[n(i、j)]はエッジ(i、j)の距離の逆の重み、βは調整可能なパラメーター、アルゴリズムは、より短い距離のエッジを選択する傾向があります。 このアルゴリズムにはフェロモンがないため、削除します。 アルゴリズムの「欲」のレベルのみを残します。 ACSのように、未訪問のピークを選択する確率を実施します。 最短の都市のみを選択するか、次のように進みます。
次のrib骨を選択する確率は、その長さに反比例します。 また、まだ訪問していない都市の選択を担当する変数を紹介します。 つまり、次の頂点を選択するとき、残りのすべてを考慮するのではなく、N番目の残りの頂点から選択します。 Nは、ユーザーが指定したパラメーターです。 彼はこの考えを遺伝的アルゴリズムから取りました。 遺伝的アルゴリズムには、「選択」という概念があります。この段階では、現在の母集団全体から特定の割合を選択して「生存」する必要があります。 個人の生存確率は、フィットネス関数の値に依存する必要があります。 ここで、フィットネス関数の値はrib骨の距離であり、人口は訪問されていない残りの都市の割合です。 人口全体から、「個人」を1つだけ選択します。 1つのピーク。 次のrib骨を受け入れる確率の式は次の形式を取ります。
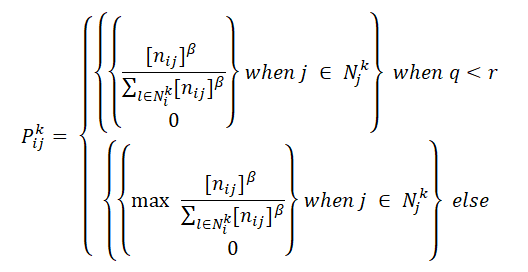
ここで、 qは代替決定を行う確率です(必ずしも最短エッジではありません)
r-乱数[0; 1]
N-選択に関与するエッジ(ソート可能)
したがって、all_brute関数の入力への「制御された」さまざまなルートを多数作成します。 制御されるという言葉は、ルートのランダム性の制御を意味します。 Nが都市の総数になる傾向があるように、パラメーターqが1になる傾向があるほど、検索はランダムになります。
ルーティング機能
% (probability several route) % , % dist - % tour_sev - - % n - - % tour_select - - % check_routes - % p_change - %------------------------------------------------------------------------- function [arr_several_route] = psr(dist,tour_sev,n,tour_select,cr,p_change) % () arr_several_route = zeros(tour_sev,n); parfor k = 1:tour_sev % ( ) dist_temp = dist; % route = zeros(1,n); % ( ) next_point = randi([1,n]); % route(1) = next_point; % count_var = 0; % for e = 2:n % dist_temp(next_point,:) = nan; % count_var = count_var + 1; % if rand(1) > p_change % k- % [~,next_point] = min(dist_temp(:,next_point)); else % % () arr_next = 1./(dist_temp(:,next_point)); % % , "habrahabr_vis" habrahabr_vis = (1:1:n)'; % arr_next = [arr_next, habrahabr_vis]; % arr_next_sort = sortrows(arr_next,1); % rand if (n - count_var) < tour_select tour_select_fun = (n - count_var); else tour_select_fun = tour_select; end % P = arr_next_sort(1:tour_select_fun,:); P(:,1) = P(:,1)./sum(P(:,1)); randNumb = rand; next_point = P(find(cumsum(P) >= randNumb, 1, 'first'),2); end % route(e) = next_point; end % 1- if cr == true route = check_tour(route); end % ( ) arr_several_route(k,:) = route; end
そのため、さまざまなタスクの結果を確認します。
正確なソリューション:
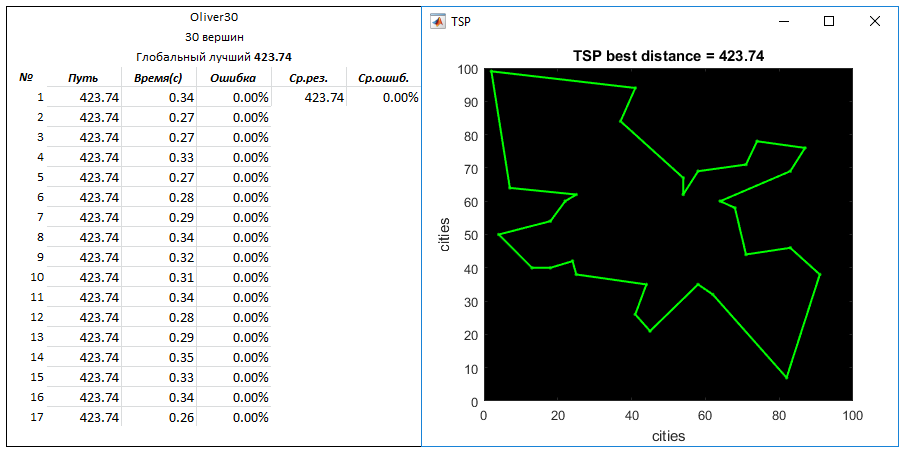
タスクOliver30 (30ピーク)。 グローバルベストウェイ-423.741
パラメータ: 作成されたエントリルートの数-500
q = 0.03
N = 10
タスクEil51 (51ピーク)。 グローバルベストウェイ-426
パラメータ: 作成されたエントリルートの数-2500
q = 0.03
N = 5
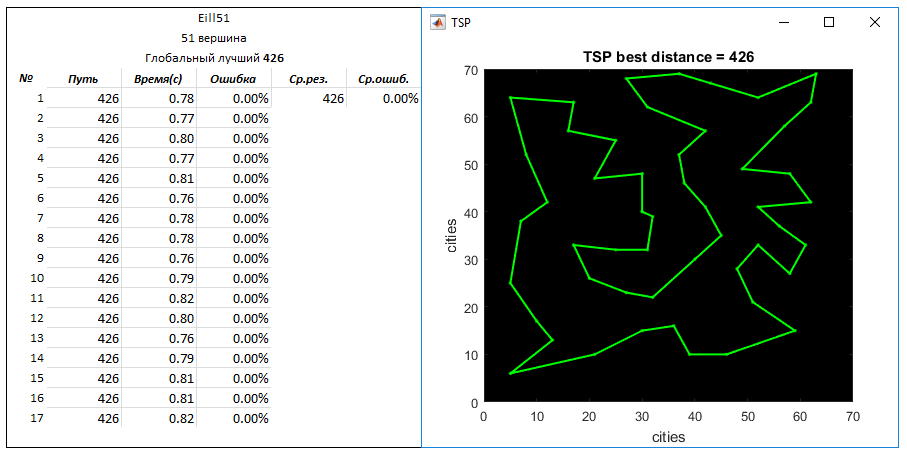
タスクEil76 (76ピーク)。 グローバルベストウェイ-538
パラメータ: 作成されたエントリルートの数-4000
q = 0.03
N = 10
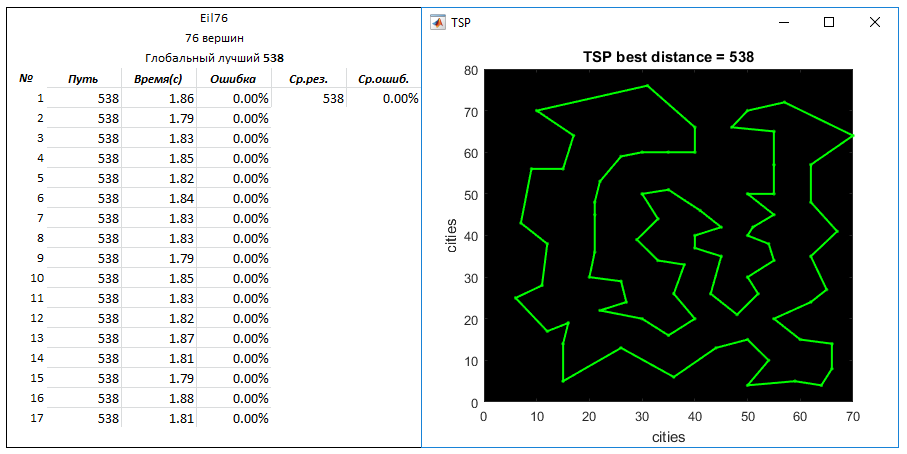
タスクEil101 (101ピーク)。 グローバルベストウェイ-629
パラメータ: 作成されたエントリルートの数-2500
q = 0.03
N = 6
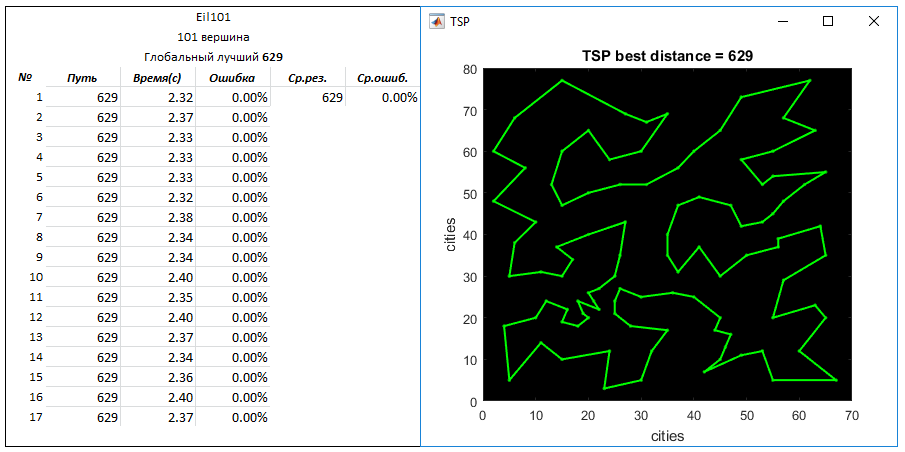
Ch150問題(150頂点)。 グローバルベストウェイ-6528
パラメータ: 作成されたエントリルートの数-40,000
q = 0.05
N = 10
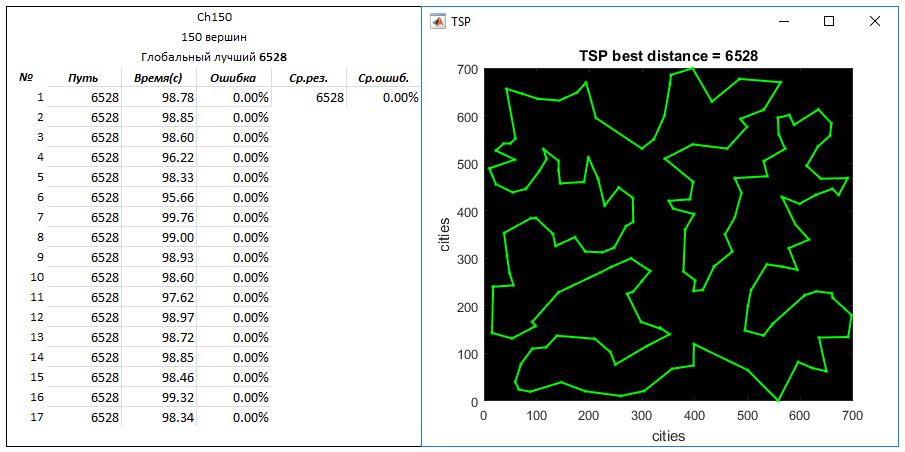
良い結果。 はい、このアルゴリズムは、アニーリングシミュレーション法や遺伝的アルゴリズムなどの発見的アルゴリズムよりもはるかに効率的です。 ただし、遺伝的アルゴリズムによる問題解決の範囲は非常に広く、このアルゴリズムについては言えません。 ただし、異なるアルゴリズムを混合した場合の結果を知ることは興味深いものでした。
このアルゴリズムの主な目的は、最適化されたルートの配列と距離の配列を作成することです。 次の記事では、この配列を使用して、遺伝的アルゴリズムとアリアルゴリズムを組み合わせます。 GPUで計算を使用します。 そして、非常に手頃な時間で、自宅のPCで500、1000、2000ピークのグローバルな最良の方法を見つけることを目指しましょう。 これから先、これは非常に現実的だと思います。
そのため、この記事では、今日のさまざまなタスクに見られる最良の方法を見つけました。 これまでに見つかった最良のソリューションとおおよそのソリューションとの間に大きなギャップがあります。 このアルゴリズムで近似解が見つかった場合、アルゴリズムの実行時間は10分の1になります。
以下はコメント付きのメインアルゴリズムコードです(その機能は上記で公開されています)
メイン
% TSP() ( ) %------------------------------------------------------------------------% if exist('cities','var') == 1 clearvars -except cities n = length(cities(:,1)); else clearvars intvar = inputdlg({'- '}... ,'TSP',1); n = str2double(intvar(1)); if isnan(n) || n < 0 msgbox ' ' return else cities = rand(n,2)*100; end end % tic %---------------------------------------------------------------% % ( x y ) start_tour = 1; % , % ( ) check_routes = false; % roulete_method = false; % (- ) if roulete_method == true crrm = 1000; end % "ts" top_roulete_method = true; if top_roulete_method == true % - " " ctrrm = 1000; % ts = 10; % p_change = 0.05; end %------------------------------------------------------------------% % dist = zeros(n,n); % () best_dist = inf; % brute_edge arr_route_in = zeros(n,n); % - ( ) % b = 1; %------------------------------------------------------------------------% % for i = 1:n for j = 1:n dist(i,j) = sqrt((cities(i,1) - cities(j,1))^2 + ... (cities(i,2) - cities(j,2))^2); end end % dist = round(dist); % returndist = 1./dist; % ( ) start_route = linspace(1,n,n); % if start_tour > n || start_tour < 1 start_tour = 1; end % "start_tour" start_route(start_tour) = 1; start_route(1) = start_tour; % % % parfor - parfor k = 1:n % ( ) dist_temp = dist; % route = zeros(1,n); % next_point = start_route(k); % route(1) = next_point; % for e = 2:n % dist_temp(next_point,:) = nan; % [~,next_point] = min(dist_temp(:,next_point)); % route(e) = next_point; end % 1- if check_routes == true route = check_tour(route); end % arr_route_in(k,:) = route; end % ( ) % if top_roulete_method == true arr_several = psr(dist,ctrrm,n,ts,check_routes,p_change); arr_route_in = [arr_route_in; arr_several]; end % % if roulete_method == true % , [randRoute] = prr(returndist,crrm,n,check_routes); % arr_route_in = [arr_route_in;randRoute]; end % % % parfor r = 1:size(arr_route_in, 1); % temp_route = arr_route_in(r,:); % [~,numb_ix] = find(temp_route == 1); % if numb_ix ~= 1 % temp_route = [temp_route(numb_ix:end),temp_route(1:numb_ix-1)]; % elseif numb_ix == n % temp_route = fliplr(temp_route); % end % arr_route_in(r,:) = temp_route; % end % , arr_route_in = unique(arr_route_in,'rows'); %------------------------------------------------------------------% % () arr_tour_out = zeros(size(arr_route_in,1),n); % () arr_result = zeros(size(arr_route_in,1),1); %------------------------------------------------------------------------% % ( ) spdvar = size(arr_route_in, 1); parfor i = 1:spdvar % [tour, distance] = all_brute_first(dist,arr_route_in(i,:),n); [tour, distance] = all_brute_best(dist,arr_route_in(i,:),n); arr_tour_out(i,:) = tour; arr_result(i,1) = distance; end % toc % [best_length,best_indx] = min(arr_result); % 1- best_route = arr_tour_out(best_indx,:); % % % mean(arr_result) %-----------------------------------------------------------------% tsp_plot = figure(1); set(tsp_plot,'name','TSP','numbertitle','off'... ,'color','w','menubar','none') set(gcf,'position',[2391 410 476 409]); opt_tour(:,[1,2]) = cities(best_route,[1,2]); plot([opt_tour(:,1);opt_tour(1,1)],[opt_tour(:,2);opt_tour(1,2)],'-g.', ... 'linewidth',1.5) set(gca,'color','k') title(['TSP best distance = ',num2str(round(best_length,2))]) xlabel('cities'); ylabel('cities') %------------------------------------------------------------------------% fprintf('%s %d\n',' ',round(best_length)); clearvars -except cities arr_result arr_tour_out arr_route_in ... n best_length opt_tour dist openclose
ご清聴ありがとうございました。 また会うまで。