Wellford法による平均と共分散の正確な計算

Wellfordメソッドは、平均、分散、共分散、およびその他の統計を計算するためのシンプルで効果的な方法です。 このメソッドには、多くの優れたプロパティがあります。

• 決定の精度に関して優れたパフォーマンスを達成します。
• 覚えて実装するのは非常に簡単です。
• これはワンパスオンラインアルゴリズムであり、状況によっては非常に便利です。

Wellfordのオリジナル記事は1962年に公開されました。 それにもかかわらず、アルゴリズムが現在何らかの形で広く知られているとは言えません。 そして、その正確さの数学的な証明や、他の方法との実験的比較を見つけることは完全に重要です。

この記事では、これらのギャップを埋めようとします。

内容

• はじめに
• 1.平均の計算におけるエラー
• 2.指定
• 3.平均の計算
• 4.共分散の計算
• 5.実験方法の比較
• おわりに

はじめに

開発者としての活動の最初の数か月で、機械学習法を作成しました。この方法では、葉に線形回帰モデルを含む決定木を勾配ブースティングの対象にしました。 そのようなアルゴリズムは、当時流行して勝利したコンセプトのピークに部分的に選ばれ、非常に単純なアルゴリズムの巨大な構成を構築しました。それどころか、かなり複雑なモデルの小さな構成を構築したかったのです。

このトピック自体は私にとって非常に興味深いものであることが判明したため、私はそれについて論文を書きさえしました。 数百本の木のモデルを構築するには、数万回の線形回帰問題を解く必要があり、これらのモデルのデータは非常に多様であり、多重共線性、正則化、および計算精度の問題は完全な高さであるため、すべてのケースで良質を達成することは困難であることが判明しました。 しかし、1つのツリーの1つのシートにある1つの不良モデルは、構成全体を完全に不適切にするのに十分です。

膨大な数の線形モデルの自動構築に関連する問題を解決する過程で、線形回帰タスク自体に関係しないものも含め、さまざまな状況で将来役に立つと思われる多くの事実を見つけることができました。 ここで、これらの事実のいくつかについてお話ししたいと思います。最初は、ウェルフォード法についてお話しすることにしました。

この記事の構造は次のとおりです。 パラグラフ1では 、平均を計算する最も単純なタスクを検討します。この例では、このタスクは一見すると思われるほど単純ではないことがわかります。 セクション2では、この記事で使用する表記法を紹介します。この表記法は、セクション3および4で役立ちます。それぞれ、加重平均および加重共分散の計算のためのウェルフォード法の公式の導出に当てられます。 数式の派生の技術的な詳細に興味がない場合は、これらのセクションをスキップできます。 セクション5には、メソッドの実験的比較の結果が含まれており、 結論としては、C ++でのアルゴリズムの実装例です。

共分散計算方法を比較するためのモデルコードは、私のgithubプロジェクトにあります。 Wellfordメソッドを使用して線形回帰の問題を解決するより複雑なコードは、次の記事で説明する別のプロジェクトにあります。

1.平均の計算におけるエラー

古典的な例から始めましょう。 一連の数値の平均を計算する単純なクラスがあるとします。

class TDummyMeanCalculator { private: float SumValues = 0.; size_t CountValues = 0; public: void Add(const float value) { ++CountValues; SumValues += value; } double Mean() const { return CountValues ? SumValues / CountValues : 0.; } };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次の方法で実践してみましょう。

 int main() { size_t n; while (std::cin >> n) { TDummyMeanCalculator meanCalculator; for (size_t i = 0; i < n; ++i) { meanCalculator.Add(1e-3); } std::cout << meanCalculator.Mean() << std::endl; } return 0; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

プログラムは何を出力しますか？

入る	おわりに
10,000	0.001000040
1,000,000	0.000991142
1億	0.000327680
200000000	0.000163840
300000000	0.000109227

ある時点から、次の用語の追加後に金額の変更が停止します。これは、 SumValues



が32768に等しい場合に発生しSumValues



float



型には、加算の結果を表すのに十分なビット深度がありません。

この状況から抜け出す方法はいくつかあります。

1. float
   
   
   
   からdouble
   
   
   
   移動します。
2. より複雑な加算方法のいずれかを使用します 。
3. Kahanメソッドを使用して要約します。
4. 最後に、 Wellfordメソッドを使用して 、平均を直接計算できます。

double



を使用したソリューションがうまく機能しないデータを見つけるのはそれほど簡単ではありません。 ただし、特により複雑なタスクでは、このようなデータが見つかります。 また、 double



を使用するとメモリコストが増加することも不快です。場合によっては、同時に多数の平均値を保存する必要があります。

Kahanの方法やその他の複雑な加算方法は独自の方法で優れていますが、将来的には、Wellfordの方法の方が優れた機能を発揮し、さらに驚くほど簡単に実装できることがわかります。 実際、対応するコードを見てみましょう。

 class TWelfordMeanCalculator { private: float MeanValues = 0.; size_t CountValues = 0; public: void Add(const float value) { ++CountValues; MeanValues += (value - MeanValues) / CountValues; } double Mean() const { return MeanValues; } };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

今後、このコードの正確性の問題に戻ります。 それまでの間、実装は非常に単純に見えますが、プログラムで使用されるデータでは、完全な精度でも機能します。 これは、差のvalue - MeanValues



最初の反復でのvalue - MeanValues



が平均に正確に等しく、後続の反復ではゼロに等しいという事実によるものです。

この例は、ウェルフォード法の主な利点を示しています。算術演算に関係するすべての量は大きさが「同等」であることが判明し、既知のように、計算の良好な精度に貢献します。

入る	おわりに
10,000	0.001
1,000,000	0.001
1億	0.001
200000000	0.001
300000000	0.001

この記事では、ウェルフォード法のさらに別の問題-共分散の計算の問題への適用を検討します。 さらに、さまざまなアルゴリズムを比較し、メソッドの正確性の数学的証明を取得します。

2.指定

正しい表記法を選択すると、多くの場合、式の結論は非常にシンプルで理解しやすくなります。 私たちも試してみます。 実数の2つのシーケンスが与えられると仮定します。 $$$x$ そして $$$y$ 、および対応する重みのシーケンス $$$w$ ：

$$

$$x = x_1、x_2、...、x_n、...$$

$$

$$y = y_1、y_2、...、y_n、...$$

$$

$$w = w_1、w_2、...、w_n、...$$

平均と共分散を計算したいので、加重和と積和の表記法が必要です。 同じ方法でそれらを説明してみましょう：

$$

$$S_n ^ {a、b、...、z} = \ sum_ {i = 1} ^ n {a_i \ cdot b_i \ cdot ... \ cdot z_i}$$

次に、例えば、 $$$S_n ^ {w}$ 最初の重みの合計です $$$n$ 要素 $$$S_n ^ {wx}$ 最初の加重和です $$$n$ 最初のシーケンスの番号、および $$$S_n ^ {wxy}$ -加重製品の合計：

$$

$$S_n ^ {w} = \ sum_ {i = 1} ^ n {w_i}$$

$$

$$S_n ^ {wx} = \ sum_ {i = 1} ^ n {w_i \ cdot x_i}$$

$$

$$S_n ^ {wxy} = \ sum_ {i = 1} ^ n {w_i \ cdot x_i \ cdot y_i}$$

加重平均値も必要です。

$$

$$m_n ^ {wx} = \ frac {\ sum_ {i = 1} ^ n {w_i \ cdot x_i}} {\ sum_ {i = 1} ^ n {w_i}} = \ frac {S_n ^ {wx}} {S_n ^ w}$$

$$

$$m_n ^ {wy} = \ frac {\ sum_ {i = 1} ^ n {w_i \ cdot y_i}} {\ sum_ {i = 1} ^ n {w_i}} = \ frac {S_n ^ {wy}} {S_n ^ w}$$

最後に、正規化されていない「散布」の表記法を紹介します $$$D_ {n} ^ {wxy}$ および正規化された共分散 $$$C_ {n} ^ {wxy}$ ：

$$

$$D_ {n} ^ {wxy} = \ sum_ {i = 1} ^ {n} w_i（x_i-m_ {n} ^ {wx}）（y_i-m_ {n} ^ {wy}）$$

$$

$$C_ {n} ^ {wxy} = \ frac {D_ {n} ^ {wxy}} {S_ {n} ^ w} = \ frac {\ sum_ {i = 1} ^ {n} w_i（x_i-m_ {n} ^ {wx}）（y_i-m_ {n} ^ {wy}）} {\ sum_ {i = 1} ^ {n} w_ {i}}$$

3.平均の計算

ウェルフォード法で平均を計算するために上記で使用した式の重み付き類似体を証明しましょう。 違いを考慮してください $$$m_ {n + 1} ^ {wx}-m_ {n} ^ {wx}$ ：

$$

$$m_ {n + 1} ^ {wx}-m_ {n} ^ {wx} = \ frac {S_ {n + 1} ^ {wx}} {S_ {n + 1} ^ {w}}-\ frac {S_ {n} ^ {wx}} {S_ {n} ^ {w}} = \ frac {S_ {n} ^ {w} S_ {n + 1} ^ {wx}-S_ {n} ^ {wx } S_ {n + 1} ^ {w}} {S_ {n + 1} ^ {w} S_ {n} ^ {w}} =$$

$$

$$= \ frac {S_ {n} ^ {w} S_ {n} ^ {wx} + w_ {n + 1} x_ {n + 1} S_n ^ w-S_ {n} ^ {wx} S_ {n} ^ {w}-w_ {n + 1} S_n ^ {wx}} {S_ {n + 1} ^ {w} S_ {n} ^ {w}} = \ frac {w_ {n + 1} x_ {n +1} S_n ^ w-w_ {n + 1} S_n ^ {wx}} {S_ {n + 1} ^ {w} S_ {n} ^ {w}}$$

$$

$$= \ frac {w_ {n + 1}} {S_ {n + 1} ^ {w}} \ Big（x_ {n + 1}-\ frac {S_n ^ {wx}} {S_n ^ w} \ Big ）= \ frac {w_ {n + 1}} {S_ {n + 1} ^ {w}}（x_ {n + 1}-m_n ^ {wx}）$$

特に、すべての重みが1に等しい場合、次を取得します。

$$

$$m_ {n + 1} ^ {wx} = m_ {n} ^ {wx} + \ frac {x_ {n + 1}-m_n ^ {wx}} {n + 1}$$

ちなみに、「重み付き」ケースの式を使用すると、連続した数字を1つだけ追加する以外の操作を簡単に実装できます。 たとえば、番号を削除する $$$x$ 平均の計算に使用されるセットからの計算は、数値の追加と同じです $$$-x$ 重量で $$$-1$ 。 複数の数字を一度に追加することは、これらの数字の数に等しい重みを持つ中央の1つを追加することと同じです。

4.共分散の計算

共分散を計算するための古典的な式は、加重問題にも当てはまることを示します。 簡単にするために、正規化されていない値を使用します。

$$

$$D_ {n} ^ {wxy} = \ sum_ {i = 1} ^ {n} w_i（x_i-m_n ^ {wx}）（y_i-m_n ^ {wy}）= S_n ^ {wxy}-m_n ^ { wx} S_n ^ {wy}-S_n ^ {wx} m_n ^ {wy} + S_n ^ wm_n ^ {wx} m_n ^ {wy}$$

ここから、それはすでに簡単にわかります

$$

$$D_ {n} ^ {wxy} = S_n ^ {wxy}-\ frac {S_n ^ {wx} S_n ^ {wy}} {S_n ^ w}$$

ただし、オンラインアルゴリズムを含め、この式は非常に便利です。 $$$S_n ^ {wxy}$ そして $$${S_n ^ {wx} S_n ^ {wy}} / {S_n ^ w}$ 近い値であり、同時に絶対値が大きい場合、その使用は重大な計算エラーにつながります。

の繰り返し式を導出してみましょう $$$D_n ^ {wxy}$ 、ある意味では、平均のウェルフォード式に似ています。 だから：

$$

$$D_ {n + 1} ^ {wxy} = S_n ^ {wxy} + w_ {n + 1} x_ {n + 1} y_ {n + 1}-w_ {n + 1} x_ {n + 1} \ frac {S_ {n + 1} ^ {wy}} {S_ {n + 1} ^ {w}}-\ frac {S_n ^ {wx} S_ {n + 1} ^ {wy}} {S_ {n + 1} ^ w} =$$

$$

$$= S_n ^ {wxy} + w_ {n + 1} x_ {n + 1}（y_ {n + 1}-m_ {n + 1} ^ {wy}）-\ frac {S_n ^ {wx} S_ { n + 1} ^ {wy}} {S_ {n + 1} ^ w}$$

最後の用語を考慮してください：

$$

$$\ frac {S_n ^ {wx} S_ {n + 1} ^ {wy}} {S_ {n + 1} ^ w} = \ Big（\ frac {1} {S_n ^ w}-\ frac {w_ { n + 1}} {S_n ^ wS_ {n + 1} ^ w} \ Big）S_n ^ {wx} S_ {n + 1} ^ {wy} = \ frac {S_n ^ {wx} S_ {n + 1} ^ {wy}} {S_n ^ w} -w_ {n + 1} m_n ^ {wx} m_ {n + 1} ^ {wy} =$$

$$

$$= \ frac {S_n ^ {wx} S_ {n} ^ {wy}} {S_n ^ w} + w_ {n + 1} y_ {n + 1} \ frac {S_n ^ {wx}} {S_n ^ w } -w_ {n + 1} m_n ^ {wx} m_ {n + 1} ^ {wy} = \ frac {S_n ^ {wx} S_ {n} ^ {wy}} {S_n ^ w} + w_ {n +1} m_n ^ {wx} \ cdot（y_ {n + 1} -m_ {n + 1} ^ {wy}）$$

結果の式を $$$D_ {n + 1} ^ {wxy}$ ：

$$

$$D_ {n + 1} ^ {wxy} = S_n ^ {wxy} + w_ {n + 1} x_ {n + 1}（y_ {n + 1}-m_ {n + 1} ^ {wy}）- \ frac {S_n ^ {wx} S_ {n} ^ {wy}} {S_n ^ w} -w_ {n + 1} m_n ^ {wx} \ cdot（y_ {n + 1} -m_ {n + 1} ^ {wy}）=$$

$$

$$= \ Big [S_n ^ {wxy}-\ frac {S_n ^ {wx} S_ {n} ^ {wy}} {S_n ^ w} \ Big] + w_ {n + 1}（x_ {n + 1} -m_n ^ {wx}）（y_ {n + 1}-m_ {n + 1} ^ {wy}）=$$

$$

$$= D_ {n} ^ {wxy} + w_ {n + 1}（x_ {n + 1} -m_n ^ {wx}）（y_ {n + 1}-m_ {n + 1} ^ {wy}）$$

この式を使用した計算を実装するコードは、重みがない場合、非常に単純に見えます。 2つの平均値と作業量を更新する必要があります。

 double WelfordCovariation(const std::vector<double>& x, const std::vector<double>& y) { double sumProducts = 0.; double xMean = 0.; double yMean = 0.; for (size_t i = 0; i < x.size(); ++i) { xMean += (x[i] - xMean) / (i + 1); sumProducts += (x[i] - xMean) * (y[i] - yMean); yMean += (y[i] - yMean) / (i + 1); } return sumProducts / x.size(); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

また興味深いのは、共分散自体の値を更新するという質問です。 正規化された値：

$$

$$C_ {n + 1} ^ {wxy} = \ frac {\ sum_ {i = 1} ^ {n + 1} w_i（x_i-m_ {n + 1} ^ {wx}）（y_i-m_ {n + 1} ^ {wy}）} {\ sum_ {i = 1} ^ {n + 1} w_ {i}} = \ frac {D_ {n + 1} ^ {wxy}} {S_ {n + 1} ^ w} =$$

$$

$$= \ frac {1} {S_ {n + 1} ^ w} \ cdot \ Big（D_n ^ {wxy} + w_ {n + 1}（x_ {n + 1} -m_n ^ {wx}）（y_ {n + 1}-m_ {n + 1} ^ {wy}）\ Big）=$$

$$

$$= \ frac {D_n ^ {wxy}} {S_ {n + 1} ^ w} + \ frac {w_ {n + 1}} {S_ {n + 1} ^ w}（x_ {n + 1}- m_n ^ {wx}）（y_ {n + 1}-m_ {n + 1} ^ {wy}）$$

最初の用語を考えます：

$$

$$\ frac {D_n ^ {wxy}} {S_ {n + 1} ^ w} = \ Big（\ frac {1} {S_n ^ w}-\ frac {w_ {n + 1}} {S_ {n + 1} ^ wS_n ^ w} \ Big）D_n ^ {wxy} = \ frac {D_n ^ {wxy}} {S_n ^ w} \ Big（1-\ frac {w_ {n + 1}} {S_ {n + 1} ^ w} \ Big）= C_n ^ {wxy} \ Big（1- \ frac {w_ {n + 1}} {S_ {n + 1} ^ w} \ Big）$$

検討に戻りましょう $$$C_ {n + 1} ^ {wxy}$ ：

$$

$$C_ {n + 1} ^ {wxy} = C_n ^ {wxy} \ Big（1- \ frac {w_ {n + 1}} {S_ {n + 1} ^ w} \ Big）+ \ frac {w_ {n + 1}} {S_ {n + 1} ^ w}（x_ {n + 1} -m_n ^ {wx}）（y_ {n + 1}-m_ {n + 1} ^ {wy}）$$

これは、たとえば次のように書き換えることができます。

$$

$$C_ {n + 1} ^ {wxy} = C_n ^ {wxy} + \ frac {w_ {n + 1}} {S_ {n + 1} ^ w} \ Big（（x_ {n + 1} -m_n ^ {wx}）（y_ {n + 1}-m_ {n + 1} ^ {wy}）-C_n ^ {wxy} \ Big）$$

結果は、平均を更新するための式に本当に驚くほど似ている式です！

5.実験方法の比較

共分散を計算するための3つの方法を実装する小さなプログラムを作成しました。

1. 数量を直接計算する「標準」アルゴリズム $$$S_n ^ {wxy}$ 、 $$$S_n ^ {wx}$ そして $$$S_n ^ {wy}$ 。
2. Kahanメソッドを使用したアルゴリズム。
3. Wellfordメソッドを使用したアルゴリズム。

タスクのデータは次のように形成されます。2つの数字が選択され、 $$$m_x$ そして $$$m_y$ -2つのサンプルの平均。 次に、さらに2つの番号が選択されます。 $$$d_x$ そして $$$d_y$ -したがって、偏差。 アルゴリズムへの入力は数字のシーケンスです

$$

$$x_i = m_x \ pm d_x、$$

$$

$$y_i = m_y \ pm d_y、$$

さらに、偏差のある符号は反復ごとに変化するため、真の共分散は次のように計算されます。

$$

$$C_ {n} ^ {xy} = \ frac {\ sum_ {i = 1} ^ {n}（x_i-m_x）（y_i-m_y）} {n} = d_x \ cdot d_y$$

真の共分散は定数であり、項の数に依存しないため、各反復で各メソッドの相対計算誤差を計算できます。 したがって、現在の実装では $$$d_x = d_y = 1$ 、および平均は100,000および1,000,000の値を取ります。

最初のグラフは、平均10万の単純メソッドを使用した場合の相対誤差の依存性を示しています。 このグラフは、単純な方法の失敗を示しています。ある時点から、エラーが急速に増大し始め、完全に許容できない値に達します。 同じデータで、KahanとWelfordのメソッドは重大なエラーを許可しません。

2番目のグラフは、平均が100万のKahanメソッド用に作成されています。 項の数が増えてもエラーは増加しませんが、「ナイーブ」メソッドのエラーよりも大幅に低くなりますが、実際のアプリケーションにはまだ大きすぎます。

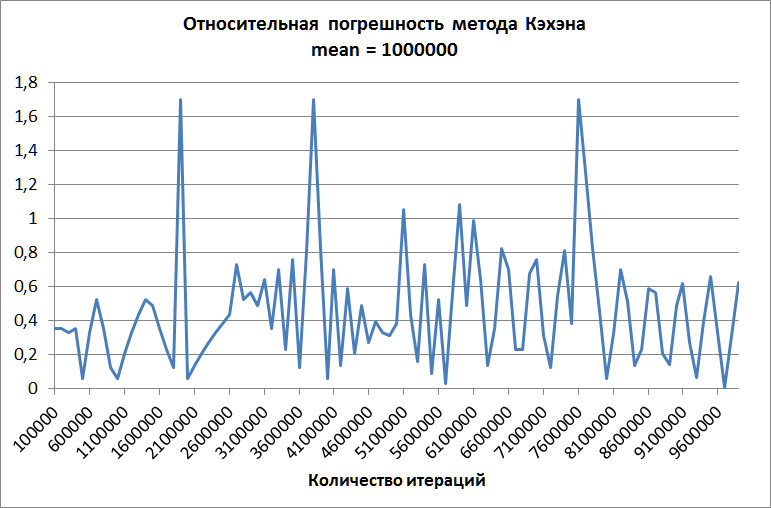
ウェルフォードの方法は、順番に、そしてこのデータで完璧な精度を実証しています！

おわりに

この記事では、共分散を計算するためのいくつかの方法を比較し、Wellfordメソッドが最良の結果をもたらすことを確認しました。 実際に使用するには、次の2つの実装のみを覚えておけば十分です。

 class TWelfordMeanCalculator { private: double Mean = 0.; size_t Count = 0; public: void Add(const float value) { ++Count; Mean += (value - Mean) / Count; } double GetMean() const { return Mean; } }; class TWelfordCovariationCalculator { private: size_t Count = 0; double MeanX = 0.; double MeanY = 0.; double SumProducts = 0.; public: void Add(const double x, const double y) { ++Count; MeanX += (x - MeanX) / Count; SumProducts += (x - MeanX) * (y - MeanY); MeanY += (y - MeanY) / Count; } double Covariation() const { return SumProducts / Count; } };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これらの方法を使用すると、データがかなり「不適切」に配置されている状況で多くの時間と労力を節約できます。 1次元のkMeansアルゴリズムを実装している場合でも、予想外の状況では、計算の精度に問題が発生する場合があります。

次の記事では、線形回帰回復問題で考慮された方法の適用を検討し、計算の速度と、機械学習方法の一般的な実装が「不良」データに対処する方法について説明します。

文学

1. github.com： さまざまな共変動計算方法
2. machinelearning.ru： サイズが大幅に異なる大きな数字のセットの追加
3. en.wikipedia.org： カハンアルゴリズム
4. en.wikipedia.org： 分散を計算するためのアルゴリズム：オンラインアルゴリズム