🤘🏼 ⛹🏿 🕊️ 量子後暗号と日没RSA-本当の脅威か想像上の未来か？ 👩🏻‍🔧 💦 🕺

RSA、楕円曲線、量子コンピューター、同質性...一見すると、これらの単語はある種の呪文に似ていますが、すべてが思ったよりもはるかに複雑です！

量子コンピューターへの攻撃に耐性のある暗号化への移行の必要性は、 NISTとNSAによって既に公式に発表されており、結論は非常に簡単です。快適なゾーンから脱出する時です！

したがって、古き良きRSAから、そしておそらく、多くの人が愛し、秘密情報を保護することができる、それほど面白くないプリミティブを学ぶ楕円曲線から離れる価値があります。

楕円曲線上の暗号化の複雑さを理解し、ポスト量子暗号化の最新の傾向を追跡し、Microsoft SIDHライブラリを使用してそれに触れることも、catへようこそ、 ％username％ ！

1.基本から始めましょう：暗号について少し説明します

暗号とは何ですか？たとえば、アリスとボブはメッセージを交換したいので、その内容は秘密にされています。明らかに、各側には独自のキーが必要です。そしてこの段階で、暗号システムの2つの亜種を区別できます。

それらの最初のものには、対称暗号システムが含まれます。ここで、あるキーは別のキーから簡単に計算でき、多くの場合完全に一致します。このような暗号システムの重要な利点は、実装が容易であり、より単純な操作を使用するため、操作が高速であることです。ただし、キーの1つが危険にさらされると、機密情報を保護しようとしても意味が失われます。

この問題は、特殊なアルゴリズムを使用した非対称暗号システムでエレガントに解決されます。ただし、ここでは、大量のデータに対しては効率が悪い操作の複雑さに直面しています。このような暗号システムでは、1つのキーから他のキーを計算するために非常に一生懸命努力する必要があり、誰かのコンピューターには~~ダークサイドの~~大きな力はありませんが、保護されたデータの機密性は比較的穏やかです。

興味深い多方面...さて、それはどのように実装されていますか？それはすべて、いわゆる一方向関数についてです。機能がある $y = f（x）$ 。有名な議論による $x$ 関数値を計算する $y$ 3つのドラゴンと完璧な軍隊でWesterosを占領するよりも簡単です。ただし、引数の計算 $x$ 関数の既知の値によって $y$ かなり時間がかかるタスクです。

片側関数の最も有名な候補は、数を素因数に分解することから成る数因数分解問題と、未知のものを見つけることから成る離散対数問題です。 $k$ 既知の値による $y$ そして $g$ 満たすもの： $y = g ^ k$ 。たとえば、最初のものはよく知られているRSA暗号システムで使用され、2番目はDiffie-Hellman鍵確立スキームで使用できます。

しかし、ドラゴンの飛行のようなコンピューティングデバイスのパフォーマンスの急速な成長を考えると、キーの長さを増やす必要がありますが、これは電力が限られたデバイスにとって重要な要素になる可能性があります。同じレベルの耐久性を持つキー ...そして、幸いなことに、それは存在します！この奇跡の名前は楕円曲線です。

2.さらに複雑になりました：楕円曲線

顔がハロルドのような表現を採用している場合は、急いで記事を閉じて、神経質な笑いで逃げないでください。楕円曲線-簡単です！まず、定義を与えましょう。楕円曲線は、まず第一に、 ~~女性の~~非特異な3次曲線です。すべてのポイントに明確に接線を引くことができるため、彼らはそれを非特異と呼びます。さて、これは3次曲線であるため、3次方程式で与えられるべきです。これは、ワイエルシュトラスの一般化された形式では次のようになります。

y^{2} + a_{1} x y + a_{3} y = x^{3} + a_{2} x^{2} + a_{4} x + a_{6}

$y ^ 2 + a_1 xy + a_3y = x ^ 3 + a_2x ^ 2 + a_4x + a_6$

ただし、実際には、このような曲線の形状はまれにしか見つかりません。ルジャンドル、モンゴメリー、ヘッセなどの形式があります。いずれかの形式を使用すると、楕円曲線の点に対する操作の効率が向上します。たとえば、Montgomery形式では、 Montgomeryラダーアルゴリズムのおかげで、一定時間内にポイントを数値で乗算することが可能です。

確かに多くの人がワイエルシュトラスの形に出くわしました。 $char K \ neq 2.3$ ：

E （ K ） ： y^{2} = x^{3} + a x + b

$E（K）：y ^ 2 = x ^ 3 + ax + b$

楕円曲線の重要な特性はその判別式です 。これは、ワイエルシュトラス形式では次のように計算されます。

\デ ル タ = 4 a^{3} + 27 b^{2}

$\デルタ= 4a ^ 3 + 27b ^ 2$ 。

判別式はゼロに等しくてはなりません 。そうしないと、曲線のように変曲点があるため、曲線は楕円になりません。 $y ^ 2 = x ^ 3-3x + 2$ 右の図。

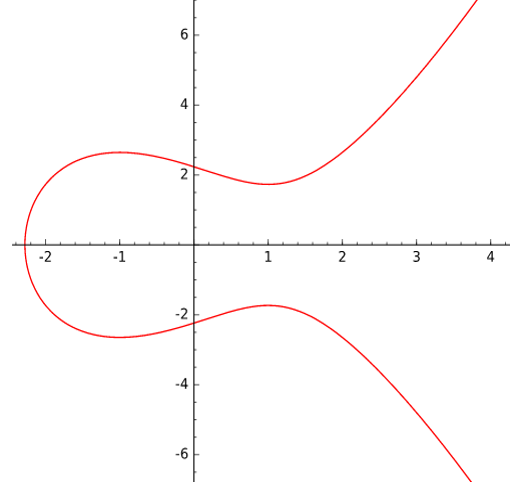
確かに多くの人が左の図に見られる楕円曲線の画像に精通しています。ここにフォームの曲線があります

y^{2} = x^{3} - 3 x + 5

$y ^ 2 = x ^ 3-3x + 5$ 有理数の体に与えられます。

画像の代替

ただし、有理数を使用する場合、丸めには困難があり、その結果、暗号化および復号化操作のあいまいさがあります。 そのため、暗号では、楕円曲線は有限フィールド上で定義されます 。ここで、ポイントの座標はフィールドの要素です。もちろん、曲線グラフは以前の魅力を失い、滑らかな線は点に置き換えられますが、私たちはそれから遠く離れた楕円曲線が大好きです！

楕円曲線のもう1つの特徴に言及するのを忘れることはできません。これは（スポイラー！）読者にこの記事での存在感を与え続けます。についてです $j-$ 不変、定数。ワイエルシュトラスの形の楕円曲線の計算も、体に恐ろしい効果はありません。 $j = 1728 \ frac {4a ^ 3} {4a ^ 3 + 27b ^ 2}$

グループのプロパティ

楕円曲線上の暗号法の重要な点は、抽象的な無限遠点を持つ楕円曲線の点がアーベル群を形成することです。 グループ演算として加算を行うと、グループは次のプロパティを持つ代数構造になります。

クロージャとは、グループの要素を追加した結果がグループの要素でもあることを意味します。楕円曲線の用語に変換しましょう。楕円曲線の点を追加すると、同じ曲線に属する点が得られます。

上の図からわかるように、楕円曲線に点を追加する幾何学的な意味は次のとおりです：折り畳み点に割線を描き、Ox軸に対する楕円曲線とこの線の交点を反映する必要があります。
結合性とは、加算の結果がアクションの順序を変えることから独立していることを意味します。
グループには中立要素が存在する必要があります。グループの要素を追加した結果 $g$ 楕円曲線では、中立要素の役割は無限遠点によって果たされます。 $P_ \ infty：P_ \ infty + P = P + P_ \ infty = P$
各要素には、それとは逆の関係が必要です（メイン操作に関連）。グループとその逆の要素を追加すると、中立的な要素が得られます。
可換性の性質は、学校の数学でもよく知られています。合計は用語の再配置によって変わりません。グループをアーベルにするのはこのプロパティです。

永続性についてのいくつかの言葉

次に、離散対数問題に基づいた暗号システムの強度について少し話しましょう。させる $G$ -有限巡回群、つまり、その各要素は、単一の要素の次数として表すことができます-行列 $g$ ： $<g \> = G = \ {1、g ^ 2、g ^ 3、...、g ^ {q-1} \}$ 。

グループの選択に応じて $G$ 離散対数問題を解くにはさまざまな方法があります。したがって、一般的な幸福のために、有限体の離散対数問題を解くには、 普遍的なアルゴリズム（Polyg-Hellman法、 $\ rho$ -Pollardの方法など）。指数関数的複雑さを持ちますが、準指数関数的複雑さを持つ特別なものもあります（分解ベース法、数値フィールドふるい法）。

フォーミンググループとして $G$ 楕円曲線のポイントを取ると、暗号ログは普遍的なアルゴリズムのみで満足する必要があります。したがって、楕円曲線の暗号化は、より短いキー長でユーザーを「甘やかします」。

ただし、すべての楕円曲線が暗号プロトコルで高レベルの強度を提供できるわけではありません。最初の危険は超特異曲線です。それらの利点は、非超特異曲線とは対照的に、ポイント数の計算が簡単なことです。超特異曲線と非超特異曲線を区別できる要因は多数ありますが、この記事ではこの点に焦点を当てません。

これらの曲線はMOV攻撃に対して脆弱です 。これにより、フィールド上の楕円曲線の点群における離散対数問題の計算を減らすことができます。 $\ mathbb {F} _q$ 有限体の離散対数問題 $\ mathbb {F_q ^ k}$ 。楕円曲線の暗号のキーの長さが短く、超特異曲線のキーの長さが与えられると、値 $k$ 攻撃者にとって、この攻撃の実装は非常に成功しています。

それで問題は何ですか？適切な楕円曲線を使用して生活を楽しんでいます！しかし、そこには...

3.量子の脅威

最近、量子コンピューティングの人気が高まっています。古典的なコンピューターでは、情報の最小単位がビットで表され、一度に0または1の値をとることができる場合、量子1では、この役割はqubitsによって果たされます。彼らの特徴は、 量子ビットが状態0と状態1の両方に同時にあることができるということです。これにより、量子コンピューターに優れた計算能力が与えられます。たとえば、4ビットの情報を考慮した場合、16種類の状態のすべての種類から、一度に1つしか選択できません。 4量子ビットは、同時に16状態、つまり重ね合わせ状態になり、この依存性は新しい量子ビットごとに指数関数的に増加します。

古典的なコンピューターの論理要素が入力で情報のビットを受け取り、明確に決定された結果が出力される場合、量子コンピューターでは、いわゆる量子ゲート（量子ゲート）が論理要素として扱われ、重ね合わせ全体の値を操作します。

量子ビットに特徴的な重要な現象は混乱です。たとえば、2つのもつれたキュービットがあります。それらの1つの状態を測定すると、検証を行うことなく、ペアの状態に関する情報を見つけるのに役立ちます。

量子コンピューターは、すべての種類の重ね合わせを使用する必要がある計算操作を実行する場合にのみ高速であるため、私たちにとって馴染みのある古典的なコンピューターの代わりではないことに注意してください。そのため、このようなマシンを使用して猫と一緒にビデオを見るのは完全に非現実的です。

一方で、量子コンピューターの出現はクールです。真剣に。科学の多くの分野では、このようなマシンは多くの利点をもたらします（たとえば、モデリングにおいて）が、暗号化にとっては、このような重要なブレークスルーが重要になります。そして、すべて1994年に、ピーターショアは、数億年ではなく、かなり目に見える時間で数を増やすことができる量子アルゴリズムを提案しました。

Shoreアルゴリズムについて

このアルゴリズムの修正により、離散対数問題を解くことができます。一般に、Shore法は、古典的なコンピューターでは特定の関数の順序を計算するのが難しい問題を減らすことにあります。 数値の因数分解または因数分解問題を考慮する場合、関数自体が使用されます $f（x）= a ^ x（mod \、N）$ どこで $N-$ 展開されている番号、および $a-$ 特別に選択された値、相互にシンプル $N$ 。アルゴリズムに沿ってさらに機能期間があります $w$ 次の関係を満たします。 $f（x + w）= f（x）$ そして、その結果、 $a ^ w = 1（mod \、N）$ 。見つかった期間から、数値の固有値を計算します $N$ ユークリッドアルゴリズムの使用： $gcd（a ^ \ frac {w} {2}、N）$ 。

離散対数問題を解くため、つまり、 $k$ によると $y = g ^ k$ 、つまり、別の関数の次数を計算する必要があります。 $f（x_1、x_2）= g ^ {x_1} y ^ {x_2}$ どこで $g-$ 等しい要素数でグループを形成する $q$ 。関数の期間は数字のペアで表されます $（w_1、w_2）$ ： $f（w_1 + x_1、w_2 + x_2）= f（x_1、x_2）$ 。離散対数問題の解は次の形式になります。 $k =-\ frac {w_1} {w_2}（mod \、q）$ 。

したがって、ショア法では、 量子部分と古典部分を区別することができ、アルゴリズムの量子部分のタスクは、重ね合わせ法を使用して関数の周期を見つけることです。

そのようなアルゴリズムの存在と量子コンピューターを開発する傾向が特別な組織を考えさせたのは驚くことではありません。たとえば、米国国家安全保障局は2015年に、量子コンピューター攻撃に耐性のあるアルゴリズムへの移行計画を発表しました。そして2016年に、NIST USAはポスト量子暗号アルゴリズムの開発のための提案の募集の開始を正式に発表しました。

事後量子暗号法は1つのプリミティブに限定されず、実際、いくつかの候補が現在検討されています。これらには、たとえば、ラティス上の高速暗号化プロトコル、ハッシュ関数スキーム（たとえば、 Merkleの署名）、および非可換代数に基づく暗号システム（たとえば、三つ編みグループ）が含まれます。私たちは、楕円曲線に密接に関連している（私たちはそれらをとても愛しています！）、つまり同質性を選択しました 。

4.同質性は私たちを救います！

概念から始めましょう。同質性は、単一の楕円曲線の点を同質遺伝子曲線の点に取り、無限にある点を無限に静止したままにする有理写像です 。 2つの同質な楕円曲線があるとします $E_1$ そして $E_2$ 。 1つのフィールドで定義され、同じ数のポイントを持つ場合、それらは同質遺伝子と呼ばれます。

そのため、 同質性は実際には小さなVZHUHであり、曲線点を取ります $E_1$ 入力で、出力で曲線に点を与える $E_2$ 。同質性の核は 、曲線上の点の集合です $E_1$ 曲線の無限遠点に行く $E_2$ 。

各同質性に対して、逆変換を実行する単一の二重同質性があります。つまり、同質性が次の形式を持っている場合： $\ phi：E_1 \右矢印E_2$ その後、彼女にデュアル： $\ hat {\ phi}：E_2 \右矢印E_1$ 。

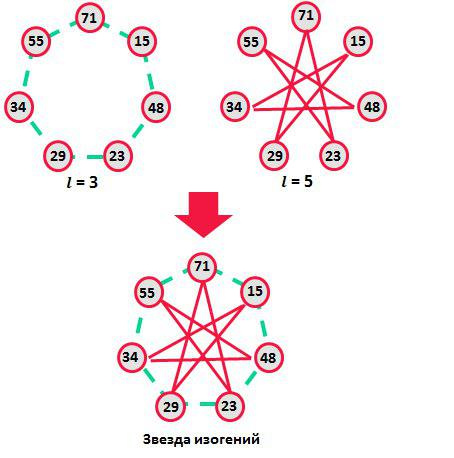
同質性とそれに双対を掛けると、曲線の点が得られます $E_2$ 整数倍 $l$ 、これは同質性の程度と呼ばれます。単純な次数の同型は集合の順列を定義できます $j-$ 同質曲線の不変量 。以下の図のように、同質な楕円曲線のグラフが連続して重なり合うことにより、宇宙的に美しい同質遺伝子曲線の星を取得することができます。

暗号システムを構築するために同質性を使用する可能性が比較的最近提案されました。 2003年に、著者のE. Teskeは、キーを預ける可能性のあるスキームで同質性が使用された作品を発表しました。 2006年、A.G。RostovtsevとA. Stolbunovでは、El Gamal暗号化スキームが楕円曲線の同質性に適合しました。また、2006年には、ハッシュ関数を構築するために、同質の超特異曲線のグラフを使用することが提案されました。重要な、そして言うかもしれないが、同質性の研究における転機は、2010年に発表された研究であり、準指数時間で非超特異曲線の同質性を見つける問題を解決する量子アルゴリズムを提案します。この時点から、研究は超特異曲線に焦点を合わせています。そのため、ネットワーク上では、公開鍵暗号化スキーム、ゼロ開示の証拠、否定できない署名およびブラインド署名のスキームをすでに見つけることができます。

5. Microsoft SIDH：どんな種類のポケモン？

マイクロソフトもまた、2016年にオープンソースSIDHライブラリ（Supersingular Isogeny Key Exchange）をリリースしました。このライブラリの利点の1つは、時間攻撃から保護する、モンゴメリーの形をした楕円曲線を使用できることです。

SIDHはCで実装され 、OC WindowsではMicrosoft Visual Studio、OC LinuxではLNU GCCおよびclangの使用をサポートしています。このライブラリは、x64、x86、ARMなどのさまざまなプラットフォームをサポートする機能を備えた基本的な算術関数の実装を提供します。パフォーマンスの大きな利点は、楕円曲線の操作の最適化された実装です。

このライブラリは、超特異曲線の同質性に関するDiffie-Hellmanキー分離プロトコルを実装しています。

このスキームは、JaoとDeFeoによって提案されました。簡略化すると、次のように説明できます。暗号システムのパラメーターとして、よく知られている超特異曲線が使用されます $E_0$ そしてその上の固定小数点 $P_A、Q_A、P_B、Q_B$ 。便宜上、プロトコルは次の図で監視できます。

アリスに、人生ではなく秘密鍵をボブと共有させたい。これを行うには、乱数を生成します $m_A、n_A$ 同質性を構築します $\ phi_A：E_0 \右矢印E_A$ カーネルは次のように与えられます $<m_A P_A + n_AQ_A>$ 。

ボブは同じアクションを実行しますが、同質性のみを構築します $<m_B P_B + n_BQ_B>$ 、カーネルとして選択されている場所 $<m_B P_B + n_BQ_B>$ 。

同質性 $\ phi_A$ そして $\ phi_B$ 秘密であり、誰にも渡されません。ただし、ボブとアリスの両方は、結果を何の影響も伴わずに同値曲線に分割できます。また、曲線自体を転送することもできます。これが実際に起こることです。この段階は、図の破線で示されています。アリスはポイントをボブに渡す $\ phi_A（P_B）$ そして $\ phi_A（Q_B）$ 、および曲線自体 $E_A$ 。ボブも同じことをします：アリスにポイントを渡します $\ phi_B（P_A）$ そして $\ phi_B（Q_A$ と曲線 $E_B$ 。

これはまったく合法ですか？！落ち着いて、 ％username％ 、両方の同質遺伝子曲線を知っていると、攻撃者は同質遺伝子自体を計算できなくなります。

それで、アリスとボブはデータを交換しました。今、私たちは最終的で信じられないほど美しいステージ、つまり、共通キーの取得に近づいています。ポイントの画像を知る $P_A$ そして $Q_A$ 曲線上 $E_B$ および乱数 $m_B$ そして $n_B$ ボブは簡単に同質性を構築できます $\ phi'_A$ 、そして同じ量の情報を持っているアリスは同質性を構築することができます $\ phi'_B$ 。エレガントなソリューションは、その同質性です $\ phi'_A$ そして $\ phi'_B$ 対談者を曲線に導く $E_ {AB}$ 、そしてそれはキーとして取ることができます $j-$ 不変。

マイクロソフトは、アルゴリズムの上記のステップを自由にコーディングする基本機能を実装することにより、人生を大幅に簡素化しました。キー分離スキームを実装する前に、暗号化システムのパラメーターを含む構造を初期化する必要があります。

CurveIsogeny = SIDH_curve_allocate(CurveIsogenyData); if (CurveIsogeny == NULL) { Status = CRYPTO_ERROR_NO_MEMORY; goto cleanup; } Status = SIDH_curve_initialize(CurveIsogeny, &random_bytes_test, CurveIsogenyData); if (Status != CRYPTO_SUCCESS) { goto cleanup; }

構造自体：

 typedef struct { CurveIsogeny_ID CurveIsogeny; unsigned int pwordbits; unsigned int owordbits; unsigned int pbits; uint64_t prime[MAXWORDS_FIELD]; uint64_t A[MAXWORDS_FIELD]; uint64_t C[MAXWORDS_FIELD]; unsigned int oAbits; uint64_t Aorder[MAXWORDS_ORDER]; unsigned int oBbits; unsigned int eB; uint64_t Border[MAXWORDS_ORDER]; uint64_t PA[2*MAXWORDS_FIELD]; uint64_t PB[2*MAXWORDS_FIELD]; unsigned int BigMont_A24; uint64_t BigMont_order[BIGMONT_MAXWORDS_ORDER]; uint64_t Montgomery_R2[MAXWORDS_FIELD]; uint64_t Montgomery_pp[MAXWORDS_FIELD]; uint64_t Montgomery_one[MAXWORDS_FIELD]; } CurveIsogenyStaticData;

アリスとボブがキーを交換するには、「フードの下」で何が起こっているのかを知る必要がない関数をいくつか呼び出すだけで十分です。キー生成は、次の機能を使用して行われます。

 Status = KeyGeneration_A(PrivateKeyA,PublicKeyA, CurveIsogeny);

そして

 Status = KeyGeneration_B(PrivateKeyB,PublicKeyAB CurveIsogeny);

アリスとボブは計算された公開鍵を交換し、共通鍵を見つけます：

 Status = SecretAgreement_A(PrivateKeyA, PublicKeyB, SharedSecretA, false, CurveIsogeny);

そして

 Status = SecretAgreement_B(PrivateKeyB, PublicKeyA, SharedSecretB, false, CurveIsogeny);

ライブラリ内の関数の中で、基本的な算術を区別できます。これは、プロトコルの実装に役立ちます。これは、たとえば、j_inv、楕円曲線のj不変量の計算、inv_3_way、乗法的逆数の値の検出、ポイントの倍増とポイントの追加-xDBLADD、ポイントの3倍-xTPLなどです。詳細な説明は、出版物に記載されています。

6.コーディングの時間です！

根拠がなく、量子後暗号化に直面して明るい未来に触れないようにするために、比較的限られた電力のデバイス、つまり携帯電話の例でこのライブラリの適用性をテストすることにしました。その結果、投票アプリケーションがAndroid OSに実装されました。そのチップは、デバイスで送信された音声を暗号化し、サーバーで復号化するためのポスト量子暗号化の導入です。

暗号化自体は、ライブラリの名前が示すとおり、そこでは実装されていないため、出版物を武器に暗号化スキームを実装しました。最終的なプロトコルは、元のプロトコルと大差ありません。

だから、私たちはよく知られた曲線を持っています $E_0$ それと同じ4つのポイント $P_A、Q_A、P_B、Q_B$ 、2つの量子妄想とコミュニケーションへの強い欲求。暗号システムのパラメーターで構造を初期化します。

 CurveIsogeny = SIDH_curve_allocate(CurveIsogenyData); Status = SIDH_curve_initialize(CurveIsogeny, &random_bytes_test, CurveIsogenyData);

ここでの公開鍵は、値のタプルとして表されます。 $E_A、\ phi_A（P_B）、\ phi_A（Q_B）$ 乱数 $k$ 。秘密鍵は数字で表されます $m_A$ そして $n_A$ 同質性が構築されるの助けを借りて $\ phi_A：E_0 \右矢印E_A$ 。

 Keys.PrivateKey = (unsigned char*)calloc(1, obytes); Keys.PublicKey = (unsigned char*)calloc(1, 4 * 2 * pbytes); random_bytes_test(10, Keys.k); Status = KeyGeneration_A(Keys.PrivateKey, Keys.PublicKey, CurveIsogeny);

暗号化ステップ中に、ボブはランダムな値を生成します。 $m_B$ 、 $n_B$ 同質性を構築します $\ phi_B：E_0 \右矢印E_B$ 。渡された公開キー値を使用する $E_A、\ phi_A（P_B）、\ phi_A（Q_B）$ ボブの建物の同質性 $\ phi'_B：E_A \右矢印E_ {AB}$ 共通の曲線に入ります。

 Status = KeyGeneration_B(IsogenyB, imagesB, CurveIsogeny); Status = SecretAgreement_B(IsogenyB, PublicKey, j, false, CurveIsogeny);

さらに吐き出すことができます。 $j-$ 一般曲線の不変量 $E_ {AB}$ 数字と連結します $k$ 、およびこのハッシュからハッシュが取得されます。取得した値は秘密データと矛盾しています。アプリケーションの場合、これはレポートのタイトルからのハッシュです。

 strncat(j, k, 10); shaCompute(j, hash); for (i = 0; i < strlen(message); i++) message[i] ^= hash[i];

アリスは値のタプルを受け取ります $E_B、\ phi_B（P_A）、\ phi_B（Q_A）$ および暗号文の値。彼女は同質性を構築するデータによると $\ phi'_A$ 共通の曲線に入る $E_ {AB}$ そして彼女を使用して $j-$ 不変、メッセージを解読します。

 Status = SecretAgreement_A(PrivateKey, imagesB, j, false, CurveIsogeny); strncat(j, k, 10); shaCompute(j, hash); for (i = 0; i < strlen(cipher); i++) cipher[i] ^= hash[i];

アプリケーションが起動すると、リクエストがサーバーに送信され、それに応答してレポートのリストが送信されます。ユーザーが投票する場合（対応するボタンを押すことで）、サーバーは音声の暗号化に必要なオープンパラメーターを送信します。クライアントは、それを失うことなく、これらのパラメーターを使用し、約5〜8秒考えて、復号化と暗号化テキストに必要なパラメーターを送信します。サーバーは約0.11秒でこのビジネスを解読し、クライアントに投票結果を提供します。

JavaとCの「友達を作る」ために、JNIテクノロジーが使用されました。 SIDHはライブラリにコンパイルされ、Javaコードで接続されます。

 static { System.loadLibrary("native-lib"); }

開発されたアプリケーションは、NeoQUEST Face-to- Face 2017年6月29日にダウンロードできます。多くの学生がこの機会を利用して、暗号化の分野で将来の方向性を検討し、気に入った報告書に投票しました。さらに、すべての音声は量子コンピューターへの攻撃から保護されていました！まあまだ-アプリケーションは美しいです！

そして結論として...

もちろん、実際には強力な量子コンピューターが存在しない場合でも、ポスト量子暗号の必要性を判断することは依然として困難です。しかし、NSAとNISTの大騒ぎは疑いを招かざるを得ません。そのような急ぎの本当の動機についてのみ推測できます。いずれにせよ、特に実際に実行可能な場合は、安全にプレイして、暗号化の新しい興味深い方向を探り始めることは決して痛いことはありません。

アプリケーションの実装に興味があり、何か新しいものを書きたい場合は、ソースへようこそ！

まもなく、 YouTubeチャンネルにNeoQUEST-2017 Face-to-Face Reportのビデオレポートを投稿します。これには、とりわけ楕円曲線とポスト量子暗号に関するレポートが含まれます。

さて、 VKのNeoQUESTグループに NeoQUEST-2017の写真をすでに投稿しています。近い将来、ハッククエストの割り当て（対立のゲストの目から隠されている）を含む新しい記事を期待してください！

量子後暗号と日没RSA-本当の脅威か想像上の未来か？