
何かまたは誰かを管理することは、原則として、管理対象システムに絶えず影響を与えません。 最終的に目的の目標が達成されるように調整することを試みます。 努力が必要な時期と場所を迅速に決定すると、システムは開発の計画ベクトルからわずかに離れ、最小限のコストで必要な目標への道に戻ります。
修正が必要なシステムの要素をすばやく見つける方法 今日はこの質問に答えようとします。

複雑なアルゴリズムの分野で解決策を模索することはありません。複雑なアルゴリズムは、理解して適用することが難しい場合があります。 約70年前に、国全体の危機を克服する理由であった簡単なことについてお話します。 質量現象の測定と分析について説明します。 そのような現象のみが統計的に制御されます。 なぜ人々は統計を悪とみなすことができるのでしょうか? これは、意図または愚かな人がそれに基づいて誤った結論を出すという事実が原因である場合があります。 多くの人が日常生活で直面する3つの例。
平均値は氷山の一角です
2つの異なる母集団からの50のボリュームを持つ2つのサンプルの平均値を考慮します。 偶然に、彼らは一致しました。 そして、それは平均が私たちに示すものをよく説明します。それはシステムの簡単な説明に非常によく使われます。 州のすべての従業員または市民の収入をリストする代わりに、彼らは平均値について話している。 そして、我々が理解したように、平均値は異なる母集団で同じかもしれません。 また、同じシステムでも異なる時点で同じになる場合があります。 たとえば、州の市民の収入の例では、中産階級の規模の増加が起こり、富裕層の富の増加と貧困層の収入の大幅な減少が起こる可能性があります。 したがって、システムをよく理解するには、このシステムでの量の分布の法則を知る必要があります。
さらに観察が必要
第二に、統計的研究の基礎は、1つ以上の特徴の測定に関する多くのデータです。 ランダム値の一連の観測によって統計的に表されるオブジェクトの実際の観測可能なコレクションは、サンプルです。 仮説的に存在する(想像される)-一般集団による。 サンプルサイズが十分に大きい場合(n→∞)、サンプルは大きいと見なされます。それ以外の場合は、サイズが制限されたサンプルと呼ばれます。 そのため、1次元のランダム変数を測定する際にサンプルサイズが30(n <= 30)を超えず、多次元空間で複数(k)の特徴を同時に測定する場合、nとkの比が10(n / k <10 ) 小さなサンプルの統計を分析する場合、統計計算には大きな誤差があることを理解する必要があります。
「できません!」
第三に、 統計は特定の1つのケースについては何も言っていません。 マーチンゲールシステムでコイントスをプレイするとします。 ワシまたは尾が落ちる確率は1/2であることを知っています。 あなたには15,000ルーブルがあり、それぞれ1,000ルーブルを賭けることにしました。 「ワシ」の損失に常に1000ルーブルを賭けます。 勝ちの場合、1000ルーブルの賭けから再び始め、負けの場合、勝つまで毎回賭けを2倍にします。 しばらくすると、あなたは億万長者になるでしょう。 しかし、このシステムに従ってプレーすると、プレーヤーは利点を受け取らず、勝ち金を再分配するだけです。プレーヤーはめったに負けず、多くを失い、しばしばわずかに勝ちます。 あなたは不運だったし、尾が4回連続で落ちました。 そのような結果の確率は、0.5 * 0.5 * 0.5 * 0.5 = 0.0625です。
これは、4回のコインフリップでの100回の実験で6回以上です。なぜあなたのケースは6つではないのでしょうか? 統計では、0.0625では十分ではなく、幸運なことに、4コインを投げる無限の大規模な実験シリーズについて語っています。 確率論における多数の法則は 、固定分布からの十分に大きな有限サンプルの経験的平均(算術平均)は、この分布の理論的平均(数学的な期待値)に近いと述べています。 つまり、一連の実験が大きくなるほど、これらの実験の結果は計算された確率(この場合は0.0625)に近くなります。 しかし、有限で少数の実験がある場合、結果は任意になります。 言い換えれば、同じスキームに従ってすぐに15,000でプレイしようとすると、次の損失はコイントスの結果の可能な分布に収まります。 2回の4回のトスの結果としての2つの損失の組み合わせは、はるかに少ないことに注意してください。 0.0625 * 0.0625 = 0.00390625または1000回の実験あたり約4回(2回の4回のトスから)。 そのような確率はすでにゲームの誠実さを考える機会ですが、そのような結果が可能なため、不正の唯一の証拠となることはできません。
練習に移りましょう
これらの例はすべて、統計の防御だけでなく、統計的に制御されたシステムの指標の正しい分析を支援する目的でも提供されています。 この場合の管理対象システムの例は、20人の専門家がいる技術サポート部門です。 理解を容易にするために、それらは完全にロードされていると仮定し、異なるクライアントで発生するあらゆるタイプの問題を解決します。 さまざまなタイプの問題の解決に、ほぼ同じ時間が費やされます。 月末には、次の結果が得られました。 これらは昇順または降順でソートされ、多くのマネージャーの結論の基礎となります。
| 場所 | スペシャリスト | 合計ヒット数、PC | チケットあたりの平均時間、分 |
| 1 | イワノフ | 246 | 39 |
| 2 | ペトロフ | 240 | 40 |
| 3 | チカロフ | 234 | 41 |
| 4 | フェドトフ | 228 | 42 |
| 5 | マキシモフ | 222 | 43 |
| 6 | コロレフ | 222 | 43 |
| 7 | フロロフ | 222 | 43 |
| 8 | チェルノフ | 216 | 44 |
| 9 | ベロフ | 216 | 44 |
| 10 | アントノフ | 216 | 44 |
| 11 | グリゴリエフ | 216 | 44 |
| 12 | トカチェンコ | 210 | 46 |
| 13 | クズネツォフ | 204 | 47 |
| 14 | ロマノフ | 204 | 47 |
| 15 | スミルノフ | 204 | 47 |
| 16 | ヴァシリエフ | 204 | 47 |
| 17 | ノヴィコフ | 198 | 48 |
| 18 | ヤコブレフ | 192 | 50 |
| 19 | ポポフ | 190 | 51 |
| 20 | フェドロフ | 142 | 69 |
部門の長が給与の20%の割合でTOP-3の管理職にボーナスを与えることを決定し、20%の最悪の結果で3人の専門家に罰金を科すと仮定します。 モチベーションの問題を解決するのは正しいですか? 部門の責任者は、最悪の事態に陥らないように、従業員がより良い結果を目指して努力するインセンティブを提供したいという願いで彼の決定を説明しています。 リストの最後から3人の専門家が選ばれたのはなぜですか? おそらくこれは部門長のお気に入りの番号だからです。
統計を使用するとどうなりますか?
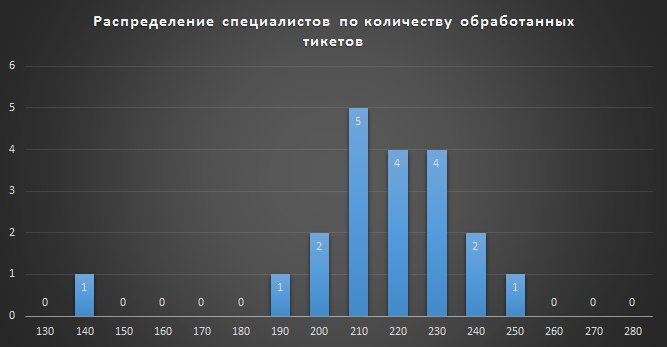
これは、処理されたコールの数によるスペシャリストの分布密度のようです。 19人の専門家がサンプルを形成し、その指標は正規分布によって十分に説明されることが明らかに見られます。
観測の結果が多くのランダムな弱相互依存量の合計であり、それぞれが合計に対して小さな寄与をする場合、項の数が増えると、中心化され正規化された結果の分布は正規になります。 この確率論の法則は、正規分布が広く分布していることの結果であり、その名前の理由の1つとなっています。
統計と確率理論の観点からこれはどういう意味ですか? 19名の専門家がうまく働いた。 多くの現象(ノイズ、室温、気分など)があり、それぞれが専門家に異なる程度の影響を与え、結果の実際の分布に至りました。 リストの最初のものは、彼らがうまくしたい19番目のものよりもうまくいったと言うことは可能ですか? この場合の統計は、彼らの仕事の結果の違いは、ランダムな理由によって引き起こされる可能性があると言っています。 運や失敗は従業員の収入に変化をもたらすべきですか? 私の意見では、いいえ。 その結果、従業員は費やされた努力と得られた結果との関係を感じません。 これにより、作業効率を高めるための追加のインセンティブを作成できません。
20人目の従業員(フェドロフ)はどうですか? システム内の従業員の結果が正規分布しているという仮説を受け入れた場合、そのようなシステムで結果が得られる可能性が認識されます。 フェドロフは140枚のチケットを処理しました。 正規分布下、つまり、同じランダム要因の多くが組み合わさった影響下でのそのようなイベントの確率は、10,000回の実験のうち1回です。 私たちには2つの選択肢があります:フェドロフはひどく不運だった、または彼の結果に影響したいくつかの特別な理由 (仕事への抵抗を含む)がありました。
従業員の結果が適合するフレームワークへの逸脱はどれほど敏感であり、特定のルールに従って誰もが自分で選択できます。 Shekhart-Deming管理図の原則によれば、管理境界は値がプロセスの安定した(通常の)状態にある廊下です。
Shekhartコントロールカードを作成する目的は、プロセスの安定状態からの脱出のポイントを特定し、その後に発生した逸脱の原因を特定して解消することです。 デミングのおかげで大部分は6シグマ方式です。
メソッド名は、ギリシャ文字σで示される標準偏差の統計的概念に基づいています。 この概念におけるプロセスの成熟度は、出力インジケータが正規分布の密度の99.99966%に適合するシステム要素の割合として説明されます。 この方法で制御するためには、どの制御境界を取るかを理解することが重要です。 どのくらいの確率で、異常、または管理図の観点から、プロセスの「外れ値」を考慮するのでしょうか? 一般的な標準プラクティスは、算術平均からの3つの標準偏差です。 なぜ8または4ではなく6シグマですか? 便利で快適な3を掛けることができますが、主なことは、分布の本当に小さな部分が±3シグマの限界を超えて残っていることです。 平均値からの偏差は、上側の制御境界を受け取って加算するか、下側の制御境界を取得するために減算できることは明らかです。
テクニカルサポート部門の架空の結果のコントロールカードを作成します。
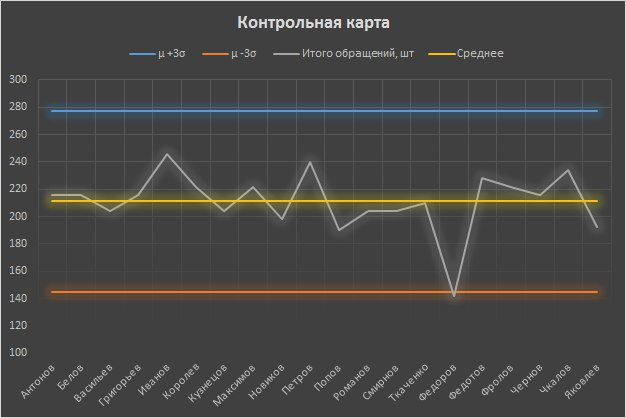
確かに、フェドロフはコントロールの境界内に収まらない異常な結果を示しました。 上司は彼にインタビューした後、この結果の理由を見つけ、これらの理由の妥当性に応じて従業員の動機を決定する必要があります。 残りの従業員の結果は通常分布していました。つまり、統計の観点からは、多くのランダムな要因の影響を受けていました。 労働者のいずれかが上位管理境界の外側で顕著な結果を示す場合、この現象はより大規模な実施の可能性に関する研究も必要とするでしょう。
ただし、月末に従業員の動機を決定することは最良の決定ではありません。 過去には、変更することは不可能ではありませんし、個々の従業員の悪い結果は部門全体の仕事の結果に影響を与える可能性があります。 システム開発ベクトルを時間内に応答して調整するには、さらに管理図が必要です。 従業員ごとにそれらを持ち、観測を毎日記録していると想像してください。
Fedorovの制御カードを見てみましょうが、まず、プロセスの安定性(制御性)の違反とこの変動の特別な理由の出現を示す、特定のプロセス変動の兆候について少し説明しましょう。
- コントロールカードの上限または下限を超える出口ポイント
- 行の7つ以上のポイントが正中線の片側にある
- 6ポイントを超える単調増加または単調減少
他の兆候があります。 管理図を読み取るための確立された一般に認められた追加のルールのセットはありません。したがって、まずシュハルトルール(国境を越えたポイントの出口)を使用し、必要に応じて経験が得られたら他のすべてを導入することをお勧めします。
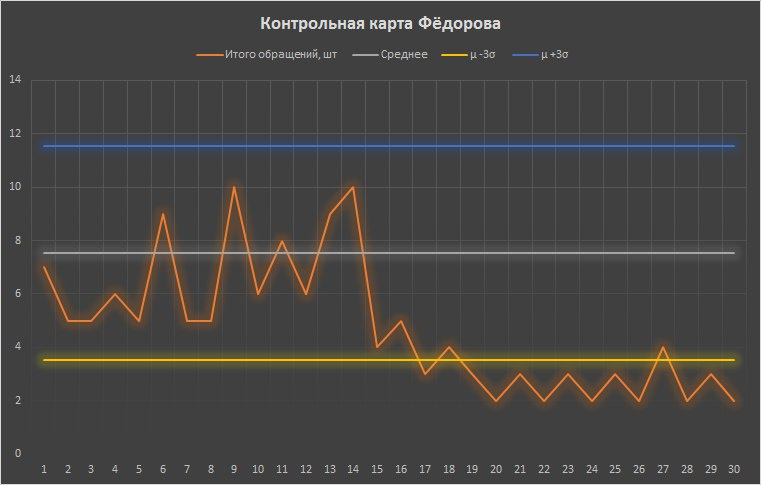
フェドロフの仕事が変わったことに留意するために、月末だけでなく可能になりました。 すでに17日に、コントロールの境界を越えてインジケーターのリリースがありました。 この瞬間に、部門の長が信号に気付き、この異常の原因を突き止めることになりました。
一般に、これは品質管理のトピックです。 その目的は、販売プロセス、人事管理、サービスの提供、製品の生産など、あらゆるプロセスの安定性(制御可能性)を確保することです。 実数の例を示します。 クラウドプロバイダーとして、 SLAサービスの可用性が99.95%以上であることを確認する必要があります。 つまり、特定のインフラストラクチャ(特定の特性を備えた仮想マシンなど)またはサービス(仮想デスクトップなど) は 、1か月に22分以内しかクライアントから利用できない場合があります。 クラウドプロバイダーがサービスを提供するプロセスの出口のこのような信頼性と安定性を確保するために、安定したシステムが構築されており、前の例よりもはるかに高い頻度で監視されています。 このようなシステムの中心となるのは、複数のTier IIIデータセンターにあるエンタープライズクラスの機器であり、重複したチャネルを備えた高可用性の光リングで接続されています。 クラウドプロバイダーのビジネスは、サービスの品質がコンピューターシステムと組織の人員の品質に依存する場合の主要な例の1つです。
統計的プロセス管理のトピックが気に入ったら、エドワーズデミングの本「危機の克服:人、システム、プロセスを管理するための新しいパラダイム」を読むことを強くお勧めします。 デミングは1946年に最初に戦争で荒廃した日本を訪れました。 統計的品質管理方法に関する彼の講義は、日本企業の上級管理職によって受けられました。 統計的制御方法を研究し、実施する必要性が認識され、日本では管理職の大規模なトレーニングのプロセスが組織されました。 これらの方法のさらなる開発は、タオトヨタシステムとカイゼン哲学の創造につながりました。 多くの人々は、これらの方法が「日本の経済的奇跡」の原因であると考えており、それがこの国を経済リーダーに導いた。 この記事を書くきっかけとなった「危機を克服する」という本からの引用がいくつかあります。
「このシステムに属する人々のランク付けは(傑出したものから最悪のものまで)科学的論理に反し、政治家として破壊的です。」
「管理者は、関連データがある場合は計算を使用して、またはそのようなデータがない場合は判断に基づいて、システムの外部にいる従業員をより良くも悪くも区別できるため、特別な支援が必要です。または、何らかの形で強調して奨励する必要があります。