飛行機の可視化を備えたリトルのアルゴリズムで巡回セールスマン問題を解決する

少なくとも19世紀以来知られている巡回セールスマン問題には多くの解決策があり、繰り返し説明されてきました。 最適化バージョンはNPハードなので、最適なソリューションは、網羅的検索または最適化された網羅的検索（分岐限定法を使用）によって取得できます。

Littleアルゴリズム（分枝限定法の特殊なケース）をプログラムしようとすると、Runetでは、理解可能な言語と逆アセンブルされたソフトウェア実装で正しい記述を見つけることは非常に難しいことに気付きました。 ただし、豊富な説明は小さなデータでは一見妥当であり、視覚化せずに検証することは困難です。

枝とボーダーの方法

ほとんどのアルゴリズムはMViGの特殊なケースです。 最悪の場合、その複雑さは徹底的な検索の複雑さに等しい。 理論的な説明は次のとおりです。

ラフのすべてのハミルトニアンサイクルの集合Sがあります。 Sの各ステップで、エッジ（i、j）が求められ、ルートから除外すると下限が最大になります。 次に、セットは2つの独立したS1とS2に分割されます。 S1-エッジを含む（i、j）および含まない（j、i）すべてのサイクル。 S2-（i、j）を含まないすべてのサイクル。 次に、各セットのパスの長さの下限が計算され、すでに見つかった解の長さを超える場合、セットは破棄されます。 そうでない場合、セットS1およびS2はSと同じ方法で処理されます。

アルゴリズムの説明

距離行列Mがあります。対角要素は無限値で満たされています。 早すぎるサイクルは発生しません。 下限を格納する変数もあります。

2種類の無限大を追跡する必要があることに言及する価値があります。1つは行列から行と列を削除した後に追加され、早期ループが発生しないようにするものと、エッジを破棄するものです。 ケースは少し後で検討されます。 最初の無限大はinf1で示され、2番目の無限大はinf2で示されます。 対角線はinf1で埋められます。

1. 各行の各要素から、この行の最小要素が差し引かれます。 この場合、最小の行要素が下限に追加されます
2. 各列から、最小要素が同様に減算され、下限に追加されます。
3. 各ゼロ要素M（i、j）について、要素（i、j）自体を除く、行iと列jの最小要素の合計に等しい係数が計算されます。 この係数は、エッジ（i、j）を除外する場合、解の下限をどのように増加させることが保証されるかを示します。
4. 最大係数を持つアイテムが検索されます。 それらが複数ある場合は、いずれかを選択できます（とにかく、残りは再帰の次のステップで考慮されます）
5. M1とM2の2つの行列を考えます。 M1はMに等しく、行iと列jが削除されています。 列kと行lが含まれ、これらにはinf1は含まれず、要素M（k、l）はinf1に相当します。 前述したように、これは時期尚早のサイクル（つまり、最初の段階（k、l）==（j、i））を回避するために必要です。 行列M1は、エッジ（i、j）を含むセットに対応します。 列と行の削除とともに、エッジ（i、j）がパスに含まれます。
6. M2は行列Mに等しく、要素（i、j）はinf2に等しくなります。 マトリックスは、エッジ（i、j）を含まないパスのセットに対応します（エッジ（j、i）が除外されないことを理解することが重要です）。
7. 行列M1およびM2の手順1に進みます。

ヒューリスティックは、マトリックスM1の下限はマトリックスM2以下であり、最初にエッジ（i、j）を含むブランチが考慮されることです。

例

インターネットには多くの例がありますが、本当に興味深いのは、 この記事ではよく説明されているツリーです（私が見つけた唯一の記事でもあり、一般的なエラーを示していますが、残念ながら、アルゴリズムのアルゴリズム記述が不十分です-最初にマトリックスについて、次にセットについて） ） 興味深い例は、ペナルティが最大のエッジを持つブランチのみを考慮すると、誤った結果が得られることです。

そこで、このマトリックスの最適なパスを見つける手順を説明します。

	0	1	2	3	4
0	inf	20	18	12	8
1	5	inf	14	7	11
2	12	18	inf	6	11
3	11	17	11	inf	12
4	5	5	5	5	inf

実装

ステップ1

各行と各列でゼロを取得します。

 double LittleSolver::subtractFromMatrix(MatrixD &m) const { //     double subtractSum = 0; //        vector<double> minRow(m.size(), DBL_MAX), minColumn(m.size(), DBL_MAX); //    for (size_t i = 0; i < m.size(); ++i) { for (size_t j = 0; j < m.size(); ++j) //      if (m(i, j) < minRow[i]) minRow[i] = m(i, j); for (size_t j = 0; j < m.size(); ++j) { //      //  ,   if (m(i, j) < _infinity) { m(i, j) -= minRow[i]; } //         if ((m(i, j) < minColumn[j])) minColumn[j] = m(i, j); } } //      //  ,   for (size_t j = 0; j < m.size(); ++j) for (size_t i = 0; i < m.size(); ++i) if (m(i, j) < _infinity) { m(i, j) -= minColumn[j]; } //    for (auto i : minRow) subtractSum += i; for (auto i : minColumn) subtractSum += i; return subtractSum; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ステップ2

下限を増やして、レコードと比較します。

 //       //    bottomLimit += subtractFromMatrix(matrix); //      if (bottomLimit > _record) { return; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ステップ3

係数の計算。

 double LittleSolver::getCoefficient(const MatrixD &m, size_t r, size_t c) { double rmin, cmin; rmin = cmin = DBL_MAX; //     for (size_t i = 0; i < m.size(); ++i) { if (i != r) rmin = std::min(rmin, m(i, c)); if (i != c) cmin = std::min(cmin, m(r, i)); } return rmin + cmin; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

すべてのゼロ要素を検索し、それらの係数を計算します。

 //     list<pair<size_t, size_t>> zeros; //    list<double> coeffList; //   double maxCoeff = 0; //    for (size_t i = 0; i < matrix.size(); ++i) for (size_t j = 0; j < matrix.size(); ++j) //    if (!matrix(i, j)) { //     zeros.emplace_back(i, j); //       coeffList.push_back(getCoefficient(matrix, i, j)); //    maxCoeff = std::max(maxCoeff, coeffList.back()); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ステップ4

非最大係数のゼロ要素を破棄します。

 { //    auto zIter = zeros.begin(); auto cIter = coeffList.begin(); while (zIter != zeros.end()) { if (*cIter != maxCoeff) { //    ,     zIter = zeros.erase(zIter); cIter = coeffList.erase(cIter); } else { ++zIter; ++cIter; } } } return zeros;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ステップ5

ペナルティが最大のエッジを含むセットに移行します。

 auto edge = zeros.front(); //   auto newMatrix(matrix); //      ,    newMatrix.removeRowColumn(edge.first, edge.second); //  iter    auto newPath(path); newPath.emplace_back(matrix.rowIndex(edge.first), matrix.columnIndex(edge.second)); //       addInfinity(newMatrix); //  ,   edge handleMatrix(newMatrix, newPath, bottomLimit);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ステップ6

最大ペナルティを持つエッジを含まないセットへの移行。

 //   ,    edge //      newMatrix = matrix; //     iter newMatrix(edge.first, edge.second) = _infinity + 1; //  ,    edge handleMatrix(newMatrix, path, bottomLimit);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

MViGと網羅的検索の比較

最悪の場合、分枝限定法は徹底的な検索よりも優れているという事実にもかかわらず、ほとんどの場合、初期解を見つけ、明らかに悪いセットを破棄するためのヒューリスティックのおかげで、時間内に大幅に勝ちます。

以下は、MViGを徹底的な検索と、異なる数の都市で実装したアルゴリズムの平均実行時間を比較したグラフです。 ランダムに生成されたポイントのマトリックスでテストされています。

分枝限定法と徹底的な検索の比較。

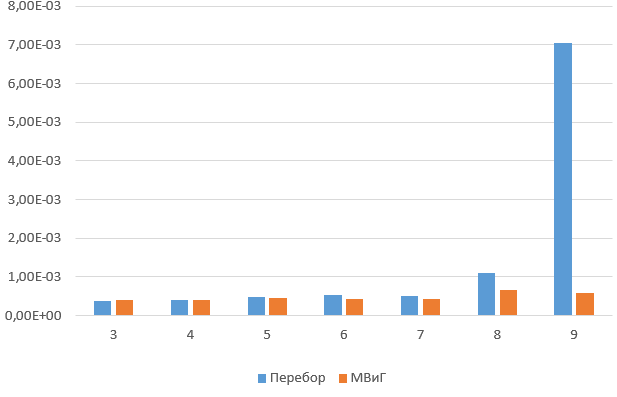
9つの都市から始めて、徹底的な検索はMViGで著しく失われます。 13都市から開始して、完全な検索には1分以上かかります。

異なる数の都市でのMViGの稼働時間。

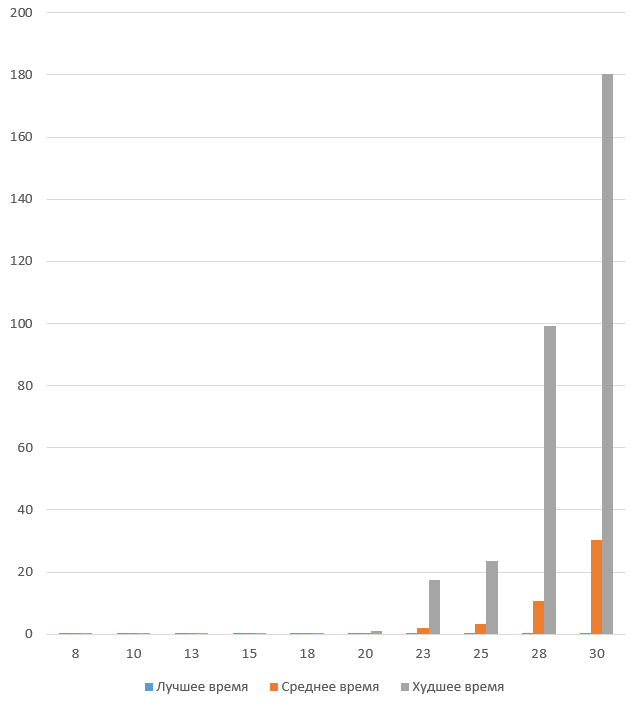
グラフィカルアプリケーション

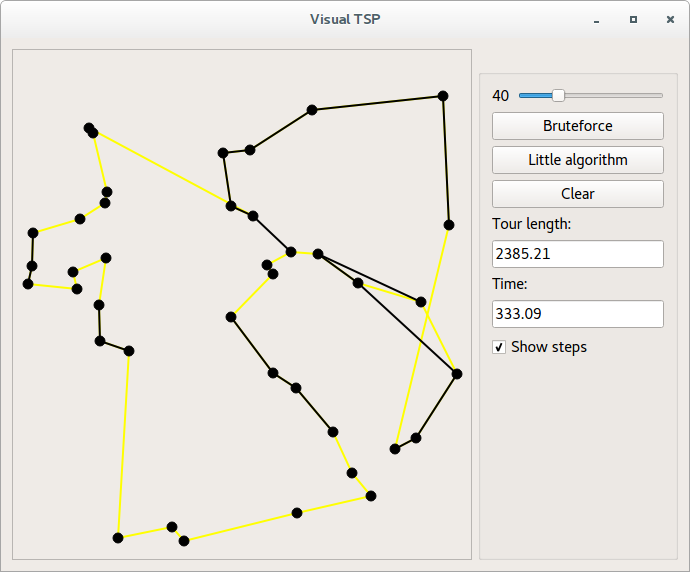
ソリューションプロセスを動的に確認する機能を備えたQtのグラフィカルインターフェイスも作成されました。 記事のヘッダーにあるgifのワークスペースだけです。 興味がある人は、プログラムをコンパイルして、自分の手で触ることができます。

黄色は、見つかった最適なパスを示し、その長さは[ツアーの長さ]フィールドにあります。

最後に表示されたセットのエッジは黒でマークされています。

動的表示の場合、タスクは、段階的に解決するか、グラフィカルインターフェイスと並行してスレッドで解決する必要があります。 なぜなら ソリューションの主な機能は再帰的であり、2番目のオプションが選択されました。そのため、決定的なクラスにミューテックスを追加し、レコード変数をアトミックにし、いくつかのメソッドでスレッドセーフを処理する必要がありました。

結論の代わりに

この記事が、このアルゴリズムを実装したい、または既に実装しているが、間違った結果を与える理由を理解していない人に役立つことを願っています。

→ ソースコード