内容
- パート1： はじめに
- パート2： 多様体学習と潜在変数
- パート3： 可変可変エンコーダー（ VAE ）
- パート4： 条件付きVAE
- パート5： GAN （Generative Adversarial Networks）とテンソルフロー
- パート6： VAE + GAN
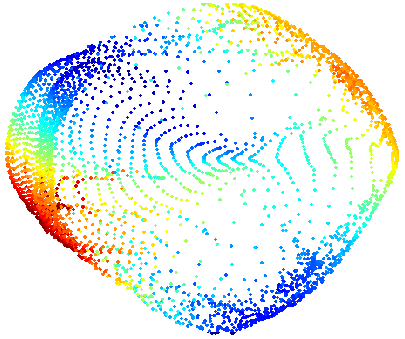
自動エンコーダーがどのように機能するかをよりよく理解し、その後コードから新しいものを生成するためには、コードが何であり、どのように解釈できるかを理解する価値があります。
マニホールド学習
mnist数字の画像（最後の部分の例）は要素です
-28 x 28のモノクロ画像のような次元空間。
ただし、すべての画像の中で、数字の画像はわずかな部分しか占めておらず、画像の絶対的な大部分は単なるノイズです。
一方、図形の任意の画像を撮影する場合、特定の近傍からのすべての画像も図形と見なすことができます。
そして、数字の2つの任意の画像を取得すると、おそらく元の784次元空間で、連続曲線を見つけることができます。それに沿ってすべての点が数字と見なされる可能性があります（少なくとも1つのラベルの数字の画像について）、そして前の発言と一緒に、それがすべてですこの曲線に沿ったいくつかの領域の点。
したがって、すべての画像の空間では、数字の画像が集中している領域に、より小さな次元の部分空間があります。 つまり、私たちの母集団が原則として描画できる数字の画像すべてである場合、その領域内でそのような数値を満たす確率密度は、外部よりもはるかに高くなります。
コードkの次元を持つ自動エンコーダーは、サンプル内のすべての変動を最も完全に伝えるオブジェクトの空間でk次元多様体を探しています。 そして、コード自体がこの多様性のパラメーター化を設定します。 この場合、エンコーダーはオブジェクトを多様体上のパラメーターにマッピングし、デコーダーはパラメーターをオブジェクトの空間内のポイントにマッピングします。
コードの次元が大きいほど、エンコーダが送信できるデータのバリエーションが多くなります。 コードの次元が小さすぎる場合、自動エンコーダーは、指定されたメトリックの欠落したバリエーションにわたって平均化されたものを記憶します（これは、自動エンコーダーのコード次元の減少に伴い、 mnist桁がぼやけている理由の1つです）。
多様体学習とは何かをよりよく理解するために、曲線とノイズの形式で単純な2次元データセットを作成し、その上で自動エンコーダーをトレーニングします。
コードと視覚化
# import numpy as np import matplotlib.pyplot as plt %matplotlib inline import seaborn as sns # x1 = np.linspace(-2.2, 2.2, 1000) fx = np.sin(x1) dots = np.vstack([x1, fx]).T noise = 0.06 * np.random.randn(*dots.shape) dots += noise # from itertools import cycle size = 25 colors = ["r", "g", "c", "y", "m"] idxs = range(0, x1.shape[0], x1.shape[0]//size) vx1 = x1[idxs] vdots = dots[idxs]
# plt.figure(figsize=(12, 10)) plt.xlim([-2.5, 2.5]) plt.scatter(dots[:, 0], dots[:, 1]) plt.plot(x1, fx, color="red", linewidth=4) plt.grid(False)
上の図では、青い点がデータであり、赤い曲線がデータを定義する多様性です。
線形圧縮オートエンコーダー
最も単純な自動エンコーダーは、線形アクティベーション機能を備えた2層の圧縮自動エンコーダーです（線形アクティベーションではより多くのレイヤーが意味をなしません）。
このような自動エンコーダーは、オブジェクトの空間でアフィン（シフトを伴う線形）サブスペースを検索します。これは、オブジェクトの最大の変動を表し、 PCA （プリンシパルコンポーネントメソッド）は同じことを行い、両方が同じサブスペースを検出します
from keras.layers import Input, Dense from keras.models import Model from keras.optimizers import Adam def linear_ae(): input_dots = Input((2,)) code = Dense(1, activation='linear')(input_dots) out = Dense(2, activation='linear')(code) ae = Model(input_dots, out) return ae ae = linear_ae() ae.compile(Adam(0.01), 'mse') ae.fit(dots, dots, epochs=15, batch_size=30, verbose=0)
# pdots = ae.predict(dots, batch_size=30) vpdots = pdots[idxs] # PCA from sklearn.decomposition import PCA pca = PCA(1) pdots_pca = pca.inverse_transform(pca.fit_transform(dots))
可視化
# plt.figure(figsize=(12, 10)) plt.xlim([-2.5, 2.5]) plt.scatter(dots[:, 0], dots[:, 1], zorder=1) plt.plot(x1, fx, color="red", linewidth=4, zorder=10) plt.plot(pdots[:,0], pdots[:,1], color='white', linewidth=12, zorder=3) plt.plot(pdots_pca[:,0], pdots_pca[:,1], color='orange', linewidth=4, zorder=4) plt.scatter(vpdots[:,0], vpdots[:,1], color=colors*5, marker='*', s=150, zorder=5) plt.scatter(vdots[:,0], vdots[:,1], color=colors*5, s=150, zorder=6) plt.grid(False)
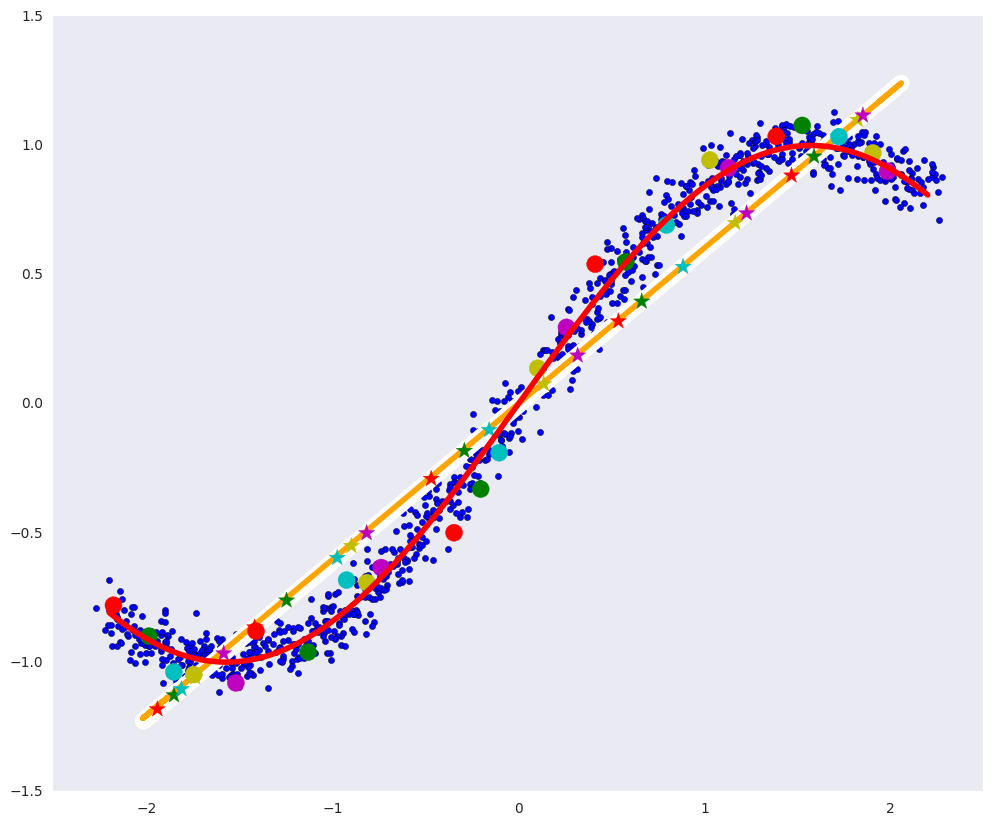
上の写真では：
- 白い線は、青いデータポイントがオートエンコーダの後に移動する種類です。つまり、オートエンコーダは、データのほとんどのバリエーションを定義する多様体を構築しようとします。
- オレンジ色の線は、PCAの後に青いデータポイントが移動する種類です。
- マルチカラーの円-自動エンコーダーの後、対応する色の星に変わるドット、
- マルチカラーの星-それぞれ、自動エンコーダー後の円の画像。
線形依存関係を探す自動エンコーダーは、データ内の任意の依存関係を見つけることができる自動エンコーダーほど有用ではない場合があります。 エンコーダとデコーダの両方が任意の関数を近似できる場合に役立ちます。 十分なサイズの少なくとも1つのレイヤーと、エンコーダーとデコーダーの間に非線形アクティベーション関数を追加すると、任意の依存関係を見つけることができます。
ディープオートエンコーダー
ディープオートエンコーダーには、より多くのレイヤーがあり、最も重要なこととして、それらの間に非線形活性化関数があります（この場合、 ELU-指数線形単位）。
def deep_ae(): input_dots = Input((2,)) x = Dense(64, activation='elu')(input_dots) x = Dense(64, activation='elu')(x) code = Dense(1, activation='linear')(x) x = Dense(64, activation='elu')(code) x = Dense(64, activation='elu')(x) out = Dense(2, activation='linear')(x) ae = Model(input_dots, out) return ae dae = deep_ae() dae.compile(Adam(0.003), 'mse') dae.fit(dots, dots, epochs=200, batch_size=30, verbose=0) pdots_d = dae.predict(dots, batch_size=30) vpdots_d = pdots_d[idxs]
可視化
# plt.figure(figsize=(12, 10)) plt.xlim([-2.5, 2.5]) plt.scatter(dots[:, 0], dots[:, 1], zorder=1) plt.plot(x1, fx, color="red", linewidth=4, zorder=10) plt.plot(pdots_d[:,0], pdots_d[:,1], color='white', linewidth=12, zorder=3) plt.plot(pdots_pca[:,0], pdots_pca[:,1], color='orange', linewidth=4, zorder=4) plt.scatter(vpdots_d[:,0], vpdots_d[:,1], color=colors*5, marker='*', s=150, zorder=5) plt.scatter(vdots[:,0], vdots[:,1], color=colors*5, s=150, zorder=6) plt.grid(False)
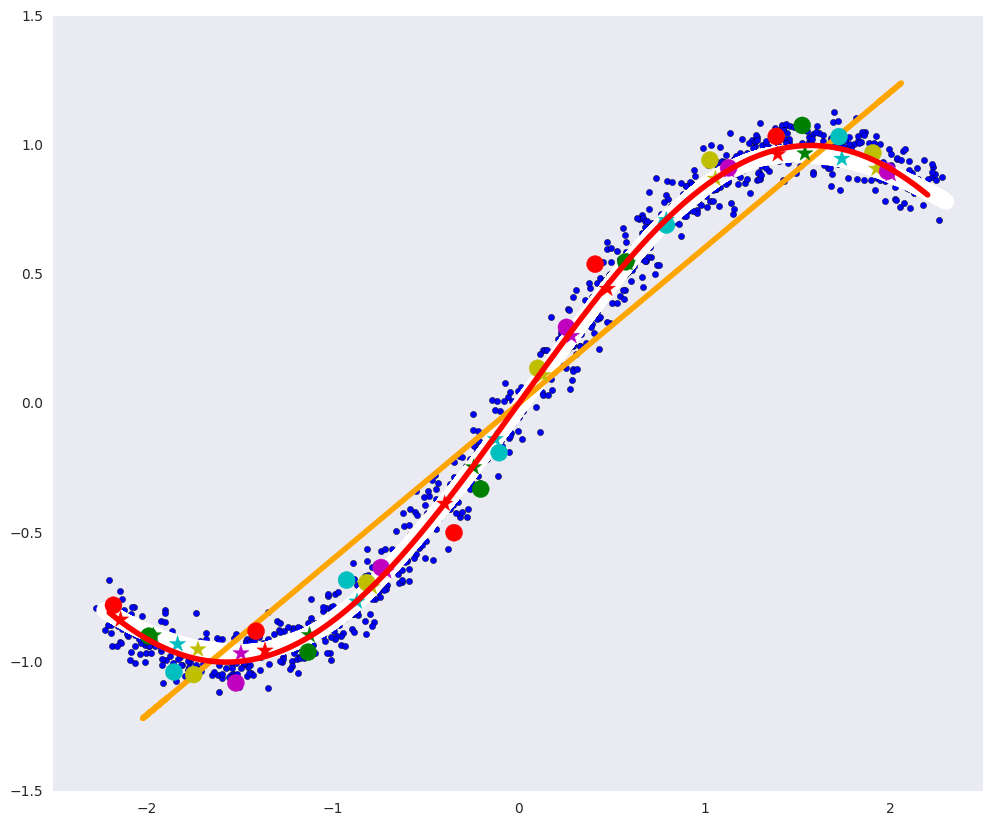
このような自動エンコーダーでは、明確な多様性を構築することはほぼ完全に可能でした。白い曲線はほとんど赤い曲線と一致しています。
ディープオートエンコーダーは、理論的には、任意の複雑さの集合体、たとえば、784次元空間に数が近くにある集合体を見つけることができます。
2つのオブジェクトを取り、それらの間の任意の曲線上にあるオブジェクトを見ると、一般的な母集団が存在する多様性は非常に湾曲している可能性が高いため、中間オブジェクトは一般的な母集団に属しません。
前のパートの手書きの数字のデータセットに戻りましょう。
まず、数字のスペースを8から別の8に直線的に移動します。
コード
from keras.layers import Conv2D, MaxPooling2D, UpSampling2D from keras.datasets import mnist (x_train, y_train), (x_test, y_test) = mnist.load_data() x_train = x_train.astype('float32') / 255. x_test = x_test .astype('float32') / 255. x_train = np.reshape(x_train, (len(x_train), 28, 28, 1)) x_test = np.reshape(x_test, (len(x_test), 28, 28, 1)) # def create_deep_conv_ae(): input_img = Input(shape=(28, 28, 1)) x = Conv2D(128, (7, 7), activation='relu', padding='same')(input_img) x = MaxPooling2D((2, 2), padding='same')(x) x = Conv2D(32, (2, 2), activation='relu', padding='same')(x) x = MaxPooling2D((2, 2), padding='same')(x) encoded = Conv2D(1, (7, 7), activation='relu', padding='same')(x) # (7, 7, 1) .. 49- input_encoded = Input(shape=(7, 7, 1)) x = Conv2D(32, (7, 7), activation='relu', padding='same')(input_encoded) x = UpSampling2D((2, 2))(x) x = Conv2D(128, (2, 2), activation='relu', padding='same')(x) x = UpSampling2D((2, 2))(x) decoded = Conv2D(1, (7, 7), activation='sigmoid', padding='same')(x) # encoder = Model(input_img, encoded, name="encoder") decoder = Model(input_encoded, decoded, name="decoder") autoencoder = Model(input_img, decoder(encoder(input_img)), name="autoencoder") return encoder, decoder, autoencoder c_encoder, c_decoder, c_autoencoder = create_deep_conv_ae() c_autoencoder.compile(optimizer='adam', loss='binary_crossentropy') c_autoencoder.fit(x_train, x_train, epochs=50, batch_size=256, shuffle=True, validation_data=(x_test, x_test)) def plot_digits(*args): args = [x.squeeze() for x in args] n = min([x.shape[0] for x in args]) plt.figure(figsize=(2*n, 2*len(args))) for j in range(n): for i in range(len(args)): ax = plt.subplot(len(args), n, i*n + j + 1) plt.imshow(args[i][j]) plt.gray() ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) plt.show() # def plot_homotopy(frm, to, n=10, decoder=None): z = np.zeros(([n] + list(frm.shape))) for i, t in enumerate(np.linspace(0., 1., n)): z[i] = frm * (1-t) + to * t if decoder: plot_digits(decoder.predict(z, batch_size=n)) else: plot_digits(z)
# frm, to = x_test[y_test == 8][1:3] plot_homotopy(frm, to)
コード間で曲線に沿って移動する場合（およびさまざまなコードが適切にパラメーター化されている場合）、デコーダーはこの曲線をコード空間からオブジェクトの空間で定義された多様性を残さない曲線に変換します。 つまり、曲線上の中間オブジェクトは母集団に属します。
codes = c_encoder.predict(x_test[y_test == 8][1:3]) plot_homotopy(codes[0], codes[1], n=10, decoder=c_decoder)
中間の数字は非常に良い8です。
したがって、オートエンコーダは、少なくともローカルで、定義多様体の形式を学習したと言えます。
自動エンコーダーの再トレーニング
オートエンコーダーがいくつかの複雑なパターンを分離する方法を学習するには、エンコーダーとデコーダーの一般化能力を制限する必要があります。そうしないと、1次元コードのオートエンコーダーでも、トレーニングセットの各ポイントで1次元曲線を簡単に描くことができます。 すべてのオブジェクトを覚えておいてください。 しかし、自動エンコーダーが構築するこの複雑な多様性は、一般集団を決定する多様性とあまり共通点はありません。
人工データで同じ問題を取り、非常に小さなポイントのサブセットで同じディープオートエンコーダーをトレーニングし、結果の多様体を見てください。
コード
dae = deep_ae() dae.compile(Adam(0.0003), 'mse') x_train_oft = np.vstack([dots[idxs]]*4000)
dae.fit(x_train_oft, x_train_oft, epochs=200, batch_size=15, verbose=1)
pdots_d = dae.predict(dots, batch_size=30) vpdots_d = pdots_d[idxs] plt.figure(figsize=(12, 10)) plt.xlim([-2.5, 2.5]) plt.scatter(dots[:, 0], dots[:, 1], zorder=1) plt.plot(x1, fx, color="red", linewidth=4, zorder=10) plt.plot(pdots_d[:,0], pdots_d[:,1], color='white', linewidth=6, zorder=3) plt.plot(pdots_pca[:,0], pdots_pca[:,1], color='orange', linewidth=4, zorder=4) plt.scatter(vpdots_d[:,0], vpdots_d[:,1], color=colors*5, marker='*', s=150, zorder=5) plt.scatter(vdots[:,0], vdots[:,1], color=colors*5, s=150, zorder=6) plt.grid(False)
白い曲線が各データポイントを通過し、データを定義する赤い曲線とわずかに似ていることがわかります。これは、顔の典型的な再訓練です。
非表示の変数
人口は何らかのデータ生成プロセスと考えることができます。
これは多くの隠された変数に依存します 
（ランダム変数）。 データ次元 隠れたランダム変数の次元よりもはるかに高くなる可能性があります これらのデータが決定します。 次の数字を生成するプロセスを検討してください。数字がどのように見えるかは、多くの要因に依存します。
- 希望の数
- ストローク太さ
- ティルト番号
- きちんとした
- など
これらの各要因にはそれぞれ固有の事前分布があります。たとえば、8の字が描かれる確率は1/10の確率のベルヌーイ分布です。ストロークの太さにもある程度の分布があり、精度と隠れた変数の両方に依存します。ペンの太さや人の気質（これもまた分布）。
学習プロセスでは、自動エンコーダー自体が、たとえば上記のような隠れた要因、それらのいくつかの複雑な組み合わせ、さらには完全に異なる要因に到達する必要があります。 ただし、彼が学習する共同分布は単純である必要はなく、何らかの複雑な曲線領域である可能性があります。 （この領域外からデコーダに値を渡すことができます。結果は、定義する多様体からではなく、そのランダムな連続拡張からのものになります）。
それが、私たちがただ新しいものを生成できない理由です
これらの隠された変数の分布から。 領域内にとどまることは難しく、この領域曲線の隠された変数の値を何らかの方法で解釈することはさらに困難です。
明確にするために、数値の例を使用して表記法を紹介します。
- -ランダムサイズの画像28x28、
- -絵の中の数字を決定する隠された要因のランダムな値、
-写真内の数字の画像の確率分布、すなわち 原則として、人物の特定の画像が描かれる確率（絵が数字のように見えない場合、この確率は非常に小さい）
-隠れた要因の確率分布、たとえば、ストロークの太さの分布、
-特定の画像の隠れた要因の確率分布（隠れた変数とノイズの異なる組み合わせが同じ画像につながる可能性があります）、
-与えられた隠された要因の画像の確率分布、同じ要因は異なる画像につながる可能性があります（同じ条件で同じ人が正確に同じ数字を描画しない）、
-共同配布 そして 、新しいオブジェクトの生成に必要なデータの最も完全な理解。
デコーダは私たちを近づけますが、 まだわかりません。
隠し変数が通常の自動エンコーダーでどのように分布しているか見てみましょう：
コード
from keras.layers import Flatten, Reshape from keras.regularizers import L1L2 def create_deep_sparse_ae(lambda_l1): # encoding_dim = 16 # input_img = Input(shape=(28, 28, 1)) flat_img = Flatten()(input_img) x = Dense(encoding_dim*4, activation='relu')(flat_img) x = Dense(encoding_dim*3, activation='relu')(x) x = Dense(encoding_dim*2, activation='relu')(x) encoded = Dense(encoding_dim, activation='linear', activity_regularizer=L1L2(lambda_l1, 0))(x) # input_encoded = Input(shape=(encoding_dim,)) x = Dense(encoding_dim*2, activation='relu')(input_encoded) x = Dense(encoding_dim*3, activation='relu')(x) x = Dense(encoding_dim*4, activation='relu')(x) flat_decoded = Dense(28*28, activation='sigmoid')(x) decoded = Reshape((28, 28, 1))(flat_decoded) # encoder = Model(input_img, encoded, name="encoder") decoder = Model(input_encoded, decoded, name="decoder") autoencoder = Model(input_img, decoder(encoder(input_img)), name="autoencoder") return encoder, decoder, autoencoder encoder, decoder, autoencoder = create_deep_sparse_ae(0.) autoencoder.compile(optimizer=Adam(0.0003), loss='binary_crossentropy')
autoencoder.fit(x_train, x_train, epochs=100, batch_size=64, shuffle=True, validation_data=(x_test, x_test))
n = 10 imgs = x_test[:n] decoded_imgs = autoencoder.predict(imgs, batch_size=n) plot_digits(imgs, decoded_imgs)
これは、このエンコーダーによって復元された画像がどのように見えるかです：
画像 
隠れ変数の共同分布
codes = encoder.predict(x_test) sns.jointplot(codes[:,1], codes[:,3])
共同分布が見られる
複雑な形状をしています。 
そして 
互いに依存しています。
隠し変数の分布を制御する方法はありますか
？
最も簡単な方法は、レギュラーを追加することです
または 
値へ 、これは、ラプラスまたは正規の隠れ変数の分布にそれぞれ先験的仮定を追加します（正則化中に重みの値に追加された先験的分布と同様）。
レギュラライザーは、自動エンコーダーに、必要な法則に従って配布される隠し変数を探すように強制します。成功するかどうかは別の質問です。 しかし、これはそれらを独立させることを強制するものではありません。
。
スパースオートエンコーダーの隠れたパラメーターの共同分布を見てみましょう。
コードと視覚化
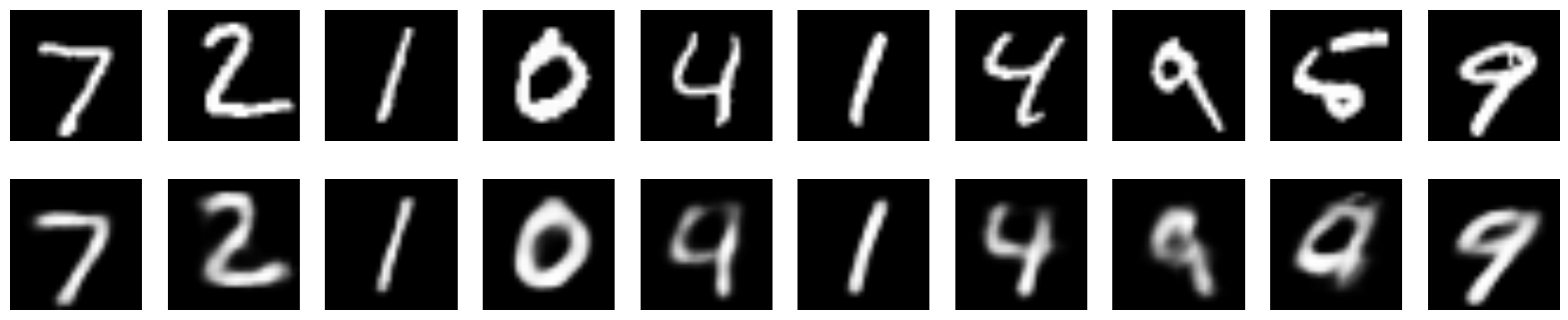
s_encoder, s_decoder, s_autoencoder = create_deep_sparse_ae(0.00001) s_autoencoder.compile(optimizer=Adam(0.0003), loss='binary_crossentropy')
s_autoencoder.fit(x_train, x_train, epochs=200, batch_size=256, shuffle=True, validation_data=(x_test, x_test))
imgs = x_test[:n] decoded_imgs = s_autoencoder.predict(imgs, batch_size=n) plot_digits(imgs, decoded_imgs)
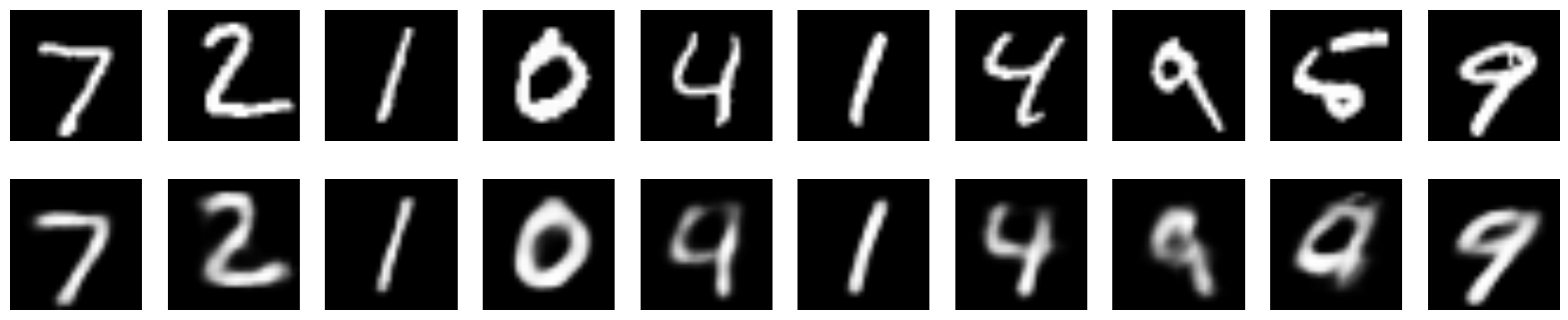
codes = s_encoder.predict(x_test) snt.jointplot(codes[:,1], codes[:,3])
そして 依然として互いに依存していますが、現在は少なくとも0を中心に分布しており、ほぼ正常です。
隠された空間を制御して、そこから画像をインテリジェントに生成できるようにする方法について-変分オートエンコーダー（VAE）の次の部分で 。
役立つリンクと文献
この投稿は、 Deep Learning Bookの Auto Encoders （特にautoencoders subheadingを使用したLearning maifolds ）に関する章に基づいています。