👼🏾 🤚🏻 🤸🏻 8DのZオーダー 📈 🛀🏼 ☹️

自己相似スイープ曲線に基づくインデックスは、空間データ検索の整理だけでなく適切です。それらは、整数格子上に置かれた異種データに対して機能します。

カットの下で、 Zカーブを使用してOLAPキューブに注目して8次元インデックスを実装する可能性をテストします。

前のシリーズの要約。

以前（1、2、3、4、5）、Z曲線に基づくインデックスが空間検索の編成に非常に適していることが示されました。（バッファキャッシュに制限がない場合）速度は従来使用されているRツリーに非常に近いですが、著しくコンパクトであり、ビルドが高速で、ランダムデータを恐れず、検索時に読み取りが少なくなります。

恐怖

技術的には、このようなインデックスを実装するのに複雑なことはありません;必要なのは、8次元キーの処理を行うことだけでした。 Dimension 8は技術的な理由から選択されました。7次元のインデックスが必要な場合、座標の1つにゼロを追加しても安全です。速度はほとんど変わりませんが、キーが長くなります。必要に応じて、16次元のキーなど、長くすることを妨げるものはありません。

どんな落とし穴が私たちに期待できるか、そしてそれに対して何をすべきかを事前に考える価値があります。

擬似ランダムデータで実験します。 しかし、実際のデータには特定のタスクに大きく依存する内部依存関係があり、予測することは困難です。はい、シミュレーションとして、実際には疑似ランダムデータは6次元であり、2つの列を単純に複製します。

一般に、この問題は、ページ分割/マージヒューリスティックを持つ多次元Rツリーにとって十分に基本的なものです。データの依存関係がヒューリスティックに適合しない場合、逆効果的に動作し始める可能性があります。これは、構築/作業の時間とインデックスのサイズに影響します。

インデックスが構築される通常のBツリーでは、この問題はそれほどひどくはありません。ツリー自体がバランスを維持しています。
実際には、異なる次元には異なるスケールがあり、最大範囲は1つの次元で平坦化し、別の次元で拡張できます。 はい、もちろんですが、これも多次元Rツリーを構築する際に非常に重要であり、Bツリーの場合はそれほど重要ではありません。
精度はどうですか？ 現在の実装では、値のエンコードに最大31ビットが許可されています。 データ（浮動小数点）が自然な方法で取得される場合、20ビットでエンコードするのに十分です。もちろん、32ビットADCがありますが、これはよりエキゾチックです。 doubleに64ビットが含まれていることは明らかですが、損失のない（または損失が最小の）ほとんどのデータを31ビットのグレーティングに置くことができます。そうでない場合、データは処理されました。たとえば、データは平均化されました。

必要に応じて、説明されているインデックスの解像度を上げることができます。これにより、キーの膨張とパフォーマンスの低下が生じます。ただし、ページに複数のキーが配置されている限り、Bツリーとして整理できます。

一方、精度のわずかな低下は、私たちの場合の基本ではありません。結局のところ、各次元の間隔を見ています。正しい結果を得るには、余裕を持って間隔を取り、不要なポストフィルタリングを削除するだけで十分です。
データは本質的に階層的である場合があります。 たとえば、数値はセンサーをエンコードしますが、センサーはグループ化され、グループが階層を形成します。 そして、この階層のブランチ全体で選択を行いたいです。 この問題は、ツリーノードを直接順番に走査して番号を付けることで解決されます。次に、ツリーの各ノードには、独自の識別子から最後の子孫の識別子までの値の間隔があります。

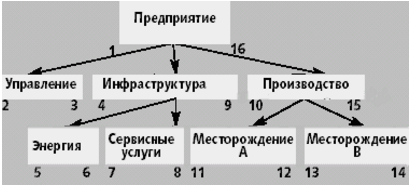
また、間隔は検索に必要なものです。
多次元の長方形は表面が発達しており、Z曲線のコーディングは非常に非効率的です。 そのような恐れがあり、同時に確認します。

ベンチマーク

次の表は、いくつかの種類のクエリの結果をまとめたものです（以下で説明）。

データ-側面[0 ... 1 000 000]を持つ8次元立方体に均等に分布する100 000 000のランダムポイント。

測定（以前と同様）は、2つのコアと4 GBのRAMを備えた仮想マシンで実行されたため、時間は絶対値ではありませんが、読み取りページ数を信頼できます。

ホットサーバーと仮想マシンでの2回目の実行で時間が表示されます。読み取られたバッファーの数は、新しく生成されたサーバー上にあります。

詳細

ここにコミットがあります：（SHA-1：36dd ... 76c7）

gawk -f gendata.awk〉 data.csv

 BEGIN {
   for（i = 0; i <100000000; i ++）
   {
     x = int（1000000 * rand（））;
     y = int（1000000 * rand（））;
     z = int（1000000 * rand（））;
     a = int（1000000 * rand（））;
     b = int（1000000 * rand（））;
     c = int（1000000 * rand（））;
     print "{" x "、" y "、" z "、" a "、" b "、" c "、" a "、" b "}";
   }
 }

「a」と「b」が2回出会うことに注意してください。縮退したデータがあり、実際の次元は6です。

create table test_points_8d (p integer[8]);
COPY test_points_8d from '/home/.../postgresql/contrib/zcurve/data.csv';

10分

\ dt +

スキーマ| 名前| タイプ| オーナー| サイズ| 説明 
 ------- + ---------------- + ------- + ---------- + ------ --- + -------------
公開|  test_points_8d | テーブル| ポストグレス|  8056 MB |

create index zcurve_test_points_8d on test_points_8d (zcurve_num_from_8coords (p[1], p[2], p[3], p[4], p[5], p[6], p[7], p[8]));

15分

\ di +

スキーマ| 名前| タイプ| オーナー| テーブル| サイズ| 
 -------- + ----------------------- + ------- + --------- -+ --------------- + ------- + ---
 公開|  zcurve_test_points_8d | インデックス| ポストグレス|  test_points_8d |  4743 MB

確認リクエスト

 select c, t_row from (select c, (select p from test_points_8d t where c = t.ctid) t_row from zcurve_8d_lookup_tidonly('zcurve_test_points_8d', 237000,291000,845000,152000,585000,193000,152000,585000, 247000,301000,855000,162000,595000,203000,162000,595000) as c) x;

返す

c | t_row 
      

        
        
        
      

     ------+----------------------------------------------------------- 
      

        
        
        
      

     (0,1) | {237787,291065,845813,152208,585537,193475,152208,585537}

必要に応じて

リクエストタイプ	NPoints	Nreq	時間（ミリ秒）	読みます	共有ヒット
10,000のすべて	1.1e-4	100,000	.46	2.0175	15.3919
すべて100,000	73.9	10,000	47	57.3063	1604.18
3X100,000 + 5x10,000	0.0837	10,000	.9	8.7637	73.8852
2X100,000 + 6x10,000	0.0096	10,000	.66	5.1771	40.9089
1全体+ 1X100,000 + 6X10,000	0.0978	10,000	1.5	24.2122	199.33
2全体+ 6X10,000	0.9663	10,000	95	115.202	1050.8

どこで

要求タイプは次のいずれかです

共通エクステントのサイドは1,000,000で、リクエストはサイドが10,000のキューブの形式であり、リクエストの開始は共通エクステント内で均等に分散されます。要求側は最大の1E-2です。なぜなら 6つの独立したパラメーターがあり、合計ボリュームの1E-12を取得します。ポイントの数は1E8です。これは、そのような範囲でポイントを見つける理論的な確率が約1E-4であることを意味します。
すべて100,000。要求範囲は、100,000辺のキューブであり、これは1e-1です。なぜなら 6つの独立したパラメーターがあり、ボリュームの1e-6を取得します。ポイント数は1e8です。これは、そのようなリクエストの平均ポイント数が100であることを意味します。一方、1つの座標で範囲から抜け出す確率は10％で、6〜53％（0.9 ** 6）のいずれかです。確率は0.735（0.95 ** 6）であり、得られた値と一致しています
3X100,000 + 5X10,000。リクエストは5つのディメンションによってフラット化されます
2100000 +610,000。リクエストは6次元でフラット化されます
全体で1 + 1X100,000 + 6X10,000。クエリは6次元でフラット化され、1つの次元は全体で取得され、1つは100,000です。値の1つが不明である場合、状況をシミュレートします。
全体として2 +6X10000。2つの値が全体として使用され、未知の状況を悪化させます。

NPoints-クエリで見つかった平均ポイント数

Nreq-クエリシリーズサイズ

時間（ミリ秒） -平均クエリ実行時間

読み取り -要求ごとの読み取りの平均数

共有ヒット -バッファキャッシュ内のヒット数

結論

予想どおり、要求の境界の領域は、要求のコストに重要な役割を果たします。実際、境界線が大きいほど、横断するページ数が大きくなる可能性があり、読む必要があるほど、キャッシュ効率が低下します...

ただし、キュービッククエリの場合、クエリのコストは許容範囲内です。実際、100,000の辺を持つキューブの場合、平均57ページが出力の74行で読み取られます。これらの74行を読むには、おそらくさらに74ページを読む必要があります。

さらに、このデータは均一に分散されたデータで取得され、クラスター化されたデータで同じ出力電力を取得するために、要求サイズと読み取りページ数がはるかに小さくなることが予想されます。

面白いですね。

PS：タイトル画像は八角形-8次元の立方体を示しています

PPS： Andrei Borodin（Oktonik、Ekb）に感謝します。トピックのヒントについて

8DのZオーダー

前のシリーズの要約。

恐怖

ベンチマーク

結論

More articles: