標準のC ++言語ライブラリは非常に優れています。 長年にわたり、標準アルゴリズムは単純なプラスを忠実に果たします!
しかし、業界全体が活況を呈しており、C ++がそれに伴います。 長い間、人々は標準的なアルゴリズムがどれほど優れていても、大きな欠点があることを理解し始めました:ゼロの構成可能性。 言い換えれば、いくつかの変換、フィルタリング、畳み込みなどのアルゴリズムをチェーンに組み合わせることは、追加の困難なく不可能です。 など
この問題を解決するためのいくつかのオプションがあります。 それらの1つ- 怠zyな計算と範囲 -は既に標準ライブラリに向かっています。
ただし、古き良きアルゴリズムを相殺するのは時期尚早です。
この記事では、アルゴリズムの構成可能性の問題に対する完全な解決策ではありませんが、古い標準アルゴリズムでの作業を非常に単純化することができ、C ++言語標準の将来のバージョンで作業するのに間違いなく役立つトリックの1つを検討したいと思います。
内容
機能オブジェクト技術
ポイントに直接進む前に、現在の標準ライブラリではまだあまり広く表現されていないが、少なくとも遅延計算が命令される部分では、STL2では非常に一般的であると思われるテクニックに触れたいおよび範囲。
経験豊富な方は、この部分を安全にスキップできます。
あなたはまだここにいますか 次に、コンテナのセットがあり、難しいタスクがあることを想像してください。これらすべてのコンテナの寸法を別のコンテナに記録することです。
コンテナのサイズを返す関数を作成します。
template <typename Container> constexpr decltype(auto) size (Container & container) { return container.size(); }
さて、標準std::transform
アルゴリズムを呼び出すことを妨げるものは何もありません。
std::vector<std::vector<int>> containers{...}; std::vector<std::size_t> sizes; std::transform(containers.begin(), containers.end(), std::back_inserter(sizes), size);
しかし、そこにあった:
// : // // couldn't deduce template parameter '_UnaryOperation' // std::transform(containers.begin(), containers.end(), std::back_inserter(sizes), size); // ^~~~
size
は定型的な機能です。 テンプレート関数は、明示的に(この場合はsize<std::vector<int>>
)、または呼び出し時に指定されます。 ただし、単にsize
記述するだけでは、コンパイラはこの関数がどの引数で呼び出されるかを理解できません。
size
関数としてではなく、 関数オブジェクトとして宣言すると、この問題を回避できます 。
struct size_fn { template <typename Container> constexpr decltype(auto) operator () (Container & container) { return container.size(); } }; constexpr auto size = size_fn{};
これで、コンパイルエラーはなくなりました。
std::transform(containers.begin(), containers.end(), std::back_inserter(sizes), size);
もちろん、賢明で賢明な人は、機能オブジェクトには機能に比べて特定の欠点があると言うでしょう。 しかし、今はこれに焦点を合わせません。
シンプルな構成
そのため、この手法は習得されています。より複雑な生活例を考えてみましょう。
連想配列からすべての関連する値を取得する必要があると想像してください。 これを行うには、既知のstd::transform
アルゴリズムを使用できます。
std::map<std::string, double> m{...}; std::vector<double> r; std::transform(m.begin(), m.end(), std::back_inserter(r), [] (const auto & p) {return p.second;});
これまでのところ、すべてが非常に簡単です。 短くて明確なラムダ関数、すべてが順調です。 しかし、表示ロジックがより複雑になると、状況は急激に悪化します。
たとえば、ペアの2番目の要素だけでなく、その平方根を計算し、結果を最も近い整数に丸める必要があります。 ラムダが長すぎるため、フォーマットする必要があります:
std::transform(m.begin(), m.end(), std::back_inserter(r), [] (const auto & p) { return std::lround(std::sqrt(p.second)); });
一方、私たちの意図はより短く、より明確に表現できます。
std::transform(m.begin(), m.end(), std::back_inserter(r), get<1> | sqrt | lround);
エントリget<1> | sqrt | lround
注目してくださいget<1> | sqrt | lround
get<1> | sqrt | lround
get<1> | sqrt | lround
。 この構文は次のように理解する必要があります。インデックス1のタプル要素を取得し、そこから平方根を取得して、最も近い整数に丸めます。 まさに必要なもの。
概略的には、これは次のように表すことができます。
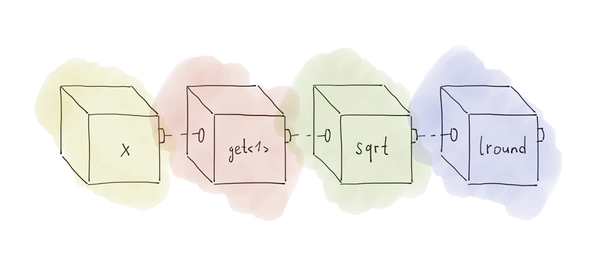
get
関数オブジェクトは、次のように実装できます。
template <std::size_t Index> struct get_fn { template <typename Tuple> constexpr decltype(auto) operator () (Tuple && t) const { using std::get; return get<Index>(std::forward<Tuple>(t)); } }; template <std::size_t Index> constexpr auto get = get_fn<Index>{};
機能オブジェクトsqrt
とlround
を、関心のあるすべての人への演習として実装することlround
提案します。
合成メカニズム自体は、対応する機能オブジェクトを通じて実装されます。
template <typename L, typename R> struct compose_fn { template <typename ... Ts> constexpr decltype(auto) operator () (Ts && ... ts) const & { return l(r(std::forward<Ts>(ts)...)); } template <typename ... Ts> constexpr decltype(auto) operator () (Ts && ... ts) & { return l(r(std::forward<Ts>(ts)...)); } template <typename ... Ts> constexpr decltype(auto) operator () (Ts && ... ts) && { return std::move(l)(std::move(r)(std::forward<Ts>(ts)...)); } L l; R r; }; template <typename L, typename R> constexpr auto compose (L && l, R && r) -> compose_fn<std::decay_t<L>, std::decay_t<R>> { return {std::forward<L>(l), std::forward<R>(r)}; } template <typename ... Ts, typename R> constexpr auto operator | (compose_fn<Ts...> l, R && r) { return compose(std::forward<R>(r), std::move(l)); }
この実装では、数学の慣習であるcompose
に、 compose
関数は右から左に合成を適用compose
ことに注意することが重要です。 つまり、 compose(f, g)(x)
f(g(x))
compose(f, g)(x)
同等です。
オペレーターは構成の順序を変更します。 つまり、 (f | g)(x)
g(f(x))
(f | g)(x)
同等です。
これは、 Boost Range Adapters 、 range-v3などのソリューションやコンソールパイプラインに精通しているプログラマーを誤解させないために行われます。
マルチポジション構成
これまでのところ、すべてが簡単で明確でした。 しかし、私たちはそこで止まりません。
ペアの配列をソートしたいとしましょう:
std::vector<std::pair<int, type_with_no_ordering>> v{...};
順序関係はペアの2番目の要素(名前から明らか)には指定されていないため、比較することは意味がありません;さらに、そのような比較は単にコンパイルされません。 したがって、次のようにソートを記述します。
std::sort(v.begin(), v.end(), [] (const auto & l, const auto & r) {return l.first < r.first;});
少し長く見えます。 あなたは美しさのためにそれをフォーマットすることができます。
std::sort(v.begin(), v.end(), [] (const auto & l, const auto & r) { return l.first < r.first; });
私の意見では、これは読書には便利ですが、それでもかなり冗長です。
この式は単純化できますか? 言葉でやりたいことを表現する擬似コードを書きましょう:
std::sort(v.begin(), v.end(), ___);
必要なアクション(最初の要素の比較)は、各ペアから最初の要素を取得することと実際の比較という2つの論理段階に分けることができます。
最初の要素を取得するには、既存のget
基づいて機能オブジェクトを作成します。
constexpr auto first = get<0>;
実際の比較のために、SBSにはすでに適切なツールstd::less
ます。
しかし、これらの機能をどのように組み合わせるのでしょうか? 問題を明確に説明しようとします。
std::sort
アルゴリズムstd::sort
は、2つのオブジェクトが入力されることを想定しています。
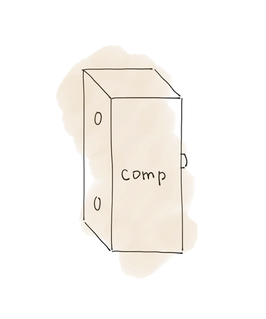
そして、 std::less
がこの条件を満たす。
同時に、 first
は1箇所の関数です。 引数は1つだけです。 適合しない:
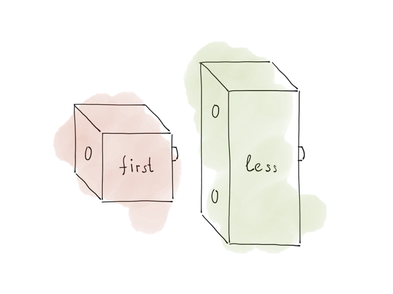
だからfirst | std::less{}
書くことはできませんfirst | std::less{}
first | std::less{}
同時に、取得したい結果は次のようになります。
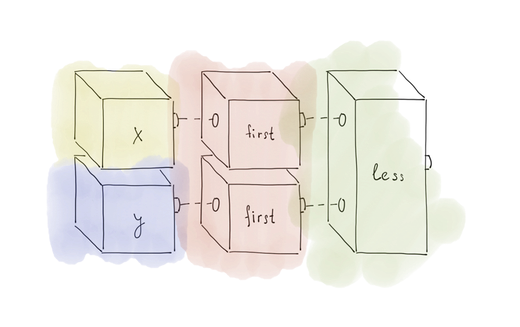
つまり、このブロック全体をstd::less
関数で構成する必要があります。
思考をコードに変換する場合、次のレコードを取得します。
std::sort(v.begin(), v.end(), each(first) | std::less<>{});
しかし、 each(first)
エントリによって生成された関数は、入力std::less
に送信するために、2つの値を受け入れるだけでなく、同時に2つの値を返す必要があることがstd::less
ます。 また、C ++では、関数は複数の値を返すことができません!
ただし、解決策があります。 機能オブジェクトeach
特別な構成スキームを実装する必要があります。
機能オブジェクトはeach
簡単です。
template <typename UnaryFunction> struct each_fn { UnaryFunction f; }; template <typename UnaryFunction> constexpr auto each (UnaryFunction && f) -> each_fn<std::decay_t<UnaryFunction>> { return {std::forward<UnaryFunction>(f)}; }
これは完全に機能するオブジェクトではありません。 むしろ、構成時に、コンテナ内に格納されている関数の構成を通常とは異なる方法で実行する必要があることを構成メカニズムに通知する特別なコンテナタグです。
そして、ここに合成のメカニズム自体があります:
template <typename L, typename R> struct each_compose_fn { template <typename ... Ts> constexpr decltype(auto) operator () (Ts && ... ts) const & { return l(r(std::forward<Ts>(ts))...); } template <typename ... Ts> constexpr decltype(auto) operator () (Ts && ... ts) & { return l(r(std::forward<Ts>(ts))...); } template <typename ... Ts> constexpr decltype(auto) operator () (Ts && ... ts) && { return std::move(l)(r(std::forward<Ts>(ts))...); } L l; R r; }; template <typename UnaryFunction1, typename UnaryFunction2> constexpr auto compose (each_fn<UnaryFunction1> l, each_fn<UnaryFunction2> r) -> each_fn<decltype(compose(lf, rf))> { return {compose(std::move(lf), std::move(rf))}; } template <typename L, typename UnaryFunction> constexpr auto compose (L && l, each_fn<UnaryFunction> r) -> each_compose_fn<std::decay_t<L>, UnaryFunction> { return {std::forward<L>(l), std::move(rf)}; } template <typename UnaryFunction, typename R> constexpr auto operator | (each_fn<UnaryFunction> l, R && r) { return compose(std::forward<R>(r), std::move(l)); }
通常の構成との主な違いは、引数リストの拡張です。
compose
関数では、展開は次のように行われます: l(r(args...))
、およびeach_compose
それ以外の場合: l(r(args)...)
つまり、最初のケースでは、単一の場所の関数が複数の場所の関数の結果に適用され、2番目の場合では、複数の場所の関数は単一の場所の関数を各入力パラメーターに適用した結果に適用されます。
これで、単一の場所の関数で複数の場所の関数を構成できます。
std::sort(v.begin(), v.end(), each(first) | std::less<>{}); std::lower_bound(v.begin(), v.end(), x, each(second) | std::greater<>{}); // ..
これは勝利です。
追加
多くの人は、各関数、オブジェクトの各プロパティなどに実装するには高すぎることに気付くでしょう。 個別の機能オブジェクト。 そして、これに反対することはできません。 たとえば、上の例の1 lround
、 lround
関数とsqrt
関数に新しい関数オブジェクトを実装せず、既存のライブラリ関数を使用する方が便利です。
この問題には不完全ですが、有効な解決策があります-ドラムロール-マクロ。
たとえば、クラスのメンバー関数を呼び出すには、次のようにマクロを実装できます。
#define MEM_FN(f)\ [] (auto && x, auto && ... args)\ -> decltype(auto)\ {\ return std::forward<decltype(x)>(x).f(std::forward<decltype(args)>(args)...);\ }
次のように使用されます。
std::vector<std::vector<int>> containers{...}; std::none_of(containers.begin(), containers.end(), MEM_FN(empty));
同様のマクロを実装して、無料の関数を呼び出すことができます。
#define FN(f)\ [] (auto && ... args)\ -> decltype(auto)\ {\ return f(std::forward<decltype(args)>(args)...);\ }
クラスメンバーにアクセスする場合でも:
#define MEMBER(m)\ [] (auto && x)\ -> decltype(auto)\ {\ /* , */\ /* */\ return (std::forward<decltype(x)>(x).m);\ } struct Class { int x; }; std::vector<Class> v{...}; std::remove_if(v.begin(), v.end(), MEMBER(x) | equal_to(5));
多くの新しいエンティティを導入しないように、コードはいくつかの場所で簡素化されています。
おわりに
これは何のためですか? なぜラムダを使用できないのですか?
lyabdyを使用することは可能であり、必要です。 しかし、残念ながら、ラムダは多くの場合重複コードを生成します。 ラムダが互いに完全に繰り返されることがあります。 いくつかのラムダがかなり異なることがありますが、分解はそれに適していません。
この記事で説明するアプローチにより、「キューブ」から単純なラムダを組み立てることができ、手書きコードの量が減り、その結果、別のラムダを書くときにミスをする可能性が減ります。
このアプローチは独立して機能しますが、主にアルゴリズムと範囲の作業を簡素化することを目的としています。