オブジェクトを使用した単純なPIDコントローラーモデルの検索
ネットワーク上の多数の出版物は、PIDコントローラーの動作のモデリングに専念しています。 Matlab Simulinkを使用したPIDコントローラーモデルの設計のリーダー[1,2](yandexで1億3,400万リンク)。 モデルを作成するプロセスは、単調です。 より多くの新しいブロックがモデルに転送されています。 手動マニピュレーターの1つの動きとPIDコントローラーがあり、もう1つはオブジェクトの伝達関数です。 ブロックを接続し、パラメーターを調整し、計算機を準備します。 はい、多くの機会がありますが、どういうわけかすべてが人工的すぎます。 そして、微分方程式、それらの解の方法、および長い間私たちをだましてきたその計算法が存在する理由はすでに完全に理解不能になっています。 MathcadでのPIDの実装を探しています。ここでは、同じyandex内のリンクが少なく、わずか8100万であり、より多くの数学と数式があります。 Mathcad 14に同梱されているPIDの例を考えてください。

オブジェクトとして、振動リンク。 多くの賢い説明がありますが、最終的にはlaplaceとinvlaplaceの2つの演算子があります。 一般的な伝達関数は、分子に2次演算子、分母に4次演算子を持ちます。 3つのPIDコンポーネントすべてが接続されているときにlaplaceおよびinvlaplace演算子が機能するように、伝達関数の分母の根も見つけます。これらの根は複素共役です。
現在、PythonでのPID実装を探しています。 静かに9700万件の結果を喜んでいたが、長くは続かなかった。 Python 2.7について、ESP32サンプルを使用したArduinoファームウェアに関してのみ。 しかし、これでさえPythonの誇りで心を満たしています。
検索に失望したので、私は自分のモデルを控えめな能力よりも最大限に自分で書くことにしました。
制御オブジェクトのブロック図
問題の説明は[3]から引用したもので、規制対象の構造の多様性に惹かれました。 途中でいくつかのエラーを修正しました。 そのため、最終微分方程式では、T2で正方形が失われ、a2のテーブルデータは近似結果に対応しませんでした。 さらに、彼は移行プロセスの状況を活性化するために、単一の無限インパルスの形で制御設備を導入しました。 PIDコントローラーが[3]のように見えるのは、どういうわけか自然ではありません。
次のブロック図を使用して規制システムを検討します。
- 振動リンク[4]は、2次微分方程式で記述されます。
- 表データによって決定される入力への出力の依存性を決定する線形静的リンク。 データは実験的に取得できます。 データ取得エラーのため、線形近似を適用する必要があります
。
- 2番目の線形静的リンク-入力の出力の依存性は、実験的に取得できる表形式のデータによって決定されます。データ取得のエラーのため、線形近似を適用する必要があります。
。
- 入力がブロック2,3からの信号の合計を受け取る線形ダイナミックリンク
リンクには伝達関数があり、これは1次の線形微分方程式で記述されます。
- 比例係数を使用して制御オブジェクトに調整する、既知の制御法則を備えたPIDコントローラー
一次関数、微分係数付き
一次導関数および積分係数
不定積分で。
単一の入力アクション1(t)は、1 / pとして演算子形式に変換されます。 得られた結果として、式1.4を演算子に変換します。
(5)の両側を区別します。このため、単に演算子pを乗算します。
式(2)、(3)を演算子形式に変換し、y(y1)を表します。
(6)に(7)を代入すると、次のようになります。
(8)を時間領域に渡します;このため、演算子形式を微分方程式で置き換えます。
PythonでPIDコントローラーの設定を決定する問題の解決策
規制対象の以下のパラメーターを設定します。
T1 = 7.0; T2 = 5.0; s = 0.4; k1 = 5.5; k2 = 5.5。 ユニット2、3の特性を概算するためのデータは、表にまとめられています。
レギュレーターなしでオブジェクトを残しましょう、これのために
プログラムコード
#!/usr/bin/python # -*- coding: utf-8 -*- import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt def mnkLIN(x,y,q): # a=round((len(x)*sum([x[i]*y[i] for i in range(0,len(x))])-sum(x)*sum(y))/(len(x)*sum([x[i]**2 for i in range(0,len(x))])-sum(x)**2),3) b=round((sum(y)-a*sum(x))/len(x) ,3) y1=[round(a*w+b ,3) for w in x] s=[round((y1[i]-y[i])**2,3) for i in range(0,len(x))] sko=round((sum(s)/(len(x)-1))**0.5,3) if q==1: plt.subplot(221) plt.plot(x, y, color='r', linewidth=2, marker='o', label=' a= %s'%str(a)) plt.plot(x, y1, color='g', linestyle=' ', marker='o', label=' =%s'%str(sko)) plt.legend(loc='best') plt.grid(True) else: plt.subplot(222) plt.plot(x, y, color='r', linewidth=2, marker='o', label=' a= %s'%str(a)) plt.plot(x, y1, color='g', linestyle=' ', marker='o', label=' =%s'%str(sko)) plt.legend(loc='best') plt.grid(True) return a T1=7.0;T2=5.0;s=0.4;k1=5.5;k2=5.5# . x=[0,1,2,3,4,5] y=[0,-11,-22,-33,-44,-55] a2=mnkLIN(x,y,1) x=[0,1,2,3,4,5] y=[0,17,34,51,68,85] a3=mnkLIN(x,y,2) #m1=0.5;m2=2.0;m3=0.3# . m1=0.0;m2=0.0;m3=0.0 a=a2+a3 A=round((s*T1*T2+T1**2)/(T1*T2**2),3) B=round((T2+s*T1+k1*k2*m2*a)/(T1*T2**2),3) C=round((1+k1*k2*m1*a)/(T1*T2**2),3) D=round(k1*k2*m3*a/(T1*T2**2),3) E=round(k1*k2*a/(T1*T2**2),3) def f(y, t):# . y1,y2,y3,y4 = y return [y2,y3,y4,-A*y4-B*y3-C*y2-D*y1+E] t = np.linspace(0,100,10000) y0 = [0,1,0,0]# w = odeint(f, y0, t) y1=w[:,0] # y2=w[:,1] # plt.subplot(223) plt.plot(t,y1,linewidth=1, label=' p- %s,d- %s,i- %s,'%(str(m1),str(m2),str(m3))) plt.ylabel("z") plt.xlabel("t") plt.legend(loc='best') plt.grid(True) plt.show()
ロボットプログラムの結果。
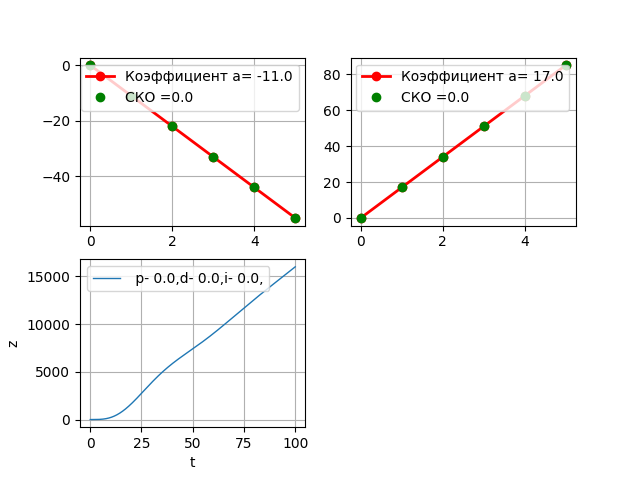
PIDコントローラーがないと、オブジェクトはスペースになりました。 PIDパラメーターの予備選択後、取得します。
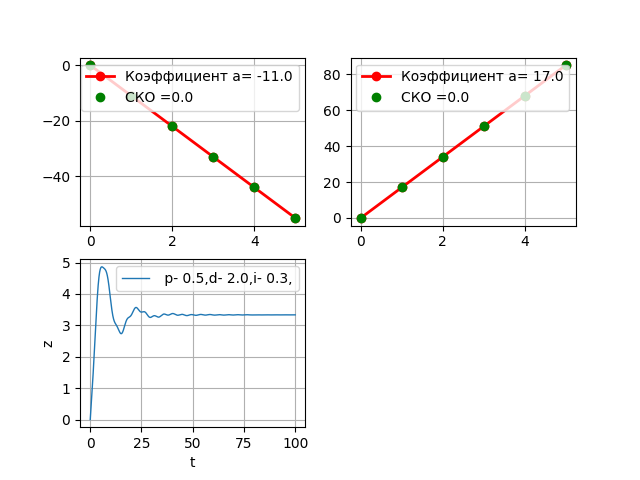
3番目のリンクの表形式データを変更し、a3を2回増やします。
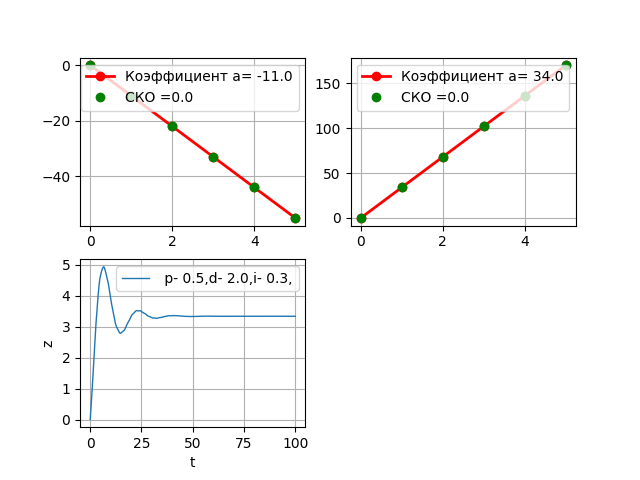
レギュレーターは安定しています。
Pythonで方程式(9)を解く関数を選択し、結果をMatcadのソリューションと比較する
scipyライブラリのodeint関数を使用しました。 統合する
def f(y, t):# . y1,y2,y3,y4 = y return [y2,y3,y4,-A*y4-B*y3-C*y2-D*y1+E] t = np. linspace(0,100,10000) y0 = [0,1,0,0]# w = odeint(f, y0, t) y1=w[:,0] # y2=w[:,1] #
式(9)を再構築して、左側に高次の導関数が存在し、右側に他のすべてが存在する場合、次のようになります。
これが関数def f(y、t)の構築方法です。 odeint関数には3つの必須引数があり、このodeint(func、y0、t [、args =()、...])のように見えます。
比較のために、指定された関数def f(y、t)で使用される変数A、B、C、D、Eの値を導出し、0.36 7.996 1.994 1.193 3.976を取得します。 Mathcad 14で微分方程式(9)を解くためのプログラムを作成し、遷移特性を構築します。
グラフと数値は完全に同一です。 したがって、Odesolve Mathcadおよびodeint Python関数は、記事で提示された問題に対して同じ数値解を提供します。
おわりに
開発のこの段階で、SciPyおよびNumPyライブラリを備えたPythonプログラミング言語は、動的および静的リンクを含む自動制御ループの数値モデリングに効果的に使用できます。