learnopengl。 レッスン1.9-カメラ

前のレッスンでは、ビューマトリックスと、それを使用してシーン内を移動する方法について説明しました（観察者の視点を少し移動しました）。 OpenGLにはカメラの概念はありませんが、シーン内のすべてのオブジェクトを観察者とは反対の方向に移動することでシミュレートし、それによって移動しているような錯覚を作成できます。

このチュートリアルでは、OpenGLでカメラを作成する方法について説明します。 FPS（ファーストパーソンシューター）のようなカメラについて説明します。FPSを使用すると、3次元のシーンを自由に移動できます。 さらに、キーボードとマウスの入力について説明し、最終的に独自のC ++カメラクラスを作成します。

カメラ/ビュースペース

カメラ/ビュースペースについて話すとき、カメラの視点からのすべての頂点のビューを意味します。このスペース内の位置は原点の基点です。ビューマトリックスは、カメラの位置と方向に対して測定されたワールド座標をビュー座標に変換します。 カメラの明確な数学的記述には、ワールド空間での位置、カメラが見ている方向、正しい方向を示すベクトル、および上方向を示すベクトルが必要です。 注意深い読者であれば、実際には、3つの垂直軸とカメラの位置を基準点とする座標系を作成しようとしていることに気付くかもしれません。

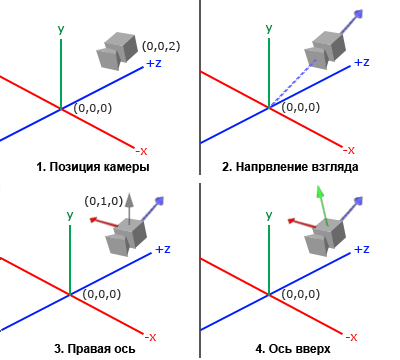
1.カメラの位置

カメラの位置を取得するのは簡単です。 カメラの位置は、ワールド空間でのカメラの座標を含むベクトルです。 前のレッスンで設置したのと同じ場所にカメラを配置します。

glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 3.0f);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Z軸の正の方向が画面の面をあなたの方へ通過することを忘れないでください。したがって、カメラを後方に移動させたい場合は、正のZ軸に沿って移動します。

2.カメラの方向

次に必要なベクトルはカメラの方向ベクトルです。 これまでのところ、カメラはシーンの基点（0,0,0）に向けられています。 2つのベクトルを互いに減算すると、元のベクトルの差であるベクトルが得られることを忘れていませんか？ 原点からカメラ位置ベクトルを引くと、カメラ方向ベクトルが得られます。 カメラはZ軸の負の方向に向かっていることを知っており、カメラ自体の正のZ軸に沿ったベクトルが必要です。 減算するときに引数の順序を変更すると、カメラのZ軸の正の方向を指すベクトルが得られます。

 glm::vec3 cameraTarget = glm::vec3(0.0f, 0.0f, 0.0f); glm::vec3 cameraDirection = glm::normalize(cameraPos - cameraTarget);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

「 方向ベクトル」という名前は、このベクトルが実際にカメラの方向と反対の方向を指しているため、完全に適切ではありません。

3.右軸

これなしではできないもう1つのベクトルは、 右を指し、カメラのX軸の正の方向を表すベクトルです。 このベクトルを計算するには、ちょっとしたトリックを行います。このために、まず上方向（ワールド空間内）を示すベクトルを設定します。 次に、ステップ2で計算したカメラの方向と上向きのベクトルをベクトルで乗算します。 ベクトル積の結果は元のベクトルに垂直なベクトルであるため、X軸の正の方向を指すベクトルが得られます（因子を交換すると、X軸の負の方向を指すベクトルが得られます）。

 glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f); glm::vec3 cameraRight = glm::normalize(glm::cross(up, cameraDirection));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

4.軸を上に

2つの軸XとZのベクトルができたので、カメラの軸Yの正の方向を指すベクトルを取得するのは非常に簡単です。右のベクトルとカメラの方向ベクトルのベクトル乗算を行います。

 glm::vec3 cameraUp = glm::cross(cameraDirection, cameraRight);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ベクトル積と小さなトリックの助けを借りて、カメラ/ビュースペースを定義するすべてのベクトルを計算することができました。 数学の読者にとってより洗練された線形代数のこのアルゴリズムは、Gram-Schmidtプロセスとして知られています。 これらのベクトルを使用して、 LookAtマトリックスを作成できます。これは、カメラの作成に非常に役立ちます。

Lookat

マトリックスの注目すべき特性の1つは、3つの垂直（または線形独立）軸を使用して座標空間を定義する場合、これらの軸のベクトルと追加の変位ベクトルから、任意のベクトルをこれに変換するマトリックスを形成できることです座標空間。 これはまさにLookAtマトリックスが行うことであり、カメラ/ビュースペース、つまり 3つの垂直軸とカメラ位置ベクトルを使用して、独自のLookAtマトリックスを作成できます。

$$

$$LookAt = \ begin {bmatrix} \ color {red} {R_x}＆\ color {red} {R_y}＆\ color {red} {R_z}＆0 \\ \ color {green} {U_x}＆\ color {緑} {U_y}＆\ color {green} {U_z}＆0 \\ \ color {blue} {D_x}＆\ color {blue} {D_y}＆\ color {blue} {D_z}＆0 \\ 0＆ 0＆0＆1 \ end {bmatrix} * \ begin {bmatrix} 1＆0＆0＆-{\ color {Purple} {P_x}} \\ 0＆1＆0＆-\ color {Purple} {P_y} \\ 0＆0＆1＆-\ color {Purple} {P_z} \\ 0＆0＆0＆1 \ end {bmatrix}$$

ここで、 Rは右ベクトル、 Uは上向きのベクトル、 Dはカメラの方向ベクトル、 Pはカメラの位置です。 最後にカメラの動きとは反対の方向にワールド座標をシフトするため、カメラの位置ベクトルが反転することに注意してください。 LookAtマトリックスをビューマトリックスとして使用すると、すべてのワールド座標を指定したスペースに効率的に変換できます。 LookAtマトリックスは、その名前が示すとおりに機能します。指定されたターゲットを見るビューマトリックスを作成します。

幸いなことに、GLMライブラリはこの作業をすべて行います。 カメラの位置、ターゲットの座標、上向きのワールド空間内のベクトル（正しいベクトルを計算するために使用した補助ベクトル）を指定するだけです。 これらのデータに基づいて、GLMは独立してLookAtマトリックスを作成し、次の形式のマトリックスとして使用できます。

 glm::mat4 view; view = glm::lookAt(glm::vec3(0.0f, 0.0f, 3.0f), glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(0.0f, 1.0f, 0.0f));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

glm :: LookAt関数には、カメラ位置、ターゲット座標、上向きベクトルのパラメーターが必要です。 この関数は、前のレッスンで使用したものと同じビュー行列を計算します。

ユーザー入力の問題を掘り下げる前に、いくつかの楽しみを持ち、カメラをシーンの周りで回転させましょう。 簡単にするために、カメラを常にポイント（0,0,0）に向けます。

カメラの位置を計算するために、小さな三角法を適用し、各フレームのX座標とZ座標を計算します。X座標とZ座標は、円形パス上にあるポイントになります。 各フレームのX座標とZ座標を再計算して、円のすべてのポイントを調べます。したがって、カメラはシーンの周りを回転します。 この円のサイズを半径の一定値として設定し、GLFWライブラリのglfwGetTime関数を使用して、ゲームループの各反復に対して次の形式の新しい行列を計算します。

 GLfloat radius = 10.0f; GLfloat camX = sin(glfwGetTime()) * radius; GLfloat camZ = cos(glfwGetTime()) * radius; glm::mat4 view; view = glm::lookAt(glm::vec3(camX, 0.0, camZ), glm::vec3(0.0, 0.0, 0.0), glm::vec3(0.0, 1.0, 0.0));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このコードを実行すると、次のようなものが表示されます。

さて、この小さなコードで、カメラはシーンを中心に回転します。 LookAtの仕組みを理解するために、半径と位置/方向のパラメーターを自由に試してください。 うまくいかない場合は、コードをソースコードと比較し、シェーダーを頂点シェーダーとフラグメントシェーダーのテキストと比較します。

散歩する

シーンの周りでカメラを回転させることは確かに楽しいですが、もっと面白いのは自分でそれを動かすことです！ まず、カメラの「インフラストラクチャ」を作成する必要があります。このため、プログラムの最初にいくつかの変数を定義しましょう。

 glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 3.0f); glm::vec3 cameraFront = glm::vec3(0.0f, 0.0f, -1.0f); glm::vec3 cameraUp = glm::vec3(0.0f, 1.0f, 0.0f);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

LookAt関数の呼び出しは次のようになります。

 view = glm::lookAt(cameraPos, cameraPos + cameraFront, cameraUp);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

まず、カメラの位置がcameraPos変数に格納されている位置にカメラを設定します。 カメラの方向は、現在の位置+ cameraFrontベクトルとして計算されます。これは、先ほど発表し初期化したものです。 これにより、カメラが動いていても、常にターゲットの方向を見ることができます。 キーストロークでcameraPosベクトルを変更して、これらの変数を少し試してみましょう。

レッスン1.3では、 GLFWからキーボード入力を受信するために必要なkey_callbackコールバック関数を作成しました。 次に 、特定のボタンを押す際にいくつかの新しいチェックを追加しましょう。

 void key_callback(GLFWwindow* window, int key, int scancode, int action, int mode) { ... GLfloat cameraSpeed = 0.05f; if(key == GLFW_KEY_W) cameraPos += cameraSpeed * cameraFront; if(key == GLFW_KEY_S) cameraPos -= cameraSpeed * cameraFront; if(key == GLFW_KEY_A) cameraPos -= glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed; if(key == GLFW_KEY_D) cameraPos += glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

WASDキーのいずれかを押すたびに、カメラの位置は新しい座標に従って更新されます。 前方または後方に移動する場合は、カメラ位置ベクトルに方向ベクトルを追加または減算します。 横方向に移動するとき、ベクトル積を使用して、右に向けられたベクトルを見つけ、それに沿って移動します。 横方向のカメラシフトにより、ゲーマーになじみのあるストラフェ効果を作成します。

結果の右ベクトルを正規化することに注意してください。 これを行わなかった場合、 cameraFrontの値に応じて、ベクトル積の結果は異なる長さのベクトルになる可能性があります。 適切なベクトルを正規化しないと、カメラの速度は一定ではなく、カメラの方向が変わると加速または減速します。

このコードでkey_callback関数を補完すると 、シーンを前後に移動したり、前後に移動したりできます。

このシンプルなカメラ制御システムを楽しんでいると、おそらく2方向に同時に移動することはできないことに気づいたでしょう（斜めに移動します）、キーの1つを保持すると、最初に1回動作し、その後少し遅れて開始します連続的な動き。 これは、ほとんどの入力システムに、対応するハンドラーを呼び出すキーストロークを一度に1つしか処理できないイベント駆動型アーキテクチャ（EDA）があるためです。 これは多くのGUIシステムでうまく機能しますが、スムーズなカメラの動きにはあまり適していません。 この問題を解決するためのちょっとしたトリックを紹介します。

秘Theは、 key_callbackコールバック関数でどのキーが押されたか、 離されたかを追跡することです。 次に、ゲームループでこれらの値を考慮し、アクティブなキーを確認し、その状態に基づいて、 cameraPos変数の値を適宜変更します。 したがって、ハンドラー関数では、どのキーが押されたか、または離されたかに関する情報を保存するだけで、ゲームループで既にそれらの状態に応答します。 まず、キーの押された状態または離された状態を表すブール変数の配列を作成しましょう。

 bool keys[1024];
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

その後、 key_callback関数で、押されたキーをtrueに 、リリースされたキーをfalseに設定する必要があります。

 if(action == GLFW_PRESS) keys[key] = true; else if(action == GLFW_RELEASE) keys[key] = false;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、 do_movementを呼び出す新しい関数を作成します。この関数では、押されたキーの状態に応じてカメラ座標を更新します。

 void do_movement() { // Camera controls GLfloat cameraSpeed = 0.01f; if(keys[GLFW_KEY_W]) cameraPos += cameraSpeed * cameraFront; if(keys[GLFW_KEY_S]) cameraPos -= cameraSpeed * cameraFront; if(keys[GLFW_KEY_A]) cameraPos -= glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed; if(keys[GLFW_KEY_D]) cameraPos += glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

前のセクションのコードがdo_movement関数に移植されました。 キー識別子のGLFW列挙は単なる整数であるため、それらを使用して配列のインデックスを作成できます。

最後に、ゲームループの本体に新しい関数呼び出しを追加する必要があります。

 while(!glfwWindowShouldClose(window)) { //        glfwPollEvents(); do_movement(); //  ... }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、2つの方向に同時に移動できるようになり、キーを押した直後に連続的な移動が開始されます。 何かにこだわっている場合は、コードをソースコードと自由に比較してください。

移動速度

現在、カメラを移動するときの移動速度の定数値を使用します。 理論的にはこれは普通のように見えますが、実際にはユーザーによって計算能力が大きく異なり、その結果、一部のコンピューターでは同時に他のコンピューターよりもはるかに多くのフレームが描画されます。 また、あるユーザーが別のユーザーよりも多くのフレームを描画すると、 do_movement関数がより頻繁に呼び出されます。

その結果、コンピューターの構成に応じて、一部のユーザーはシーン内を非常にすばやく移動し、他のユーザーは非常に遅くなります。 しかし、プログラムを配布する場合は、おそらくどのハードウェアでも同じように動作させたいでしょう。

グラフィックアプリケーションとゲームは通常、特別な変数deltaTimeを使用します。 この変数には、表示された最後のフレームをレンダリングするのにかかった時間が格納されます。 そして、ゲームで指定されたすべての速度にこのdeltaTime値が乗算されます。 その結果、フレーム出力に多くの時間がかかり、 deltaTime値が大きい場合、この変数を掛けた速度が大きくなり、全体的なパフォーマンスのバランスが取れます。 このアプローチを使用すると、コンピューターの電力はプログラムの動作に影響を与えなくなります。コンピューターが遅いか非常に速いかは関係ありません。カメラの速度はいずれにしても調整され、すべてのユーザーが同じ結果になります。

deltaTime値を計算するには、2つのグローバル変数が必要です。

 GLfloat deltaTime = 0.0f; // ,       GLfloat lastFrame = 0.0f; //    
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、各フレームで、後で使用するために新しいdeltaTime値を計算します。

 GLfloat currentFrame = glfwGetTime(); deltaTime = currentFrame - lastFrame; lastFrame = currentFrame;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

deltaTimeができたので、速度を計算するときにその値を考慮することができます。

 void do_movement() { GLfloat cameraSpeed = 5.0f * deltaTime; ... }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

前のセクションのコードと一緒に、シーン内でカメラを移動するためのよりスムーズで一貫したシステムを取得する必要があります。

そして今、どのシステムでも同じ速度で動くカメラがあります。 何かが失敗した場合は、 ソースコードを再度確認してください。 後で、 deltaTime値が、速度と動きに関連するコードで頻繁に表示されることを確認します。

ご覧ください

キーボードだけを使用して移動することは、あまり面白くないです。 さらに、方向転換する能力の欠如により、私たちの動きはかなり制約されます。 それはマウスが便利になるところです！

シーンを自由に検査するには、マウス入力によってガイドされるカメラcameraFrontの方向ベクトルを変更する必要があります。 ただし、マウスの回転に基づいて方向ベクトルを変更すると、特定の困難が生じ、三角法に関するある程度の知識が必要になります。 三角法がわからなくても心配する必要はありません。 ソースコードがあるセクションに移動してプログラムに貼り付けるだけで、詳細を知りたい場合はいつでも戻ることができます。

オイラー角

オイラー角は、1700年代頃にレナードオイラーによって記述された3つの量であり、3次元空間での任意の回転を表すことができます。 オイラー角には、 ピッチ 、 ヨー 、 ロールの 3つがあります。 次の図に明確に示されています。

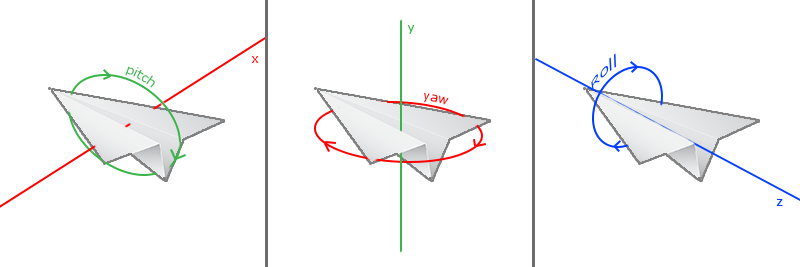
最初の画像でわかるように、 ピッチはチルトの上下の量を特徴付ける角度です。 2番目の画像は、左右の回転量であるヨーを示しています。 ロールは、縦軸に沿って回転を設定し、通常、さまざまなフライトシミュレータでよく使用されます。 各オイラー角は1つのスカラー量で定義され、3つすべての角度の組み合わせにより、3次元空間で任意の回転ベクトルを計算できます。

カメラ制御システムでは、ヨー角とピッチ角のみを使用するため、ここではロール値については説明しません。 ヨーとピッチを使用して、3Dカメラの方向ベクトルに変換できます。 ヨーとピッチを方向ベクトルに変換するプロセスには、少しの三角計算が必要です。 簡単な例から始めましょう：

斜辺の長さを1に設定すると、主な三角関係から（soh cah toa：Sine Opposite Hypotenuse、Cosine Adjacent Hypotenuse、Tangent Opposite Adjacent、つまり、正弦は斜辺に対する反対側の比であり、余弦は斜辺に対する隣接側の比です、接線は反対側と隣接側の比です）隣接する側の長さはcos X / h = cos X / 1 = cos Xであり、反対側の長さはsin Y / h = sin Y / 1 = sin Yであることが知られています これらの式は、与えられた角度のX軸とY軸上の斜辺の投影の長さを計算する機会を与えてくれます。 それらを使用して、カメラ方向ベクトルのコンポーネントを計算します。

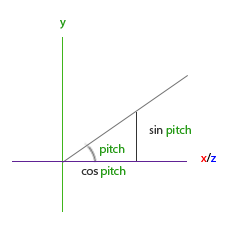
この三角形は、前の図の三角形に似ています.XZ平面上にあり、Y軸を見ると、最初の三角形に与えられた式に従って方向ベクトルのY成分の値を計算できます（方向を上下に設定）。 この図は、与えられたピッチ角sinΘに対するYの値を示しています。

 direction.y = sin(glm::radians(pitch)); // ,        
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここでは、Yの値のみを計算しました。次に、コンポーネントXとZを計算する必要があります。三角形の画像を見ると、値が等しいことがわかります。

 direction.x = cos(glm::radians(pitch)); direction.z = cos(glm::radians(pitch));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ヨー角の方向ベクトルの対応するコンポーネントを見つける方法を見てみましょう。

ピッチ角に対して作成された三角形の図のように、この図はcos（ヨー）の値に対するX成分の依存性と、sin（ヨー）のZ成分の依存性を示しています。 これらの値をピッチ角に対して計算された結果と組み合わせると、ピッチとヨーの2つの回転角で構築された最終的なカメラ方向ベクトルが得られます。

 direction.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw)); direction.y = sin(glm::radians(pitch)); direction.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これにより、ピッチ角とヨー角を3次元の方向ベクトルに変換するための式が得られます。これを使用して、カメラの向きを決めることができます。 おそらくすでに質問をされているでしょう：ヨー角とピッチ角をどのように取得するのですか？

マウス制御

ピッチ角とヨー角は、マウス（またはゲームコントローラ/ジョイスティック）の動きに応じて値が変化します。 マウスの横方向の動きはヨー角に影響し、前後の動きはピッチ角に影響します。 これは、最後のフレームのマウス座標を保存し、現在のフレームでそれらを新しい座標と比較して、マウスポインターが移動したピクセル数を計算するというものです。 このシフトが大きいほど、ピッチおよび/またはヨーの値が大きく変化し、それに応じてカメラがより大きな角度になります。

まず、GLFWライブラリに、カーソルをつかんでマウスポインターを非表示にするように指示します。 カーソルをキャプチャするとは、アプリケーションが入力フォーカスを受け取った後、カーソルがウィンドウ内に残ることを意味します（アプリケーションがフォーカスを失うか、作業を完了するまで）。 1つの簡単な設定呼び出しでこれを行うことができます。

 glfwSetInputMode(window, GLFW_CURSOR, GLFW_CURSOR_DISABLED);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この呼び出しの後、マウスをどこに移動しても、そのポインターは表示されず、ウィンドウの境界を越えることはできません。 これは、FPSなどのゲームでカメラを制御するのに最適です。

, , GLFW, . ( ), :

 void mouse_callback(GLFWwindow* window, double xpos, double ypos);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

xpos ypos . , GLFW mouse_callback , :

 glfwSetCursorPosCallback(window, mouse_callback);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

FPS, , :

1. .
2. .
3. / /

. - . , ( 800 600):

 GLfloat lastX = 400, lastY = 300;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

:

 GLfloat yaw = -90.0f; GLfloat pitch = 0.0f;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

, :

 GLfloat xoffset = xpos - lastX; GLfloat yoffset = lastY - ypos; //       Y-     lastX = xpos; lastY = ypos; GLfloat sensitivity = 0.05f; xoffset *= sensitivity; yoffset *= sensitivity;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

, sensitivity (). , ; .

pitch yaw :

 yaw += xoffset; pitch += yoffset;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

, ( ). , 89 ( 90 , 89), -89 . , . :

 if(pitch > 89.0f) pitch = 89.0f; if(pitch < -89.0f) pitch = -89.0f;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

, , . , , , .

, :

 glm::vec3 front; front.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw)); front.y = sin(glm::radians(pitch)); front.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw)); cameraFront = glm::normalize(front);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

, . cameraFront glm::lookAt , .

, , , . , mouse_callback xpos ypos . , , , . - bool , , xpos ypos ; , :

 if (firstMouse) //      true { lastX = xpos; lastY = ypos; firstMouse = false; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

:

 void mouse_callback(GLFWwindow* window, double xpos, double ypos) { if(firstMouse) { lastX = xpos; lastY = ypos; firstMouse = false; } GLfloat xoffset = xpos - lastX; GLfloat yoffset = lastY - ypos; lastX = xpos; lastY = ypos; GLfloat sensitivity = 0.05; xoffset *= sensitivity; yoffset *= sensitivity; yaw += xoffset; pitch += yoffset; if(pitch > 89.0f) pitch = 89.0f; if(pitch < -89.0f) pitch = -89.0f; glm::vec3 front; front.x = cos(glm::radians(yaw)) * cos(glm::radians(pitch)); front.y = sin(glm::radians(pitch)); front.z = sin(glm::radians(yaw)) * cos(glm::radians(pitch)); cameraFront = glm::normalize(front); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

! , 3D-! - , .

: , firstMouse , glfwSetCursorPos — lastX lastY glfwGetCursorPos .

. , fov . , , . . , , :

 void scroll_callback(GLFWwindow* window, double xoffset, double yoffset) { if(fov >= 1.0f && fov <= 45.0f) fov -= yoffset; if(fov <= 1.0f) fov = 1.0f; if(fov >= 45.0f) fov = 45.0f; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

yoffset , . scroll_callback , fov . fov 45.0f, 1.0f 45.0f.

, - fov , , :

 projection = glm::perspective(fov, (GLfloat)WIDTH/(GLfloat)HEIGHT, 0.1f, 100.0f);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

, , :

 glfwSetScrollCallback(window, scroll_callback);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

, , . , .

, - , .

: , , . . , .

Camera

. , , , , . , , ( ) , , .

, Shader, Camera . Camera . . , .

FPS- , , . , . , FPS- 90 , (0,1,0) , .

Camera .

演習

• , , FPS-, c , , XZ: .
• LookAt , , . glm::LookAt , : .