Clever Geek Handbook

Scilab Freefall

最近、HabréにScilabに関する記事がほとんどないことに驚いた。 一方、それはオープンでクロスプラットフォームのコンピューター数学のかなり強力なシステムであり、幅広い工学的および科学的問題をカバーしています。 多くの大学（UrFU、ITMOなど）では、学生の教育に使用されています。 最も差し迫った工学上の問題の1つは、微分方程式の解法です（以降-DE）。 この記事では、有名な成層圏ジャンプFelix Baumgartnerのモデリング例を使用して、Scilabを使用して通常のリモートコントロールシステムを解決する方法を示します。







バウムガルトナーフリーフォール






ご存知のように、 自由落下は、重力の作用下で、身体に作用する他の力が存在しないか無視できる場合、同様に変動する動きです。 日常生活では、空気抵抗と重力以外の力が身体の加速に影響を与えない場合、自由落下は地球の大気中の動きとも呼ばれます。 将来的に使用するのはこの拡張された理解です。







挑戦する



バウムガルトナーの飛行の本質的な特性を記述する微分方程式（DU）を作成し、Scilabを使用してそれらを解き、自由落下時間に対する距離と速度の依存性を明示的に取得します。







ソースデータ



なぜなら この記事の主な目的は、ScilabがODEを解決する方法を示すことであり、完全に正確なモデルを取得することではありません。実験データ（テレメトリ）、エラー、フィッティングの分析には特に関心がありません。 ただし、モデルの妥当性を検証するには、いくつかの値をとる必要があります。 だから：













出典： ウィキペディア 、 プレス 、 ビデオ







モデル-1（空気抵抗を除く）



まず、最も単純なモデルから始めましょう。このモデルでは、力は1つだけで、地球の重力です。 落下は厳密に垂直であり、原点はジャンプの開始点にあり、y軸は下を向いていると考えられます。













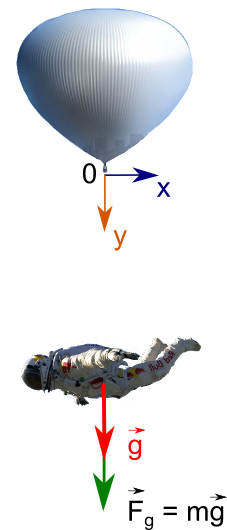
極値の加速度はそれぞれ、重力の加速度に等しい。





 fracdvdt=g





さらに、速度の定義により：

 fracdydt=v







2つの普通のリモコンのシステムを手に入れました。 決めます。







標準のScilabディストリビューションの一部であるode（）関数を使用します。

ドキュメントによると、 odeは次のように定義された明示的な常微分方程式を解きます。





 fracdydt=f（t、y）y（t0）=y0











私たちの場合のように。 一次導関数は左側になければなりません。







DEに2次、3次などの導関数が含まれている場合、置換を導入し、1つの方程式を複数のシステムで変換する必要があります。 実際にやったように。 結局、加速度は座標の2次時間微分であり、そこから1次微分に移動し、置換を導入します-変数「速度」はdy / dtに等しくなります。 つまり

から  fracd2ydt2=g に行きました $ inline $ \ begin {equation *} \ begin {cases} \ frac {dv} {dt} = g \\ \ frac {dy} {dt} = v \ end {cases} \ end {equation *} $ inline $







最後に、コードに移りましょう（ githubへのリンク）。 環境が提供するSciNotesエディター、および他のテキストエディターで作成できます。 グラフィックなしでシェルを起動し、コンソールにコマンドを入力することもできます。 私の意見では、SciNotesはコードの強調表示と開発環境への統合により便利です。







まず、リモートコントロールをScilabの機能として説明する必要があります。 







//,         //vector = [v,y], t -  function dVector = verticalFallingVacuum(t, vector) dVector = zeros(2,1); //   -     dVector(1) = g; //dv/dt = g dVector(2) = vector(1); //dy/dt = v endfunction


次に、初期条件を設定します。 







 //    y0 = [0;0]; //v  x   , /  . t0 = 0; //   t = 0:0.1:260; //  , . (4 20)


次に、ソルバー関数ode（）を呼び出し、上記で作成したすべてを入力に渡します。 







 result = ode(y0,t0,t,verticalFallingVacuum); //


結果として、結果マトリックスには、tで指定された範囲の時間軸のポイントに対応する、指定されたリモートコントロールシステムの必要なソリューション関数の値が含まれます。







グラフィカルな形で何が起こったのか見てみましょう。同時に、コンソールにいくつかのコントロールポイントを表示します。 







 //       plot(t,result(2,:)); //  ,    xtitle("      "); //  //      mprintf("C  50 = %f / \n",result(1,500)*3.6); mprintf("   4.20 = %f  \n",result(2,2600)/1000);


すべて一緒に： 







 g = 9.81; //    / mode(0); //    //,         //vector = [v,y] function dVector=verticalFallingVacuum(t, vector) dVector = zeros(2,1); //   dVector(1) = g; //dv/dt = g dVector(2) = vector(1); //dy/dt = v endfunction //    y0 = [0;0]; //v  x   , /  . t0 = 0; //   t = 0:0.1:260; //  , . (4 20) result = ode(y0,t0,t,verticalFallingVacuum); //  //  plot(t,result(2,:)); xtitle("      ") //      mprintf("C  50 = %f / \n",result(1,500)*3.6); mprintf("   4.20 = %f  \n",result(2,2600)/1000);








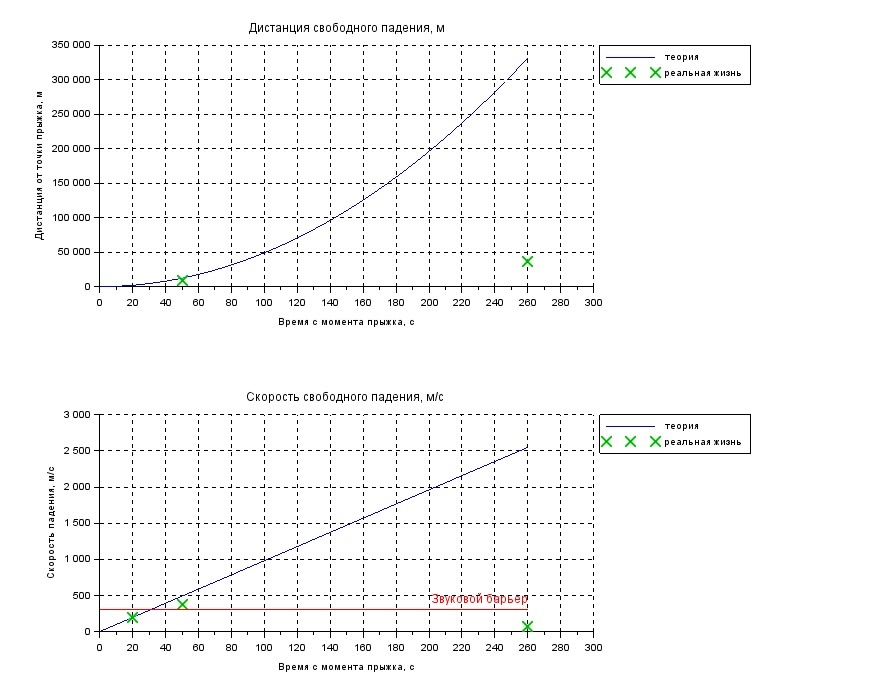
時間に対する座標の予想される二次依存性が得られました。







練習で確認しましょう：

50秒での速度= 1762 km / h（1357 km / hである必要があります）。

4min.20sec = 331.3 km（および36.4 km）で移動した距離。







ジャンプの初期段階で顔をゆがめながら速度に耐えることができる場合、移動距離の合計が1桁超えます。 これは、放出された成層圏のために、飛行の初期段階での不明な空気抵抗が本当に小さく、最も単純なモデルが少なくともそれに対処するからです。しかし、密度が低下すると、大気密度が著しく増加し、落下速度が大幅に低下し、理論に反するようになります。







実験ポイントもプロットするより詳細なグラフを作成すると、このモデルと現実との間の不一致が時間の経過とともに悪化し、さらに明らかになります。 特に、速度は直線的に増加しますが、実際には特定の瞬間から速度が低下し始めます。







改善されたグラフィックを構築する機能

プロッター機能： 







 //         . //t -  1xN     //data -   -  2xN  v,y //realJumpVT -  2N -   -. //realJumpYT -  2xN   -. function [yAxis,vAxis] = drawGraphics (t, data, realJumpVT, realJumpYT) scf();//   xsetech([0 0 0.9 0.47]);// - -       plot2d(t', data(2,:)'); yAxis=gca(); //     yAxis.title.text = "  , "; yAxis.title.font_size=2; //    yAxis.x_label.text = "   , "; yAxis.y_label.text = "   , "; yAxis.grid = [0,0]; //      yAxis.x_location = "origin"; //  x-   yAxis.y_location = "origin"; //  y-   yAxis.children(1).children(1).foreground = 11; //   plot2d(realJumpYT(2,:), realJumpYT(1,:)',[-2]); //   grExpY=gca(); //     grExpY.children(1).children(1).mark_foreground = 14; // -  grExpY.children(1).children(1).thickness = 2; leg1 = legend(["", " "],-1); xsetech([0 0.53 0.9 0.43]);// - -       plot2d(t', data(1,:)'); vAxis=gca(); //     vAxis.title.text = "  , /"; vAxis.title.font_size=2; //    vAxis.x_label.text = "   , "; vAxis.y_label.text = " , /"; vAxis.grid = [0,0]; //      vAxis.x_location = "origin"; //  x-   vAxis.y_location = "origin"; //  y-   vAxis.children(1).children(1).foreground = 11; // -  plot2d(realJumpVT(2,:), realJumpVT(1,:)',[-2]); //   grExpV=gca(); //     grExpV.children(1).children(1).mark_foreground = 14; // -  grExpV.children(1).children(1).thickness = 2; plot2d(t', 300*ones(size(t,'c'),1),[3]); //   grBarrier=gca(); //     grBarrier.children(1).children(1).foreground = 5; // -  xstring(200,320," "); t=get("hdl") //      //t.font_color=21; //  t.font_size=2; leg2 = legend(["", " "],-1); endfunction










空気抵抗力をモデルに導入することで状況を修正します。







モデル-2（空気抵抗を考慮）



大気は力で飛んで作用します





Fair=c cdotS cdotdensity cdot fracv22、







どこで

s-抵抗係数

Sは、飛行方向に垂直な最大断面積です。

密度 -空気密度

vは移動速度です

式はここから取得されます 。分析ソリューションも読むことができます。













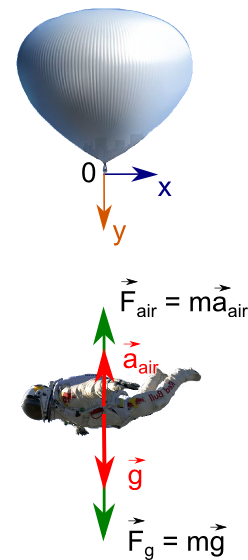
私たちは加速に興味があります（減速と言った方が良いでしょうが）、 F airはシステムの最初の方程式に補正を追加するために極端な飛行を報告します。







ニュートンの第二法則による Fair=m cdota





a= fracFairm= fracc cdotS cdotdeinsity cdotv22 cdotm







この修正により、システムは次の形式になります。

$$ display $$ \ begin {equation *} \ begin {cases} \ frac {dv} {dt} = g-\ frac {1} {m} \ cdot \ frac {c \ cdot S \ cdot deinsity \ cdot v ^ 2} {2} \\ \ frac {dy} {dt} = v \ end {cases} \ end {equation *} $$ display $$











同様の方法で解決します。 リモートコントロールシステムをScilab機能として説明します。 







 //,           //vector = [v,y], t- function dVector = verticalFallingAir(t, vector) dVector = zeros(2,1); //-    height = startHeight-vector(2); //  .     aAir = (0.5*c*airDensity(height)*S*vector(1)^2)/m; //""      dVector(1) = g - aAtm; //dv/dt = g - aAtm dVector(2) = vector(1); //dy/dt = v endfunction


大気の密度は高度によって異なるため、適切な関数を記述する必要があります。 ここから表を取ってください 。 一般的に、GOST 4401-81があります。雰囲気は標準です。 パラメーター（変更N 1を使用）。 







 //      function density = airDensity(height) hVSdensity = [ 0 1.225; 50 1.219; 100 1.213; 200 1.202; 300 1.190; 500 1.167; 1000 1.112; 2000 1.007; 3000 0.909; 4000 0.819; 5000 0.736; 8000 0.526; 10000 0.414; 12000 0.312; 15000 0.195; 20000 0.089; 50000 1.027*10^(-3); 100000 5.550*10^(-7); 120000 2.440*10^(-8); ]; //  if (height < 0) then height = 0; end //        density = interpln(hVSdensity',[height]); endfunction


初期条件を設定して解決します。 







 //    step = 0.1; y0 = [0;0]; //v  x   , /  . t0 = 0; //   t = 0:step:260; //  , . (4 20) result = ode(y0,t0,t,verticalFallingAir); //


グラフを作成して、何が起こったのかを確認します。













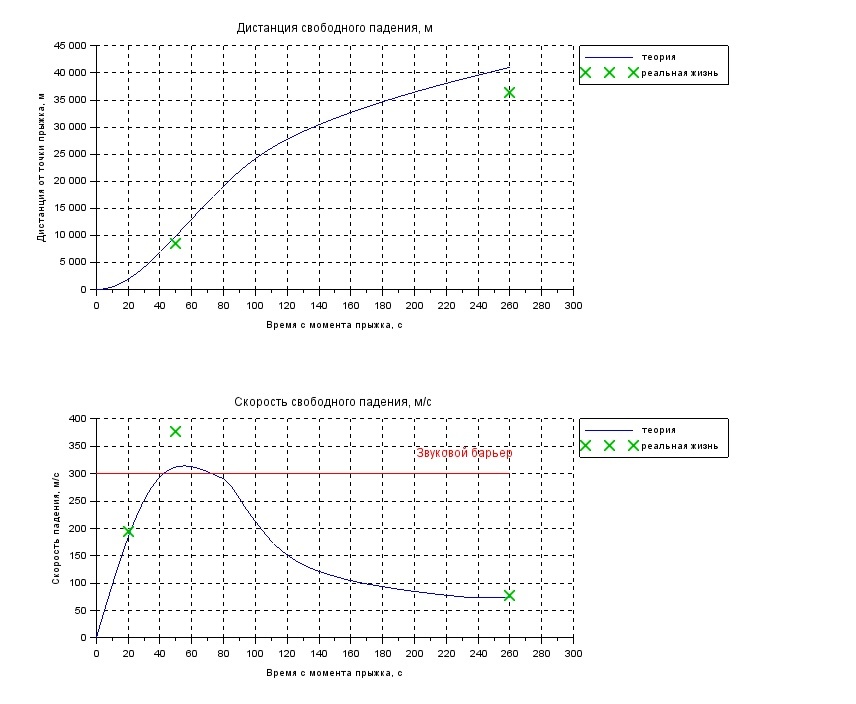
40秒から70秒の間に遮音壁を突破し、50秒の領域で速度が最大に達し、その後速度が低下し始めることがわかります。 獲得した速度は大気中で燃えるほどではなく（Habréで説明）、さらに飛行の終わりまでに、速度はパラシュートを安全に開くことができる値まで低下します。 これは現実に対応しています。







速度-制御点での理論と実験の比較





セントフォールタイム、s 推定速度、m / s 実際の速度、m / s
20 183 194
50 312 377
260 73 77





ホーリーフォール距離-制御点での理論と実験の比較





セントフォールタイム、s 推定距離、m 実際の距離、m
50 9853 8447
260 41049 36403





速度の点では、エラーは平均30 mの自由落下距離（実際の記録の7％）で平均27 m / sです（光の落下で実際に通過した距離の8％）。 トレーニングとデモンストレーションの目的では、まったく問題ありません。







おわりに



したがって、私たちはシンプルだが視覚的なマットの例に取り組んでいます。 モデルは、Scilabを使用してリモートコントロールを解決し、グラフを補間および構築する方法を検討しました。 この記事が初心者がScilabを学ぶのに役立つことを願っています。そして、誰かがScilabの実践でScilabのさらなる使用を奨励するかもしれません。









More articles:


All Articles