オープン機械学習コース。 テーマ7.教師なしで学習：PCAとクラスタリング

みなさんこんにちは！ オープンマシンラーニングコースの7番目のトピックを学習してください。

このレッスンでは、教師なし学習方法、特に主成分分析（PCA）とクラスタリング方法に専念します。 データ内の次元を削減する理由、その方法、およびデータ内の同様の観測をグループ化する方法について学習します。

UPD：現在、コースは英語で、 mlcourse.aiというブランド名で、Medium に関する記事 、Kaggle（ Dataset ）およびGitHubに関する資料があります 。

オープンコースの2回目の立ち上げ（2017年9月から11月）の一環として、この記事に基づいた講義のビデオ 。

この記事の概要

1. 主成分法（PCA）
   
   
   • 直感、理論、およびアプリケーション機能
   • 使用例
2. クラスタリング
   
   
   • K-means
   • アフィニティ伝播
   • スペクトルクラスタリング
   • 凝集クラスタリング
   • クラスタリング品質メトリック
3. 宿題
4. 有用なソース

0.はじめに

教師なしの教育方法と機械学習の通常の分類と回帰の主な違いは、この場合データのマークアップがないことです。 これにより、いくつかの機能が一度に形成されます-第一に、トレーニングのために手でマークアップする必要がないため、異種の大量のデータを使用する可能性、そして第二に、同じ簡単で直感的なメトリックがないため、メソッドの品質を測定する不確実性です教師に課題を教えるときのように。

明示的なマークアップがない場合に頭の中で発生する最も明白なタスクの1つは、データの次元を減らすタスクです。 一方で、それはデータの視覚化の補助と見なすことができます;このために、t-SNEメソッドがよく使用されます。 一方、このような次元の減少は、観測から余分な相関特徴を削除し、教師によるトレーニングモードでのさらなる処理のためにデータを準備できます。たとえば、決定ツリーの入力データをより「消化可能」にします。

1.主成分法（PCA）

直感、理論、およびアプリケーション機能

主成分分析法は、データの次元を削減し、それらを特徴の直交部分空間に射影するための最も直感的にシンプルで頻繁に使用される方法の1つです。

非常に一般的な形では、これは、すべての観測が元の空間の部分空間にある楕円のように見え、この空間の新しい基底がこの楕円の軸と一致するという仮定として表すことができます。 この仮定により、私たちが投影する空間の基底ベクトルは直交するため、強く相関した符号を同時に取り除くことができます。

一般的な場合、この楕円体の次元は元の空間の次元に等しくなりますが、データがより小さい次元の部分空間にあると仮定すると、新しい投影の「余分な」部分空間、つまり楕円が最も伸びない軸に沿った部分空間を破棄できます。 これを「貪欲に」行い、新しい部分空間の基礎の新しい要素として、分散が最大になる楕円体の軸を残りのものから順に選択します。

「14次元空間の超平面に対処するには、3D空間を視覚化し、「14」と非常に大きな声で言います。誰もがそれを行います。」 -ジェフリーヒントン

これが数学的にどのように行われるかを考えてみましょう：

データの次元を減らすために $$$n$ で $$$k、k \ leq n$ トップを選択する必要があります $$$k$ そのような楕円体の軸は、軸に沿った分散によって降順にソートされます。

元の特徴の分散と共分散を計算することから始めましょう。 これは単に共分散行列を使用して行われます。 共分散の定義により、2つの特徴 $$$X_i$ そして $$$X_j$ それらの共分散は

$$

$$cov（X_i、X_j）= E [（X_i-\ mu_i）（X_j-\ mu_j）] = E [X_i X_j]-\ mu_i \ mu_j$$

どこで $$$\ mu_i$ -期待 $$$i$ 番目のサイン。

共分散は対称であり、ベクトルとそれ自体の共分散はその分散に等しくなることに注意してください。

したがって、共分散行列は対称行列であり、対応する特徴の分散は対角線上にあり、対応する特徴の対の共分散は対角線の外側にあります。 マトリックス形式で、ここで $$$\ mathbf {X}$ これは観測行列であり、共分散行列は次のようになります

$$

$$\シグマ= E [（\ mathbf {X}-E [\ mathbf {X}]）（\ mathbf {X}-E [\ mathbf {X}] ^ {T}]$$

メモリを更新するには-線形演算子のような行列には、固有値や固有ベクトル（固有値や固有ベクトル）などの興味深い特性があります。 これらのことは、マトリックスが対応する線形空間に作用するとき、固有ベクトルが所定の位置に残り、対応する固有値で乗算されるという点で注目に値します。 つまり、この行列は、この行列が線形演算子として機能するときに、所定の位置にとどまるか、「自身に入る」部分空間を定義します。 正式に所有するベクトル $$$w_i$ 固有値あり $$$\ lambda_i$ マトリックス用 $$$M$ 単純に $$$M w_i = \ lambda_i w_i$ 。

サンプルの共分散行列 $$$\ mathbf {X}$ 作品として表すことができます $$$\ mathbf {X} ^ {T} \ mathbf {X}$ 。 レイリーの関係から、最大固有値に対応するこの行列の固有ベクトルに沿ってデータセットの最大変動が達成されることがわかります。 したがって、データを投影する主なコンポーネントは、対応するトップの単純な固有ベクトルです $$$k$ この行列の固有値の断片。

それ以降の手順は簡単です。データマトリックスにこれらのコンポーネントを掛けるだけで、これらのコンポーネントの直交ベースでデータを投影できます。 ここで、データマトリックスと主要コンポーネントのベクトルのマトリックスを転置すると、コンポーネントに投影した空間に元のサンプルが復元されます。 コンポーネントの数がソース空間の次元より少ない場合、この変換の情報の一部が失われます。

使用例

アイリスの花のデータセット

scikit-learnパッケージのドキュメントの例に従って、必要なすべてのモジュールをロードし、通常のデータセットをアヤメでひねりましょう。

import numpy as np import matplotlib.pyplot as plt import seaborn as sns; sns.set(style='white') %matplotlib inline from sklearn import decomposition from sklearn import datasets from mpl_toolkits.mplot3d import Axes3D #    iris = datasets.load_iris() X = iris.data y = iris.target #     fig = plt.figure(1, figsize=(6, 5)) plt.clf() ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134) plt.cla() for name, label in [('Setosa', 0), ('Versicolour', 1), ('Virginica', 2)]: ax.text3D(X[y == label, 0].mean(), X[y == label, 1].mean() + 1.5, X[y == label, 2].mean(), name, horizontalalignment='center', bbox=dict(alpha=.5, edgecolor='w', facecolor='w')) #    ,     y_clr = np.choose(y, [1, 2, 0]).astype(np.float) ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y_clr, cmap=plt.cm.spectral) ax.w_xaxis.set_ticklabels([]) ax.w_yaxis.set_ticklabels([]) ax.w_zaxis.set_ticklabels([])
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、PCAがモデルの結果をどのように改善するかを見てみましょう。この場合、データを記述するのに十分な複雑さがないため、分類にはうまくいきません。

 from sklearn.tree import DecisionTreeClassifier from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score, roc_auc_score #       X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.3, stratify=y, random_state=42) #       clf = DecisionTreeClassifier(max_depth=2, random_state=42) clf.fit(X_train, y_train) preds = clf.predict_proba(X_test) print('Accuracy: {:.5f}'.format(accuracy_score(y_test, preds.argmax(axis=1))))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 Out: Accuracy: 0.88889
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで同じことを試してみましょう。ただし、ディメンションを2Dに縮小したデータを使用します。

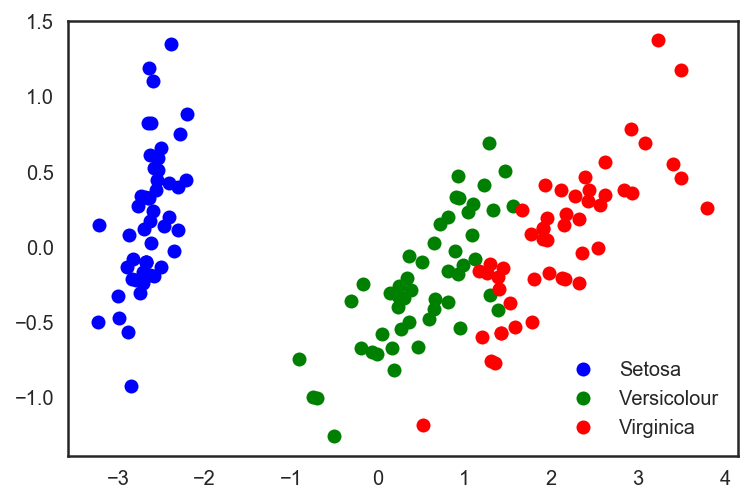
 #    sklearn PCA pca = decomposition.PCA(n_components=2) X_centered = X - X.mean(axis=0) pca.fit(X_centered) X_pca = pca.transform(X_centered) #         plt.plot(X_pca[y == 0, 0], X_pca[y == 0, 1], 'bo', label='Setosa') plt.plot(X_pca[y == 1, 0], X_pca[y == 1, 1], 'go', label='Versicolour') plt.plot(X_pca[y == 2, 0], X_pca[y == 2, 1], 'ro', label='Virginica') plt.legend(loc=0);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 #          . X_train, X_test, y_train, y_test = train_test_split(X_pca, y, test_size=.3, stratify=y, random_state=42) clf = DecisionTreeClassifier(max_depth=2, random_state=42) clf.fit(X_train, y_train) preds = clf.predict_proba(X_test) print('Accuracy: {:.5f}'.format(accuracy_score(y_test, preds.argmax(axis=1))))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

分類精度の向上を確認します。

 Out: Accuracy: 0.91111
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

品質はわずかに向上していることがわかりますが、データが1つの属性に沿って自明に分割されていない、より高次元のより複雑なデータの場合、PCAを使用すると、それらに基づく決定ツリーとアンサンブルの作業の品質を大幅に改善できます。

データの最後のPCA表現の2つの主要なコンポーネントと、それらが「説明する」データの元の分散の割合を見てみましょう。

 for i, component in enumerate(pca.components_): print("{} component: {}% of initial variance".format(i + 1, round(100 * pca.explained_variance_ratio_[i], 2))) print(" + ".join("%.3f x %s" % (value, name) for value, name in zip(component, iris.feature_names)))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 1 component: 92.46% of initial variance 0.362 x sepal length (cm) + -0.082 x sepal width (cm) + 0.857 x petal length (cm) + 0.359 x petal width (cm) 2 component: 5.3% of initial variance 0.657 x sepal length (cm) + 0.730 x sepal width (cm) + -0.176 x petal length (cm) + -0.075 x petal width (cm)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

手書き数値データセット

次に、手書きのデータセットを取得します。 決定木と最近傍の方法についての記事 3で彼と既に協力しました。

 digits = datasets.load_digits() X = digits.data y = digits.target
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これらの数字がどのように見えるかを思い出してください-最初の10を見てください。 ここの写真は、8 x 8マトリックス（各ピクセルの白色強度）で表されています。 さらに、この行列は長さ64のベクトルに「拡張」され、オブジェクトの特性記述が取得されます。

 # f, axes = plt.subplots(5, 2, sharey=True, figsize=(16,6)) plt.figure(figsize=(16, 6)) for i in range(10): plt.subplot(2, 5, i + 1) plt.imshow(X[i,:].reshape([8,8]));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

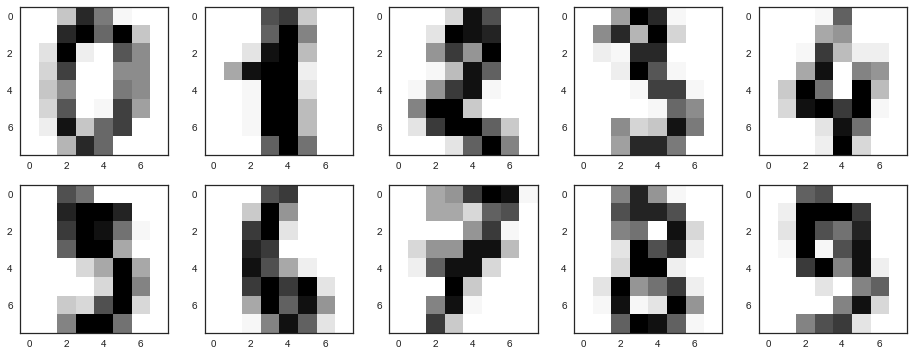
ここでの属性空間の次元は64であることがわかります。しかし、次元をちょうど2に減らして、手書きの数字が目で見てもクラスターにうまく分割されていることを見てみましょう。

 pca = decomposition.PCA(n_components=2) X_reduced = pca.fit_transform(X) print('Projecting %d-dimensional data to 2D' % X.shape[1]) plt.figure(figsize=(12,10)) plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y, edgecolor='none', alpha=0.7, s=40, cmap=plt.cm.get_cmap('nipy_spectral', 10)) plt.colorbar() plt.title('MNIST. PCA projection')
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

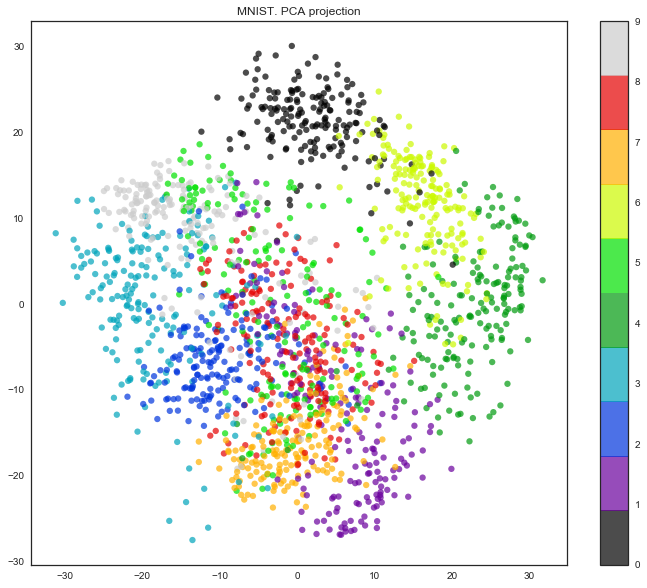
実は、t-SNEを使用すると、PCAには制限があり、元の特徴の線形結合のみが検出されるため、画像はさらに良くなります。 しかし、この比較的小さなデータセットを使用しても、t-SNEがどれだけ長く動作するかがわかります。

 %%time from sklearn.manifold import TSNE tsne = TSNE(random_state=17) X_tsne = tsne.fit_transform(X) plt.figure(figsize=(12,10)) plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y, edgecolor='none', alpha=0.7, s=40, cmap=plt.cm.get_cmap('nipy_spectral', 10)) plt.colorbar() plt.title('MNIST. t-SNE projection')
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

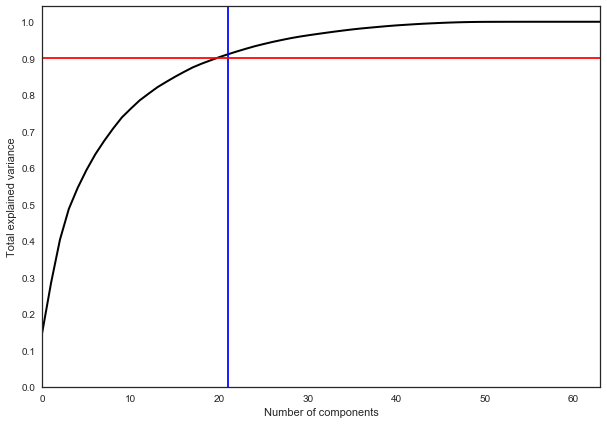
実際には、原則として、ソースデータの分散の90％を残すように多くの主要コンポーネントが選択されます。 この場合、21個の主要コンポーネントを選択するだけで十分です。つまり、寸法を64個のフィーチャから21個に減らします。

 pca = decomposition.PCA().fit(X) plt.figure(figsize=(10,7)) plt.plot(np.cumsum(pca.explained_variance_ratio_), color='k', lw=2) plt.xlabel('Number of components') plt.ylabel('Total explained variance') plt.xlim(0, 63) plt.yticks(np.arange(0, 1.1, 0.1)) plt.axvline(21, c='b') plt.axhline(0.9, c='r') plt.show();
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

2.クラスタリング

クラスタリング問題の直観的な記述は非常に単純であり、「ここにポイントを注ぎました。それらはいくつかのヒープに積み上げられていることがわかります。新しいポイントの場合、これらのポイントをヒープに関連付けることができればクールです」どの平面に落ちるかを言う平面上のポイント。」 この声明から想像力の余地があることが明らかであり、これからこの問題を解決するための対応するアルゴリズムのセットが生じます。 リストされたアルゴリズムは、このセットを完全に説明するものではありませんが、クラスタリングの問題を解決する最も一般的な方法の例です。

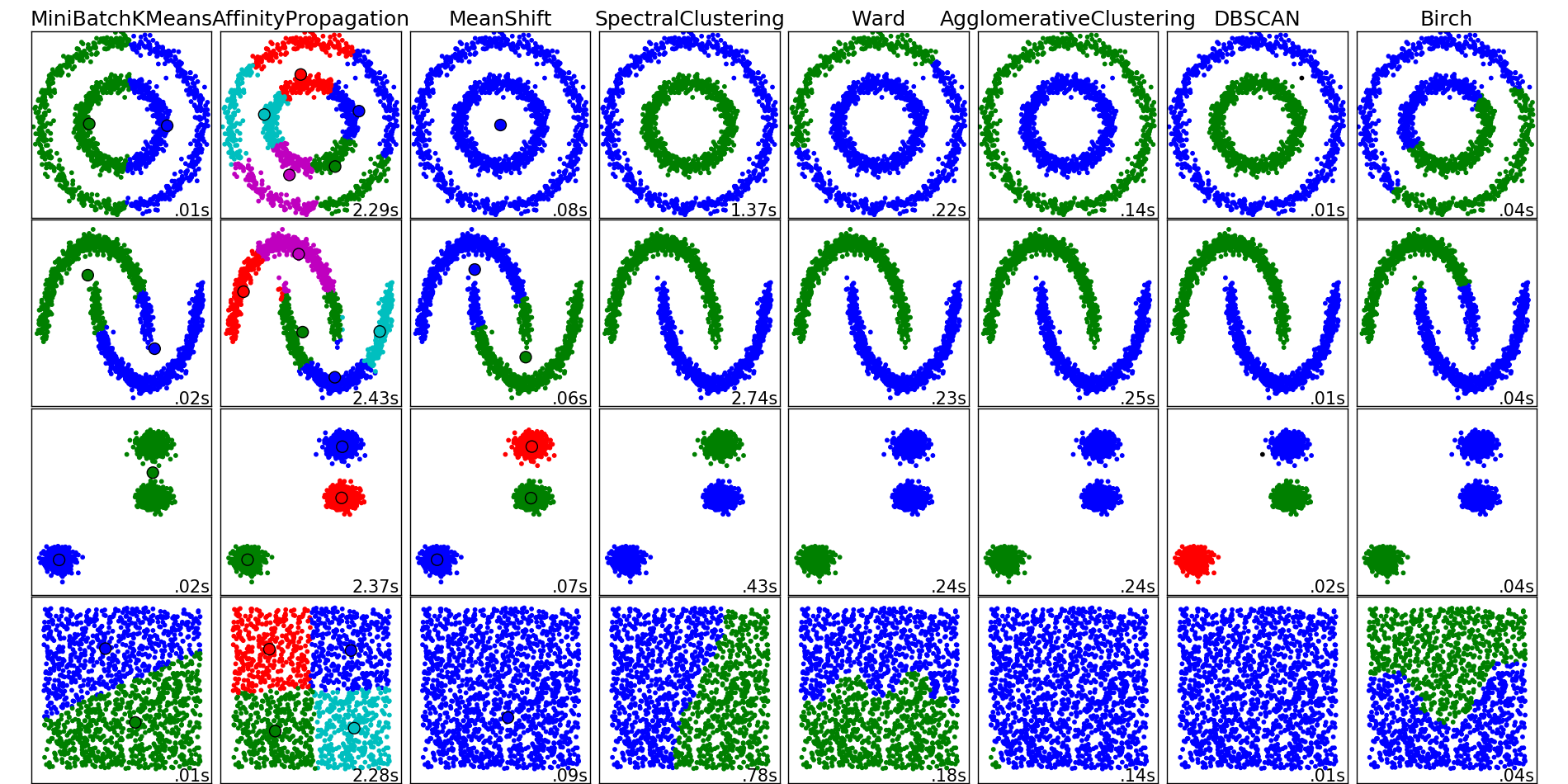
scikit-learnパッケージのドキュメントのクラスタリングアルゴリズムの例

K-means

K-meansアルゴリズムは、おそらく最も一般的で単純なクラスタリングアルゴリズムであり、単純な擬似コードとして非常に簡単に表現できます。

1. クラスターの数を選択します $$$k$ これはデータにとって最適なようです。
2. データのスペースにランダムに注ぐ $$$k$ ポイント（重心）。
3. データセットの各ポイントについて、どの重心に近いかを計算します。
4. 各重心を、この重心に起因するサンプルの中心に移動します。
5. 最後の2つのステップを一定回数繰り返すか、重心が「収束」するまで繰り返します（通常、これは前の位置に対する相対変位が所定の小さな値を超えないことを意味します）。

平面上にあるポイントの通常のユークリッドメトリックの場合、このアルゴリズムは分析的に署名して描画するのが非常に簡単です。 対応する例を見てみましょう：

 #   ,        X = np.zeros((150, 2)) np.random.seed(seed=42) X[:50, 0] = np.random.normal(loc=0.0, scale=.3, size=50) X[:50, 1] = np.random.normal(loc=0.0, scale=.3, size=50) X[50:100, 0] = np.random.normal(loc=2.0, scale=.5, size=50) X[50:100, 1] = np.random.normal(loc=-1.0, scale=.2, size=50) X[100:150, 0] = np.random.normal(loc=-1.0, scale=.2, size=50) X[100:150, 1] = np.random.normal(loc=2.0, scale=.5, size=50) plt.figure(figsize=(5, 5)) plt.plot(X[:, 0], X[:, 1], 'bo');
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

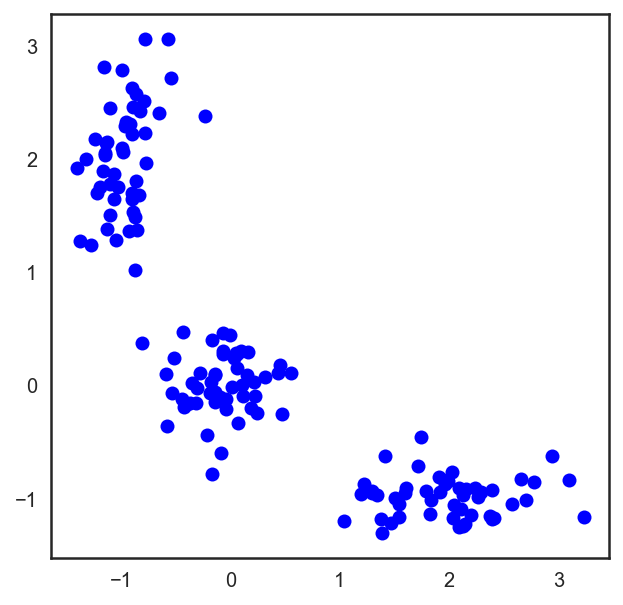
 #  scipy   ,    #      ,     from scipy.spatial.distance import cdist #          np.random.seed(seed=42) centroids = np.random.normal(loc=0.0, scale=1., size=6) centroids = centroids.reshape((3, 2)) cent_history = [] cent_history.append(centroids) for i in range(3): #       distances = cdist(X, centroids) # ,        labels = distances.argmin(axis=1) #          centroids = centroids.copy() centroids[0, :] = np.mean(X[labels == 0, :], axis=0) centroids[1, :] = np.mean(X[labels == 1, :], axis=0) centroids[2, :] = np.mean(X[labels == 2, :], axis=0) cent_history.append(centroids)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

 #       plt.figure(figsize=(8, 8)) for i in range(4): distances = cdist(X, cent_history[i]) labels = distances.argmin(axis=1) plt.subplot(2, 2, i + 1) plt.plot(X[labels == 0, 0], X[labels == 0, 1], 'bo', label='cluster #1') plt.plot(X[labels == 1, 0], X[labels == 1, 1], 'co', label='cluster #2') plt.plot(X[labels == 2, 0], X[labels == 2, 1], 'mo', label='cluster #3') plt.plot(cent_history[i][:, 0], cent_history[i][:, 1], 'rX') plt.legend(loc=0) plt.title('Step {:}'.format(i + 1));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

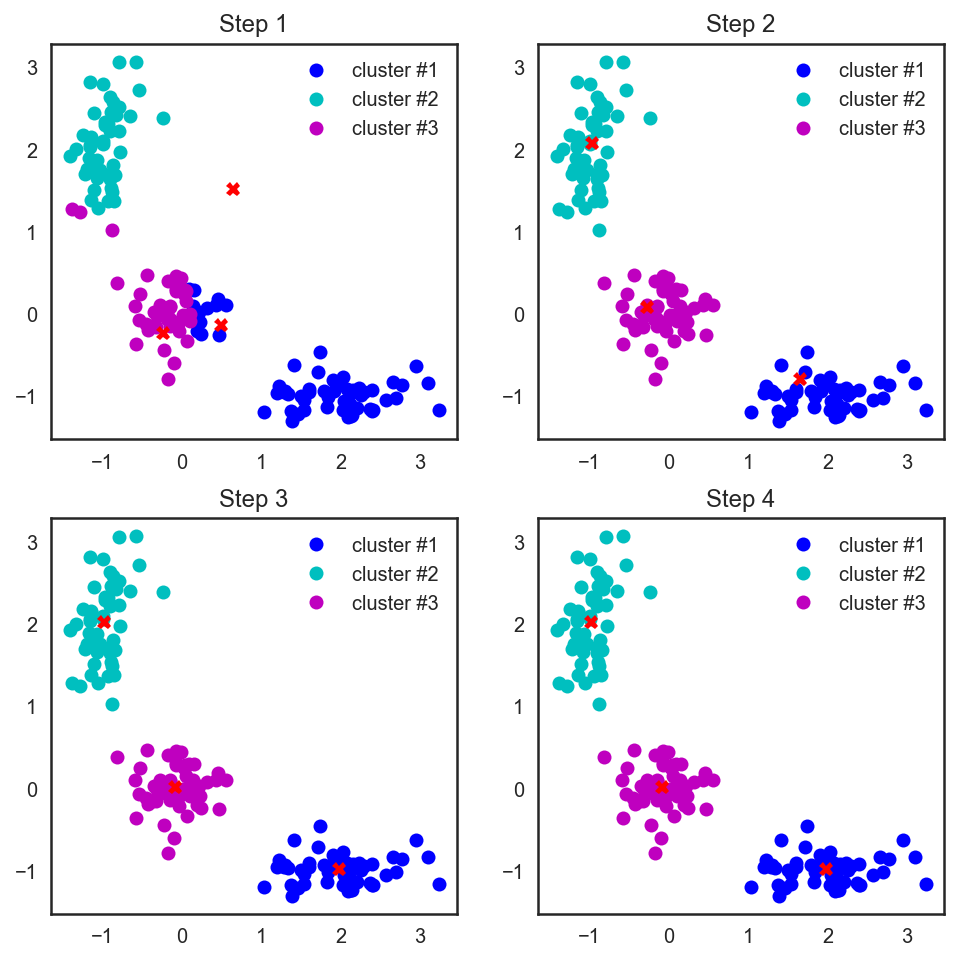
また、ユークリッド距離を考慮しましたが、アルゴリズムは他のメトリックの場合に収束するため、データに応じて、さまざまなクラスタリングタスクについて、ステップ数または収束基準だけでなく、クラスターのポイントと重心間の距離を考慮します。

このアルゴリズムのもう1つの特徴は、空間内の重心クラスターの初期位置に敏感であることです。 この状況では、アルゴリズムの連続した実行を数回保存し、結果として生じるクラスターの後続の平均化を行います。

kMeansのクラスター数の選択

分類または回帰の問題とは異なり、クラスタリングの場合、クラスタリングの問題を最適化問題として提示するのが簡単な基準を選択することはより困難です。

kMeansの場合、このような基準は一般的です。つまり、ポイントからそれらが関連するクラスターの重心までの距離の2乗の合計です。

$$

$$J（C）= \ sum_ {k = 1} ^ K \ sum_ {i〜\ in〜C_k} || x_i-\ mu_k || ^ {2} \ rightarrow \ min \ limits_C、$$

こっち $$$C$ -多くの電源クラスター $$$K$ 、 $$$\ mu_k$ -クラスター重心 $$$C_k$ 。

これには常識があることは明らかです。ポイントをクラスターの中心近くに配置する必要があります。 ただし、問題があります。ポイントと同じ数のクラスターがある場合（つまり、各ポイントが1つの要素のクラスターである場合）、そのような機能の最小値が達成されます。

この問題を解決する（クラスターの数を選択する）ために、ヒューリスティックがよく使用されます。つまり、説明されている関数が始まるクラスターの数を選択します。 $$$J（C）$ 「それほど速くない」。 またはより正式に：

$$

$$D（k）= \ frac {| J（C_k）-J（C_ {k + 1}）|} {| J（C_ {k-1}）-J（C_k）|} \ rightarrow \ min \ limits_k$$

例を考えてみましょう。

 from sklearn.cluster import KMeans inertia = [] for k in range(1, 8): kmeans = KMeans(n_clusters=k, random_state=1).fit(X) inertia.append(np.sqrt(kmeans.inertia_)) plt.plot(range(1, 8), inertia, marker='s'); plt.xlabel('$k$') plt.ylabel('$J(C_k)$');
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

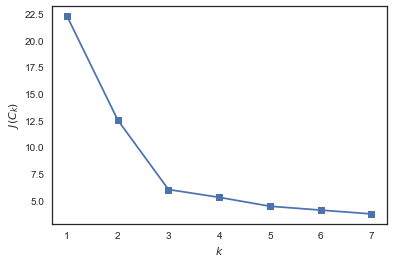
私たちはそれを見る $$$J（C_k）$ クラスターの数が1から2および2から3に増加すると、大幅に減少しますが、変更ではそれほど多くありません $$$k$ したがって、この問題では、3つのクラスターを指定することが最適です。

難しさ

K-means問題自体の解決策はNP困難であり、次元 $$$d$ 、クラスターの数 $$$k$ およびポイント数 $$$n$ 決めた $$$O（n ^ {d k + 1}）$ 。 このような痛みを解決するために、たとえば、トレーニングではデータセット全体を使用せず、その小さな部分（バッチ）のみを使用して、それに関連するすべてのポイントからの重心更新の履歴全体の平均を使用して重心を更新する、ミニバッチK平均などのヒューリスティックがよく使用されます。 通常のK-meansとそのMiniBatch実装の比較は、 scikit-learnのドキュメントに記載されています 。

scikit-learn でのアルゴリズムの実装には 、 n_init



パラメーターを使用して開始数を設定する機能など、便利なn_init



が多数あります。これにより、データが歪んだ場合にクラスターの安定した重心が得られます。 さらに、これらの起動は、計算時間を犠牲にすることなく並行して実行できます。

アフィニティ伝播

クラスタリングアルゴリズムの別の例。 K-meansアルゴリズムとは異なり、このアプローチでは、データを分割するクラスターの数を事前に決定する必要はありません。 アルゴリズムの主な考え方は、観測値がグループ内で「通信」する方法またはそれらが互いにどの程度類似しているかに基づいてクラスター化することです。

このために、「類似性」のメトリックを紹介します。 $$$s（x_i、x_j）> s（x_i、x_k）$ 観察するなら $$$x_i$ 観察のように $$$x_j$ 上より $$$x_k$ 。 この類似性の簡単な例は、距離の負の二乗です $$$s（x_i、x_j）=-|| x_i-x_j || ^ {2}$ 。

次に、「通信」のプロセスについて説明します。 これを行うために、ゼロに初期化された2つの行列があり、そのうちの1つは $$$r_ {i、k}$ どのくらいうまく説明します $$$k$ 2番目の観察結果は、 $$$i$ 他のすべての潜在的な「例」に関する1つの観察結果と、 $$$a_ {i、k}$ それがいかに正しいかを説明します $$$i$ 選択する観察 $$$k$ そのような「例」として2番目。 少しわかりにくいかもしれませんが、もう少し「指で」例を見てみましょう。

その後、ルールに従ってマトリックスデータが順番に更新されます。

$$

$$r_ {i、k} \ leftarrow s_（x_i、x_k）-\ max_ {k '\ neq k} \ left \ {a_ {i、k'} + s（x_i、x_k '）\ right \}$$

$$

$$a_ {i、k} \ leftarrow \ min \ left（0、r_ {k、k} + \ sum_ {i '\ not \ in \ {i、k \}} \ max（0、r_ {i'、 k}）\右）、\ \ \ i \ neq k$$

$$

$$a_ {k、k} \左矢印\ sum_ {i '\ neq k} \ max（0、r_ {i'、k}）$$

スペクトルクラスタリング

スペクトルクラスタリングは、上記のいくつかのアプローチを組み合わせて、初期空間よりも小さい次元の複雑な多様体から最大の利益を得ます。

このアルゴリズムが機能するには、隣接行列を決定する必要があります。 上記のアフィニティ伝播の場合と同じ方法でこれを行うことができます。 $$$A_ {i、j} =-|| x_i-x_j || ^ {2}$ 。 このマトリックスは、観測値に頂点があり、観測値の各ペア間のエッジが、これらの頂点の類似度に対応する重みを持つ完全なグラフも記述します。 上記の選択されたメトリックと平面上にあるポイントの場合、このことは直感的でシンプルになります。2つのポイントは、それらの間のエッジが短いほど似ています。 次に、結果のグラフを2つの部分に分割して、2つのグラフの結果のポイントが、「その他」の半分のポイントよりも、グラフの「それらの」半分の内側の他のポイントにより一般的に似るようにします。 このようなタスクの正式な名前は、ノーマライズドカット問題と呼ばれます 。これについては、 こちらを参照してください 。

凝集クラスタリング

おそらく、クラスターの数が固定されていない最も単純で最も理解しやすいクラスタリングアルゴリズムは、凝集クラスタリングです。 アルゴリズムの直感は非常に簡単です。

1. 各ポイントにクラスターを注ぐことから始めます
2. クラスターの中心間のペアワイズ距離を昇順に並べ替えます
3. いくつかの近くのクラスターを取り、それらを1つに接着し、クラスターの中心を数えます
4. すべてのデータが1つのクラスターに接着されるまで、手順2と3を繰り返します。

最も近いクラスターを見つけるプロセスは、ポイントを結合するさまざまな方法を使用して実行できます。

1. 単一リンケージ-2つのクラスターからのポイント間の最小ペアワイズ距離
   
   $$$d（C_i、C_j）= min_ {C_iのx_i \、C_jのx_j \} || x_i-x_j ||$
2. 完全なリンケージ-2つのクラスターからのポイント間の最大ペアワイズ距離
   
   $$$d（C_i、C_j）= max_ {C_iのx_i \、C_jのx_j \} || x_i-x_j ||$
3. 平均リンケージ-2つのクラスターのポイント間の平均ペアワイズ距離
   
   $$$d（C_i、C_j）= \ frac {1} {n_i n_j} \ sum_ {x_i \ in C_i} \ sum_ {x_j \ in C_j} || x_i-x_j ||$
4. 重心リンケージ-2つのクラスターの重心間の距離
   
   $$$d（C_i、C_j）= || \ mu_i-\ mu_j ||$

4番目と比較して最初の3つのアプローチの利点は、接着後に毎回距離を再計算する必要がないことです。これにより、アルゴリズムの計算の複雑さが大幅に軽減されます。

このようなアルゴリズムの結果に基づいて、すばらしいクラスターグルーツリーを構築し、それを見て、アルゴリズムを停止するのに最適な段階を判断することもできます。 または、k-meansと同じエルボルールを使用します。

幸いなことに、Pythonにはすでに、凝集クラスター化のためのこのような樹状図を作成するための優れたツールがあります。 K-meansからのクラスターの例を考えてみましょう。

 from scipy.cluster import hierarchy from scipy.spatial.distance import pdist X = np.zeros((150, 2)) np.random.seed(seed=42) X[:50, 0] = np.random.normal(loc=0.0, scale=.3, size=50) X[:50, 1] = np.random.normal(loc=0.0, scale=.3, size=50) X[50:100, 0] = np.random.normal(loc=2.0, scale=.5, size=50) X[50:100, 1] = np.random.normal(loc=-1.0, scale=.2, size=50) X[100:150, 0] = np.random.normal(loc=-1.0, scale=.2, size=50) X[100:150, 1] = np.random.normal(loc=2.0, scale=.5, size=50) distance_mat = pdist(X) # pdist        Z = hierarchy.linkage(distance_mat, 'single') # linkage —    plt.figure(figsize=(10, 5)) dn = hierarchy.dendrogram(Z, color_threshold=0.5)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

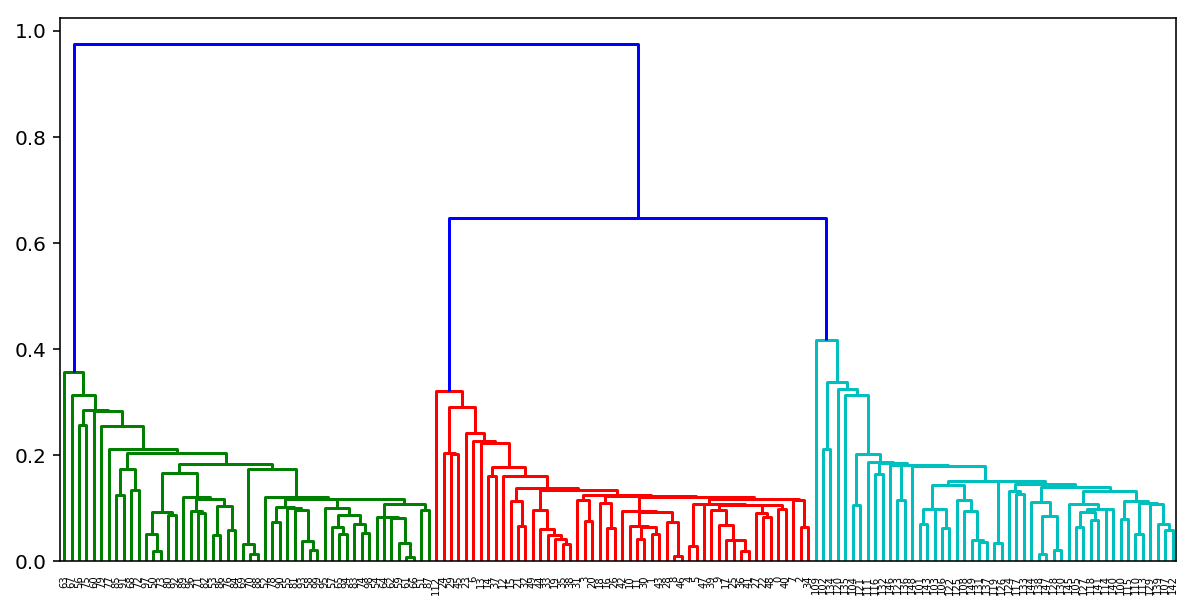
クラスタリング品質メトリック

クラスタリングの品質を評価するタスクは、分類の品質を評価するよりも複雑です。 まず、このような推定値はラベル値自体に依存するのではなく、サンプル自体のパーティションにのみ依存する必要があります。 第二に、オブジェクトの真のラベルは常にわかっているとは限らないため、未割り当てのサンプルのみを使用してクラスタリングの品質を評価するために推定値も必要です。

外部および内部の品質指標を強調します。 外部のものは真のクラスター化に関する情報を使用しますが、内部メトリックは外部情報を使用せず、データセットのみに基づいてクラスタリングの品質を評価します。 通常、クラスターの最適な数は、内部メトリックを使用して決定されます。

以下のすべてのメトリックは、 sklearn.metrics



実装されsklearn.metrics



。

調整されたランドインデックス（ARI）

真のオブジェクトラベルは既知であると想定されます。 この測定値はラベル値自体に依存せず、サンプルのクラスターへの分割のみに依存します。 させる $$$n$ -サンプル内のオブジェクトの数。 で示す $$$a$ -同じラベルを持ち、同じクラスター内にあるオブジェクトのペアの数 $$$b$ -異なるラベルを持ち、異なるクラスターにあるオブジェクトのペアの数。 ランドインデックスは

$$

$$\ text {RI} = \ frac {2（a + b）} {n（n-1）}。$$

つまり、これは、これらのパーティション（元のクラスタリングと結果のクラスタリング）が「一貫性がある」オブジェクトの割合です。 ランドインデックス（RI）は、同じサンプルの2つの異なるクラスタリングの類似性を表します。 そのため、このインデックスは、任意の $$$n$ およびクラスターの数、それを正規化する必要があります。 これは、調整済みランドインデックスの定義方法です。

$$

$$\ text {ARI} = \ frac {\ text {RI}-E [\ text {RI}]} {\ max（\ text {RI}）-E [\ text {RI}]$$

この測度は対称的で、ラベル値と順列に依存しません。 したがって、このインデックスは、異なるサンプルパーティション間の距離の尺度です。 $$$\テキスト{ARI}$ 範囲内の値を取ります $$$[-1、1]$ 。 負の値は「独立した」クラスターに対応し、ゼロに近い値はランダムなパーティションに対応し、正の値は2つのパーティションが類似していることを示します（で一致します） $$$\テキスト{ARI} = 1$ ）

調整された相互情報（AMI）

この尺度は非常に似ています $$$\テキスト{ARI}$ 。 また、対称であり、ラベル値と順列に依存しません。 エントロピー関数を使用して決定され、サンプルのパーティションを離散分布として解釈します（クラスターに割り当てられる確率は、クラスター内のオブジェクトの割合に等しくなります）。 索引 $$$MI$ は、サンプルのクラスターへの分割に対応する2つの分布の相互情報として定義されます。 直感的には、相互情報量は両方のパーティションに共通する情報の割合を測定します。つまり、一方のパーティションに関する情報が他方のパーティションに関する不確実性を減らす量です。

同様に $$$\テキスト{ARI}$ インデックスが決定されます $$$\テキスト{AMI}$ インデックスの成長を取り除く $$$MI$ クラスの数の増加に伴い。 範囲内の値を取ります $$$[0、1]$ 。 ゼロに近い値はパーティションの独立性を示し、ユニティに近い値はそれらの類似性（ $$$\テキスト{AMI} = 1$ ）

均一性、完全性、Vメジャー

正式には、これらの測定値は、エントロピーと条件付きエントロピーの関数を使用して、サンプルのパーティションを離散分布として考慮して決定されます。

$$

$$h = 1-\ frac {H（C \ mid K）} {H（C）}、c = 1-\ frac {H（K \ mid C）} {H（K）}、$$

こっち $$$K$ -クラスタリングの結果、 $$$C$ -サンプルのクラスへの真の分割。 このように $$$h$ 各クラスが同じクラスのオブジェクトで構成される量を測定します。 $$$c$ -同じクラスのオブジェクトが同じクラスターにどこまで属するか。 これらの測定値は対称的ではありません。 両方の値は、範囲内の値を取ります $$$[0、1]$ 、より大きな値はより正確なクラスタリングに対応します。 これらの測定値は、次のように正規化されていません。 $$$\テキスト{ARI}$ または $$$\テキスト{AMI}$ 、したがってクラスターの数に依存します。 ランダムクラスタリングは、多数のクラスと少数のオブジェクトでゼロメトリックを生成しません。 これらの場合、使用することが望ましい $$$\text{ARI}$ 。 ただし、オブジェクトの数が1000を超え、クラスターの数が10未満の場合、この問題はそれほど顕著ではなく、無視できます。

両方の数量を計上するには $$$h$ そして $$$c$同時に入力$$$V$調和平均としての測定：

$$

$$v = 2\frac{hc}{h+c}.$$

これは対称的であり、2つのクラスターがどのように類似しているかを示しています。

シルエット

, , , () . . $$$a$ — , $$$b$ — ( , ). :

$$

$$s = \frac{b - a}{\max(a, b)}.$$

サンプルのシルエットは、このサンプルのオブジェクトのシルエットの平均サイズです。したがって、シルエットは、そのクラスターのオブジェクトまでの平均距離が他のクラスターのオブジェクトまでの平均距離とどれだけ異なるかを示します。この値は範囲内にあります$$$[-1、1]$ 。-1に近い値は貧弱な（異種の）クラスタリングに対応し、ゼロに近い値はクラスターが交差して重なり合うことを示し、1に近い値は「密な」明確に識別されたクラスターに対応します。したがって、シルエットが大きいほど、クラスターはより明確になり、コンパクトで密にグループ化された点群になります。

シルエットを使用して、最適なクラスター数を選択できます $$$k$ ( ) — , . , , , , .

, MNIST:

 from sklearn import metrics from sklearn import datasets import pandas as pd from sklearn.cluster import KMeans, AgglomerativeClustering, AffinityPropagation, SpectralClustering data = datasets.load_digits() X, y = data.data, data.target algorithms = [] algorithms.append(KMeans(n_clusters=10, random_state=1)) algorithms.append(AffinityPropagation()) algorithms.append(SpectralClustering(n_clusters=10, random_state=1, affinity='nearest_neighbors')) algorithms.append(AgglomerativeClustering(n_clusters=10)) data = [] for algo in algorithms: algo.fit(X) data.append(({ 'ARI': metrics.adjusted_rand_score(y, algo.labels_), 'AMI': metrics.adjusted_mutual_info_score(y, algo.labels_), 'Homogenity': metrics.homogeneity_score(y, algo.labels_), 'Completeness': metrics.completeness_score(y, algo.labels_), 'V-measure': metrics.v_measure_score(y, algo.labels_), 'Silhouette': metrics.silhouette_score(X, algo.labels_)})) results = pd.DataFrame(data=data, columns=['ARI', 'AMI', 'Homogenity', 'Completeness', 'V-measure', 'Silhouette'], index=['K-means', 'Affinity', 'Spectral', 'Agglomerative']) results
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

	ARI	AMI	Homogenity	Completeness	V-measure	Silhouette
K-means	0.662295	0.732799	0.735448	0.742972	0.739191	0.182097
Affinity	0.175174	0.451249	0.958907	0.486901	0.645857	0.115197
Spectral	0.752639	0.827818	0.829544	0.876367	0.852313	0.182195
Agglomerative	0.794003	0.856085	0.857513	0.879096	0.868170	0.178497

3.

, .

- Samsung . , (, ) . Jupyter- , - , .

4.

• Open Machine Learning Course. Topic 7. Unsupervised Learning: PCA and Clustering
• – Medium story
• " "
• " (PCA) "
• " , : Affinity propagation"
• " , : DBSCAN"
• scikit-learn (.)
• Q&A PCA (.)
• k-Means EM- (.)
• " "

yorko ( ). Jupyter GitHub- .