挑戦する
この記事では、SymPyパッケージの機能をNumPyパッケージと組み合わせて使用します。 すべては、文字式を他のPythonモジュールで動作できる関数に変換することです。
微分方程式を解くプロセスは視覚的になり、計算の各段階でうまく制御されます。 さまざまな解釈における振動リンクがネットワーク[1,2]で議論されていることに注意すべきです。 たとえば、[3]では、過渡プロセスの詳細な研究を伴う振動リンクのモデルが提示されています。
Pythonの振動リンクのそのような研究が彼らの支持者を見つけることを願っています。
プログラムコード
読者を飽きさせないために、各重要行の説明とともにプログラムコードをすぐに提供します。
コード
import numpy as np from sympy import * from IPython.display import * import matplotlib.pyplot as plt init_printing(use_latex=True) var('t C1 C2') u = Function("u")(t) # , . m=20 # . w=10.0# . c=0.3# . a=1# . # ( ). t# . de = Eq(m*u.diff(t,t)+w*u.diff(t)+c*u,a) #- . display(de)#- . des = dsolve(de,u)# . display(des)# . eq1=des.rhs.subs(t,0);# t=0. display(eq1)# . eq2=des.rhs.diff(t).subs(t,0)# # t=0. display(eq2)# . seq=solve([eq1,eq2],C1,C2)# C1,C2. display(seq)# . rez=des.rhs.subs([(C1,seq[C1]),(C2,seq[C2])])# # . display(rez)# . f=lambdify(t, rez, "numpy")# # numpy . x = np.arange(0.0,500,0.01) plt.plot(x,f(x),color='b', linewidth=3) plt.xlabel('Time t seconds',fontsize=12) plt.ylabel('$f(t)$',fontsize=16) plt.grid(True) plt.show()
減衰を設定し、非周期運動と方程式を解くすべてのステップを取得します。

Eq(0.3 * u(t)+ 10.0 *導関数(u(t)、t)+ 20 *導関数(u(t)、t、t)、1)
Eq(u(t)、C1 * exp(t *(-5-sqrt(19))/ 20)+ C2 * exp(t *(-5 + sqrt(19))/ 20)+ 3.33333333333333)
C1 + C2 + 3.33333333333333
C1 *(-1/4-sqrt(19)/ 20)+ C2 *(-1/4 + sqrt(19)/ 20)
{C1:0.245131115588015、C2:-3.57846444892135}
0.245131115588015 * exp(t *(-5-sqrt(19))/ 20)-3.57846444892135 * exp(t *(-5 + sqrt(19))/ 20)+ 3.33333333333333
パラメーターを変更し、プログラムリストを書き直して、1つのグラフに減衰を増やしながら3つの動きを表示します。
3つの異なる減衰値のプログラムコード
import numpy as np from sympy import * from IPython.display import * import matplotlib.pyplot as plt init_printing(use_latex=True) var('t C1 C2') u = Function("u")(t) # , . m=200 # . w=1.8# . c=1.3# . a=1# . # ( ). t# . man=[0.8,2.12,5]# ( ). for w in man: de = Eq(m*u.diff(t,t)+w*u.diff(t)+c*u,a) #- . display(de)#- . des = dsolve(de,u)# . display(des)# . eq1=des.rhs.subs(t,0);# t=0. display(eq1)# . eq2=des.rhs.diff(t).subs(t,0)# t=0. display(eq2)# . seq=solve([eq1,eq2],C1,C2)# C1,C2. display(seq)# . rez=des.rhs.subs([(C1,seq[C1]),(C2,seq[C2])])# # . display(rez)# . f=lambdify(t, rez, "numpy")# numpy . x = np.arange(0.0,500,0.01) if w==man[0]:# . plt.plot(x,f(x),color='r', linewidth=3) elif w==man[1]: plt.plot(x,f(x),color='g', linewidth=3) elif w==man[2]: plt.plot(x,f(x),color='b', linewidth=3) plt.xlabel('Time t seconds',fontsize=12) plt.ylabel('$f(t)$',fontsize=16) plt.grid(True) plt.show()
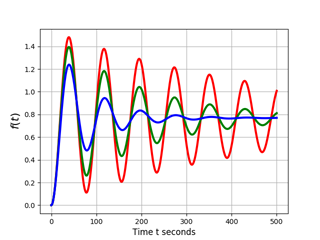
減衰パラメーターの値を設定し、周期的な減衰運動と3つの方程式を解くすべての段階のグラフを取得します。
Eq(1.3 * u(t)+ 0.8 *導関数(u(t)、t)+ 200 *導関数(u(t)、t、t)、1)
Eq(u(t)、(C1 * sin(sqrt(406)* t / 250)+ C2 * cos(sqrt(406)* t / 250))/ exp(t)**(1/500)+ 0.769230769230769 )
C2 + 0.769230769230769
平方根(406)* C1 / 250-C2 / 500
{C2:-0.769230769230769、C1:-0.0190881410379025}
(-0.0190881410379025 * sin(sqrt(406)* t / 250)-0.769230769230769 * cos(sqrt(406)* t / 250))/ exp(t)**(1/500)+ 0.769230769230769
Eq(1.3 * u(t)+ 2.12 *導関数(u(t)、t)+ 200 *導関数(u(t)、t、t)、1)
Eq(u(t)、(C1 * sin(sqrt(647191)* t / 10000)+ C2 * cos(sqrt(647191)* t / 10000))/ exp(t)**(53/10000)+ 0.769230769230769 )
C2 + 0.769230769230769
sqrt(647191)* C1 / 10000-53 * C2 / 10000
{C2:-0.769230769230769、C1:-0.0506776284001243}
(-0.0506776284001243 * sin(sqrt(647191)* t / 10000)-0.769230769230769 * cos(sqrt(647191)* t / 10000))/ exp(t)**(53/10000)+ 0.769230769230769
Eq(1.3 * u(t)+ 5 *導関数(u(t)、t)+ 200 *導関数(u(t)、t、t)、1)
Eq(u(t)、(C1 * sin(sqrt(1015)* t / 400)+ C2 * cos(sqrt(1015)* t / 400))/ exp(t)**(1/80)+ 0.769230769230769 )
C2 + 0.769230769230769
平方(1015)* C1 / 400-C2 / 80
{C2:-0.769230769230769、C1:-0.120724003956605}
(-0.120724003956605 * sin(sqrt(1015)* t / 400)-0.769230769230769 * cos(sqrt(1015)* t / 400))/ exp(t)**(1/80)+ 0.769230769230769
質量指数を減らし、モーショングラフを取得します(削減の方程式の解を見逃します)。

負の減衰の重要なケースを検討し、対応するグラフを取得します(削減の方程式の解を見逃します)。
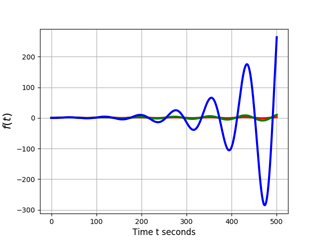
おわりに
得られた振動リンクの動作の図解は、理論と完全に一致しています。
SymPyとNumPyの微分方程式の記号解と数値解により、質量減衰と剛性制御を備えた振動リンクの適切なモデルを作成し、同時に振動方程式の回転を制御することができました。 さらに、Pythonはシェアウェアであり、プログラムを研究および教育目的で使用する可能性を大幅に拡大します。