仕事の目的
私の記事[1]では、非線形要素を含む制御システムを研究するための調和線形化法が検討されています。
この方法は、システムの線形部分がローパスフィルターである場合に使用できます。 最初の高調波を除く、非線形要素の出力で発生するすべての高調波成分を除去します[2]。 したがって、最初の記事の論理的な続きは、考慮される非線形要素の調和解析になります。 さらに、高調波線形化の方法に代わるハードウェアを検討する必要があります。
分析方法とプログラムコード
純粋な正弦波信号が非線形要素に到達するようにします。 離散フーリエ級数に展開する方法により、そのスペクトルを取得します。
#!/usr/bin/env python #coding=utf8 from numpy import array, arange, abs as np_abs from numpy.fft import rfft, rfftfreq from math import sin, pi import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' FD = 250000# , N = 2500# , N/FD F=250.0# w=(2.*pi*F/FD)# A=3.0# B=0.5# # F N sin_sig = array([A*sin(w*t) for t in range(N)])# plt.plot(arange(N)/float(FD), sin_sig, 'r') plt.xlabel(', .') plt.ylabel(' ') plt.title(' ') plt.grid(True) plt.show() spectr_sin = rfft(sin_sig )# rfft plt.plot(rfftfreq(N, 1./FD), np_abs(spectr_sin)/N) # plt.xlabel(', ') plt.ylabel(' ') plt.title(' ') plt.grid(True) plt.show()
「飽和」を伴う非線形要素の出力から信号と信号スペクトルを取得します。
# c «» A*sin(w*t) abs()>abs(B) sinp_sig =array([A*sin(w*t) if abs(A*sin(w*t))<B else A*sin(w*t)*B/abs(A*sin(w*t)) for t in range(N)]) plt.plot(arange(N)/float(FD), sinp_sig, 'r')# plt.xlabel(', .') plt.ylabel(' ') plt.title(' c ') plt.grid(True) plt.show() spectr_sinp = rfft(sinp_sig ) plt.plot(rfftfreq(N, 1./FD), np_abs(spectr_sinp)/N)# plt.xlabel(', ') plt.ylabel(' ') plt.title(' ') plt.grid(True) plt.show()
制限記号Bを考慮するために、次のコードが使用されました-A * sin(w * t)* B / abs(A * sin(w * t)。
振幅がゼロに遷移する信号の形式と非線形要素のスペクトルを取得します。
# «c » A*sin(w*t) abs()=abs(B) sinn_sig = array([A*sin(w*t) if abs(A*sin(w*t))<B else 0 for t in range(N)]) plt.plot(arange(N)/float(FD), sinn_sig, 'r') plt.xlabel(', .') plt.ylabel(' ') plt.title(' c ') plt.grid(True) plt.show() spectr_sinn = rfft(sinn_sig ) plt.plot(rfftfreq(N, 1./FD), np_abs(spectr_sinn)/N)# plt.xlabel(', ') plt.ylabel(' ') plt.title(' ') plt.grid(True) plt.show()
結果
非線形要素の入力および出力での信号。

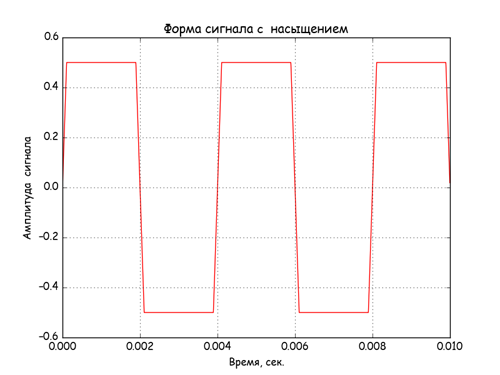
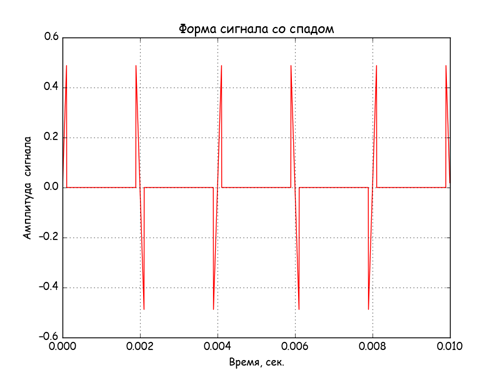
非線形要素の出力での信号のスペクトル。


減衰信号を持つ非線形要素は、多数の高周波高調波を生成します。 非線形要素の出力で信号をフィルター処理するには、[3]で詳細に説明されているデジタルローパスフィルターを適用できます。 プログラムコード[3]の非線形要素の信号のデジタルフィルタリングの可能性を調べるために、次の変更が行われました。
A=1.0 B=0.4 test_n = 2560 # - test_f = 200 # test_period_count = 10.0 # - test_t = numpy.linspace(0.0, test_period_count/test_f, test_n) # sin(wt), test_base_signal = array([A*sin(2*pi*test_f* i) for i in test_t ]) test_signal =array([A*sin(2*pi*test_f* i) if abs(sin(2*pi*test_f* i))<B else 0 for i in test_t ]) #test_signal=array([A*sin(2*pi*test_f* i) if abs(A*sin(2*pi*test_f* i))<B else A*sin(2*pi*test_f* i)*B/abs(A*sin(2*pi*test_f* i)) for i in test_t ])
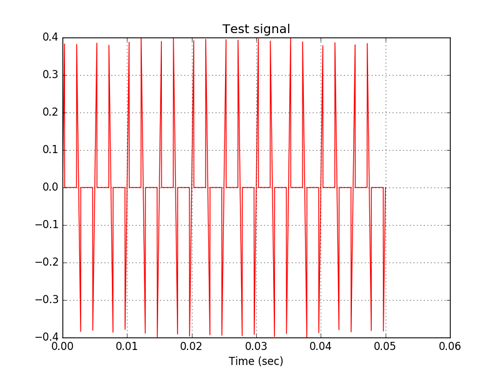

フィルターの出力での信号のスペクトル。
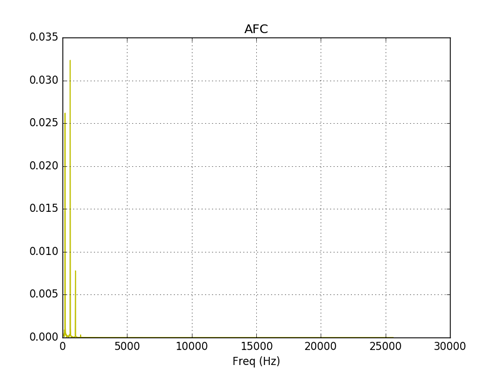
おわりに
マイクロプロセッサを使用してハードウェアで非線形要素を使用する問題を解決することは可能ですが、DACとADCだけでなく信号レベルも一致させる必要があります。
参照資料
1. Python調和線形化法
2. 高調波線形化の方法
3. デジタルフィルター