🤳🏽 🖐🏼 🤘🏻 機械学習のジオメトリ。超平面の分離、または線形結合の幾何学的な意味は何ですか？ 💷 🚾 🖐🏽

ニューラルネットワークを含む多くの機械学習アルゴリズムでは、加重和、またはそうでなければ入力ベクトル成分の線形結合を常に処理する必要があります。そして、結果のスカラー値の意味は何ですか？

記事では、すべての例を簡単に再現し、独自の実験を行うことができるように、多くの図とPythonコードだけでなく、例、式、この質問に答えようとします。

モデル例

理論が実際のケースから外れないように、例としてバイナリ分類問題を取り上げます。データセットがあります：m個のサンプル、各サンプルはn次元の点です。各サンプルについて、それが属するクラス（緑または赤）がわかります。データセットが線形に分離可能であることも知られています。緑のドットがその片側にあり、赤のドットがもう一方の側にあるようなn次元の超平面があります。

このような超平面を見つける問題の解決策は、たとえばロジスティック回帰（ロジスティック回帰）、線形カーネルを使用したサポートベクトルの方法（線形SVM）、または最も単純なニューラルネットワークを使用するなど、さまざまな方法でアプローチできます。

記事の最後で、パーセプトロン学習メカニズムをゼロから記述し、得られた知識を使用して、バイナリ分類問題を自分の手で解決します。

直線から超平面へ

直線の詳細な計算を検討してください。 n次元空間の超平面の一般的な場合、すべてがまったく同じであり、ベクトルの成分の数に合わせて調整されます。

平面上の直線は3つの数字で定義されます-

（ w_{1} 、 w_{2} 、 b ）

$（w_1、w_2、b）$ ：

w_{1} x_{1} + w_{2} x_{2} + b = 0

$w_1 x_1 + w_2 x_2 + b = 0$

または：

s u m_{i = 1}^{2} w_{i} x_{i} + b = 0

$\ sum_ {i = 1} ^ {2} {w_ix_i} + b = 0$

または：

w^{T} x + b = 0

$w ^ Tx + b = 0$

最初の2つの要因

w_{1} 、 w_{2}

$w_1、w_2$ ポイント（0、0）を通る直線のファミリー全体を定義します。の関係

w_{1}

$w_1$ そして

w_{2}

$w_2$ 軸に対する線の傾斜角度を決定します。

もし

w_{1} = w_{2}

$w_1 = w_2$ 、45度の角度で走るラインを取得します（

f r a c p i 4

$\ frac {\ pi} {4}$ ）軸へ

x_{1}

$x_1$ そして

x_{2}

$x_2$ そして、第1/3象限を半分に分割します。

非ゼロ係数

b

$b$ 行がゼロを通過しないようにします。この場合、軸への傾き

x_{1}

$x_1$ そして

x_{2}

$x_2$ 変わりません。つまり

b

$b$ 平行線のファミリーを定義します：

ベクトルの幾何学的な意味。

（ w 1 、 w 2 ）

$（w1、w2）$ 直線に垂直

w_{1} x_{1} + w_{2} x_{2} + b = 0

$w_1 x_1 + w_2 x_2 + b = 0$ ：

（オフセットを考慮しない場合

b

$b$ それから

w^{T} x

$w ^ Tx$ 2つのベクトルのスカラー積にすぎません。ゼロへの平等は、それらの直交性と同等です。だから

x

$x$ -直交ベクトルのファミリー

（ w_{1} 、 w_{2} ）

$（w_1、w_2）$ ）

PS線を定義するトリプル（w1、w2、b）など、無限に多くのそのような法線があることは明らかです。 3つの数値すべてに非ゼロ係数が乗算された場合

k

$k$ -行は同じままです。

n次元空間の一般的な場合、

（ w_{1} 、 . . . 、 w_{n} 、 b ）

$（w_1、...、w_n、b）$ n次元の超平面を定義します。

w_{1} x_{1} + w_{2} x_{2} + . . . + w_{n} x_{n} + b = 0

$w_1 x_1 + w_2 x_2 + ... + w_n x_n + b = 0$

または：

s u m_{i = 1}^{n} w_{i} x_{i} + b = 0

$\ sum_ {i = 1} ^ {n} {w_ix_i} + b = 0$

または：

w^{T} x + b = 0

$w ^ Tx + b = 0$

線形結合の幾何学的な意味

ポイントが

x （ x_{0} 、 . . . 、 x_{n} ）

$x（x_0、...、x_n）$ その後、超平面上にあります

w^{T} x + b = 0

$w ^ Tx + b = 0$

ポイントが平面上にない場合、この合計はどうなりますか？

ハイパープレーンは、ハイパースペースを2つのハイパースペースに分割します。そのため、これらのサブスペースの1つ（条件付きで「超平面」の上にある）にあるポイントと、これらのサブスペースのもう1つにあるポイント（条件付きで「超平面」の下にある）は、この合計で異なる符号を与えます：

w^{T} x + b > 0

$w ^ T x + b> 0$ -ポイントは超平面の「上」にあります

w^{T} x + b < 0

$w ^ T x + b <0$ -ポイントは超平面の「下」にあります

これは非常に重要な観察であるため、単純なPythonコードで再確認することをお勧めします。

Pythonサンプルコード

#   #  ,        import seaborn import matplotlib.pyplot as plt import numpy as np #  : w1 * x1 + w2 * x2 + b = 0 def line(x1, x2): return -3 * x1 - 5 * x2 - 2 #     x2 = f(x1) ( ) def line_x1(x1): return (-3 * x1 - 2) / 5 #    np.random.seed(0) x1x2 = np.random.randn(200, 2) * 2 #   for x1, x2 in x1x2: value = line(x1, x2) if (value == 0): #  —   plt.plot(x1, x2, 'ro', color='blue') elif (value > 0): #  —   plt.plot(x1, x2, 'ro', color='green') elif (value < 0): #  —   plt.plot(x1, x2, 'ro', color='red') #       plt.gca().set_aspect('equal', adjustable='box') #    x1_range = np.arange(-5.0, 5.0, 0.5) plt.plot(x1_range, line_x1(x1_range), color='blue') #    plt.xlabel('x1') plt.ylabel('x2') #  ! plt.show()

「上」と「下」は条件付きの概念であることを理解する必要があります。これは例に具体的に反映されています-緑のドットは視覚的に低くなっています。幾何学的な観点から、この特定の線の「上」の方向は法線ベクトルによって決まります。法線が見えるところには、上部があります：

T.O. 線形結合記号を使用すると、ポイントを上部または下部のサブスペースに割り当てることができます。

そしてその意味は？値（モジュロ）は、平面からの点の距離を決定します。

d i s t （ x ） = f r a c | w^{T} x + b | | | w | |

$dist（x）= \ frac {| w ^ Tx + b |} {|| w ||}$

つまりポイントが平面から遠いほど、その線形結合の値は大きくなります。線形結合の値を修正すると、元の線に平行な線上にある点が得られます。

繰り返しますが、観察は重要なので、再確認します。

Pythonサンプルコード

 #   #   #  ,        import seaborn import matplotlib.pyplot as plt import numpy as np #  : w1 * x1 + w2 * x2 + b = 0 def line(x1, x2): return -3 * x1 - 5 * x2 - 2 #     x2 = f(x1) ( ) def line_x1(x1): return (-3 * x1 - 2) / 5 #    np.random.seed(0) x1x2 = np.random.randn(200, 2) * 2 #   for x1, x2 in x1x2: value = line(x1, x2) #   ,    —   #  —     [0, 0.75] #  (0) —   , - (0.75) —   color = str(max(0, 0.75 - np.abs(value) / 30)) plt.plot(x1, x2, 'ro', color=color) #       plt.gca().set_aspect('equal', adjustable='box') #    x1_range = np.arange(-5.0, 5.0, 0.5) plt.plot(x1_range, line_x1(x1_range), color='blue') #    plt.xlabel('x1') plt.ylabel('x2') #  ! plt.show()

それはすべて一緒に収まります。

結論

線形結合により、n次元空間を超平面で分割できます。
超平面の反対側の点は、線形結合の異なる符号を持ちます $w ^ Tx + b$ 。
超平面から離れるほど、線形結合の絶対値が大きくなります。

バイナリ分類の観点から、最後のステートメントは次のように再定式化できます。ポイントが決定平面である超平面から遠ければ遠いほど、このポイントによって定義されたサンプルが1つまたは別のクラスに分類されることを確信できます。

近いところと遠いところ：どうですか？

概念は非常に主観的です。そして、分類では明確に答える必要があります-火星に飛ぶロケットの建設に適しているか、これは結婚です。ユーザーが広告をクリックするかどうか。ある程度の自信を持って答えることができます-肯定的な（真の）結果の確率を与えるために。

これを行うには、活性化関数を線形結合に適用できます（ニューラルネットワークの用語で）。

ロジスティック関数を適用する場合（下の図を参照）：

ロ ジ ス テ ィ ッ ク （ x ） = f r a c 1 1 + e^{- x}

$ロジスティック（x）= \ frac {1} {1 + e ^ {-x}}$

確率の出力とそのような画像を取得します。

Pythonサンプルコード

 #   #  ,        import seaborn import matplotlib.pyplot as plt import numpy as np #   def logit(x): return 1 / (1 + np.exp(-x)) #  : w1 * x1 + w2 * x2 + b = 0 def line(x1, x2): return 3 * x1 + 5 * x2 + 2 #     x2 = f(x1) ( ) def line_x1(x1): return (-3 * x1 - 2) / 5 #    np.random.seed(0) xy = np.random.randn(200, 2) * 2 #   for x1, x2 in x1x2: #     —    value = logit(line(x1, x2) / 2) if (value < 0.001): color = 'red' elif (value > 0.999): color = 'green' else: color = str(0.75 - value * 0.5) plt.plot(x1, x2, 'ro', color=color) #       plt.gca().set_aspect('equal', adjustable='box') #    x1_range = np.arange(-5.0, 5.0, 0.5) plt.plot(x1_range, line_x1(x1_range), color='blue') #    plt.xlabel('x1') plt.ylabel('x2') #  ! plt.show()

レッズ-間違いではありません（偽、結婚のように、クリックしません）。緑-まさにはい（本当、ちょうどいい、クリックします）。超平面（解の境界）に特定の近接範囲内にあるすべてのものは、何らかの確率を取得します。最も直接的な確率では、正確に0.5です。

PSここで「正確に」は、0.001未満または0.999を超えると定義されます。ロジスティック関数自体は、負の無限大でゼロになり、正の無限大で団結する傾向がありますが、これらの値を取りません。

注：この例は、符号付き距離を確率間隔に押し込む方法のみを示していることに注意してください。

（ 0 、 1 ）

$（0、1）$ 。実際の問題では、最適なマッピングを見つけるために確率キャリブレーションが使用されます。たとえば、Plattスケーリングアルゴリズムでは、ロジスティック関数がパラメーター化されます。

f （ x ） = f r a c 1 1 + e^{A x + B}

$f（x）= \ frac {1} {1 + e ^ {Ax + B}}$

そしてオッズ

A

$A$ そして

B

$B$ 機械学習により選択。詳細については、バイナリ分類子キャリブレーション、確率キャリブレーションを参照してください。

私たちはどのスペースにいますか？（有用な投機的演習）

それは明らかなようです-私たちはデータスペースにいます

X

$X$ （データ空間）サンプルが存在する場所

x

$x$ 。そして、ベクトルで定義される平面による最適な分離を探しています

w

$w$ 。

w^{T} x + b > 0

$w ^ T x + b> 0$ 緑のドット用

w^{T} x + b < 0

$w ^ T x + b <0$ 赤い点用

しかし、バイナリ分類の問題では、サンプルが固定され、重みが変化します。したがって、重みの空間に入ることですべてを再生できます

W

$W$ （重量スペース）：

x^{T} w + b

$x ^ T w + b$

トレーニングセットのサンプル

x_{1} . . . x_{m}

$x_1 ... x_m$ この場合セット

m

$m$ 超平面と私たちのタスクは、そのような点を見つけることです

w

$w$ 、各平面の右側にあります。ソースデータセットが線形分離可能である場合、そのようなポイントが存在します。

Pythonサンプルコード

 #   #  ,        import seaborn import matplotlib.pyplot as plt import numpy as np #  1 def line1(w1, w2): return -3 * w1 - 5 * w2 - 8 #     w2 = f1(w1) ( ) def line1_w1(w1): return (-3 * w1 - 8) / 5 #  2 def line2(w1, w2): return 2 * w1 - 3 * w2 + 4 #     w2 = f2(w1) ( ) def line2_w1(w1): return (2 * w1 + 4) / 3 #  3 def line3(w1, w2): return 1.2 * w1 - 3 * w2 + 4 #     w2 = f2(w1) ( ) def line3_w1(w1): return (1.2 * w1 + 4) / 3 #  4 def line4(w1, w2): return -5 * w1 - 5 * w2 - 8 #     w2 = f2(w1) ( ) def line4_w1(w1): return (-5 * w1 - 8) / 5 #    w1_range = np.arange(-5.0, 5.0, 0.5) w2_range = np.arange(-5.0, 5.0, 0.5) #   (w1, w2),       for w1 in w1_range: for w2 in w2_range: value1 = line1(w1, w2) value2 = line2(w1, w2) value3 = line3(w1, w2) value4 = line4(w1, w2) if (value1 < 0 and value2 > 0 and value3 > 0 and value4 < 0): color = 'green' else: color = 'pink' plt.plot(w1, w2, 'ro', color=color) #       plt.gca().set_aspect('equal', adjustable='box') #    ()   1 plt.plot(w1_range, line1_w1(w1_range), color='blue') #   2 plt.plot(w1_range, line2_w1(w1_range), color='blue') #   3 plt.plot(w1_range, line3_w1(w1_range), color='blue') #   4 plt.plot(w1_range, line4_w1(w1_range), color='blue') #     —    plt.axis([-7, 7, -7, 7]) #    plt.xlabel('w1') plt.ylabel('w2') #  ! plt.show()

モデルを訓練するとき、重みの空間で推論する方が便利です。重みが更新され、トレーニングセットのサンプルベクトルが超平面の法線を定義します。例：

サンプルと仮定します

x

$x$ 不等式に対応する緑のクラスに対応します。

x^{T} w + b > 0

$x ^ T w + b> 0$

なぜならベクトル図

w

$w$ 普通に見える

x

$x$ 、線形結合の値は負になります-したがって、分類エラーがあります。

したがって、ベクトルを更新する必要があります

w

$w$ 法線で示される側へ：

w_{n e w} = w_{o l d} + l a m b d a x

$w_ {new} = w_ {old} + \ lambda x$ どこで

l a m b d a > 0

$\ lambda> 0$

いくらかの「速度」で

\ラ ム ダ

$\ラムダ$ 。したがって、次のステップでは、予測は真であるか偽であるかのどちらかです。期間

\ラ ム ダ x

$\ラムダx$ 、法線に合わせて、重みベクトルを緑の領域に「プル」します。

練習。パーセプトロンを訓練する

サンプルの線形分離性の場合のバイナリ分類の問題を解決するために、このスキームに従って配置された単純なパーセプトロンをトレーニングできます。

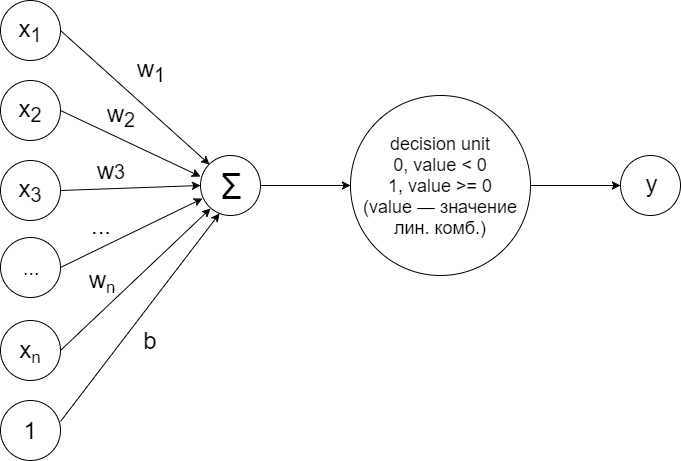
この設計は、上記で説明した原則を正確に実装しています。線形結合が計算されます：

s u m_{i = 1}^{n} w_{i} x_{i} + b

$\ sum_ {i = 1} ^ {n} {w_ix_i} + b$

ソルバー（決定単位）が、次の原則に従って2つのクラスのいずれかにサンプルを帰属させることを決定する値によって：

w^{T} x + b g e 0

$w ^ T x + b \ ge 0$ クラス+1（緑色の点）

w^{T} x + b < 0

$w ^ T x + b <0$ クラス-1（赤い点）

最初に、重みはランダムに初期化され、各サンプルの各トレーニングステップで次のアルゴリズムが実行されます。

予測ラベルが計算されます。実際のクラスと一致しない場合、次の原則に従って重みが更新されます。

w_{n e w} = w_{o l d} + y_{n} x_{n} b_{n e w} = b_{o l d} + y_{n}

$w_ {new} = w_ {old} + y_nx_n \\ b_ {new} = b_ {old} + y_n$

どこで

y_{n}

$y_n$ -サンプルの実際のクラス

x_{n}

$x_n$ 。なぜこれが機能するのかは、重みの空間への移行を伴う投機的な演習で上で説明されています。簡単に：

重みベクトルを正しいクラスに向けて回転させます：normal $x_n$ クラス+1の場合。通常に対して $x_n$ クラス-1の場合。（法線自体は常にクラス+1の方向を向いています。）
同様の原則に従ってオフセットを更新します。

結果は次のとおりです。

Pythonコード

 #   #  ,        import seaborn #   import matplotlib.pyplot as plt import numpy as np #  —   np.random.seed(17) #     x1x2_green = np.random.randn(200, 2) * 2 + 21 #     x1x2_red = np.random.randn(200, 2) * 4 + 5 #      x1x2 = np.concatenate((x1x2_green, x1x2_red)) #  :  +1,  -1 labels = np.concatenate((np.ones(x1x2_green.shape[0]), -np.ones(x1x2_red.shape[0]))) #   indices = np.array(range(x1x2.shape[0])) np.random.shuffle(indices) x1x2 = x1x2[indices] labels = labels[indices] #    w1_ = -1.1 w2_ = 0.5 b_ = -20 #   ( ) def lr_line(x1, x2): return w1_ * x1 + w2_ * x2 + b_ #   -1 #  +1 def decision_unit(value): return -1 if value < 0 else 1 #      lines = [[w1_, w2_, b_]] for max_iter in range(100): #     #    mismatch_count = 0 #    for i, (x1, x2) in enumerate(x1x2): #       value = lr_line(x1, x2) #     (-1, +1) true_label = int(labels[i]) #   (-1, +1) pred_label = decision_unit(value) #      if (true_label != pred_label): #      , .. #    — (x1, x2) —    +1 #    — (-x1, -x2) —    -1 # ..      +1 w1_ = w1_ + x1 * true_label w2_ = w2_ + x2 * true_label #      b_ = b_ + true_label #      mismatch_count = mismatch_count + 1 #       if (mismatch_count > 0): #    lines.append([w1_, w2_, b_]) else: #  —   break #   (   ) for i, (x1, x2) in enumerate(x1x2): pred_label = decision_unit(lr_line(x1, x2)) if (pred_label < 0): plt.plot(x1, x2, 'ro', color='red') else: plt.plot(x1, x2, 'ro', color='green') #       plt.gca().set_aspect('equal', adjustable='box') #    plt.xlabel('x1') plt.ylabel('x2') #       x1_range = np.arange(-30, 50, 0.1) # ,         # x2 = f(x1) = -(w1 * x1 + b) / w2 def f_lr_line(w1, w2, b): def lr_line(x1): return -(w1 * x1 + b) / w2 return lr_line #      it = 0 for coeff in lines: lr_line = f_lr_line(coeff[0], coeff[1], coeff[2]) plt.plot(x1_range, lr_line(x1_range), label = 'it: ' + str(it)) it = it + 1 #  plt.axis([-15, 30, -15, 30]) #  plt.legend(loc = 'lower left') #  ! plt.show()

重みの空間を見てみましょう

$W$ （重量スペース）：

Pythonコード

 # NB     .      . #     w1_range = np.arange(0, 10, 0.1) for i, (x1, x2) in enumerate(x1x2): if (labels[i] == 1): color = 'green' else: color = 'red' #  x1 * w1 + x2 * w2 + b = 0 #   w2 = f(w1) # ( ) def line(w1): return -(x1 * w1 + b_) / x2 #  ;    —   plt.plot(w1_range, line(w1_range), color = color) #   ,     plt.plot(w1_, w2_, 'ro', color='blue') #  plt.axis([0, 10, 0, 10]) #       plt.gca().set_aspect('equal', adjustable='box') #    plt.xlabel('w1') plt.ylabel('w2') #  ! plt.show()

赤と緑の線はソースサンプル、青の点は総重量です。

そして、他のどの重みが正しい分類を与えますか？私たちは見ます：

Pythonコード

 # NB     .      . #     w1_range = np.arange(0, 10, 0.5) w2_range = np.arange(0, 10, 0.5) #  ,    for i, (x1, x2) in enumerate(x1x2): def line(w1): return -(x1 * w1 + b_) / x2 if (labels[i] == 1): color = 'green' else: color = 'red' plt.plot(x1_range, line(x1_range), color = color) #    (),      plt.plot(w1_, w2_, 'ro', color='blue') #   def f(w1, w2, x1, x2): value = x1 * w1 + x2 * w2 + b_ return -1 if value < 0 else 1 #     (  ) #        (data space) good_weights = [] #    ,         #      for w1 in w1_range: for w2 in w2_range: in_range = True for i, (x1, x2) in enumerate(x1x2): if (labels[i] != f(w1, w2, x1, x2)): in_range = False break if (in_range): good_weights.append([w1, w2, b_]) #     () plt.plot(w1, w2, 'ro', color = 'magenta') #  plt.axis([0, 10, 0, 10]) #       plt.gca().set_aspect('equal', adjustable='box') #    plt.xlabel('w1') plt.ylabel('w2') #  ! plt.show() #   ( ) def lr_line(x1, x2): return w1_ * x1 + w2_ * x2 + b_ #   -1 #  +1 def decision_unit(value): return -1 if value < 0 else 1 #   (   ) for i, (x1, x2) in enumerate(x1x2): pred_label = decision_unit(lr_line(x1, x2)) if (pred_label < 0): plt.plot(x1, x2, 'ro', color='red') else: plt.plot(x1, x2, 'ro', color='green') #       x1_range = np.arange(-30, 50, 0.1) for (w1, w2, _b) in good_weights: #    ,  x1, x2 —  def w_line(x1): return -(w1 * x1 + b_) / w2 #      plt.plot(x1_range, w_line(x1_range)) #  plt.axis([0, 25, 0, 25]) #       plt.gca().set_aspect('equal', adjustable='box') #    plt.xlabel('x1') plt.ylabel('x2') #  ! plt.show()

赤と緑の線はソースサンプル、青の点は総重量、紫の点は他の可能な重量です。

そして、すべてを再び裏返し、再びデータ空間に変えます

X

$X$ （データスペース）：

上の図の重み空間、ここではデータ空間で紫色の点でマークされた重みは、ソリューションの他の可能な境界の線になりました。

演習（単純）：最後の図では、4つの特徴的な線の束。スケールのスペースにある紫色のドットの中から見つけてください。

著者から

記事の最初のバージョンに関する重要なコメントを寄せてくれたすべてのKhabrovsk市民に感謝します。yorkoは、 Open Data Scienceコミュニティとともに、超クールなオープンマシンラーニングコースを実施しています。皆さんにお勧めします。

資料には最終的な仕上げがなく、記事は改訂のために送られたことが明らかになりました。 2番目の（現在の）バージョンには、パーセプトロントレーニングの例が追加されています。

まとめ

この記事が、線形結合の幾何学的な意味をより良く理解し、感じることを願っています。以下は、記事の準備に使用される資料へのリンクであり、トピックを深めるという点で興味深いものです。（すべての資料は英語です。）

ジェフリーヒントン。ニューラルネットワークアーキテクチャの主なタイプの概要

ニューラルネットワークの第一人者Jeffrey Hintonから重み空間への移行でパーセプトロンをトレーニングする方法の詳細をお読みください。
教師あり学習/サポートベクターマシン

サポートベクトル法によるバイナリ分類問題の解決と、このアルゴリズムの観点から最適な分割面を選択する方法について。
超平面ベースの分類：パーセプトロンおよび（はじめに）サポートベクターマシン

パーセプトロンについても、サポートベクターの方法についてはさりげなく。トレーニングとウェイト調整の問題を詳細に調べます。
多面体と線形計画法。多面体、多面体、および円錐

多くの実例となる線形結合（理論）の線形代数。

機械学習のジオメトリ。 超平面の分離、または線形結合の幾何学的な意味は何ですか？

モデル例

直線から超平面へ

線形結合の幾何学的な意味

結論

近いところと遠いところ：どうですか？

私たちはどのスペースにいますか？ （有用な投機的演習）

練習。 パーセプトロンを訓練する

著者から

まとめ

More articles:

機械学習のジオメトリ。超平面の分離、または線形結合の幾何学的な意味は何ですか？

私たちはどのスペースにいますか？（有用な投機的演習）

練習。パーセプトロンを訓練する