ゆう ビチコフ、S.V。 シチェルバコフ
ヤコビ関数行列の固有値を使用した非線形非自律システムの数学モデルのダイナミクスの定性的特徴の研究
問題の声明
集中定数を持つ非線形非自律システムの数学モデルのダイナミクスの定性的特徴を研究するタスクは非常に緊急です。 非線形現象の理論と得られた応用結果の開発は、この問題を解決するためのさまざまな方法を生み出します[1-3]。
一般的な場合、識別されたクラスのシステム(以下「システム」)の数学的モデルのダイナミクスは、非定常係数を持つ次の通常の非線形積分微分方程式によって記述されます。
A(D)x(t)=G(D)f(t)+H(x、f、t) qquad(1)
どこで D 独立変数に関する一般化微分の演算子 t ; A(D) -正方形、順序 Lx 多項式を含む行列 D そして D−1 要素 D−1 -上限が可変の積分演算子 t ;
G(D)はサイズの長方形行列です L x timesL f からの多項式 D そして D−1 要素; x(t) そして f(t) -システム座標のマトリックス列(求められている解決策)およびそれぞれに対する外部の影響。 H(x、f、t) -因子が非定常係数である積の和の形式の行を含む列行列、および任意の小数の有理度で、ゼロから始まる、任意の解および外部の影響からの任意の次数および任意の多重度の積分の古典的な微分
与えられた初期条件下での非線形非自律システムのダイナミクスの計算 Dnx r(0−)=Dnx r(t −0) 、 r=1,2、...、L x 、 0−=t− 0 、 n in[0;M−1] 与えられた学習間隔内に存在するすべてを見つけることになります [t 0;T] 方程式(1)の解であり、多くのアルゴリズムおよび数学の問題に関連しています。 これらの問題の本質は、目的とする解決策の質的特徴の客観的な多様性を決定します。
一般的な場合、式(1)の求められている解のダイナミクスの性質は予測不能です。これは、選択された初期条件、パラメーターの比率、およびその特性のタイプに対する、システムの支配的な非線形および非定常特性の発現形式の依存性によるものです。 一般的な場合、方程式の求められた解のインデックス (1) 不規則で、システムのダイナミクスをいわゆる決定論的カオスに低下させます[2-4]。 そのダイナミクスを特徴付ける、我々は方程式の望ましい解決策で (1) 微分可能なものを含む第1種のブレーク、および第2種のブレークが可能です。 これらのソリューションの特異性は、通常「剛性」に関連付けられていることです。 動的インジケータの間隔を高速と低速で交互に変更し、その間隔内で、局所安定性から不安定性へ、またはその逆への移行が可能です。 局所的な不安定性の直接的な結果は、解の「混合」であり、非線形非自律システムのダイナミクスを数値的に計算し、その定性的特徴を分析するタスクを非常に複雑にします[5]。 非線形非自律システムのダイナミクスの可能性のある定性的多様性は、その座標パラメトリック関係の多音節織りの結果であり、方程式の近似解のみを可能にします (1) いずれかの数値的方法を使用する[6-8]。 多くの数値的方法があり、それらの設計スキームは常に改善されています。 ただし、それらのいずれも、方程式の望ましい解の振る舞いの性質間の関係またはパターンを閉じた形で確立することはできません (1) この方程式の情報インジケータ。 このような関係を区別し、それに基づいて方程式の定性的特徴と特性の特性の分析を整理するタスク (1) 理論的にも応用的にも重要です。 彼女の決定は、非線形および非定常現象における因果関係の内容を理解するための別のステップを意味します。
この記事では、情報指標としてのダイナミクス方程式に対応する非線形非自律固有値システムのダイナミクスの使用に基づく問題の解決策を提供します (1) この方程式の解の固有値による関数ヤコビ行列と分解。 計算の基礎として、解析的数値法が使用されました。これは、その計算特性においてタスクに対応します[9、10]。 実例が提供されます。
非線形非自律システムのダイナミクスの情報インジケーターの分離
求められた方程式の解の定性的特徴の情報指標の構成 (1) この方程式のパラメーターと解自体の非定常インジケーターの相互作用を決定するものを含めることをお勧めします。 線形定常システムでは、そのダイナミクスは方程式によって記述されます (1) で H(x、f、t)=const 、そのような情報インジケータはルーツです lambda n、n=1,2、...、N 次の特性方程式:
A(p)=0 qquad(2)
どこで A(p) -行列式 A(D) 演算子を置き換えるとき D オペレーターごと p 。
方程式の根の性質と数値 (2) 、安定性と「剛性」を含む、移行プロセスにおける線形自律システムのダイナミクスのすべての機能と特性を決定します[1,7,8]。 外部の影響が定常状態の性質を明確に支配するため、線形自律システムのダイナミクスは、半無限の時間間隔で完全に予測可能です。
非線形の非自律システムのダイナミクスの指標を決定する際に、このような情報集約的でかなり単純な指示された選択はまだ不可能です。 しかし、現在の緊急の実践要求では、計算にアクセス可能であり、情報内容の観点から許容可能なシステムの指標を選択する必要があります。 線形の場合と同じように進むと、必要な情報インジケータとしてルートを考慮するという提案は論理的です lambda n、n=1,2、...、N 方程式 (2) 、その形成は行列式の計算に関連付けられます A(p) 行列 A(D) 方程式の選択された線形部分 (1) 。 結果の情報インジケーターのセマンティックコンテンツの解釈 lambda n、n=1,2、...、N これらの選択された本質的に静止しているインジケータと非線形非自律システムのダイナミクスの定性的特徴との関係は、段階的であっても意味のある識別には役立たないため、あいまいです。 また、方程式 (1) 行列 A(D) ゼロまたは非線形部分により強調表示 H(x、f、t) この方程式の次に、方程式の根 (2) 一般的に不在またはその存在、したがってコンテンツは、本質的に条件付きで主観的です[9]。
したがって、非線形非自律システムのダイナミクスの許容可能な情報インジケータの選択の目標兆候は、その存在の条件であり、方程式の望ましい解の数値インジケータとの数学的関係です (1) 。 この条件は、等式の場合に満たすことができます (1) 線形部分行列 A(D) 特定の方法で、マトリックスによるハイライトまたは補足 H(x、f、t) 非線形部分[9,10]。 そのようなマトリックスの選択または追加 A(D) マトリックスのため H(x、f、t) おそらくあいまいな方法で。 この場合に実行される変換はすべて同等の性質である必要があり、その結果、システムのダイナミクスは変更されません。 マトリックスの選択または追加の結果として A(D) マトリックスのため H(x、f、t) 根の必要な数学的関係が達成されます lambda n、n=1,2、...、N 方程式 (2) 方程式の望ましい解の数値 (1) システムダイナミクスの数値計算のステップによって決定される離散的な瞬間。 したがって、方程式のこれらの変換の結果として (1) ルーツ lambda n、n=1,2、...、N 方程式 (2) 数値指標と定性的特性の両方に関して、時間に依存する機能を獲得します。
非定常ルートプロパティ lambda n、n=1,2、...、N 方程式 (2) 、対応する行列変換を実行するためのターゲット基準がない場合 A(D) 、そのような特性の出現につながる、これらのルートの必要な有益な特性をそれ自体で保証することはできません。 非線形オブジェクトのダイナミクスの定性的特徴の望ましい研究は、形成または変換のターゲット基準として既存のマトリックスを選択することにより決定されます A(D) 方程式 (1) この方程式に対応するヤコビ関数行列との一致の条件[4-8]。 このような問題を解決するためのアルゴリズムは、[10]で説明されています。 マトリックスの形成または変換の結果として A(D) マトリックスのため H(x、f、t) 関数ヤコビ行列の非定常根 lambda n、n=1,2、...、N 方程式 (2) ヤコビ行列の固有値の状態を取得します。
非定常固有値 lambda n、n=1,2、...、N 関数ヤコビ行列方程式 (1) 数値解法のステップによって決定される離散的な瞬間には、特定のセマンティックコンテンツがあります[4-8]。 非線形非自律システムのダイナミクスの局所特性であるため、離散時間モーメントtに対応する点の無限に小さな近傍で、ダイナミクス方程式の解のダイナミックインジケータの安定性と変化率を特徴付けます (1) 。 方程式の特異点の近傍 (1) 固有値 lambda n、n=1,2、...、N 関数ヤコビ行列により、位相平面上で位相軌道の引力と反発の領域を区別することができ、この方程式の既存の解の限界状態に関する予測が可能になります[6-8]。 離散時刻に対応する固有値 lambda n、n=1,2、...、N 非線形非自律システムのダイナミクスの定性的特徴と特性を特徴付け、決定するヤコビ関数行列は、この関係の数学的特徴と情報指標を識別するタスクの関連性を決定します。 この問題の解決策は、選択された非定常情報インジケータ間の数学的関係の確立に関連しています lambda n、n=1,2、...、N 非線形非自律システムのダイナミクスと、このダイナミクスの計算に使用される数値法の計算スキームのパラメーター。 この目標を達成するために必要な条件は、対応する分析部品の選択されたメソッドの設計スキームに存在することです。 メソッドのこの分析部分の計算アルゴリズムは、ヤコビ関数行列の固有値を計算する機能と一致している必要があり、これらの数値と非線形非自律システムの動的座標との数学的関係も提供する必要があります。 定式化された要件は、可変次数のワンステップ分析数値法によって完全に満たされます[9、10]。
非線形非自律システムのダイナミクスを計算するための解析的数値的方法
解析的数値的手法の形成への動機は、方程式の解を統一したいという願望でした (1) 同一の変換のみを使用します。 これは、テイラー級数による望ましい解の記述と、提起された問題の代数化のためのラプラス積分のその後の適用を意味します。
方程式によって選択されたダイナミクスを計算するための解析的数値的方法 (1) 指定された学習間隔内のシステムのクラス [t 0;T] 分析と数値の2つの部分で構成されます。
このメソッドの分析部分は、一般化された関数、ラプラス変換、および関数のべき級数の装置に基づいています。 分析部分の手順は、後続の各計算ステップの実行に先行し、次のようになります。 まず、対応するべき級数のシステムの外部の影響と非定常パラメーターを記述する関数を拡張するとともに、マトリックスにあるそれらのソリューションの通常のコンポーネントを正式に記述することにより、 H(x、f、t) 方程式 (1) 対応するべき級数を使用して、この方程式の右辺を列行列に変換します。この行列のべき要素は行要素として機能します。 これらのべき級数の係数は、システムの外部の影響と非定常パラメーターのべき級数の既知の係数、および求められるいくつかの解の正規成分のべき級数の未知の係数で表されるため、一般に不明です。 実行された操作は元の方程式を導きます (1) ラプラス積分変換のその後のアプリケーションに必要な形式に。 修正された方程式を変換するラプラス (1) そして、Cramerのルールに従って、結果の代数方程式を画像に対して解きます X l(p) 求められた解決策 x l(t)、l in[1、L x] 次の式を取得します。
X l(p)= fracBl l(p)A(p)= frac sum limits i=0inftyBl l.N+J l−ipN+J l−i sum limits Ni=0A ipi、 qquad(3)
どこで N in mathbbN;J l in mathbbZ
一般的な場合、式(3)で表される分数有理関数 J l geq0 間違っており、合理的な全体の合計として表すことができます X −l(p) 正しい分数の有理数 X +l(p) 機能。 正しい分数有理関数のその後の分解 X +l(p) 無限遠点の近傍にあるローラン級数では、式を変換します (3) 次のように:
X l(p)=X −l(p)+X +l(p)= sum −J lj=0S ljp−j+ frac sum limits inftyi=1B lN−ipNi sum limits Ni=0A ipi== sum −J lj=0S ljp−j+ frac sum limits inftyi=0B l.N−i−1pN−i sum limits Ni=0A ipi frac1p== sum −J lj=0S l.jp−j+ sum inftyi=0R l.ip−(i+1)。 qquad(4)
オッズ S l.j 、 B l.N−i 、 R l.i 式に含まれる (4) 、式の表記を考慮して (3) 、次の式[9,10]で計算されます。
S l。−J l= fracBl l.N+J lA N;
S l。−J l+j= fracBl l.N+J l+j− sum limits j−1k=0S l.−J l+kA N−j+kA N
、
どこで j=1,2、...、J l;
B l.N−i=Bl l.N−i− sum N−ik=0S l.−N+i+kA k
どこで i=1,2、...;S l.−r=0、 もし r>J l;
beginalign&R l.0= fracB lN−1A N;&R li= fracB lN−1−i− sum limits i−1k=0R lkA N−i+kA N、 endalign qquad(5)
どこで i=1,2、...
最後の平等の右側の合計の条件 (4) 画像のローランシリーズの主要部分と通常部分をそれぞれ形成する X l(p) 求められた解決策 x l(t)、l in[1;L x] 無限遠点の近く。 画像のオリジナル X l(p) 一般化された機能を提供します x l(t)、l in[1;L x] 単数を含む x −l(t) そして定期的に x +l(t) コンポーネント。
そのため、目的のソリューションのメソッドの分析部分を実行した後 x l(t)、l in[1;L x] 方程式 (1) 次の説明が表示されます。
x l(t)=x −l(t)+x +l(t)= sum −J lj=0S lj rm delta j(t)+ sum inftyi=0R l.iti/i!、 qquad(6)
どこで rm delta j(t) -ゼロからのインパルス関数 −J l 考慮された計算間隔の初期点で定義された-th次を含む; S l.j -インパルス関数の重み係数; R l.i 解の正規成分の展開係数は x +l(t) 横座標を含む考慮された計算間隔の初期点の右近傍のべき級数で t=0+ [9,10]。
受け取ったフォーム (6) 希望するソリューションの説明 x l(t)、l in[1;L x] は、非線形非自律システムのダイナミクスの定性的特徴の分析に関連するいくつかの基本的なポイントを反映しています。 ラプラス積分変換を使用すると、現在の計算間隔の開始点に対応するポイントで、既知の初期条件から初期条件への正しい遷移が決定され、目的の解の方程式が強調表示されます。 (1) 存在する場合、最初の種類の休憩。 説明の存在 (6) 特異成分 x −l(t) 既存の微分可能な第1種のギャップを区別する可能性を示します。 解の特異成分は x −l(t) 存在する場合、メソッドの分析部分の現在の計算ステップの開始に対応する離散時間での決定に使用できます。
通常のソリューションコンポーネント x +l(t) 説明から次のように (6) は、べき級数で表され、現在の計算間隔での計算には、メソッドの数値部分が使用されます。 メソッドの数値部分は、独立変数の離散化に基づいています t 。 現在の計算間隔で rm[t k−1;t k] rm、 rmt k=t k−1+h k メソッドの数値部分の実装は、適切なステップサイズの選択から始まります。 h=h k 。 この選択は、次の等式[9.10]によって管理されます。
h=q rm tau、 qquad(7)
どこで 0<q<1。
限界値 tau 現在の計算ステップの長さ h 平等に含まれる (7) 、通常の成分のべき級数の数値的優勢を計算するための現在の間隔の収束の研究の結果があります x +r\左(t\右) 必要なソリューション x r(t)r=1,2、 dot、L x 。 現在の計算ステップの長さ h=h k 平等に従って選択 (7)、非線形非自律システムのダイナミクスの定性的特徴を分析するための多くの重要な条件を確実に満たすようなものです。
まず、現在の計算間隔で[t_k−1;t_k],t_k=t_k−1+h_k 通常のコンポーネントソリューションのすべてのべき級数 x_r+(t)それらに配置された関数に収束し、テイラーランクになります。これは、考慮された時間間隔内に目的のソリューションが存在することを示します。x_r+(t)計算手順全体に論理的な意味と実際的な便宜を与える。
第二に、平等に従って選択(7) 計算ステップ値 h=h_k 離散時刻での計算手順の数値安定性を提供します t=t_k おおよその値 x_l+(t_k;I_l) 通常のコンポーネント x_l+(t) 求められた解決策 x_l(t),l∈[1;L_x] 。 解のおおよその値の計算 x_l+(t_k;I_l) 解の正規成分のテイラー級数の制限に関連 x_l+(t) 彼の最初の部分的な合計 I_lメンバー。この場合に発生する系列の残差メンバーは、ローカル計算エラーを形成し、常に制限され、[9、10]で与えられた式を使用した上限推定に利用できます。
第三に、歩幅h=h_k 通常のコンポーネントの変化率に常に対応する x_r+(t)希望するソリューション。この結果は、ソリューションの通常のコンポーネントのべき級数の収束に関する研究の組織によって保証されますx_r+(t)対応する数値の過半数を考慮することにより。それらのメンバーは、これらのべき級数の係数のすべての可能な組み合わせによって形成され、離散時間でのこれらのコンポーネントソリューションから有限次数の導関数の値を決定します。t=t_k−1 。
第四に、平等 (7) 計算ステップ値 h=h_k 上位評価の手順を整理できます |Δx_l+(t;I_l)|t=t_k 近似値計算の絶対合計誤差 x_l+(t_k;I_l) 通常のコンポーネント x_l+(t) 求められた解決策 x_l(t),l∈[1;L_x] 。合計計算誤差とは、2つ以上の計算ステップを実行した後に蓄積された誤差を意味し、それぞれで局所的な計算誤差が発生します。
だから、平等に従って選択する(7) 現在の計算ステップの値 h=h_k 解の正規成分のテイラー級数を制限する x_l+(t) 彼の最初の部分的な合計 I_l 用語、おおよその値を計算する x_l+(t_k;I_l),t_k=t_k−1+h_kソリューションのこのコンポーネント。次に、現在のステップで評価するh=h_k ローカル計算エラー、上限推定値を計算 |Δx_l+(t;I_l)|,t=t_k合計計算エラー。この方法で得られた数値結果は、離散時間を可能にしますt=t_k 縦座標軸で、未知の正確な値を含む1次元間隔を選択します x_l+(t_k) 通常のコンポーネント x_l+(t)目的のソリューション。受け入れられた表記法では、この間隔は離散時間でt=t_k 次の二重不等式について説明します。
x_l+(t_k;I_l)−|Δx_l+(t_k;I_l)|≤x_l+(t_k)≤x_l+(t_k;I_l)+|Δx_l+(t_k;I_l)|.(8)
平等 (6) そして二重不等式 (8) 現在の計算ステップでの数値解析法の計算手順の結果を説明する h=h_k 。 所定の学習間隔で次の計算ステップを実行するには [t_0;T] 縦座標軸は量だけ右にシフトされます h_k 。 その後、二重不等式から選択 (8) で l=r,r=1,2,…,L_x初期条件のおおよその値については、メソッドの分析部分と数値部分について説明した手順を繰り返します。
### **非線形非自律システムのダイナミクスの情報指標と分析数値法の計算スキームのパラメーターの関係を確立する**
式の分析(3) 方程式を考慮に入れる (2) 極間の数学的関係を確立することにより、この目標を達成できることを示しています rm lambda n、 rmn=1,2、...、N rm 画像 X l(p) 求められた解決策 x l(t)、l in[1;L x] 通常のコンポーネントの定性的な機能とプロパティの動的なインジケータ x +l(t) この決定の。 ソリューションの通常のコンポーネントの動的な指標として x +l(t)、l in[1;L x] 論理的かつ実質的に動機付けられた係数の検討 R l.i 説明に含まれる (6) パワーシリーズ。 オッズ計算 R l.i 再帰式を使用してメソッドの分析部分で実行します (5) 。 マトリックス分析を使用してこれらの式を変換すると、新しい形式の記録が行われ、係数間の必要な数学的関係が明示的な形式で確立されます R l.i 決定の通常の部分 x +l(t) と極 rm lambda n、 rmn=1,2、...、N rm 画像 X +l(p) このコンポーネント。 係数を計算するための新しい式 R l.i [8]に記載されています。 したがって、たとえば、すべての極が rm lambda n、 rmn=1,2、...、N rm 画像 X +l(p) 係数を計算するための単純な式 R l.i 次の形式があります[8]:
R l.i= sum Nn=1r l.n\ラムダ in、i in ge left| bfZ right|。 qquad(9)
オッズ r l.n この場合、次の式で計算します。
r l.n= frac sum limits im=1B ∗l.N−1−m\ラムダ −mnN+ sum limits N−1m=1(N−m)A ∗N−m\ラムダ −mn。 qquad(10)
オッズ B ∗l.N−1−m、m in\左| bfZ\右| そして A ∗r、r=1,2、...、N−1 式で (10) 係数に関連 B l.N−1−m、A r 式に含まれる (4) 、次の関係により:
beginalign&B ∗l.N−1−m= fracB l.N−1−mA N;&A ∗r= frac−A rA N。 endalign
フォーミュラ (9) 説明を書くことができます (6) 通常のコンポーネントのべき級数 x +l(t) この場合の望ましい解決策は、次の新しいフォーム[8]にあります。
x +l(t)= sum inftyi=0 fracR l.it ii!= sum inftyi=0 sum N mn=1 fracR [n]lit ii!、 Qquad(11)
どこで N m -この場合、単純なイメージポールの数 X +l(p) 。
形成された説明 (11) 通常のコンポーネントの条件 x +l(t) 求められた解決策 x l(t)、l in[1;L x] 次の同等の表現:
x +l(t)= sum N mn=1x [n]l(t)。 qquad(12)
構成部品 x [n]l 次の説明があります。
x [n]l(t)= sum inftyi=0 fracR [n]l.it ii!。 qquad(13)
相互接続された平等システム (11)−(13) 平等の有向変換の結果 (6) ソリューションの通常のコンポーネントの初期説明 x +l(t) 。 それによれば、計算の各ステップで、極での解のこの成分の分解が可能です rm lambda n、 rmn=1,2、...、N rm 彼女の画像 X +l(p) 。 予想通り、分解は絶対的な性質ではありません。なぜなら、再帰的に計算された係数を通して B ∗l.N−1−m、m in\左| bfZ\右| 式に含まれる (10) 、非線形非定常システムの場合、そのダイナミクスの形成で支配的なすべての要素間の関係は常に保持されます (13) 提出 (12) 。 通常のコンポーネントの分解 x +l(t) 求められた解決策 x l(t)、l in[1;L x] 平等のシステムによって記述される (11)−(13) は、解の存在と一意性を調べる手順の形式化、計算ステップの選択、およびそのような計算の絶対局所誤差の推定に関連する計算コストの最適化に関連するいくつかの特別な問題の解決に成功しました[9]。
要約すると、非線形非自律システムのダイナミクスの定性的特徴を研究するために、次のアルゴリズムを定式化します。 最初に、元の方程式の同等の変換を実行します (1) マトリックスが気になるシステムダイナミクス A(D) ヤコビ関数行列と一致し、極 rm lambda n、 rmn=1,2、...、N rm 画像 X +l(p) この行列の固有値と一致します。 ソリューションの通常のコンポーネントの後続の分解 x +l(t) これらの数値については、必要な研究のための設計スキームを編成する機会を提供します。 システムのダイナミクスの定性的特徴の非定常情報インジケータの役割では、所定の研究間隔の変化を記述する関数を検討します 固有値 機能的なヤコビ行列と要素 分解 決定の通常の部分 。 方程式の望ましい解の提案された分解スキーム 固有値によって、この方程式に対応する関数ヤコビ行列はそれ自体異常です。 これにより、期待される結果の新規性、その解釈、およびその後のアプリケーションの見通しが決まります。 そのような問題についての判断の完全性は時間の問題であるため、それらのうちのいくつかについてのみ言及します。
非定常固有値の実数部の符号 離散時間ごとの関数ヤコビ行列 各要素に関する安定性と不安定性の間隔の境界を区別できるようにする 分解 。 このような情報は、意思決定の通常の構成要素の安定条件間の因果関係を識別するために重要です。 および要素自体の同様の条件 このコンポーネント。 通常のコンポーネントの安定性または不安定性の条件 求められた解決策 この場合、それらは非定常固有値間の存在の結果になります 1つ以上の支配的なものの機能的ヤコビ行列、およびそれらの性質の変化を含む、研究間隔におけるこれらの支配的な数の相互作用の特性。
分解要素の動的インジケータ 非定常固有値と組み合わせて 関数ヤコビ行列は、二重不等式で記述される非線形非自律システムのダイナミクスを計算した結果の異なる解釈の初期位置を決定します 。 二重不等式の指標の計算における数学的関係と相関 不平等のような二重不等式 しかし、対応する分解要素について 、システムの動的プロパティの不規則性により、分解の要素間の特徴的な関係と組み合わせを強調するための基礎として機能します 方程式の望ましい解 パラメータの変化とシステムの外部の影響に最も敏感です。 この場合に得られた結果の分析により、分岐の発生を決定する条件、または位相軌道の「混合」につながる初期条件の範囲を選択することが可能になります[5]。
与えられた学習間隔の変化を表す機能の定性的特徴と特性 非定常固有値 これらの関数の連続性と単調性、極値点の存在、そのような数の性質の変動性、それらの実部の符号を含む機能的ヤコビ行列は、間違いなく方程式の内部因果関係の本質を反映しています 。 この結果、これらの関数の機能とプロパティは、非線形非自律システムのダイナミクスの定性的機能の高度に適応性のあるインジケータです。 コンテンツスペクトルの多様性とそのようなシステムダイナミクスの指標の発現の変動性はまだ決定されておらず、これは独立したタスクを構成し、その解決策は、おそらく、非線形の学習対象の複雑で曖昧な動作をより完全に理解するための出発点として役立つでしょう。 これらの機能指標と非線形非自律システムの定性的特徴との関係の分離と分類は、通常のダイナミクスまたは決定論的カオスへの移行の条件の決定を含む、非線形および非定常現象の分析のための新しい計算アルゴリズムの出現につながるはずです[2-5]。
おわりに
平等のシステムによって説明される 方程式の望ましい解の正規成分の分解 は、非線形非自律システムのダイナミクスを分析するための独立したコンピューティングツールとして、関数ヤコビ行列の固有値を導入し、アクティブにします。 分解要素の機能と動的プロパティを生成します。 。 次の例に示すように、このような機能の分析と分解要素の動的特性 非線形ダイナミクスの特性の1つである「剛性」[1,4,5]の存在に関する新しい条件の特定につながります。
前述のことを要約すると、非線形ダイナミクスの定性的特徴と特性の発現には多くの変種があり、それらは外観条件と発現の形態の両方の点で多様であることに注意してください。 そのようなダイナミクスの特性としての不規則性は、例外ではなく標準です[2]。 非線形非自律システムのこのような複雑で予測不可能なダイナミクスの理由は、ダイナミクス方程式の内部パラメトリック関係の構造と構成に固有のものです 。 もちろん、そのような関係の包括的な指標の構成要素の1つは固有値です 機能的なヤコビ行列。 ダイナミクス方程式の望ましい解の分解に基づいた非線形非自律システムのダイナミクスの定性的特徴の分析 それぞれが固有値の1つに対応するコンポーネントに 機能的なヤコビ行列は、これらのコンポーネント間の論理的および数学的な関係を維持しながら、関連する研究と新しい方法論を実施するための提案されたアプローチの本質を反映しています。
例
この方程式に対応するヤコビ関数行列の固有値による動的方程式の解の分解に基づく非線形自律システムのダイナミクスの定性的特徴の研究。
ユニフォームで 考慮される非線形自律システムのダイナミクス方程式の形式は次のとおりです。
$$表示$$ \ begin {equation} \ left \ | \ begin {array} {cc} {a \ _ {1.1} ^ {[1]} D + a \ _ {1.1} ^ {[0]}}&{0} \\\\ {a \ _ {2.1 } ^ {[0]}}&{a \ _ {2.2} ^ {[1]} D} \ end {array} \、\ right \ | \、\左\ | \、\ begin {array} {c} {x \ _ {1}(t)} \\\\ {x \ _2(t)} \ end {array} \ right \ | = \左\ | \ begin {array} {c} {g \ _ {1.1} ^ {[0]}} \\\\ {0} \ end {array} \ right \ | f(t)+ \ left \ | \ begin {配列} {c} {h \ _ {1.1} x \ _ {1} ^ 2(t)x \ _2(t)} \\\\ {h \ _ {2.1} x \ _ {1} ^ {2 }(t)x \ _ {2}(t)} \ end {array} \ right \ |、\ qquad(14)\ end {equation} $$ display $$
どこで
方程式の説明に示されているパラメーターの値を代入した後 、この方程式の次の統一された形式を取得しました。
$$表示$$ \ begin {equation} \ left \ | \ begin {array} {cc} {D {\ rm + B + 1}}&{0} \\\\ {-B}&{D} \ end {array} \ right \ | \、\左\ | \ begin {array} {c} {x \ _ {1}(t)} \\\\ {x \ _ {2}(t)} \ end {array} \ right \ | = \左\ | \ begin {array} {c} {A} \\\\ {0} \ end {array} \ right \ | \デルタ\ _ {1}(t)+ \左\ | \ begin {array} {c} {x \ _ {1}(t)^ {2} x \ _ {2}(t)} \\\\ {-x \ _ {1}(t)^ {2 } x \ _ {2}(t)} \ end {array} \ right \ | 。 \ end {式} \ qquad(15)$$表示$$
方程式 「brusselator」方程式として知られるは、その解の定性的特徴がパラメータ間の関係に実質的に依存するため、ユニークです。 そして [4]。 で 安定したリミットサイクルが存在するHopf分岐があります。 安定した定常解点に行きます 条件に対応 。 分岐関係 方程式の解の特徴と特性の発現の性質の境界を設定します パラメーター間の関係に応じて そして 。 方程式の解のダイナミクスの分岐性 この方程式に対応する関数ヤコビ行列の固有値の非定常特性の特徴、および分解要素のダイナミクスに反映されます 、 そのような固有値によるこれらの解の。 この関係の数学的特徴と因果関係の特定は、検討中のシステムのダイナミクスの定性的特徴の研究に対する提案されたアプローチの方法論的基礎を構成します。
それに応じてマトリックスを埋める 方程式の選択された線形部分 マトリックスのため ヤコビ行列との一致を保証するために、システムのダイナミクスに関する次の同等の説明を得ました[9,10]:
$$表示$$ \ begin {equation} \ left \ | \ begin {array} {cc} {D + B + 1 {\ rm -2R} \ _ {1.0} {\ rm R} \ _ {2.0}}&{{\ rm -R} \ _ {1.0} ^ {2}} \\\\ {-B + {\ rm 2R} \ _ {1.0} {\ rm R} \ _ {2.0}}&{D + {\ rm R} \ _ {1.0} ^ {2}} \ end {array} \ right \ | \、\左\ | \ begin {array} {c} {x \ _ {1}(t)} \\\\ {x \ _ {2}(t)} \ end {array} \ right \ | = \左\ | \ begin {array} {c} {A} \\\\ {0} \ end {array} \ right \ | \デルタ\ _ {1}(t)+ \左\ | \ begin {array} {c} {x \ _ {1}(t)^ {2} x \ _ {2}(t){\ rm -2R} \ _ {1.0} {\ rm R} \ _ { 2.0} x \ _ {1}(t){\ rm -R} \ _ {1.0} ^ {2} x \ _ {2}(t)} \\\\ {-x \ _ {1}(t )^ {2} x \ _ {2}(t)+ {\ rm 2R} \ _ {1.0} {\ rm R} \ _ {2.0} x \ _ {1}(t)+ {\ rm R} \ _ {1.0} ^ {2} x \ _ {2}(t)} \ end {array} \ right \ | 、\ end {equation} \ quad(16)$$表示$$
どこで そして 解の正規成分の展開における非ゼロ係数 べき級数で。 方程式を実行することにより 次の形式の分析数値法の分析部分の計算手順 目的のソリューションについて次の説明を入手しました。
どこで -希望するソリューションの通常のコンポーネントのべき級数の係数 計算式により計算 で そして 非定常固有値の使用 関数ヤコビ行列方程式 。
希望するソリューションのために形成 方程式 説明 特異な成分を含まないもの。 所定の調査間隔[0;の各計算ステップでの分析数値法の数値部分 10]は、標準スキームに従って実装されます。 計算の絶対ローカルエラーの所定の制限レベルを使用したシステムのダイナミクスの計算結果 および前提条件 場合のために 図1に示す。 図からわかるように、考慮される非線形自律システムのダイナミクスは、安定したリミットサイクルによって特徴付けられます[4]。 そのようなダイナミクスの特徴は、「剛性」、つまり 特性方程式の高速および低速変化のセクションの交代 。 ただし、 図2からわかるように 、非線形の場合と線形の場合の基本的な違いは、指数が このような「除去」は一定ではなく、時間とともに継続的に変化します。 時間間隔[3-4]、[8-9]で、目的の解が十分に速く変化すると、不安定なインジケータ 、ダイナミクスのこの特徴を反映して、比較的高い値に達し、最大100ユニットに達します。 時間から 決定のかなり遅い変化で間隔の始まりを決定し、指標 時間間隔[4〜8]で1に近い値を取る連続して減少し、これらのソリューションに高速コンポーネントがないことを示します。 したがって、非線形ダイナミクスの定性的特徴としての「剛性」は、非定常インジケーターによって特徴付けられます 。 非線形ダイナミクスの本質を反映したこのインジケーターの継続的な変化は、自己組織化の基本原則を明らかにしています。 固有値の計算方法 ヤコビ行列は、計算の2番目のステップから始まり、計算された近似初期値の関数であるようなものです そして 希望するソリューション。 順番に、式に従って 、 、これらの固有値は動的メトリックを直接決定します 現在の計算ステップの最後に目的のソリューション。 したがって、計算の各ステップ内で、ダイナミクス制御、したがって非定常の「剛性」インジケータ このダイナミクスは、方程式自体の内部座標-パラメトリック関係を介して実行されます 。 これらの内部関係は、動的インジケーターを介して実装されます。 決定の 一方では、固有値に依存します 機能的なヤコビ行列、そして一方で、「剛性」を決定する システムの非線形ダイナミクス。 言い換えれば、システムの非線形ダイナミクスは適応制御のすべての機能を備えています。なぜなら、このダイナミクスの品質特性であり結果である「剛性」はこのダイナミクスによって生成され、ヤコビ行列の固有値を介して因果関係を生成するためです。
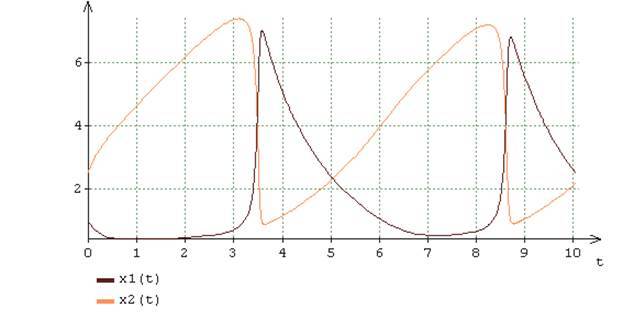
図1 方程式の近似解 A = 2の場合、B = 6方程式の望ましい解の指標 。
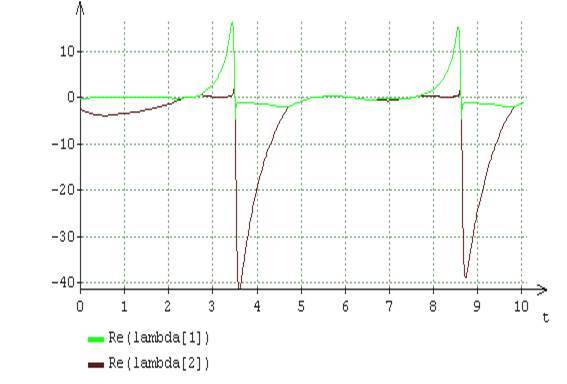
明らかになった「剛性」現象の解析に必要な計算結果を図に示します。 2-4。 これらの結果は、表現に基づいて実装された結果に対応しています。 - で そして 分解ソリューション 方程式 固有値による 機能的なヤコビ行列。 したがって、たとえば、図2は、非定常固有値の実数部と虚数部の変化のグラフを示しています 関数ヤコビ行列方程式 。 これらのグラフによれば、線形自律システムの場合のように、「剛性」は、モジュロを法とする最大根と最小根の実数部の絶対値の互いからの距離によって特徴付けられます。
(a)

(b)
図2。 固有値の実部(a)および虚部(b)のダイナミクス A = 2、B = 6の関数ヤコビ行列
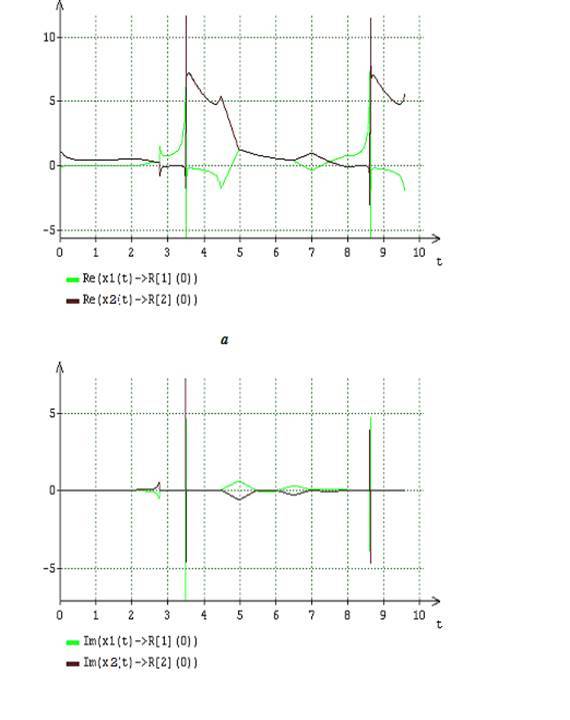
図3 2つのコンポーネントの材料(a)および虚数(b)のダイナミクス(13)、 求められた解決策 式(16)A = 2、B = 6
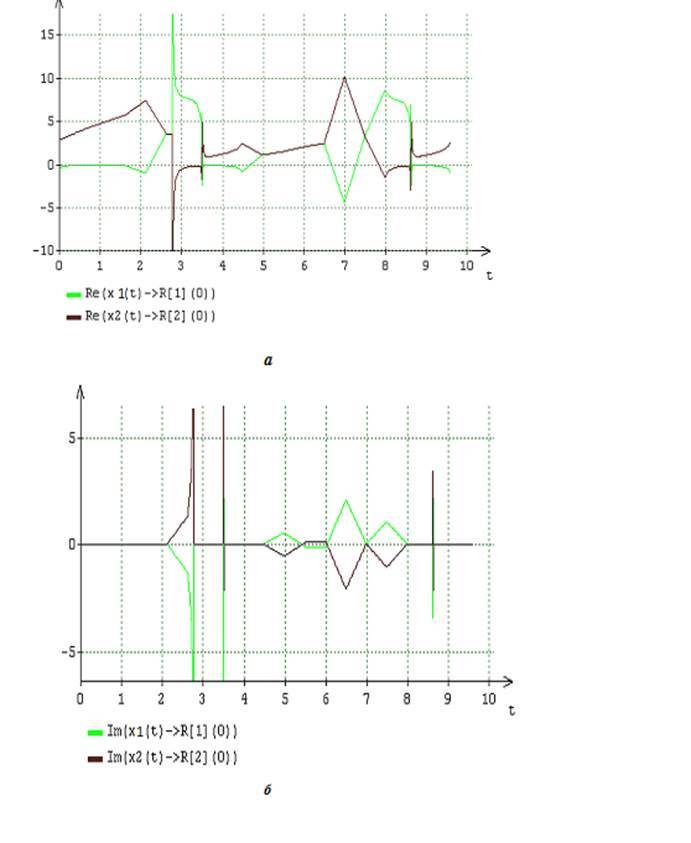
図4 2つのコンポーネントの材料(a)および虚数(b)のダイナミクス(13)、 (16) A = 2, B = 6
[0-10] , 。 , 。 , .2, , . , , . , , , , . : 。
, , 、 , 、 。 [0 -2,5] [4 -6,5], , , .1,3,4 , , 、 , 、 , . 、 , . , - .
[3 — 4] [7 — 8], , .1,3,4 , , , 、 , , , . 、 , .2 . 、 , . -. , , .3 , 、 , .4, , , 。 , , 、 .
, , , .5-8. ,
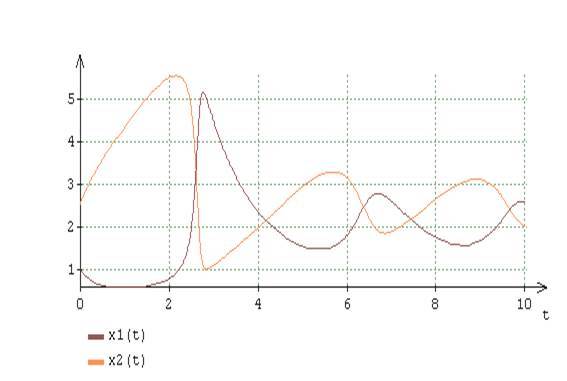
図5 (16) A = 2, B = 5
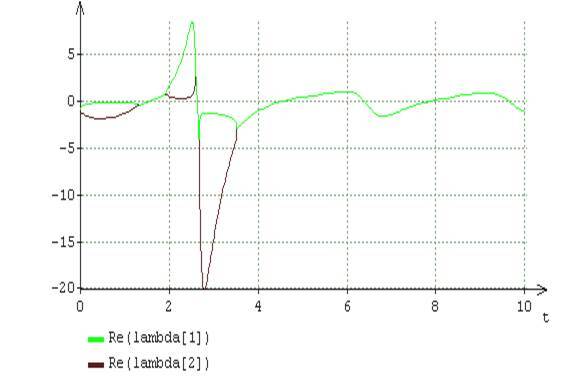
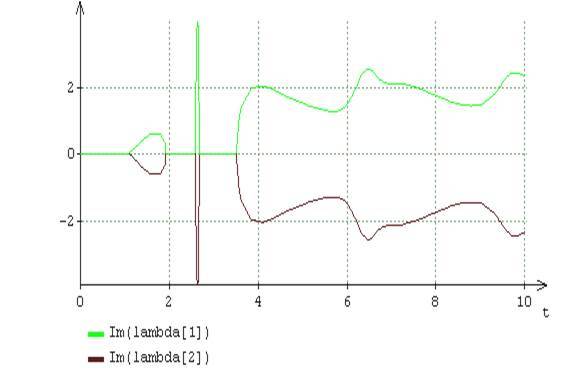
図6 () () (16) A = 2, B = 5
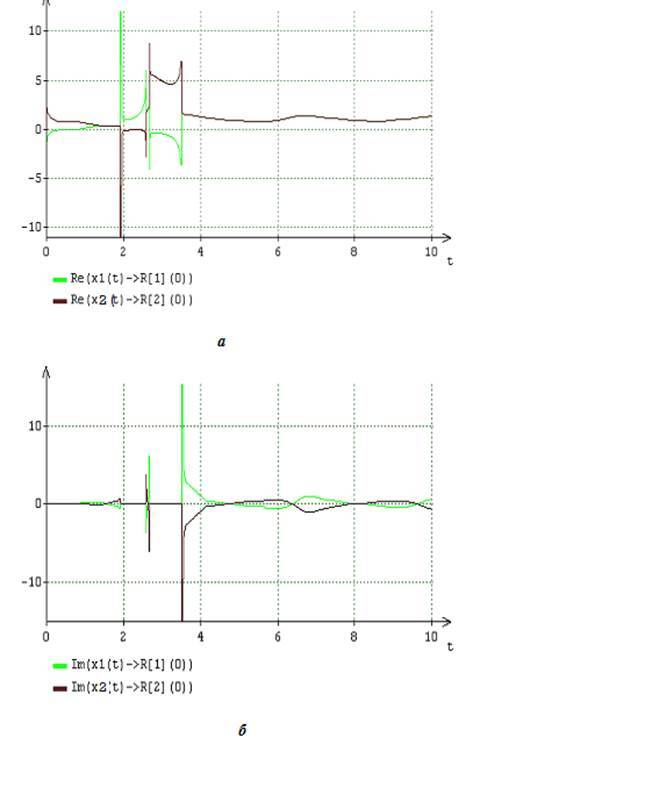
図7 () () (13) (16) A = 2, B = 5
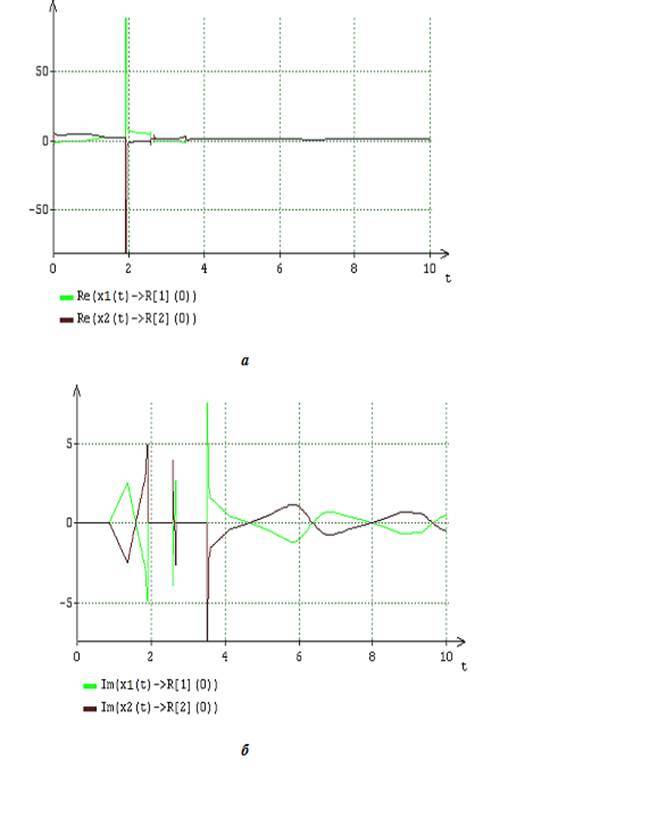
図8 () () (13) (16) A = 2, B = 5
, ,
.5 で , , , : 。 , .6-8, で そして 。
.6 そして 。 .6 , . .2 , , . , , , , , , .
.5 , «». , , . 、 , - . , «» , , , .
、 , . , .3,4 .7,8 , , 、 。 , 、 . .7,8 . , , , - 、 。
参照資料
- .., .., .. . – .: , 1990. – 256 .
- . . . – .: , 1985. – 423 .
- .. . . –.: , 2000. –352 .
- ., ., . . / . 英語から .. , .. (.) – .: , 1990. –512 .
- .., .., .., .. .- .: , 1991.-240.
- .., .., .. MATLAB / -
. – ., 1996. –192 . - .. . – .: , 1997. – 206 .
- .., .., .. . –.: ., 1989. – 447 .
- .., .. - . – , . ., , - , 2002. – 368 .
- Bychkov Yu.A.、Scherbakov S.V. 集中および分布した非定常パラメータを持つ動的システムの決定論的非線形モデルの解析的および数値的計算。第2版、改訂および補足。SPb。:SPbGETU「LETI」の出版社、2014年。-388 p。