DODとは何ですか?
この記事は、その本質を説明しようとせずに異なるアプローチを比較する試みとして考案されました。 Habréには、テーマに関する記事がいくつかあります。たとえば、 CppConカンファレンスのビデオもご覧ください 。 しかし、簡単に言えば、 DODはキャッシュフレンドリーな方法でデータを処理する方法です。 理解できないように聞こえますが、例を挙げて説明します。
例
#include <chrono> #include <iostream> #include <vector> using namespace std; using namespace std::chrono; struct S { uint64_t u; double d; int i; float f; }; struct Data { vector<uint64_t> vu; vector<double> vd; vector<int> vi; vector<float> vf; }; int test1(S const & s1, S const & s2) { return s1.i + s2.i; } int test2(Data const & data, size_t const ind1, size_t const ind2) { return data.vi[ind1] + data.vi[ind2]; } int main() { size_t const N{ 30000 }; size_t const R{ 10 }; vector<S> v(N); Data data; data.vu.resize(N); data.vd.resize(N); data.vi.resize(N); data.vf.resize(N); int result{ 0 }; cout << "test #1" << endl; for (uint32_t i{ 0 }; i < R; ++i) { auto const start{ high_resolution_clock::now() }; for (size_t a{ 0 }; a < v.size() - 1; ++a) { for (size_t b{ a + 1 }; b < v.size(); ++b) { result += test1(v[a], v[b]); } } cout << duration<float>{ high_resolution_clock::now() - start }.count() << endl; } cout << "test #2" << endl; for (uint32_t i{ 0 }; i < R; ++i) { auto const start{ high_resolution_clock::now() }; for (size_t a{ 0 }; a < v.size() - 1; ++a) { for (size_t b{ a + 1 }; b < v.size(); ++b) { result += test2(data, a, b); } } cout << duration<float>{ high_resolution_clock::now() - start }.count() << endl; } return result; }
2番目のテストは30%速く実行されます(VS2017およびgcc7.0.1で)。 しかし、なぜですか?
S
構造のサイズは24バイトです。 私のプロセッサ(Intel Core i7)には、コアあたり32KBキャッシュと64Bキャッシュラインがあります。 つまり、メモリからデータを要求する場合、2つの
S
構造のみが1つのキャッシュラインに完全に収まります。 最初のテストでは、1つの
int
フィールドのみを読み取りました。 1つのメモリアクセスで、1つのキャッシュラインに必要なフィールドは2つ(場合によっては3つ)になります。 2番目のテストでは、同じ
int
値を読み取りますが、ベクターから読み取ります。
std::vector
はデータの一貫性を保証します。 これは、1つのキャッシュラインでメモリにアクセスするときに、16(
64B / sizeof(int) = 16
)の値が必要になることを意味します。 2番目のテストでは、メモリへのアクセス頻度が低くなります。 ご存知のように、メモリアクセスは、最新のプロセッサでは弱いリンクです。
実際にはどのようになっていますか?
上記の例は、 AoS (構造体の配列)の代わりにSoA (配列の構造体)を使用する利点を示していますが、この例は
Hello World
カテゴリ、つまり 実生活とはほど遠い。 実際のコードには、多くの依存関係と特定のデータがありますが、おそらくパフォーマンスは向上しません。 さらに、テストで構造のすべてのフィールドを参照する場合、パフォーマンスに違いはありません。
アプローチの適用の現実を理解するために、両方の手法を使用して多少複雑なコードを記述し、結果を比較することにしました。 ソリッドの2Dシミュレーションとします-N個の凸ポリゴンを作成し、質量、速度などのパラメーターを設定します。 30 fpsに留まることをシミュレートできるオブジェクトの数を確認します。
1.構造の配列
1.1。 プログラムの最初のバージョン
プログラムの最初のバージョンのソースコードは、 このコミットから取得できます。 次に、コードについて簡単に説明します。
簡単にするために、プログラムはWindows用に作成されており、レンダリングにDirectX11を使用しています。 この記事の目的は、プロセッサーのパフォーマンスを比較することなので、グラフィックスについては説明しません。 肉体を表す
Shape
クラスは次のようになります。
Shape.h
class Shape { public: Shape(uint32_t const numVertices, float radius, math::Vec2 const pos, math::Vec2 const vel, float m, math::Color const col); static Shape createWall(float const w, float const h, math::Vec2 const pos); public: math::Vec2 position{ 0.0f, 0.0f }; math::Vec2 velocity{ 0.0f, 0.0f }; math::Vec2 overlapResolveAccumulator{ 0.0f, 0.0f }; float massInverse; math::Color color; std::vector<math::Vec2> vertices; math::Bounds bounds; };
-
position
とvelocity
の目的は明らかだと思います。vertices
ランダムに与えられた図の頂点。 -
bounds
形状を完全に含む境界ボックス-交差点の事前チェックに使用されます。 -
massInverse
は、質量で除算された単位です。この値のみを使用するため、質量の代わりに格納します。 -
color
-color-レンダリング中にのみ使用されますが、形状のインスタンスに保存され、ランダムに設定されます。 -
overlapResolveAccumulator
以下の説明を参照してください。
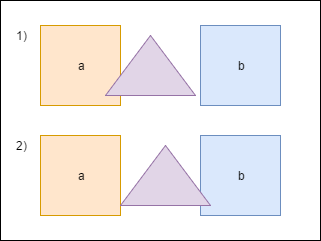
三角形が図形aと交差する場合、図形が重ならないように少し移動する必要があります。 また、
bounds
を再カウントする必要があり
bounds
。 しかし、三角形を移動した後、別の図形-bと交差し、再び移動して
bounds
カウントする必要があり
bounds
。 2番目の移動の後、三角形は再び図aの上になります。 計算の繰り返しを避けるために、三角形を移動するために必要な値を特別なバッテリーに
overlapResolveAccumulator
そして、後でこの値にフィギュアを移動しますが、一度だけです。
プログラムの中心は、
ShapesApp::update()
メソッドです。 以下はその簡略版です。
ShapesApp.cpp
void ShapesApp::update(float const dt) { float const dtStep{ dt / NUM_PHYSICS_STEPS }; for (uint32_t s{ 0 }; s < NUM_PHYSICS_STEPS; ++s) { updatePositions(dtStep); for (size_t i{ 0 }; i < _shapes.size() - 1; ++i) { for (size_t j{ i + 1 }; j < _shapes.size(); ++j) { CollisionSolver::solveCollision(_shapes[i].get(), _shapes[j].get()); } } } }
各フレームで
ShapesApp::updatePositions()
メソッドを呼び出します。このメソッドは、各形状の位置を変更し、新しい
Shape::bounds
を計算し
Shape::bounds
。 次に、各図の交差点
CollisionSolver::solveCollision()
ます。 軸分離定理(SAT)を使用しました。 これらすべてのチェックを
NUM_PHYSICS_STEPS
回行います。 この変数にはいくつかの目的があります。1つ目は物理がより安定し、2つ目は画面上のオブジェクトの数を制限することです。 C ++は高速で非常に高速であり、この変数がなければ何万もの形状があり、レンダリングが遅くなります。
NUM_PHYSICS_STEPS = 20
を使用し
NUM_PHYSICS_STEPS = 20
私の古いラップトップでは、このプログラムはfpsが30を下回り始めるまでに最大500個を計算します。Fuuuu、わずか500 ???! 少し同意しますが、すべてのフレームが20回計算を繰り返すことを忘れないでください。
スクリーンショットで記事を希釈する価値があると思うので、ここに:
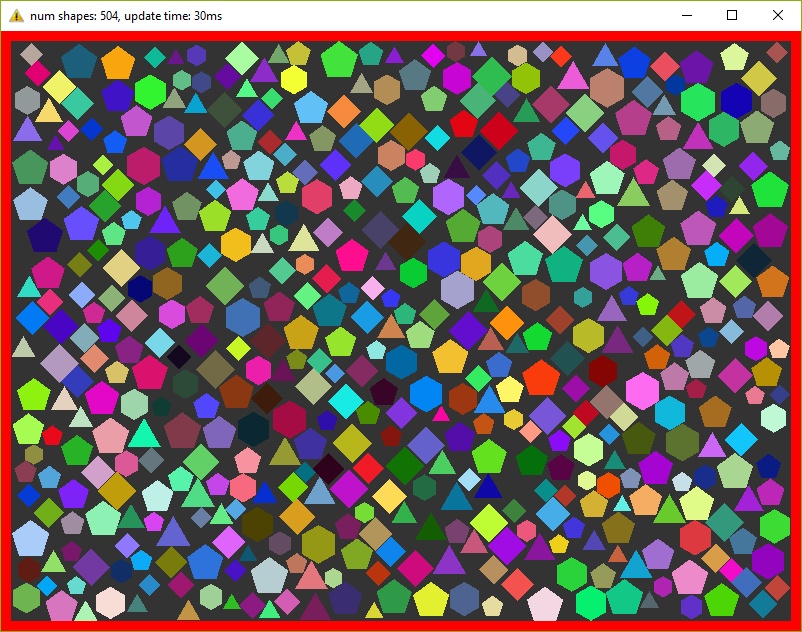
1.2。 最適化番号1.空間グリッド
私は、できるだけ現実に近いプログラムでテストを実施したいと述べました。 上記で書いたものは、実際には使用されません-各スーと各図をゆっくりチェックするために。 計算を高速化するために、通常、特別な構造が使用されます。 NxMセルで構成される
Grid
と呼ばれる通常の2Dグリッドを使用することをお勧めします。 計算の開始時に、各セルに含まれるオブジェクトを記録します。 次に、すべてのセルを調べて、オブジェクトのいくつかのペアの交差を確認するだけです。 私はリリースでこのアプローチを繰り返し使用してきましたが、非常に迅速に記述され、簡単にデバッグされ、理解しやすいことが実証されています。
プログラムの2番目のバージョンのコミットは、 ここで確認できます 。 新しい
Grid
クラスが登場し、
ShapesApp::update()
メソッドが少し変更されました-グリッドメソッドを呼び出して、交差をチェックします。
このバージョンでは、すでに30 fpsで8000個の数字を保持しています(各フレームで約20回の反復を忘れないでください) 数字がウィンドウに収まるように、数字を10倍減らす必要がありました。
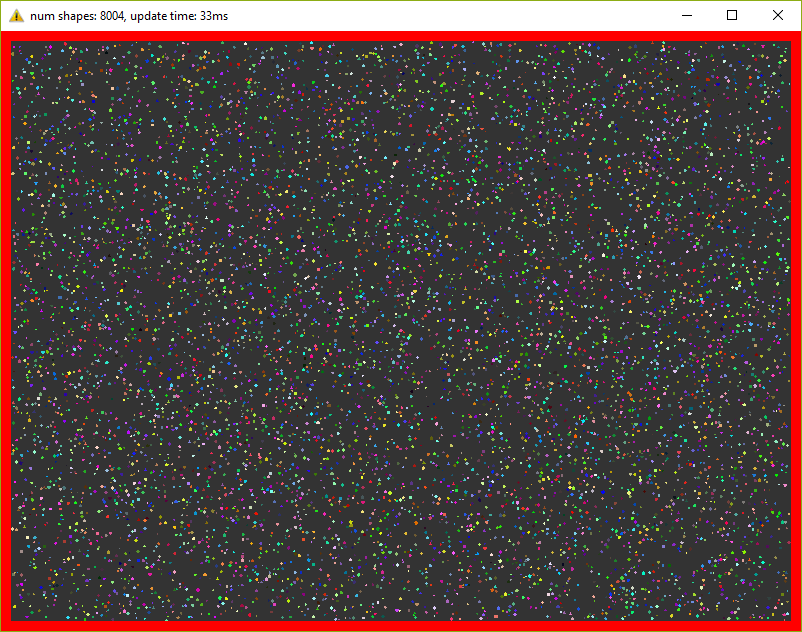
1.3。 最適化番号2。マルチスレッド。
今日、4つのコアを備えたプロセッサでさえ電話にインストールされている場合、マルチスレッドを無視するのは愚かなことです。 この最後の最適化では、スレッドのプールを追加し、メインタスクを等しいタスクに分割します。 そのため、たとえば、以前はすべての図形を実行し、新しい位置を設定して
bounds
を再
ShapesApp::updatePositions
する
ShapesApp::updatePositions
は、図形の一部に沿ってのみ実行されるようになり、1つのコアの負荷が軽減されます。 プールクラスは、ここから正直にコピーアンドペーストされました 。 テストでは、4つのスレッドを使用します(メインスレッドを考慮)。 完成版はこちらにあります 。
主なタスクを分離すると、少し頭痛がします。 したがって、たとえば、図がグリッド内のセルの境界を越える場合、同時に複数のセルになります。
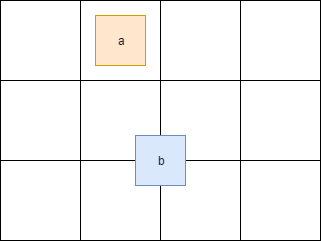
ここでは、図aは1つのセルにあり、 bは一度に4つのセルにあります。 したがって、これらのセルへのアクセスは同期する必要があります。 また、
Shape
クラスの一部のフィールドへのアクセスを同期する必要があります。 これを行うために、
std::mutex
を
Shape
および
Cell
追加しました。
このバージョンを実行すると、30 fpsで13,000の数値を観測できます。 非常に多くのオブジェクトに対して、ウィンドウを大きくしなければなりませんでした! そして再び-各フレームでシミュレーションを20回繰り返します。

2.配列の構造
2.1。 プログラムの最初のバージョン
上で書いたものを、私は伝統的なアプローチと呼んでいます-私は長年このコードを書いており、主に同様のコードを読みました。 しかし、ここで
Shape
構造を強制終了し、この小さな変更がパフォーマンスに影響するかどうかを確認します。 みんなの喜びに、リファクタリングは複雑ではなく、些細なことでさえありませんでした。
Shape
代わりに、ベクトルを持つ構造を使用します。
Shape.h
struct ShapesData { std::vector<math::Vec2> positions; std::vector<math::Vec2> velocities; std::vector<math::Vec2> overlapAccumulators; std::vector<float> massesInverses; std::vector<math::Color> colors; std::vector<std::vector<math::Vec2>> vertices; std::vector<math::Bounds> bounds; };
そして、この構造を次のように渡します。
solveCollision(struct ShapesData & data, std::size_t const indA, std::size_t const indB);
つまり 特定の数字の代わりに、それらのインデックスが送信され、メソッドでは必要なデータが必要なベクトルから取得されます。
このバージョンのプログラムは、30 fpsで500個の数値を生成します。 最初のバージョンと違いはありません。 これは、測定が少量のデータで実行され、さらに最も重い方法では構造のほとんどすべてのフィールドが使用されるためです。
さらに写真なしで、 それらは以前とまったく同じです。
2.2。 最適化番号1.空間グリッド
すべては以前と同じで、 AoSのみをSoAに変更します 。 コードはこちらです。 結果は以前よりも優れています-9500の数字(8000がありました)、つまり パフォーマンスの違いは約15%です。
2.3。 最適化番号2.マルチスレッド
繰り返しますが、古いコードを取り、構造を変更して、30 fpsで15,000の数値を取得します。 つまり 約15%のパフォーマンスの向上。 最終バージョンのソースコードはこちらです。
3.結論
当初、コードは、さまざまなアプローチ、そのパフォーマンス、および利便性をテストするために自分用に作成されました。 結果が示したように、コードを少し変更すると、かなり具体的な増加が見られます。 または、そうでない場合もあり、逆の場合もあります-生産性が悪化します。 たとえば、必要なインスタンスが1つだけの場合、標準的なアプローチを使用すると、メモリから1回だけ読み取り、すべてのフィールドにアクセスできます。 同じベクトル構造を使用して、各リクエストでキャッシュミスを使用して、各フィールドを個別にクエリする必要があります。 さらに、可読性がわずかに悪化し、コードがより複雑になります。
したがって、誰にとっても新しいパラダイムに移行する価値があるかどうかを明確に答えることは不可能です。 ゲームエンジンのゲーム開発者で働いたとき、生産性が10%向上したことは印象的な数字です。 ランチャーなどのユーザーユーティリティを作成したとき、 DODアプローチを適用しても同僚が困惑するだけでした。 一般に、自分で結論をプロファイリング、測定、および描画します:)。