👨‍👩‍👧‍👦 👩‍❤️‍👨 ⛰️ C ++メタプログラミングの実践：コンパイル時のバイナリ検索ツリー 🗒️ 👩🏽 🧜🏾

C ++のテンプレートの作成者は、一連の研究開発の基礎を築きました。C++テンプレート言語はチューリング完全 、つまりメタプログラム（コンパイル段階で動作するように設計されたプログラム）であり、C ++は計算可能なすべてを計算できることが判明しました。実際には、一般化されたデータ構造とアルゴリズムを記述するために、テンプレートの力が最もよく使用されます。STL（ 標準テンプレートライブラリ ）は生きた例です。

ただし、 variadic

テンプレート、type_traitsライブラリ、タプル、およびconstexpr

備えたC ++ 11の登場によりconstexpr

メタプログラミングはより便利で視覚的になり、特定のコンパイラーまたは複雑なマルチストーリーの拡張を使用してのみ実装できた多くのアイデアの実装への道が開かれましたマクロ。

この記事では、コンパイル時検索用のバイナリツリーの実装、つまりタプルの論理的な「拡張」であるデータ構造を開発します。バイナリツリーをテンプレートとして実装し、メタプログラミングを実践します。アルゴリズムをC ++テンプレート言語に移植するだけでなく、再帰的に移植します。

内容

理論のビット

最初に、データ構造とアルゴリズムに関するいくつかの定義と概念を思い出しましょう。読者がグラフ理論の基礎に精通している場合、および/または二分木とその準備方法を想像している場合は、このセクションをスキップして実装の詳細に直接進むことができます。

定義など：

フリーツリー（専用ルートのないツリー）または単なるツリーは、非循環無向グラフです。

ルートを持つツリー - ルート （ルート）と呼ばれる、1つの頂点が選択されているフリーツリー。

ノード -ルートを持つツリーのノード。

親ノードまたはノードXの親は、ルートRからこのノードXへのパス上でXに先行する最後のノードです。この場合、ノードXは記述された親ノードYの子と呼ばれます。ツリーのルートには親がありません。

リーフは、子ノードを持たないノードです。

内部ノードは、リーフではないノードです。

ノード X の次数は、このノードXの子ノードの数です。

ノード X の深さは、ルートRからこのノードXまでのパスの長さです。

ノードの高さ （高さ）-ノードからシートまでの最も単純な（リターンなし）下向きパスの長さ。

ツリーの高さ-このツリーのルートの高さ。

順序付けられたツリーは、各ノードの子ノードが順序付けられているルートを持つツリーです（つまり、子ノードのセットの1からkまでの自然数のセットへのマッピングが指定されます（ kはこのノードの子ノードの総数です）。簡単に言えば、各子ノードには「first」、「second」、...、「 k- th」という名前が付けられます。

バイナリツリーは（ 再帰的に ）空のセット（ノードを含まない）であるか、ノードの3つの互いに素なセットで構成されます。 ルートノード 、 左サブツリーと呼ばれるバイナリツリー、 右サブツリーと呼ばれるバイナリツリーです。したがって、バイナリツリーは、各ノードの次数が最大2で、「左」および/または「右」の子ノードを持つ順序付けられたツリーです。

完全な二分木は、各ノードが葉であるか、2のべき乗を持つ二分木です。次数1の各ノードにダミーの子シートを追加することにより、バイナリから完全なバイナリツリーを取得できます。

バイナリ検索ツリーは、バイナリツリーを通じて実装される関連データ構造であり、その各ノードは、キーと関連データ、左右のサブツリーへのリンク、および親ノードへのリンクを含むオブジェクトで表すことができます。二分探索木のキーは二分探索木の特性を満たします：

Xがノードであり、ノードYがXの左側のサブツリーにある場合、 Y.key≤X.key 。ノードYがXの右側のサブツリーにある場合、 X.key≤Y.key 。

キーを比較し（推移的な順序関係がキー値のセットで指定されている、つまり、より単純に「より少ない」操作）、キーの等価性について話すことができると理解されています。一般性を失うことのない実装では、関係に基づいて構築された操作「<」と「==」のみを使用して、厳密な順序不等式で動作します

$x = y \; \ Leftrightarrow \; \;！（x <y）\：\＆\：！（y <x）$

ツリートラバーサル-ノードのリストを形成し、順序はトラバーサルのタイプによって決まります。

ウォームアップ：タプル操作と数値をクラスに変える

再帰的な荒野に真っ向から飛び込み、山括弧の暴動を楽しむ前に、メタファンクションの作成を練習します。次に、タプル連結関数と、既存のタプルに型を追加する関数が必要です。

 template <class U, class V> struct tuple_concat; template <class Tuple, class T> struct tuple_push;

型操作について：

もちろん、「連結」や「タイプコンテナ」への「追加」の話はありません。これは、コンパイル時間の世界の一般的かつ重要な機能です。 特定の型（クラス）を変更することはすでに不可能ですが、必要なプロパティを持つ新しい（または既存の型を選択する）型を定義することは可能です。

C ++ 11標準では、便利なメタ関数のコレクションを含むtype_traits

ヘッダーファイル（タイプサポートライブラリの一部として）が導入されています。それらはすべて構造のテンプレートであり、インスタンス化後、特定のタイプのtype

または数値定数value

をローカルで定義しvalue

（または、 std::enable_if

を使用してオーバーロードを無効にする場合は何もしません）。メタファンクションを設計するという同じ原則を順守します。

最初の関数はテンプレート引数として2つのタプルを受け取り、2番目の関数はタプルとタプルに追加される型を受け入れます。不適切な型を引数として置き換える（たとえば、 int

とfloat

を連結しようとする場合）は無意味な操作であるため、これらの構造の基本的なテンプレートは定義されておらず（これにより任意の型のインスタンス化が防止されます）、すべての有用な作業は部分的な特殊化で行われます：

 template <template <class...> class T, class... Alist, class... Blist> struct tuple_concat<T<Alist...>, T<Blist...>> { using type = T<Alist..., Blist...>; }; template <template <class...> class Tuple, class... Args, class T> struct tuple_push<Tuple<Args...>,T> { using type = Tuple<Args..., T>; };

人間の言語専門分野tuple_concat

へのおおよその翻訳：

2つのクラスがテンプレート引数として機能し、同じクラステンプレート（ T

）を可変数の引数でインスタンス化した結果であり、それらがパラメーターパックAlist

およびBlist

でインスタンス化された場合、 type

エイリアスをインスタンス化としてローカルに定義します引数リストを連結した同じクラステンプレートT

バージョン、つまり T<Alist..., Blist...>

。

用語について：

さらにこの記事では、「メタ関数構造テンプレートのインスタンス化」（より正確で賢明な）および「メタ関数呼び出し」（より短く明確な）という概念がしばしば識別されますが、本質的には同じことを意味します：「プログラムのこの時点で、構造はすべての結果を持つテンプレートから生成されます結果：サイズを取得し、エイリアスとクラスが内部で定義されるなど。など。」

それは不吉に聞こえますが、実際にはすべてが見た目よりも単純です：同じタイプの2つのタプル（たとえば、2つのstd::tuple

）でtuple_concat

をtuple_concat

うとすると、入力タプルへの引数の「ステッチ」リストを持つ同じタプルのタイプが構造内で決定されます他のインスタンス化の試みは、単にコンパイルできません（コンパイラーは上記で定義された部分的な特殊化の型を推測できず、共通テンプレートのインスタンス化は本体がないため不可能です）。例：

 using t1 = std::tuple<char,int>; using t2 = std::tuple<float,double>; using t3 = std::tuple<char,int,float,double>; using conc = typename tuple_concat<t1,t2>::type; // using err = typename tuple_concat<int,bool>::type; //  static_assert(std::is_same<t3,conc>::value, ""); //  ,

上記に照らして、 tuple_push

特殊化の検討は難しくないtuple_push

です。さらに、便宜上、対応するテンプレートエイリアスを定義します。

 template <typename U, typename V> using tuple_concat_t = typename tuple_concat<U,V>::type; template <typename Tuple, typename T> using tuple_push_t = typename tuple_push<Tuple,T>::type;

この便利な機能は、C ++ 11標準の言語に登場しました。たとえば、 typename tuple_concat<t1,t2>::type

代わりにtype

にアクセスしてtypename tuple_concat<t1,t2>::type

のみを記述できます。

連結について：

標準tuple

ヘッダーには、引数として渡された未定義のstd::tuple

の数を連結してタプルを構築する（非メタ）関数tuple_cat()

の定義が含まれます。注意深い読者は、結果タイプdecltype(tuple_cat(...))

出力することでtuple_concat

をより簡単に実装できることに気付くかもしれませんが、最初に、上記で取得した実装はタプルstd::tuple

タイプに限定されず、次に、より複雑なタイプの算術演算に徐々に没入するための準備運動。

最後の準備：ビジネスのためではなく、デバッグの魂のために、整数を型に変換する方法を学びます：ツリーのノードに何かを保存する必要があります。また、通常の数字を保存するよりも簡単で便利なのは何ですか？ただし、ツリーは単純ではなく、型（およびコンパイル時間）があるため、数値は複雑でなければなりません。実際、実装は非常にシンプルで有名です。

 /// - STL-like  template<size_t number> struct num_t : std::integral_constant<size_t, number> {}; //      template<size_t number> struct num_t { enum : size_t { value = number } };

両方の定義の意味は同じです。異なる数値引数を使用してテンプレートをインスタンス化すると、さまざまなタイプの定義になります： num_t<0>

、 num_t<13>

、 num_t<42>

など。便宜上、この構造に静的な数値valueを付与しvalue

。これにより、型推論に頼らずに（ some_num_type::value

アクセスして）テンプレート引数から明示的に数値を取得できます。

バイナリ検索ツリー

バイナリ検索ツリーの再帰的な定義は、テンプレートの形で直接実装するのに便利です。簡略化された定義

  ツリー：NIL |  [ツリー、データ、ツリー]

「ツリーは空のセット、またはツリー（いわゆる左サブツリー）、データ、ツリー（いわゆる右サブツリー）の3つの要素のセット」と言い換えることができます。

さらに、すでに述べたように、バイナリ検索ツリーでは、ツリーのノードに格納されている値のセットの順序関係を指定する必要があります（何らかの方法でノードを比較および順序付けできる、つまり操作が「少ない」必要があります）。標準的なアプローチは、ノードデータをキーと値に分割することです（キーを比較し、値を保存するだけです）が、実装では、一般性を失うことなく構造を単純化するために、ノードデータを単一のタイプと見なし、順序関係を設定するために、特別なタイプのComp

（ コンパレータ 、彼についての詳細は後で）。

 ///   struct NIL {}; ///  template<typename T, typename Left, typename Right, typename Comp> struct node { using type = T; // node value using LT = Left; // left subtree using RT = Right; // right subtree using comp = Comp; // types comparator }; /// :    ( ) template <typename T, typename Comp> using leaf = node<T,NIL,NIL,Comp>;

それでもノードに格納されている型のセットで順序関係が指定されているという事実にもかかわらず、それをツリー自体に属性付けして、このツリーの型の一部として格納すると便利です：空でないツリーの検索、挿入、およびトラバースのメタ機能を呼び出す場合、追加のコンパレーターは不要です

父親と子供について：

注意深い読者は、提示された構造には、ほとんどのアルゴリズムの実装にとって重要な要素が1つ欠けているという事実に注意を払うでしょう：親ノードへのリンク（この場合、親ツリーのタイプのエイリアス）。これに気づき、この不正を修正しようとすると、読者は遅かれ早かれ恐怖に陥り、この場合は仮名の周期的な依存性があることに気づきます。

状況自体は重大ではなく、宣言と型定義の分離という形で回避策があります。

 template<...> struct one { struct two; using three = one<two, ...>; struct two : one<three, ...> {}; };

注：このような構造は、最新のgccおよびclangによってコンパイルおよびインスタンス化されることが実験的に見つかりましたが、そのような異常なテンプレートの宣言の標準への厳密な準拠をまだ確認していません。

ただし、実際には、このようなエンティティを操作して作成することは非常に困難です。親要素への逆方向リンクは興味深い効果をもたらします。実際、「単純に接続されたツリー」は実際のグラフ（おいしい！）に変わります。これは、変更を加えると、 「一度に」、完全に （悲しく）インスタンス化する必要があります。この状況のより深い分析は、この記事の範囲を超えており、C ++でのメタプログラミングの可能性を調査するための私のさらなる計画の1つです。

これは、ツリーを実装および表現する唯一の方法ではありません（たとえば、ノードをタプルに格納してインデックスを付けることができます）。しかし、このような記述は、ツリー作業アルゴリズムの直接適用にとってより視覚的で便利です。

注文関係

Comp

構造には、メタ関数の型の比較（つまり、より小さいか等しい操作パターン）が含まれている必要があります。 sizeof

型（すべての完全な型に対して定義されている唯一の数値特性）に基づいて、このような比較の例を記述しましょう。

 struct sizeof_comp { template <typename U, typename V> struct lt : std::integral_constant<bool, (sizeof(U) < sizeof(V))> {}; //  template <typename U, typename V> struct eq : std::integral_constant<bool, (sizeof(U) == sizeof(V))> {}; //  };

ここではすべてが透明である必要があります。lt-型のメタ関数は「少なく」、eq-メタ関数は「等しい」。数値のタイプを決定するために前に示したアプローチが使用されますstd::integral_constant

inherit_constantからの継承は、インスタンス化されたlt

およびeq

静的なブール値を与えます。

実際には、特定のタイプの特定のツリーに、このタスクに固有のコンパレータを提供する必要があります。たとえば、前述の「数値型」のクラスの比較を記述します。

 struct num_comp { template <typename U, typename V> struct lt : std::integral_constant<bool, (U::value < V::value)> {}; template <typename U, typename V> struct eq : std::integral_constant<bool, (U::value == V::value)> {}; };

このようなコンパレータは、一般的に言えば、普遍的であり、静的なvalue

を含む任意の型を比較できvalue

。

CRTPを介したコンパレータ生成について：

理論セクションの前半で、操作は「少ない」、一般的に言って、操作が「等しい」と直感的に判断するのに十分であると述べました。 CRTP（ 不思議な繰り返しテンプレートパターン ）に似たアプローチを使用して、操作（メタ関数）が「少ない」コンパレーターのみに基づいて完全なコンパレーターを決定します。

 ///        template <typename lt_traits> struct eq_comp { template <typename U, typename V> struct lt : std::integral_constant<bool, lt_traits::template lt<U,V>::value> {}; template <typename U, typename V> struct eq : std::integral_constant<bool, (!lt<U,V>::value && !lt<V,U>::value)> {}; }; ///   sizeof,     eq_comp::eq struct sizeof_comp : public eq_comp<sizeof_comp> { template <typename U, typename V> struct lt : std::integral_constant<bool, (sizeof(U) < sizeof(V))> {}; }; ///   num_t struct num_comp : public eq_comp<num_comp> { template <typename U, typename V> struct lt : std::integral_constant<bool, (U::value < V::value)> {}; };

定義のサイズが小さくなり、数学的な背景が現れました。完璧ではありませんか？

これで、明示的に「手で」最初のタイプツリーを定義するためのすべてができました。

 using t1 = node< num_t<5>, node< num_t<3>, leaf<num_t<2>>, leaf<num_t<4>> >, node< num_t<7>, NIL, leaf<num_t<8>> > >;

注：以下、例では、 num_comp

デフォルトで暗黙的に指定されています。テンプレート引数のリストでの明示的な指示は省略されています。一般に、 insert

操作を開発した後、この方法でツリーを構築する必要はありません（明示的な定義）。

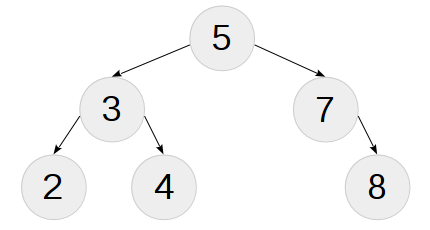
説明したツリーを図に示します。

コンパイル時のデバッグについて：

定義したクラスが意図したものを正確に記述していることをどのように確認しますか？

議論と研究のためのこの別個の興味深いトピックは、メタプログラムのデバッグです。呼び出しスタック、変数、いまいましいprintf/std::cout

はありません。コンパイラエラーメッセージ内に人間が読み取れる推定型を出力できる手法がありますが、原則として、これは生成された構造をチェックするのにかなり役立つ機能です（たとえば、ツリーを変更した後）。

単に誤ったプログラムの場合は、マルチメガバイトのエラーメッセージの問題に触れません：練習後、これは問題ではなくなります。ほとんどの場合、インスタンス化の最初のエラーのみがさらなるエラーのカスケードにつながるためです。

しかし、逆説的に聞こえるかもしれませんが、プログラムが正常にコンパイルされたらどうでしょうか？ここで、著者はデバッグ方法の選択においてすでに自由です。 type_traits

定義されているようなメタ関数の結果の型は、 typeid(t).name()

として単純にtype_traits

できます（C ++ 11以降、合法的にRTTIをスパイできます）。単純なデータ構造は、末尾再帰を備えた特別なメタ関数を使用して画面に表示できます。複雑な構造の場合、構造自体の操作と「プリンター」の複雑さを同等にする必要があります。

ツリーライブラリにはこのようなプリンタとその使用例が含まれており、読者は記事の最後にあるgithubへのリンクでそれらに慣れることができます。たとえば、上記の例の印刷されたツリー：

                   /-{2}  
          /-{3}-<
                   \-{4}  
 -{5} --- <
          \-{7}-\
                   \-{8}

身長

二分木の高さを計算するための再帰関数を見てみましょう：

  ///入力：T-ツリー、出力：h-高さ

 
  高さ（T）： 
      IF T == NIL 
          結論0 
      その他 
          出力1 +最大（高さ（T.LEFT）、高さ（T.RIGHT））

彼女は美しい。この関数をC ++に移植して移植するだけです。

 ///    template <typename Tree> struct height; ///  : " T == NIL" template <> struct height<NIL> : std::integral_constant<size_t, 0> {}; ///    () template <typename Tree> struct height { static constexpr size_t value = 1 + max( height<typename Tree::LT>::value, height<typename Tree::RT>::value ); };

注：計算されたツリーの高さは、数学的な定義よりも1大きくなります（空のセットの高さは定義されていません）。 , 1 , height

.

コードは非常に簡単です：height

空のセットで呼び出すと、対応するstaticを含む特殊化がインスタンス化されますvalue = 0

。そうでない場合、インスタンス化のカスケードは、NIL

再帰が停止する空のサブツリー（つまり、同じサブツリー）に出会うまで続きます。これは、C ++テンプレートを介して再帰関数を実装する際の特徴的な機能です。再帰bottomを特殊化する必要があります。特殊化ある時点で上記の関数を取得できないTree::LT

場合Tree

空のサブツリーと等しくなりますNIL

）。

上記のコードは関数を使用していますmax

。それはする必要がありconstexpr

、シンプルでよく知られている実装の例（またはメタ機能、そして少し変更それを呼び出します）：

 template <typename T> constexpr T max(T a, T b) { return a < b ? b : a; }

最後に、関数を使用しますheight

：

 static_assert(height<t1>::value == 3, "");

関数の「複雑さ」について話しましょう。n個のインスタンス化がheight

必要です。nはツリーノードの数です。インスタンス化の深さはh-つまり木の高さ。

これ以上に複雑で、なぜここにあるのですか？！

, , , : (!), - , . , : , constexpr

- variadic- .

: , gcc-5.4 « » ( ) 900 . , ( ). , height

gcc, > 900. O - ( ), .

, C++14 ( std::integer_sequence

): N 0..N-1, , . , , ( , 30- 9000- ).

, (.. ) : . ( , ..), , — , — API , , — ( « 24 »!).

バイパス中心（インオーダートラバーサル）

回避策は、特定の方法でノード（またはノードからのデータ）のリストを作成することです。これは、実際に重要な用語の問題です）。中央（対称）トラバーサルは、左右のサブツリーの対応するトラバーサルの結果の間でツリーのルートが発生するトラバーサルです。一緒に二分探索木の特性は、それは、二分探索木の周りを中心に、我々が生成することを言います（。不平等にし、理論を参照）、ノードのソートされたリストクールを- ！以前に定義されたツリーのトラバースは次のようになります。

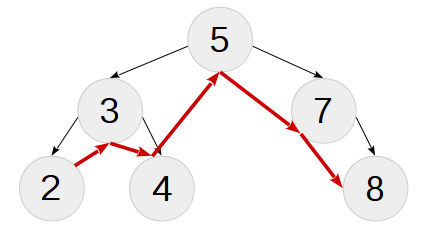
再帰的な回避アルゴリズムは非常に簡単です。

 ///入力：T-ツリー、出力：w-ノードのデータを順番にトラバースするリスト

 
順序（T）：
    IF T == NIL
        結論{}
    その他
        出力順（T.LEFT）+ {T.KEY} + INORDER（T.RIGHT）

この場合の操作「+」は、リストの連結を意味します。はい、タプルはコンパイル時に型リストであるため、タプルを連結するために使用したものです。そして再び-コードを取得して記述します。

 ///    template <typename Tree> struct walk; ///  : " T == NIL" template <> struct walk<NIL> { using type = std::tuple<>; }; ///    () template <typename Tree> struct walk { private: //    using accL = typename walk<typename Tree::LT>::type; //   using accX = tuple_push_t<accL, typename Tree::type>; //      using accR = tuple_concat_t<accX, typename walk<typename Tree::RT>::type>; public: //  using type = accR; };

この場合、明確にするためだけに、ローカルprivate

エイリアスを使用しました。すべてのエイリアスを相互に置き換えて、ランダムに生成された行の後にスタッフィングを難読化することができ、インデントでさえも保存されません。しかし、私たちは人々のために努力しますよね？

関数の複雑さwalk

はO（n）インスタンス化です。ここで、nはツリーノードの数です（O表記は簡略化に使用されます。正確なカウントでは、連結を考慮して約3nのメタ関数呼び出しが行われます）。機能することをそれのnice tuple_concat

とtuple_push

1つのインスタンス化のために自分の仕事を行って、彼らは再帰的ではありませんので、（タイプの可能性の撤退に伴うparameter pack

さん）。例のように、インスタンス化の深さはhにheight

等しい -木の高さ。

コードの可読性について：

: , , .

: , , , . , : « ». , : , .

検索する

キー検索は、古典的なバイナリ検索ツリーの主な操作です（名前はそれ自体を表しています）。キーとデータを分離しないことに決めたので、導入された比較器を使用してノードを比較しComp

ます。再帰的検索アルゴリズム：

 ///入力：T-ツリー、k-キータイプ、
///出力：N-比較に関してタイプk` == kを含むノード

 
検索（T、k）：
    T == NILまたはk == T.KEYの場合
        結論T
    その他
        IF k <T.KEY
            出力検索（T.LEFT、k）
        その他
            結論の検索（T.RIGHT、k）

実装は、以前に開発された実装に似ています。

 ///    template <typename Tree, typename T> struct search; ///     template <typename T> struct search<NIL,T> { using type = NIL; }; ///    template <typename Tree, typename T> struct search { using Comp = typename Tree::comp; using type = typename std::conditional< Comp::template eq<T, typename Tree::type>::value, // k == T.KEY ? Tree, //  , : typename std::conditional< Comp::template lt<T, typename Tree::type>::value, // k < T.KEY ? typename search<typename Tree::LT, T>::type, //     typename search<typename Tree::RT, T>::type //  --   >::type >::type; };

それはもう少し複雑に見えますが、偶然ではありません：まず、アルゴリズム自体がより多くのブランチ（より多くの比較と条件）を含んでいます、次に、先に定義した順序関係を適用し、それに基づいて、左または右サブツリー。詳細に注意してください：

型を比較するには、ツリーのルートからコンパレータを使用します：Tree::comp

論理的です：順序関係は、ツリーの構築方法と後続の操作（検索を含む）の両方を決定するため、コンパレータのエイリアスをツリーテンプレート（node<>

）内に直接配置するのが便利でした。
アクセスするにはテンプレート依存テンプレート引数を（Tree::comp::eq<...>

とTree::comp::lt<...>

）は、キーワードを使用する必要がありますtemplate

。
std::conditional

— , ( ?: ). — . , — .

そのようなインプリメンテーションの複雑search

再度- O（n）のインスタンス、深さ- 時間（木の高さ）。「やめて！」と驚いた読者は「検索の対数的複雑さなどはどうだろう？」と叫ぶと

、石が横に飛んでstd::conditional

、演算子との根本的な違いが明らかになりますか？ ::三項演算子は評価されない式を評価しませんその結果（たとえば、良心で、演算子の最初の引数でこのポインターをチェックするときに破棄される2つの式のいずれかでnullポインターを逆参照できます）。std::conditional

また、すべての3つの引数をインスタンス化する理由は一つだけである（通常のメタ関数など）を、std::conditional

再帰を停止するのに十分ではなく、再帰の底を特殊化する必要があります。

直接の結果は、根から葉までツリー全体をキャプチャする余分なインスタンス化です。特別なソーサリーでは、別のレベルの間接化を追加して、未知のノードがまったくないサブツリーのパスに沿ったインスタンス化の再帰の各ステップで「オフ」にし（このレベルの間接化に特化した束を作成することにより）、しかし、O（h）の大切な複雑さを達成できます私の意見では、これはより深い研究のためのタスクであり、この場合は時期尚早な最適化になります。

アプリケーションの例（使用されたエイリアステンプレート。他の例についてはリポジトリを参照）：

 using found3 = search_t<NIL, num_t<0>, num_comp>; //    using found4 = search_t<t1, num_t<5>, num_comp>; //    using found5 = search_t<t1, num_t<8>, num_comp>; //    static_assert(std::is_same<found3, NIL>::value, ""); //   static_assert(std::is_same<found4, t1>::value, ""); //   static_assert(std::is_same<found5, leaf<num_t<8>>>::value, ""); //

これは奇妙に思えるかもしれません：私たちは、実際に引数として既に指定されているタイプのノードを探しています-なぜですか？実際、これには珍しいことは何もありません- 比較の観点から引数に等しい型を探しています。 STLは（木std::map

）ものノードに格納されているペア（std::pair

）、及び一対の第一部材があると考えられているキー実際には、比較に関与します。ツリーに同じものを保存し、比較器にペアの最初のタイプのペアをstd::pair

比較させるだけで十分ですComp

-そして、古典的な連想（メタ）コンテナを取得します！記事の最後でこの考えに戻ります。

挿入

メタ機能の助けを借りてツリーを構築する方法を学ぶときです（以前と同じように、手でツリーを描くことはすべて完了していませんか？）。再帰挿入アルゴリズムは、新しいツリーを作成します。

 ///入力：T-ツリー、k-挿入するキータイプ、
///出力：T '-要素が挿入された新しいツリー

 
INSERT（T、k）：
    IF T == NIL
        結論{NIL、k、NIL}
    その他
        IF k <T.KEY
            結論{挿入（T.LEFT、k）、T.KEY、T.RIGHT}
        その他
            結論{T.LEFT、T.KEY、INSERT（T.RIGHT、k）}

彼の仕事を説明しましょう：挿入が発生するツリーが空の場合、挿入された要素は新しいツリー{NIL、k、NIL}を作成します。この要素を持つシート（再帰下部）。ツリーが空でない場合、空のツリーに再帰的に失敗し（つまり、左または右のサブツリーが空になるまで）、最後にこのサブツリーで同じシート{NIL、k、NIL}を形成する必要がありますNIL、新しい左または右のサブツリーの形で「ハング」する途中。型の世界では、既存の型を変更することはできませんが、新しい型を作成することはできます-これは再帰のすべてのステップで発生します。実装：

 template <typename Tree, typename T, typename Comp = typename Tree::comp> struct insert; ///   template <typename T, typename Comp> struct insert<NIL,T,Comp> { using type = leaf<T,Comp>; }; ///   template <typename Tree, typename T, typename Comp> struct insert { using type = typename std::conditional< Comp::template lt<T, typename Tree::type>::value, // k < T.KEY? node<typename Tree::type, //   {INSERT(T.LEFT,k), T.KEY, T.RIGHT} typename insert<typename Tree::LT, T, Comp>::type, typename Tree::RT, Comp>, node<typename Tree::type, //   {T.LEFT, T.KEY, INSERT(T.RIGHT,k)} typename Tree::LT, typename insert<typename Tree::RT, T, Comp>::type, Comp> >::type; };

空のツリーに要素を追加するには、コンパレーターを明示的に指定する必要がありますComp

。ツリーが空でない場合、コンパレータはデフォルトでこのツリーのルートから取得されます*。

この挿入の複雑さは次のとおりです。O（n）インスタンス化（nは既存のノードの数）、再帰の深さはh（hはツリーの高さ）です。明示的な使用例：

 using t2 = leaf<num_t<5>, num_comp>; using t3 = insert_t<t2, num_t<3>>; using t4 = insert_t<t3, num_t<7>>; static_assert(height<t4>::value == 2, ""); //  2  using t5 = insert_t<insert_t<insert_t<t4, num_t<2>>, num_t<4>>, num_t<8>>; static_assert(std::is_same<t5, t1>::value, ""); //

ライブラリにはメタinsert_tuple

タイプの実装があり、これにより、タイプのタプルをすぐにツリーに入れることができます（ボンネットの下ではinsert

、タプルの単なる再帰です）。

 using t6 = insert_tuple_t<NIL, std::tuple< num_t<5>, num_t<7>, num_t<3>, num_t<4>, num_t<2>, num_t<8> >, num_comp>; static_assert(std::is_same<t1, t6>::value, "");

バイパス幅（幅優先トラバーサル）

二分木の幅を横断する（またはグラフ理論から幅を探索する）と、ノードのリストが「レベル」順に表示されます。最初にルート、次に深さ1のノード、次に深さ2のノードなどが表示されます。このようなバイパスのアルゴリズムは、スタックではなくノードのキューを使用してさらに出力するため、再帰的に「変換」することは困難です。ネタバレの下で、興味のある読者は回避策を見つけるでしょう。ここでは、幅をクロールすることで「解析」されたツリーを、クロール結果のタプルから要素のまったく同じシーケンシャル挿入にアセンブルできるという有用な事実のみに注目します。この図は、テストツリーの幅の周りを歩いています。

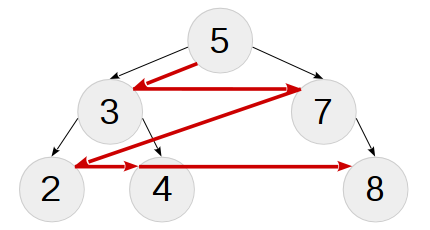
再帰的な幅のウォーク：

: 0 h . :

 /// : T - , l -   ,
/// : t -

COLLECT_LEVEL(T,l):
     T == NIL
         {}
    
         l == 0
             {T.KEY}
        
             COLLECT_LEVEL(T.LEFT,l-1) + COLLECT_LEVEL(T.RIGHT,l-1)

. , O(nh) - (, , collect_level

).

取り外し？

ノードの削除は重要なタスクです。古典的なアプローチでは、3つのケース（子ノードの数による）が考慮され、後続ノードと親ノードの概念がアルゴリズムで使用されます。親ノードへのバックリンクがない場合（「父親と子供について」のネタバレ参照）、アルゴリズムを効果的に実装するのは問題です。ツリーを登る各操作にはO（n）の複雑さがあります。このような削除の単純な実装は、インスタンスの数の点で「組み合わせの爆発」を引き起こします（複雑さはO（n ⁿ）付近です）。ノードを削除するためのメタ関数の開発は、ライブラリを改善するためのさらなる計画の一部です。記事の最後にあるUPD2を参照してください。

申込み

息を吸って、最後に質問に注意を払いましょう。なぜバイナリコンパイル時の検索ツリーが必要なのでしょうか？3つの答えがあります：

非建設的：

*トロリーバスのある写真*。省略します。

明らか：

...研究に興味のある人向け

構成的：

この構造の可能なアプリケーションの例を次に示します。

: , . «» . — ( — O(n ² ) ), — .
runtime : , -. std::tuple

— . , runtime , , ( std::get

std::tuple

).
compile-time: std::map

( std::set

) — , (, ) ( — , ..), compile-time, runtime . : , , . : ?
: « », . , , , .

«Modern C++ Design: Generic Programming and Design Patterns Applied» ( « ++» , . ) : « ». static_assert

, C++11, ( , policy ), STL, C++98 (« ») ( , , , ).

, : compile-time — , ( , ), ( «», , - ).

締めくくりに、ツリーの開発と記事の執筆につながったタスクについて、少しお話したいと思います。正規表現をDFA（決定論的有限状態機械）に直接変換するためのアルゴリズムがいくつかあり、それを認識します。そのいくつかは、いわゆる 構文ツリー、その性質上、「何もない」バイナリです。したがって、コンパイル時検索のバイナリツリーは、（コンパイルおよびDFAのフラットコードに展開できる埋め込み後の）正規表現のコンパイル時パーサーの不可欠な部分（および実装のための単なる興味深い構造）であり、これは別のプロジェクトの一部になります。

それで何？

ささやき：冬...

, (, , ) . — , (, - ), std

- ( — tutorial ). , .

!

文学

, ., , ., , ., , . : = Introduction to Algorithms. — 2-. — .: , 2005. — 1296 .
. ++: = Modern C++ Design: Generic Programming and Design Patterns Applied. — . .: , 2008. — 336 . — (++ in Depth).
., . ++. «C++ In-Depth» = C++ Coding Standards: 101 Rules, Guidelines and Best Practices (C++ In-Depth). — .: «», 2014. — 224 .
. C++ , . «C++ In-Depth» = Discovering Modern C++: A Concise Introduction for Scientists and Engineers (C++ In-Depth). — .: «», 2016. — 512 .

→ リポジトリ

UPD：

std::conditional:

izvolov std::conditional

. search

O(h) :

 template <typename Node, typename T, typename Comp> struct search { using type = typename std::conditional< Comp::template eq<T, typename Node::type>::value, Node, typename search<typename std::conditional< Comp::template lt<T, typename Node::type>::value, typename Node::LT, typename Node::RT >::type, T, Comp>::type >::type; };

(+ insert

) .

UPD2：

remove insert search O(h):

, insert

search

remove

O(h) ( insert

). SFINAE + decltype

( , . ). remove

:

 template <typename Tree, typename T> struct remove { private: enum : bool { is_less = Tree::comp::template lt<T, typename Tree::type>::value }; enum : bool { is_equal = Tree::comp::template eq<T, typename Tree::type>::value }; enum : size_t { children = children_amount<Tree>::value }; using key = typename min_node_t< typename std::conditional< is_equal && children == 2, typename Tree::RT, leaf<typename Tree::type, typename Tree::comp> >::type >::type; using recursive_call = typename remove< typename std::conditional< is_less, typename Tree::LT, typename std::conditional< !is_equal || children == 2, typename Tree::RT, NIL >::type >::type, typename std::conditional< is_equal, key, T >::type >::type; static typename Tree::RT root_dispatcher(...); template <typename Bush> static typename std::enable_if< sizeof(typename Bush::LT::type), typename Bush::LT >::type root_dispatcher(Bush&&); public: using type = typename std::conditional< is_equal && (children < 2), decltype(root_dispatcher(std::declval<Tree>())), node< key, typename std::conditional< is_less, recursive_call, typename Tree::LT >::type, typename std::conditional< !is_less, recursive_call, typename Tree::RT >::type, typename Tree::comp > >::type; };

, , . , , , , .

C ++メタプログラミングの実践：コンパイル時のバイナリ検索ツリー

内容