
以下では、老婦人の再帰についてお話します。
注:この短い記事は、再帰の簡単な紹介、その使用例、および危険のために書かれています。
定義
まず第一に、再帰はプログラミングだけではないことを言う価値があります。 再帰は、あらゆるものに固有であり、日常生活で見られる一般的な概念ですが、コンピューターサイエンスと数学では最も一般的です。 プログラマーにとって、再帰を使用する能力は、有用なスキルのコレクションにおいて大きなプラスです。
最大の愚かさは同じことをし、別の結果を期待することです。
再帰とは、自己相似の方法で要素を繰り返すプロセスを意味します。 オブジェクトは、それ自体の一部である場合、再帰を持ちます。
再帰の特殊なケースは末尾再帰です。 再帰呼び出しが関数から戻る前の最後の操作である場合、これがそれです。
いくつかの例
再帰を理解する必要があり、この定義は説明的な例よりも悪いです。 もちろん、理解を深めるために、定義を読み、例を見て、定義をもう一度読んで、もう一度例を見てください。認識が来るまで繰り返します。
ここで素晴らしい例を見つけることができます。
プログラマーにとって最も有名な再帰の使用法は、フィボナッチ数または階乗を計算するタスクです。 Cでこれを実装する方法を示しましょう。
int fib(int n) { if (n == 0) return 0; if (n == 1 || n == 2) return 1; return fib(n - 1) + fib(n - 2); }
fib(1,1):-!. fib(2,1):-!. fib(N,R):- N1 is N-1, fib(N1, R1), N2 is N-2, fib(N2, R2), R is R1 + R2.
宣言的パラダイム、特に論理プログラミングパラダイムは、再帰を理解するのを一般的によくしているため、すぐに注目に値します。
int factorial_rec(int n, int res) { if (n == 0) return res; return factorial_rec(n - 1, res * n); } int factorial(int n) { return factorial_rec(n, 1); }
フォークボム
注:再帰的なプロセスの作成は(その数が指数関数的に増加するため)非常に迅速にプロセステーブルをいっぱいにしますが、これはシステムにとって非常に危険です。
#include <unistd.h> int main() { while(true) fork(); }
これを行った後にボタンで再起動するのは少し良くありません。
数学者にとって、最初の関連付けはフラクタルになる可能性があります。 フラクタルは美しく、目に心地よく、自己相似の特性を示します。
最も有名なフラクタル:
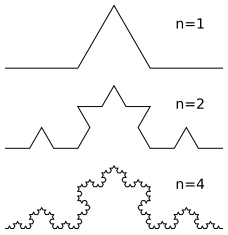


さて、日常生活では、向かい合って設置された2つのミラーが典型的な例です。
もっと深く

再帰は簡単ですか? 絶対にありません。 すべてが単純であるように思われますが、再帰には危険が伴います(そして、時にはそれが明確ではありません)。
フィボナッチ数の計算の例に戻りましょう。 関数の戻り結果は、同じ関数の呼び出し、より正確には、2つの関数の呼び出しの結果の合計であることに注意してください(これが再帰が末尾ではない理由です)。 2番目の呼び出しは、最初の呼び出しが完了するまで行われないことが明らかになります(最初の呼び出しでは、 2つの関数の呼び出しも行われます)。 探究心は、自己呼び出しなしで再帰関数から抜け出す「通常の」方法があることにすぐに気付くでしょう。そうでなければ、呼び出しスタックのオーバーフローを知ることができます-これは、自分自身を呼び出す関数で作業するときに留意すべき重要なポイントの1つです。
コールツリーは大きくなりますが、スタック内のコールの最大数は著しく少なくなります(それぞれN> 2の場合はN-1)。

再帰アルゴリズムは、ツリー、ソート、グラフのタスクを操作する際に非常に一般的です。 したがって、よりよく理解するために、前述のことはこれにとって悪いことではありません(特にバイナリツリーまたは共通ツリー。それらの実装はそれほど複雑ではなく、再帰の経験は悪くありません)。
さらに、 ハノイの塔についても言及したいと思います。これは、再帰的なタスクに慣れるのにも優れています。 Habréでも、このゲームの優れた分析がありました。
絵を完成させるためには、再帰との戦いに言及する必要があります。
なぜそれと戦うのですか?
生産性の向上。 しかし、これは、反復オプションよりも再帰の使用がより明白で単純で快適なため、単に対処する必要があるという意味ではありません。
再帰を克服できますか?
間違いなくはい。 再帰アルゴリズムは、再帰を使用せずに書き換えることができますが、末尾再帰は反復に変換するのが非常に簡単です(一部のコンパイラは最適化のために行います)。 これは、反復アルゴリズムにも適用されます。
最もよく知られている方法は、スタックを使用することです。 興味のある方はこちらをご覧ください。
おわりに
記事を読んでくれてありがとう。 再帰に慣れていない人の大部分がそれについての基本的なアイデアを得て、もちろん、知識のある人からは、コメントに追加やコメントを聞きたいと思っています。 再帰を恐れず、スタックをオーバーフローさせないでください!
UPD:末尾再帰の正しい例を追加しました。