👱🏿 🐈 👷🏼 なじみのある顔を探して 🔕 ⏳ 🌇

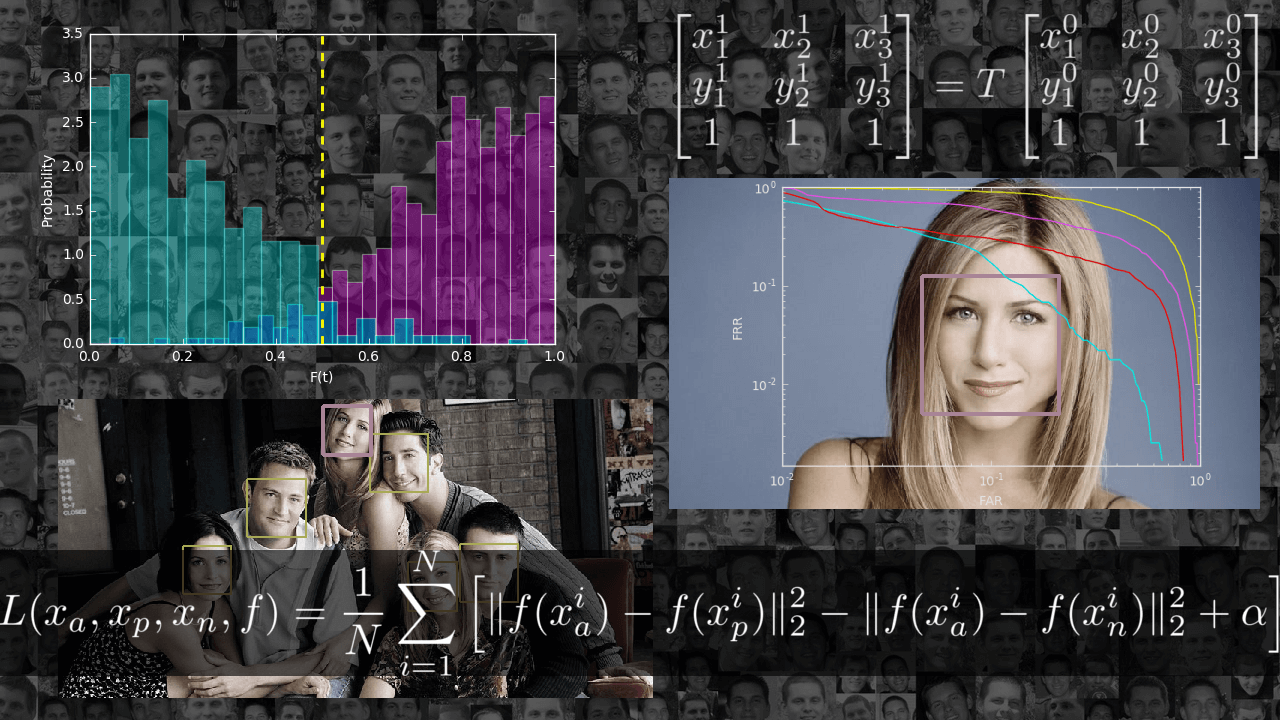
この記事では、読者に識別のタスクを紹介します。基本的な定義から、この分野の最近の記事の1つを実装することです。結果は、写真で同じ人を検索できるアプリケーションであり、最も重要なのは、その仕組みを理解することです。

Bourneの識別（Bourneだけでなく）

識別問題は分類問題に似ており、歴史的にその問題から生じました。オブジェクトのクラスを決定する代わりに、オブジェクトに必要なプロパティがあるかどうかを決定することが必要になりました。識別問題では、トレーニングセットはオブジェクトのセットです $M = \ {x_i \} _ {i = 1} ^ n$ 、それぞれにプロパティがあります $A$ ： $A（x_i）= 1、\; i = \上線{1、n}$ かどうか。さらに、すべてのオブジェクトは同じクラスに属し、指定されたプロパティを持たないオブジェクトの代表的な選択を行うことは不可能です $A$ 。

たとえば、サルの顔から人の顔を分離する場合、これは分類タスクです。2つのクラスがあり、オブジェクトごとにクラスを指定して、両方のクラスの代表的なサンプルを作成できます。顔画像がどの人物に属するかを決定する必要があり、これらの人物が有限の固定セットである場合、これも分類タスクです。

今、あなたが彼の顔の写真から人を決定するアプリケーションを開発しており、データベースに記憶されている多くの人々が絶えず変化していることを想像してください。当然、使用中、アプリケーションはトレーニングセットにいない人を見るでしょう-実際のタスク現代世界は誰も驚かないでしょう。ただし、分類の問題ではなくなりました。解決方法は？

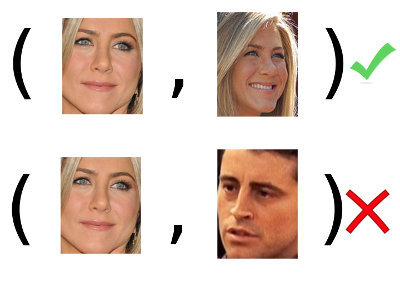
人を認識できるようにするには、少なくとも一度は会う必要があります。より正確には、少なくとも彼の写真を1枚持っているか、特定の画像の形でそれを覚えている。その後、彼らがこれまで知られていない新しい写真を見せたら、それをすべての記憶された画像と比較し、答えを出すことができます：私たちはすでにこの人を見て、彼または私たちが会ったことがないこの人を識別でき、彼だけを覚えることができます。したがって、上記の問題は次のようになります。2枚の写真を持つ $（p_1、\; p_2）$ それらが1人に関係するかどうかを判断します。言い換えれば、彼らは一人に属するという特性を持っていますか？

$A（p_1、\; p_2）= \ begin {cases} 1＆amp; \ text {、} p_1 \ text {and} p_2 \ text {belong to person person} \\ 0＆amp; \ text {、それ以外の場合} \ end {ケース}$

識別問題の定義は次のとおりです。トレーニングサンプルによる（例では、顔の多くのペア $M = \ {（p_i、p_j）\} _ {i、j = 1} ^ n$ ）ビルド識別子 $F：R ^ n \から\ {0、1 \}$ 、オブジェクトに必須属性があるかどうかを判断できます。しかし、離散性は退屈です。サインの重大度を知ることははるかに興味深いです $A$ 確率に等しいオブジェクト $p \ big（A（x）= 1 \ vert x \ big）\ R$ 。

この例の最後の問題は、 arxiv.org 、 Python 、およびKerasの助けを求めることで、もう少し形式的かつ英雄的に解決します。顔写真-からの行列 $R ^ {m \ times n}$ 。 2人の場合、1人に属する確率を知りたいです。確率は0〜1の実数です。したがって、関数を探しています。 $F：R ^ {m \ times n} \ times R ^ {m \ times n} \から[0; 1]$ 。ヤードは既に2017年であるため、機械学習法を使用して検索します。ただし、トレーニングセットには、定義からのペアは多くありませんが、分類タスクの場合と同じように、ラベルを持つさまざまな人の顔の写真がたくさんあります。これらのセットは同等ですが、2番目のセットは操作が簡単です。

ボーンスプレマシー

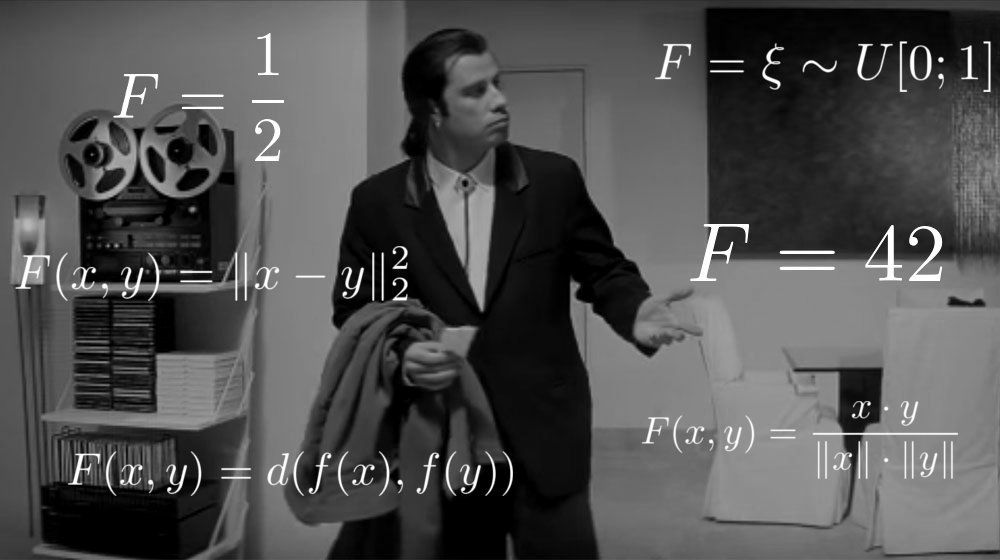
機械学習の問題を解決する上で最も重要なことは何ですか？答えを探す能力があると思いますか？いいえ、主なことはこの答えを検証する能力です。機能 $F（x、y）= \ xi \ sim U [0; 1]$ 間隔から乱数を返す $[0; 1]$ は問題に対する完全に正しい解決策ですが、実際には役に立たない。「目で見る」方法に頼らずに調べる方法は？分類問題では、検証セットの正確さ、つまり正しく分類された例の割合を見ることができます。識別の問題については、このようなメトリックは適用されません。では、問題解決の適性を客観的に評価するにはどうすればいいのでしょうか？

ターゲット試行と偽者試行の概念を紹介しましょう。最初にオブジェクトを呼び出します $Xのx \$ そのために知られている $p \ big（A（x）= 1 \ vert x \ big）= 1$ 、つまりオブジェクトには、確率1の必須プロパティがあります（この問題では、1組の面 $（p_1、p_2）$ 1人に属する）、2人目はそれぞれオブジェクト $Xのx \$ そのような $p \ big（A（x）= 1 \ vert x \ big）= 0$ 。したがって、我々はセットを考慮します $T = \ {x \ in X \ big \ vert p \ big（A（x）= 1 \ vert x \ big）= 1 \}$ そして $I = \ {x \ in X \ big \ vert p \ big（A（x）= 1 \ vert x \ big）= 0 \}$ 検証セットになります： $T \カップI = \上線{M}$ 。機械学習タスクに関しては、彼の選択の考慮事項は絶対に標準です-それは代表的なものでなければなりません。必要なすべての可変性を反映し、十分なサイズである。たとえば、顔認識システムにさまざまな照明条件での作業が含まれる場合、これらの条件は検証セットで（もちろんトレーニングセットでも）提示する必要があります。

構築された関数を取ります $F$ そしてビルド $F（T）= \ {F（t）\ vert t \ in T \}$ -申請結果 $F$ すべてのターゲット試行に対して。間隔から実数のセットを取得します $[0; 1]$ またはスコア 。これらの値は、彼らがそれをだまそうとせず、それから肯定的な答えを期待していない場合に、私たちのソリューションがどれだけうまく機能するかの尺度です。さらに $F（t）$ -代表とみなされるサンプル。その経験的密度-ヒストグラムを構築しましょう。

彼女は探します $F（x、y）= \ xi \ sim U [0; 1]$ ：

同意して、そのような識別子にはほとんど意味がありません-半分の場合は答えを推測し、半分は間違っています。

そのような分布はすでに私たちに適しています：

ターゲットの試みの場合、そのような関数はそうでないよりも正確であることをより確実にします。

しかし、詐欺師を配布せずにターゲットの配布を考慮することは無意味です。それらに対して同じ操作を実行します：分布密度を構築します $F（i）$ 同じグラフに表示します。同様の画像が得られます。

詐欺的な試みの場合、ほとんどの場合、私たちの機能は正しい答えに傾いていることが明らかになります。しかし、これらはまだ視覚的な観察にすぎず、 客観的な評価を与えるものではありません。

システムが入力で画像のペアを受け取ると仮定します。彼女は彼らのためにこれが標的の試みである可能性を計算できます。しかし、彼女には明確な答えが必要です。それは同じ人物であるかどうか、彼を秘密のオブジェクトに入れるかどうかです。しきい値を設定しましょう $d \ in [0; 1]$ そして $F（t）＆lt; d$ 、否定で答えます。それ以外の場合は肯定で答えます。もし $d = 0$ 、システムは誰も認識せず、 $d = 1$ 、その後、任意の2人が同じと見なされます。グラフは、分布が分離可能ではなく、選択できないことを示しています $d$ 両方のケースで完璧なパフォーマンスを達成するために。たとえば、上記の例で設定した場合、どうなりますか $d = 0.5$ ？

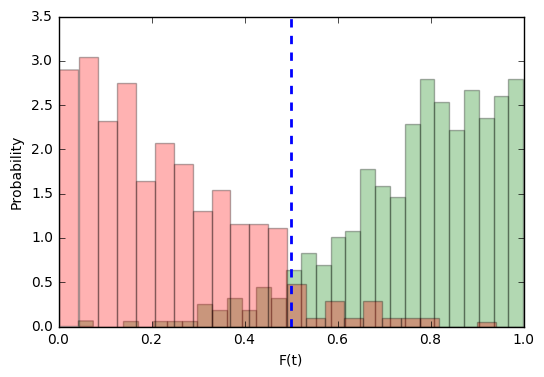
ターゲットの試行中にシステムがミスをするケースはいくつありますか？数えやすい： $\ big \ vert \ {x \ in F（T）\ vert x＆lt; d \} \ big \ vert$ -不正な試行として誤って分類されるターゲット試行の数。後者についても同様です。次に、名前を付けて、絶対ではなく相対的な名前にします。

$FRR = \ frac {\ big \ vert \ {x \ in F（T）\ vert x＆lt; d \} \ big \ vert} {\ big \ vert F（T）\ big \ vert}$

$FAR = \ frac {\ big \ vert \ {x \ in F（I）\ vert x＆gt; d \} \ big \ vert} {\ big \ vert F（I）\ big \ vert}$

FRR （False Rejection Rate）-誤って拒否されたターゲット試行の割合。
FAR （False Acceptance Rate）-不適切に受信された詐欺の試みの割合。

一歩踏み出しましょう $\ Delta d = \ frac {1} {N}$ そして、それに対してFRRとFARの値を計算します $N$ 間隔からのポイント $[0; 1]$ そしてそれらを1つのチャートに表示します：

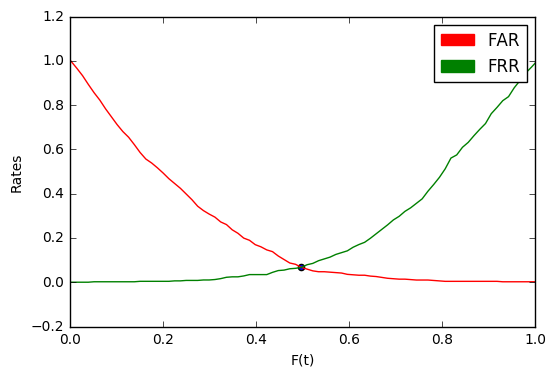
ここで、選択された距離について、 ターゲットの試行のどの割合が拒否され、どの程度の詐欺の試行が受け入れられるかを言うことができます。そしてその逆に、あなたは選ぶことができます $d$ タスクに基づいて。例えば、見知らぬ人を逃さないことが重要である保護されたオブジェクトでの検証には、明らかな理由で、それが必要です $d$ 可能な限り低いFARを提供します。コンピューターがあなたを認識し、おはようを望み、あなただけが通常アパートを回る場合は、低FRRと十分に高いFARで停止できます。コンピューターが彼にあなたの名前を呼んで誰かに挨拶しても悪いことは起こりません。

グラフの交点に注意してください。その中の値はEER （Equal Error Rate）と呼ばれます。

$EER = \ arg \ min_ {FAR} \ big \ vert FAR-FRR \ big \ vert$

選択した場合 $d = d_ {eer}$ 、 FARとFRRの値は等しいです。 EERは、私たちが行った非常に客観的な基準です。これにより、識別の品質全体を評価できます。これは、検証セットの平均誤差です。固定FRRでFARを見ることができ、その逆も可能ですが、ほとんどの場合、メトリックとして使用されるのはEERです。

上記の例では、 EER = 0.067です。これは、すべての標的の試みの平均6.7％が拒否され、すべての偽者の試みの6.7％が受け入れられることを意味します。

もう1つの重要な概念はDET曲線です。対数スケールでのFRRのFRRへの依存性です。その形式によって、システム全体の品質を判断し、1つの基準の値を一定の秒で取得できることを評価し、最も重要なことには、システムを比較するのが簡単です。

ここでのERRは、 DET曲線と直線の交差点です。 $y = x$ 。

Pythonでの素朴な実装（ FARとFRRが次の点でのみ変化すると考えると、より最適な場合があります $F（T）\カップF（I）$ ）：

import numpy as np def calc_metrics(targets_scores, imposter_scores): min_score = np.minimum(np.min(targets_scores), np.min(imposter_scores)) max_score = np.maximum(np.max(targets_scores), np.max(imposter_scores)) n_tars = len(targets_scores) n_imps = len(imposter_scores) N = 100 fars = np.zeros((N,)) frrs = np.zeros((N,)) dists = np.zeros((N,)) mink = float('inf') eer = 0 for i, dist in enumerate(np.linspace(min_score, max_score, N)): far = len(np.where(imposter_scores > dist)[0]) / n_imps frr = len(np.where(targets_scores < dist)[0]) / n_tars fars[i] = far frrs[i] = frr dists[i] = dist k = np.abs(far - frr) if k < mink: mink = k eer = (far + frr) / 2 return eer, fars, frrs, dists

コントロールを見つけました：今、どんな機能でも $F$ 選択していませんが、検証セットでFAR 、 FRR 、 ERRを計算し、視覚的なグラフを作成できます。

重要：識別の問題では、上記の検証セットと呼ばれるものを開発セット （開発セット、devset）と呼びます。将来、この表記法を順守します。

重要：実軸の間隔は $R$ セグメントに表示できます $[0; 1]$ 、関数の値がゼロから1の範囲にあることは絶対に必要ではありません。単一のセグメントに表示しなくても、結果に影響を与えることなく値の範囲を考慮することができます。

ベース準備

多くの顔認識データセットがあります。一部は有料で、一部はリクエストに応じて利用できます。照明に大きなばらつきがあるものもあれば、顔の位置にあるものもあります。いくつかは実験室で撮影されたもので、他は自然の生息地で撮影された写真から編集されたものです。データ要件を明確に定式化すると、適切なデータセットを簡単に選択したり、複数のデータセットから組み立てたりできます。私にとって、この教育タスクのフレームワーク内での要件は次のとおりでした。データセットはダウンロードのために簡単にアクセスでき、あまり多くのデータを含まず、顔の位置に変動性を含む必要があります。私が1つに結合した3つのデータセットは、要件を満たしました。

それらはすべて古くなっており、高品質の最新の顔認識システムを構築することはできませんが、トレーニングには理想的です。

このようにして得られたデータベースは、277人の被験者と〜4000枚の画像であり、1人あたり平均14枚の画像でした。開発セットの対象の5〜10％を取り、残りはトレーニングに使用します。トレーニング中、システムは2番目のセットのサンプルのみを表示する必要があり、最初にそれをチェックします（ EERを考慮）。

データを共有するためのコードはこちらから入手できます。上記のアンパックされたデータセットへのパスを示すことのみが必要です。

ここで、データを前処理する必要があります。まず、顔をハイライトします。これは自分では行いませんが、dlibライブラリを使用します。

 import dlib import numpy as np from skimage import io image = io.imread(image_path) detector = dlib.get_frontal_face_detector() face_rects = list(detector(image, 1)) face_rect = face_rects[0]

ご覧のとおり、このライブラリを使用すると、数行のコードで顔を囲む四角形を取得できます。また、dlib検出器は、 OpenCVとは異なり、非常にうまく機能します。データベース全体からわずか12人の個人から、彼は検出できず、単一の誤検出を作成しませんでした。

私たちの仕事の正式な声明は、すべての人が同じサイズでなければならないことを意味します。この要件を満たし、同時にすべての顔を揃えて、キーポイント（目、鼻、唇）が常に画像上の同じ場所にくるようにします。選択したトレーニング方法に関係なく、このような手段が私たちを助け、確かに大きな害を与えないことは明らかです。アルゴリズムは簡単です：

単位正方形には、キーポイントの先験的な位置があります。
選択した画像サイズを知って、単純なスケーリングによって画像上のこれらのポイントの座標を計算します。
次の人のキーポイントを選択します。
2番目のポイントセットを最初のポイントセットにマッピングするアフィン変換を作成します。
アフィン変換を画像に適用して切り取ります。

dlibの例（face_template.npy、こちらからダウンロード）でキーポイントの参照位置を見つけます。

 face_template = np.load(face_template_path)

顔画像上のキーポイントを検索するには、例（shape_predictor_68_face_landmarks.dat、こちらからダウンロード）で見つけることができる既に訓練されたモデルを使用して、dlibを再度使用します。

 predictor = dlib.shape_predictor(dlib_predictor_path) points = predictor(image, face_rect) landmarks = np.array(list(map(lambda p: [px, py], points.parts())))

アフィン変換は、3つのポイントによって一意に定義されます。

 INNER_EYES_AND_BOTTOM_LIP = [39, 42, 57]

させる $（x_1 ^ 0、y_1 ^ 0）、（x_2 ^ 0、y_2 ^ 0）、（x_3 ^ 0、y_3 ^ 0）$ -私たちが翻訳したい出発点 $（x_1 ^ 1、y_1 ^ 1）、（x_2 ^ 1、y_2 ^ 1）、（x_3 ^ 1、y_3 ^ 1）$ 。次に、行列で表されるアフィン変換 $T$ 関係から見つけることができます

$\ begin {bmatrix} x_1 ^ 1＆amp; x_2 ^ 1＆amp; x_3 ^ 1 \\ y_1 ^ 1＆amp; y_2 ^ 1＆amp; y_3 ^ 1 \\ 1＆amp; 1＆amp; 1 \ end {bmatrix} = T \ begin {bmatrix} x_1 ^ 0＆amp; x_2 ^ 0＆amp; x_3 ^ 0 \\ y_1 ^ 0＆amp; y_2 ^ 0＆amp; y_3 ^ 0 \\ 1＆amp; 1＆amp; 1 \ end {bmatrix}。$

それを見つける：

 proper_landmarks = 227 * face_template[INNER_EYES_AND_BOTTOM_LIP] current_landmarks = landmarks[INNER_EYES_AND_BOTTOM_LIP] A = np.hstack([current_landmarks, np.ones((3, 1))]).astype(np.float64) B = np.hstack([proper_landmarks, np.ones((3, 1))]).astype(np.float64) T = np.linalg.solve(A, B).T

そして、scipy-imageライブラリを使用して画像に適用します。

 import skimage.transform as tr wrapped = tr.warp( image, tr.AffineTransform(T).inverse, output_shape=(227, 227), order=3, mode='constant', cval=0, clip=True, preserve_range=True ) wrapped /= 255.0

便利なAPIにラップされた完全な前処理コードは、 preprocessing.pyファイルにあります。

データ準備の最後のコードは正規化です。トレーニングベースに従って平均と標準偏差を計算し、それらの各画像を正規化します。開発セットについて忘れないでください。こちらのコードをご覧ください。

収集、分割、整列、および正規化されたデータは、ここからダウンロードできます。

ボーンアルティメイタム

データが見つかり準備されたので、テスト方法を整理しました。戦いの半分が終わった、残っている最も簡単なことは見つけることです $F$ 良いEERで問題を解決します。 EER = 10％がこのようなトレーニングタスクに非常に適しているとすぐに判断しましょう。実際、このようなシステムは、2つの写真で同一の顔を検索するなどの単純なアプリケーションでも使用できます。

コイン

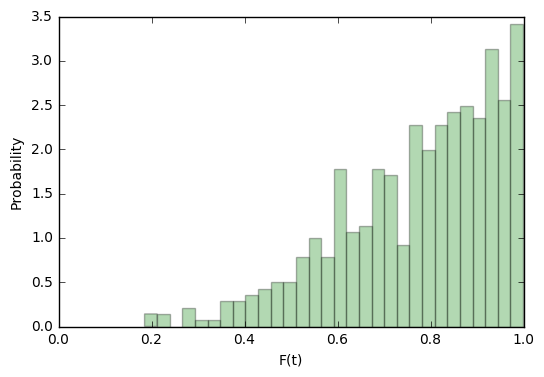
悪い機能のまさにその例から検索を始めましょう $F（x、y）= \ xi \ sim U [0; 1]$ 。開発セットからの写真のペアごとに、ランダムな値を取得し、それらにDET曲線を作成してEERを見つけます。

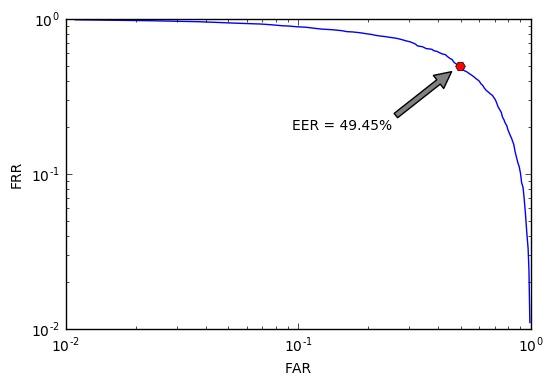
EER = 49.5％の場合、このような識別子は、各決定で投げるコインよりも優れていません。もちろん、これはグラフがなくても理解できますが、私たちの目標は、識別問題を解決する方法を学習し、明らかに悪い判断であっても、決定を客観的に評価できるようにすることです。さらに、プッシュするものがあります。

距離

からの2つのベクトルの機能は何ですか $R ^ {m \ times n}$ 実数を返すことが最初に思い浮かびますか？ほとんどの人がこの質問に答えると確信しています。距離です。確かに $R ^ {m \ times n}$ メトリック空間です。これは、任意の2つの要素を意味します $x$ そして $y$ 距離はそれから決定されます $Rのd（x、y）\$ さまざまな方法で入力できます。しかし、距離はゼロからプラスの無限まで変化するため、マイナスで考慮する必要があり、採用した形式化では、その逆も同様です。

たとえば、余弦距離を考えます。

$-d（x、y）= \ cos（x、y）= \ frac {x \ cdot y} {\ Vert x \ Vert \ cdot \ Vert y \ Vert}$

そして、開発セットで同じ操作をすべて行います。

 dev_x = np.load('data/dev_x.npy') protocol = np.load('data/dev_protocol.npy') dev_x = dev_x.mean(axis=3).reshape(dev_x.shape[0], -1) dev_x /= np.linalg.norm(dev_x, axis=1)[:, np.newaxis] scores = dev_x @ dev_x.T tsc, isc = scores[protocol], scores[np.logical_not(protocol)] eer, fars, frrs, dists = calc_metrics(tsc, isc)

このようなDET曲線が得られます。

EERは16％減少し、34.18％になりました。より良いが、まだ適用されない。もちろん、トレーニングセットと機械学習メソッドを使用せずに、関数のみを選択したためです。ただし、距離の概念は堅牢です。そのままにして、機能を紹介しましょう。 $F$ 形で

$F = d（f（x）、f（y））$

どこで $d$ -コサイン距離、および $f：R ^ {m \ times n} \ to R ^ k$ embedderと呼ぶ関数と、その作業の結果を宇宙から $R ^ k$ - 埋め込み 。彼女は、トレーニングセットから得られた事後の経験を考慮して、別の（必ずしも小さいとは限らない）次元のいくつかのスペースに画像を「埋め込み」ます。

CNN

さて、あなたと私はタスクをさらに単純化しました。良い機能を見つけるだけです $f$ 、システムの他のすべての部分はすでに配置されています。茂みに勝ちましょう-現時点では、CNN（Convolutional Neural Networks）よりも優れた画像を処理できるモデルは存在しないことがわかっています。次のように、それほど複雑ではないアーキテクチャの畳み込みネットワークを構築しましょう。

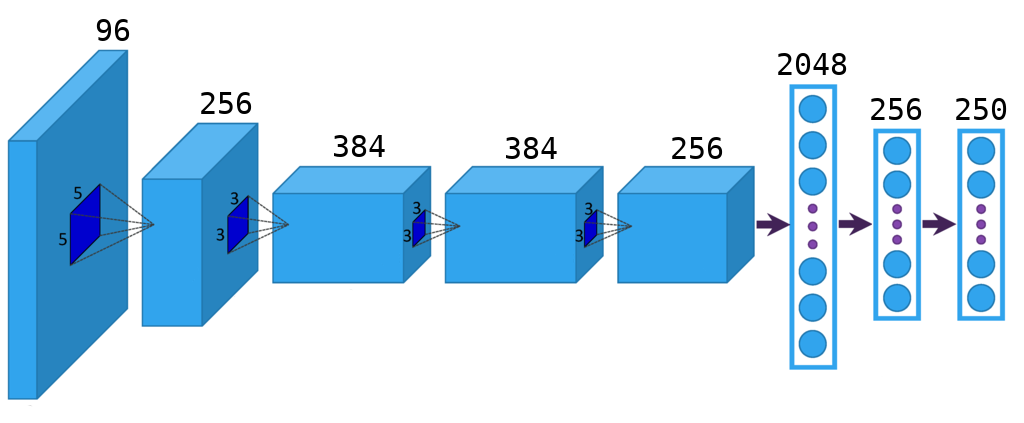
ケラスのモデル

 from keras.layers import Flatten, Dense, Dropout from keras.layers.convolutional import Convolution2D, MaxPooling2D from keras.layers.advanced_activations import PReLU from keras.models import Sequential model = Sequential() model.add(Convolution2D(96, 11, 11, subsample=(4, 4), input_shape=(dim, dim, 3), init='glorot_uniform', border_mode='same')) model.add(PReLU()) model.add(MaxPooling2D((3, 3), strides=(2, 2))) model.add(Convolution2D(256, 5, 5, subsample=(1, 1), init='glorot_uniform', border_mode='same')) model.add(PReLU()) model.add(MaxPooling2D((3, 3), strides=(2, 2))) model.add(Convolution2D(384, 3, 3, subsample=(1, 1), init='glorot_uniform', border_mode='same')) model.add(PReLU()) model.add(Convolution2D(384, 3, 3, subsample=(1, 1), init='glorot_uniform', border_mode='same')) model.add(PReLU()) model.add(Convolution2D(256, 3, 3, subsample=(1, 1), init='glorot_uniform', border_mode='same')) model.add(PReLU()) model.add(MaxPooling2D((3, 3), strides=(2, 2))) model.add(Flatten()) model.add(Dropout(0.5)) model.add(Dense(2048, init='glorot_uniform')) model.add(PReLU()) model.add(Dropout(0.5)) model.add(Dense(256, init='glorot_uniform')) model.add(PReLU()) model.add(Dense(n_classes, init='glorot_uniform', activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])

そして、トレーニングセットの古典的な分類の問題を解決することを彼女に教えます。250人の被験者のどれが顔写真を所有しているかを判断します。上記のコードに加えて、誰もがケラでこのような簡単なタスクを解決できます。また、5〜6行目も必要です。この記事で説明したトレーニングベースには、拡張を適用することが不可欠です。そうしないと、データが十分な結果を得ることができません。

あなたは、分類タスクがそれと何の関係があるのか、そしてその解決策はどのように私たちを助けるのでしょうか？正しくやる！以下で説明するアクションを理解するためには、非常に重要な仮定を立てる必要があります ：ネットワークが閉じた集合の分類問題をうまく解決することを学習した場合、次元256の最後から2番目のレイヤーに、対象がトレーニングセットに含まれていなくても、顔画像に関するすべての重要な情報が集中します。

訓練されたネットワークの最後の層から低次元の特徴を抽出するこの手法は広く普及しており、 ボトルネックと呼ばれています。ちなみに、kerasのボトルネックを処理するためのコードはこちらにあります。

ネットワークはトレーニングされ、256次元の属性が開発セットから抽出されました。 DET曲線を見てみましょう。

仮定は真実であることが判明し、 EERがさらに13％減少し、結果は21.6％に達しました。コインを投げるよりも2倍良い。それはさらに良いですか？もちろん、より大きくより多様なベースを構築し、より深いCNNを構築し、さまざまな正則化手法を適用できます...しかし、高品質の概念的アプローチを検討しています。そして、量はいつでも増やすことができます。袖にはまだもう1つの切り札がありますが、テーブルに置く前に少し気を散らさなければなりません。

ボーンエボリューション

結果を改善する鍵は、最適化の実現にあります $f$ トレーニングセットの情報だけでなく、機能に関する情報も使用できます。 $d$ 。確かに、修正しましょう $d$ そして私たちは訓練します $f$ 埋め込みを使用してスコアを取得する方法に関する先験的な知識に基づいています。 FaceNetの Googleの人々によって、このようなアプローチが初めて提案されました：顔認識とクラスタリングのための統合された埋め込み。

彼らが提案したアプローチはTDE （Triplet Distance Embedding）と呼ばれ、以下から構成されていました。 $f$ ソーススペースからのネットワークのような $R ^ {m \ times n}$ 埋め込みスペースへ $R ^ k$ 中間分類問題を解決する必要なく、修正します $d$ ユークリッド距離として、損失関数で考慮に入れます。どうやって？それは非常に直感的です。1つの被験者のベクトルを、ターゲット空間にできるだけ近づけ、他の被験者のベクトルから遠ざけるようにします。

トリプルを使用してこのようなネットワークを教えることが提案されました。 $（x_a、x_p、x_n）$ どこで $x_a$ （アンカー）および $x_p$ （ポジティブ）1つのエンティティに属し、かつ $x_n$ （負）別に。 3つのベクトルすべてについて、 埋め込みを構築します $f（x_a）$ 、 $f（x_p）$ そして $f（x_n）$ 。事前にパラメーターを尋ねます $\アルファ$ 。関係が次の場合、トリプルは良いと仮定します。

$\ Vert f（x_a）-f（x_n）\ Vert_2 ^ 2-\ Vert f（x_a）-f（x_p）\ Vert_2 ^ 2＆gt; \アルファ$

つまり、特定のアンカーについて、ポジティブとネガティブが存在するエリア間にギャップがあることを意味します $\アルファ$ 。この比率がトレーニングセットからのすべてのトリプルについて成り立つ場合、データを理想的に分割しました。そして、この不等式に違反しているトリプルでのみネットワークをトレーニングすることは理にかなっています。不等式に基づいて、ネットワークの損失関数を構築できます $f$ ：

$L（x_a、x_p、x_n、f）= \ frac {1} {N} \ sum_ {i = 1} ^ N \ Big [\ Vert f（x_a ^ i）-f（x_p ^ i）\ Vert_2 ^ 2 -\ Vert f（x_a ^ i）-f（x_n ^ i）\ Vert_2 ^ 2 + \ alpha \ Big]。$

このアプローチを使用して、著者はWildとYouTube Faces DB データセットのLabeled Facesのエラーを30％削減しました。これは間違いなく非常にクールです。ただし、このアプローチには問題があります。

多くのデータが必要です。
遅い学習
オプションパラメータ $\アルファ$ 選択方法は明確ではありません。
多くの場合（主に少量のデータで）、 softmax + bottleneckよりも動作が悪くなります。

ここに、シーンTPE （Triplet確率的埋め込み）があります。これは、顔検証とクラスタリングのためのトリプレット確率的埋め込みで説明されています。

追加のパラメーターを入力する理由 $\アルファ$ いつより単純な不平等を要求できるのでしょうか？ここにあります：

$d（f（x_a）、f（x_n））＆gt; d（f（x_a）、f（x_p））。$

それはオリジナルよりも簡単で解釈しやすいです。私たちに最も近い負の例は、私たちから最も遠い正の例よりも遠くにあることを望みますが、それらの間にギャップがあってはなりません。距離が離れてもネットワークの更新を停止しないという事実のため $\アルファ$ 埋め込みのグループは空間的に間隔を空けることができます $R ^ k$ さらに良い。

トリプレットが指定された不等式を満たす確率を計算できます。

$p = \ frac {e ^ {d（f（x_a）、f（x_p））}} {e ^ {d（f（x_a）、f（x_p））} + e ^ {d（f（x_a）、 f（x_n））}}。$

で割った $e ^ {d（f（x_a）、f（x_p））}$ ：

$p = \ frac {1} {1 + e ^ {d（f（x_a）、f（x_n））-d（f（x_a）、f（x_p））}} = \ sigma \ big（d（f（ x_a）、f（x_p））-d（f（x_a）、f（x_n））\ big）$

確率の対数を最大化するため、損失関数は次のようになります。

$L（x_a、x_p、x_n、f）=-\ frac {1} {N} \ sum_ {i = 1} ^ N \ log \ sigma \ big（d（f（x_a ^ i）、f（x_p ^ i ））-d（f（x_a ^ i）、f（x_n ^ i））\ big）。$

そして機能として $f$ 著者は、巨大なCNNではなく、単純なマトリックスの使用を提案しています。 $f（x）= Wx$ 既に受け取ったボトルネックの兆候について彼女に教えます。著者が達成した結果は次のとおりです。

ご覧のとおり、このアプローチは元のアプローチよりもうまく機能し、多くの利点があります。

必要なデータが少ない。
非常に速く学習します。
深すぎるアーキテクチャは必要ありません。
既存のトレーニング済みアーキテクチャの上で使用できます。

このアプローチを使用しています。このために必要なコードは20行だけです。

 def triplet_loss(y_true, y_pred): return -K.mean(K.log(K.sigmoid(y_pred))) def triplet_merge(inputs): a, p, n = inputs return K.sum(a * (p - n), axis=1) def triplet_merge_shape(input_shapes): return (input_shapes[0][0], 1) a = Input(shape=(n_in,)) p = Input(shape=(n_in,)) n = Input(shape=(n_in,)) base_model = Sequential() base_model.add(Dense(n_out, input_dim=n_in, bias=False, weights=[W_pca], activation='linear')) base_model.add(Lambda(lambda x: K.l2_normalize(x, axis=1))) a_emb = base_model(a) p_emb = base_model(p) n_emb = base_model(n) e = merge([a_emb, p_emb, n_emb], mode=triplet_merge, output_shape=triplet_merge_shape) model = Model(input=[a, p, n], output=e) predict = Model(input=a, output=a_emb) model.compile(loss=triplet_loss, optimizer='rmsprop')

プロジェクトでTPEを使用したい場合は、トリプレットを使用したトレーニングの最も重要な問題（その選択の問題）を取り上げなかったため、元の作品を読むのが面倒ではありません。小さなタスクでは、ランダム選択で十分ですが、これはルールというよりは例外です。

ボトルネックについてTPEをトレーニングし、今日の最後のDET曲線を見てみましょう。

12％ のEERは、私たちが望んでいたものに非常に近いものです。これは、CNNを使用するよりも2倍、ランダム選択よりも5倍優れています。もちろん、より深いアーキテクチャとより大きなベースを使用して結果を改善できますが、そのような結果は原則を理解するのに十分です。

考慮されているすべてのメソッドのDET-曲線の比較：

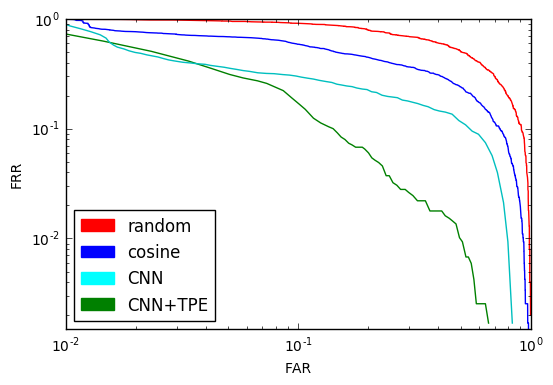
WebベースのインターフェースであろうとQtアプリケーションであろうと、あらゆる種類のエンジニアリングとシステムへのインターフェースを固定し、写真で同一の顔を検索するためのプログラムが用意されています。

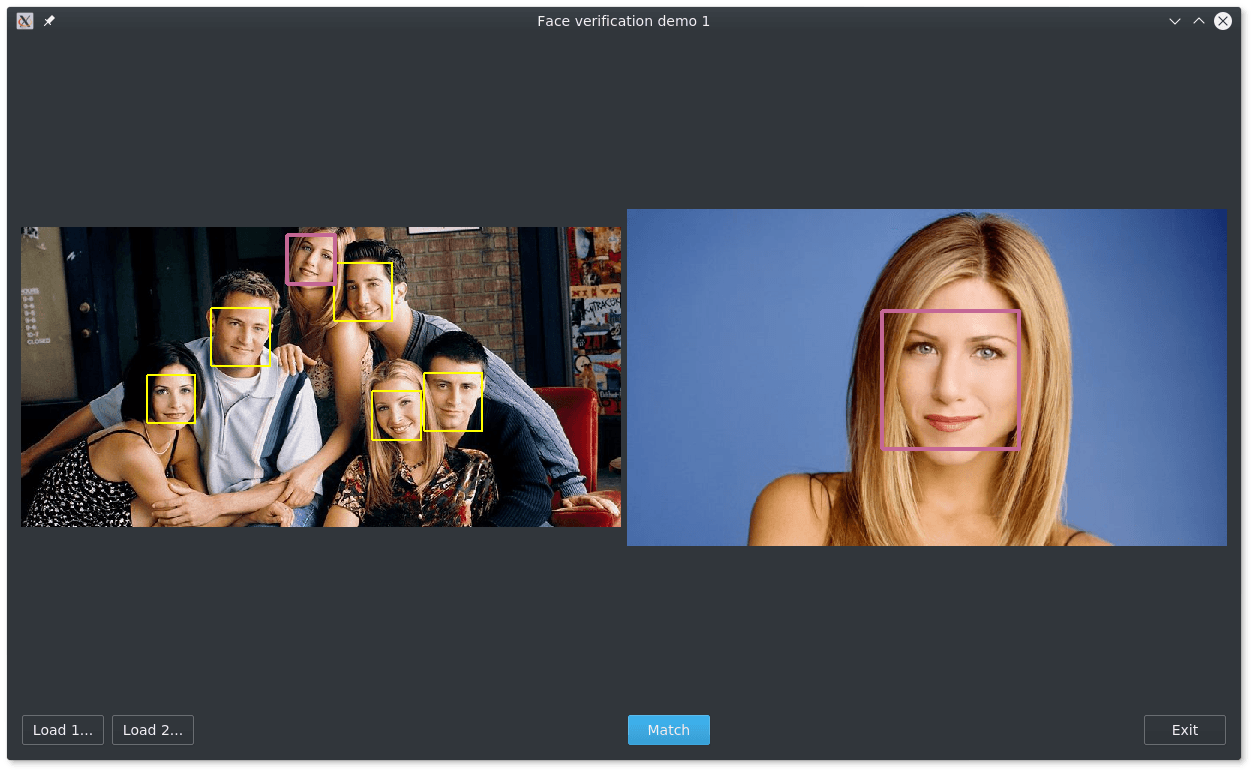
このアプリはGitHubで入手できます。

読んでくれてありがとう！同様に、プロフィールを購読し、コメントを残し、車を上手に教えてください。追加は大歓迎です。

なじみのある顔を探して

Bourneの識別（Bourneだけでなく）

ボーンスプレマシー

ベース準備

ボーンアルティメイタム

コイン

距離

CNN

ボーンエボリューション

文学

More articles: