過去10年間で、Rは長い道のりを歩んできました。ニッチな(通常はアカデミックな)楽器から、最も人気のあるプログラミング言語の主流の「ビッグ10」まで 。 この関心は、オープンソースのメンバーシップ、アクティブなコミュニティ、およびさまざまなビジネスタスクでの機械学習/データマイニング手法のアプリケーションの活発な成長セグメントなど、多くの理由によって引き起こされます。 お気に入りの言語の1つが自信を持って新しいポジションを獲得し、専門能力の開発から遠く離れた人でもRに興味を持ち始めるのを見るのは素晴らしいことですが、大きな問題が1つあります。 作成者によると、R言語は「統計学者のための統計学者」と書かれています。 したがって、何千もの追加パッケージは言うまでもなく、「すぐに使える」巨大で信頼性の高い機能を備えた、高レベルで柔軟性のあるものです。 同時に、根本的に異なるパラダイムを組み合わせて、非常に効率の悪いコードを書くための幅広い可能性を持っている、セマンティクスの面で非常に軽薄です。 そして、最近多くの人にとってこれが最初の「実際の」プログラミング言語であるという事実を考えると、状況はさらに脅威になります。
ただし、Rコードの実行の品質と速度の向上は、初心者だけでなく経験豊富なユーザーが常に直面する普遍的なタスクです。 そのため、非効率の原因とそれらを排除する方法を覚えるために、Rの最も単純な構造と基本原則に戻ることが非常に重要な場合があります。 この記事では、最初に財務戦略の研究に取り組んでいたときに、オンラインコースのトレーニングコースとして採用された1つのケースについて説明します。
マトリックスに行き詰まらない方法
関係のない詳細をすべて省略して、次のようにテスト問題を定式化できます。 任意の自然の サイズの行列をすばやく生成する必要がある
このように(例
1 2 3 4 5 2 3 4 5 4 3 4 5 4 3 4 5 4 3 2 5 4 3 2 1
これは、いわゆるハンケル行列の特殊なケースです。 ここでは、左上隅と右下隅には常に単一性が含まれ、側面の対角線全体(左下から右上隅まで)は数字で構成されます。
パラメータを期待するのは自然です 合理的な範囲、たとえば単位から数百まで変化する可能性があります。 したがって、別の関数として問題の解決策を省略し、
彼女の議論になります。
最も簡単な計算では、必要な行列は条件を使用して要素ごとに決定されることが示されています
build_naive <- function(n) { m <- matrix(0, n, n) for (i in 1:n) for (j in 1:n) m[i, j] <- min(i + j - 1, 2*n - i - j + 1) m }
必要なサイズのマトリックスを事前に初期化しても(最初の行が存在しない-メモリの事前割り当て-初心者による一般的な間違い )、この解決策は非常にゆっくりと動作します。 言語の専門家にとって、このような結果は非常に予測可能です。Rはインタープリター言語なので、サイクルの各反復には実行に多くのオーバーヘッドが伴います。 サイクルの最適でない使用の例は、おそらく、Rのすべての教科書にあります。そして、結論は常に同じです。可能であれば、いわゆるベクトル化された関数を使用してください。 これらは通常、低レベル(C)で実装され、非常に最適化されています。
したがって、この場合、行列要素が2つのインデックスの関数である場合 そして
outer
関数とpmin
関数の組み合わせがpmin
機能pmin
。
build_outer_pmin <- function(n) { outer(1:n, 1:n, function(i, j) pmin(i + j - 1, 2*n - i - j + 1)) }
pmin
関数は、入力と出力の両方でベクトルを操作するという点でmin
と異なります。 比較: min(3:0, 1:4)
共通の最小値(この場合はゼロmin(3:0, 1:4)
探し、 pmin(3:0, 1:4)
はペアワイズ最小値からのベクトルを返します: (1, 2, 1, 0)
1、2、1、0 (1, 2, 1, 0)
。 ベクトル化された関数の概念は、公式に定式化するのは簡単ではありませんが、一般的な考え方は明確です。 まさにそのような関数は、 outer
関数を引数として期待します。 素朴な解決策のように、 min
を渡すと機能しないのはこのためです。これを実行し、エラーが発生することを確認してください。 ところで、まだouter
とmin
組み合わせを使用したい場合、 Vectorize
関数でラップすることにより、 min
関数を強制的にVectorize
ます。
build_outer_min <- function(n) { outer(1:n, 1:n, Vectorize(function(i, j) min(i + j - 1, 2*n - i - j + 1))) }
この種の強制ベクトル化は、常に自然よりもゆっくりと動作することを覚えておく必要があります。 ただし、状況によっては、 Vectorize
を省くことができません-たとえば、マトリックス要素の定義に条件付きif
が含まれるif
です。
単純なソリューションの非効率性を取り除く別の方法-何らかの形でサイクルのネストを削除する-は、行列の単位元ではなく、ベクトルまたは部分行列を反復することになります。 多くのオプションがありますが、そのうちの1つだけを再帰的に示します。 マトリックスを中心から端まで「床ごとに」構築します。
build_recursive <- function(n) { if (n == 0) return(0) m <- matrix(0, n, n) m[-1, -n] <- build4(n - 1) + 1 m[1, ] <- 1:n m[, n] <- n:1 m }
この場合、高レベルの反復回数が (呼び出しスタックはループの役割を担います)。
最後に、基本関数Rのレベルでの最適化で目的の結果が得られない場合、常に別のオプションがあります。低速部分を可能な限り低いレベルで実装することです。 つまり、純粋なCまたはC ++でコードを記述し、コンパイルしてRから呼び出します。このアプローチは、その極端な効率性とシンプルさ、およびRcpp
パッケージがあるため、パッケージ開発者の間で人気があります。
library(Rcpp) cppFunction("NumericMatrix build_cpp(const int n) { NumericMatrix x(n, n); for (int i=0; i<n; i++) for (int j=0; j<n; j++) x(i, j) = std::min(i + j + 1, 2*n - i - j - 1); return x;}")
この方法でcppFunction
を呼び出すと、 build_cpp
関数が取得されます。これは、定義されている他の関数と同様に呼び出すことができます。 このアプローチの明らかな欠点のうち、コンパイルの必要性に注意することができます(これには時間がかかります) Rcpp
使用Rcpp
「特効薬」ではなく、C /
microbenchmark
パッケージ
意思決定の速度について話したとき、私たちは言語がどのように機能するかについての先験的な知識に依存していました。 理論は理論ですが、パフォーマンスの議論には実験を伴う必要があります-特定の例でランタイムを測定します。 さらに、そのような場合、測定値は絶対的な真実ではないため、すべてを自分でチェックして再確認することをお勧めします:これらはハードウェアとプロセッサの状態、オペレーティングシステムと測定時の負荷に依存します。
Rでのコード実行速度を測定するいくつかの典型的な方法があります。最も一般的なものの1つは、関数system.time
です。 この関数を使用するとき、彼らは通常system.time(replicate(expr, 100))
ます。 これは良い選択肢ですが、同じことをするパッケージがいくつかありますが、はるかに便利でカスタマイズ可能なデザインです。 実際、標準はmicrobenchmark
と呼ばれるパッケージであり、これを使用します。 すべての作業は、同じ名前の関数によって実行されます。この関数には、測定のために任意の数の式( 未評価の式を参照)を渡すことができます。 デフォルトでは、各式は100回実行され、実行時間に関する収集された統計が表示されます。
library(microbenchmark) measure <- function(n) { microbenchmark(build_naive(n), build_outer_min(n), build_outer_pmin(n), build_recursive(n), build_cpp(n)) } m <- measure(100) m Unit: microseconds expr min lq mean median uq max neval build_naive(n) 20603.310 21825.7975 24380.0332 22884.3255 24215.368 66753.031 100 build_outer_min(n) 22624.873 25430.4985 28164.4496 26662.8955 29028.744 84972.926 100 build_outer_pmin(n) 159.755 187.8325 295.3822 204.1985 225.069 3710.103 100 build_recursive(n) 1741.992 2822.2910 5990.9897 3241.1980 3918.055 55059.974 100 build_cpp(n) 21.321 23.4230 33.6600 34.2335 38.588 91.289 100
この結論では、測定結果は記述統計のセットを持つ表の形式で提示されます。 さらに、結果のオブジェクトを描画できます: plot(m)
またはggplot2::autoplot(m)
。
benchr
パッケージ
現在、式の実行時間を測定するために設計された別のパッケージ、 benchr
パッケージが開発されています。 機能と構文はmicrobenchmark
パッケージとほとんど同じですが、いくつかの重要な違いがあります。 簡単に言うと、これらの違いは次のように説明できます。
-
C ++ 11の タイマーに基づいた単一のクロスプラットフォーム測定メカニズムを使用します。 - ユーザーには、測定プロセスを構成するためのオプションがさらに提供されます。
- テキストおよびグラフィックの結果の出力は、より詳細で視覚的になります。
benhcr
パッケージはCRAN (3.3.2よりも古いバージョンRの場合)にあり、開発版はgitlabで入手できます 。そこにはインストール手順もあります。 この例でbenchr
を使用benchr
と、次のようになります(必要なのは、 microbenchmark
関数をbenchmark
関数に置き換えることだけです)。
install.packages("benchr") library(benchr) measure2 <- function(n) { benchmark(build_naive(n), build_outer_min(n), build_outer_pmin(n), build_recursive(n), build_cpp(n)) } m2 <- measure2(100) m2 Benchmark summary: Time units : microseconds expr n.eval min lw.qu median mean up.qu max total relative build(n) 100 21800 24300 25600.0 27400.0 28100.0 79300.0 2740000 906.00 build2(n) 100 24400 28800 30100.0 31600.0 33700.0 44000.0 3160000 1070.00 build3(n) 100 157 189 198.0 738.0 217.0 43400.0 73800 7.02 build4(n) 100 1820 1980 3380.0 4910.0 4050.0 50000.0 491000 120.00 build5(n) 100 21 27 28.2 29.4 30.5 50.1 2940 1.00
便利なテキスト出力(相対列を使用すると、最速のソリューションの利点をすばやく評価できます)に加えて、さまざまな視覚化を使用できます。 ところで、 ggplot2
パッケージがggplot2
ている場合、それはグラフの描画に使用されます。 何らかの理由でggplot2
を使用したくない場合は、 benchr
パッケージbenchr
を使用してこの動作を変更できbenchr
。 測定結果の3つの典型的な視覚化がサポートされるようになりました:ドットプロット、ボックスプロット、バイオリンプロット。
plot(m2) boxplot(m2) boxplot(m2, violin = TRUE)
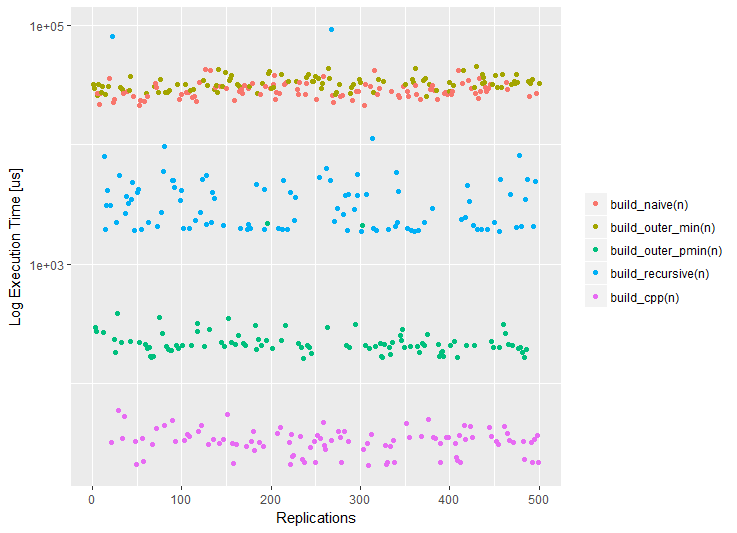


まとめ
したがって、測定結果に応じて、次の結論を定式化できます。
- 二重
for
ループが生成さfor
ため、参照(単純)ソリューションは低速ですR言語のベクトル化された方向に対応しない高レベルの反復。
- ベクトル化による強制ベクトル化を使用してループを
outer
関数に直接転送しても、問題は解決されません。これは、解決策が単純な解決策と意味的に同一であるためです。 - 再帰的な解決策は、高レベルの反復が
、 およびRの部分行列を使用した演算は十分に高速です。 -
pmin
関数の自然なベクトル化と組み合わせてouter
を使用すると、低レベルの実装(Cのコンパイル済み)により2桁高速になります。 -
Rcpp
パッケージRcpp
C ++言語の 最新機能を使用してさらに最適化されるため、Rcpp
への直接アクセスは3桁高速です(C ++のコンパイルにかかる時間を除く)。
そして、この記事で伝えたい最も重要なことです。 言語Rがどのように構成され、どの哲学が公言するかを知っている場合; 自然なベクトル化と基底Rの強力な関数セットを覚えている場合; 最後に、実行時間を測定する最新の手段を身に付ければ、最も困難なタスクでさえ非常に高揚することが判明し、コードの完成を待つのに長い分や時間を費やす必要はありません。
小さな免責事項: benchr
パッケージbenchr
、Artyom Klevtsov( @artemklevtsov )によって考案および実装され、私(Anton Antonov、 @ tonytonov )とPhilip マネージングディレクター ( @konhis )からの追加と改善がありました。 機能に関するバグの報告と提案を歓迎します。
このようなタスクは、Stepik.orgプラットフォームの「Rプログラミングの基礎」コースの基礎となりました。 コースは締め切りなしで開いており(自由なペースで受講できます)、 データ分析の専門的な再トレーニングプログラム (SPbAU RAS、 Institute of Bioinformatics )に含まれています 。
サンクトペテルブルクにお住まいの場合、SPb Rユーザーグループ( VK 、 meetup )の定期的な会議でお会いできてうれしいです。
トピックに関する資料と追加資料:
- Norman Matloff、The Art of R Programming:A Tour of Statistics Software Design
- パトリック・バーンズ、The R Inferno
- ハドリーウィッカムアドバンスドR
- Dirk Eddelbuettel、RcppとのシームレスなRおよび
C ++ 統合 - A. B.シプノフ、E。M.バルディンなど、視覚統計。 Rを使用します!