Clever Geek Handbook

JavaScriptカテゴリー理論。 パート1.セットのカテゴリ





抽象化は、ITの主要な手法の1つです。 プログラミング言語やモデリング言語、プログラミングパラダイム（手続き型、関数型、OOPなど）は、どのように、何から抽象化するかという質問に対する答えを提供します。 さらに、各アプローチの支持者は、ある種の抽象化を提供します。



真の普遍的な抽象化をご覧になりたい場合は、...に参加してください 。カテゴリの理論を研究してください 。 写真とJavaScriptコードを含むセットのカテゴリの例では、カテゴリ理論の最も基本的な概念である制限、ユニバーサルプロパティについて説明しています。 カテゴリ理論の計算面が考慮されます。



また、JavaScriptのクラス、不純物、およびブレンドについても少し説明します。



記事の例はこちらにあります 。



はじめに



誰もがカテゴリー理論について聞いたことがあると思います。 これはクールな銀の弾丸の理論であり、非常に異なるものを一様に記述することができると聞きました。 関数型プログラミング言語で積極的に使用されていると聞きました。 主にカテゴリー理論に基づいたプログラミング言語やコンピューター代数システムについて聞いたことがある人もいるかもしれません。



このトピックに関する多くの書籍や記事がインターネット上にあります。 しかし、通常は、数学者や科学や、Haskell、MLのような奇妙なことに従事するIT専門家に焦点を当てています（皮肉-カルマにマイナスを入れる必要はありません。通常、Saint Haskellに言及した後は無駄です）。



また、JavaScriptを使用して一切れのパンを毎日手に入れる単純な勤勉な労働者にとって、カテゴリー理論の利点はほとんど理解されていません。 この一連の記事を読んだ後、明確になるとは約束しません。 しかし、すべてがうまくいけば、多分便利なことをするアプリケーションを実行するでしょう。



私はすぐに、数学教育ではなく工学を持っていると警告します。 したがって、記事で厳密な定義、定理の証明などが見られると予想する場合、それは表示されません。 それどころか、すべては「指で」説明されます。 不正確な点があれば、書いてください、私はいくつかの点で間違っているかもしれません。



カテゴリとは何ですか？



カテゴリは、次のものに対して定義するものです。



記号∘は時々省略されます：（h g）f = h（g f）



また、合成の代わりに、射の連結が時々使用されるので、式ではそれらは図と同じ順序になります：（f; g）; h = f; （g; h）しかし、そのような記録は見た目ほど便利ではないため、まれです。 次の記事の要素を検討すると、これが表示されます。



何かのカテゴリを構築するには、それが必要です





形態素には、1つのソースと1つのターゲットオブジェクトが必要です。 3つ以上のオブジェクトを接続することも、「宙に浮かぶ」こともできません。 （ 高次のカテゴリは考慮しません。）



合成操作は、互換性のある射にのみ適用できます。 射：f→A→B、g：B→C、h：C→Dがあります。構成g∘f（またはf; g）は許容されます。 また、次の構成は許可されていません：h∘f、f∘f、f∘g。



次に、カテゴリの例を考えてみましょう。 基本的なトポを想像してください、それはカテゴリーです。 提示された場合、この記事で新しいものを見つけることはほとんどありません。 より基本的なものを読む方が良い。



グラフによって生成された無料のカテゴリの例



引き続き読み続ける場合は、より理解しやすいカテゴリを作成しようとします。 VKontakteページと、友達、購読者、購読している人のページを提示します。これらはすべて、直接接続しています。 これはオブジェクトのクラスになります ：









フォローしている全員に対して、ページからその人のページに矢印を描きます。 あなたをフォローしているすべての人に対して、自分のページからあなたのページに矢印を描きます。 そして、すべての友達のために、両方向に矢印を描きます：









次に、残りのページについても同じことを行います。









ある人が別の人をサブスクライブする場合、最初の人は2番目の人を知っていると想定します。 2人が互いにサブスクライブしている場合（友人）は、お互いを知っています。 つまり このカテゴリの射は、「知っている」という関係です。



誰もが自分自身を知っていて、 同一の射を描くと仮定します：









射の合成の操作を次のように定義します。



fをAがBを知っていることを示す射であり、gがBがCを知っていることを示す射であるとする。g∘fはAが間接的にCを知っていることを意味する射



したがって、このカテゴリの射のクラスには、「知っている」という関係だけでなく、「間接的に知っている」という関係も含まれます。



作曲の動作の関連性は明らかです。 AがBを知っており、Cを知っていて、Dを知っている場合、ここで射をグループ化しない方法は、とにかくAは間接的にDを知っています。



同一の射が合成の中立的な要素であることも明らかです。 AがBを知っている場合、自分自身を知っていても何も変わりません。



グラフによって生成される無料のカテゴリを作成しました 。 一方では、この例は、どのようにカテゴリからも構築する方法を示しています。 一方、特定のルールに従ってカテゴリが構築されることを示しています。



先行予約の例



前の例では、オブジェクトと射は比較的単純であり、内部構造が欠けていると考えています。



ここで、すべてのページ（あなたとあなたが接続している人々）が1つのオブジェクトであると想像してください。 他の人に関連する多くのページは異なるオブジェクトなどです。









このカテゴリにはどのような射がありますか？



たとえば、リレーション「サブセット」。 すべての友人、加入者など 個人Aも別の加入者などです。 人B、次にAからBへの射を描きます。この場合、カテゴリであるpreorderを取得します。









または、たとえば、射として、ページを引数として受け取り、それらのページを返す関数を使用できます。 この場合、セットのカテゴリを取得します。 セットのカテゴリには、VKontakteページのセットだけでなく、すべてのセットが含まれているため、より正確には、そのサブカテゴリです。



可換図



検討した例では、カテゴリを持つ図を特定しました。 しかし、一般的に、これらは2つの異なるものです。 厳密に言えば、 ダイアグラムはファンクターです。 これまでのところ、ファンクターとは何でも構いません。



以前の記事の 1つで、モデルとその表記法（図、テキスト表記、またはその他）が2つの異なるものであることを既に説明しました。 同様にカテゴリ。



ここでは、ダイアグラムは、オブジェクトがノードとして表され、射がノード間の矢印として表されるカテゴリフラグメントの一種の視覚的表現であると仮定します。 ただし、ダイアグラムでは、そのフラグメントだけでなく、カテゴリ全体を表すこともできます。 1つ以上のオブジェクトと射のみを含むカテゴリがあります。



チャートは、可換または非可換の場合があります。



可換図とは、任意のオブジェクトのペアについて、射の合成の結果がこれらのオブジェクト間の方向パスの選択に依存しない図です。



個人的には、ダイアグラムがどのように非可換になるかをすぐには理解しませんでした。 上記のグラフと事前予約によって生成された無料のカテゴリの例を見てください。 2つのオブジェクト間に複数のパスがある場合、これらすべてのパスは明らかに同等です。1つのオブジェクトで始まり、1つのオブジェクトで終わります。 これらのパスはどのように等しくないのでしょうか？



実際、予約注文では、最大で1つの射がオブジェクトAからオブジェクトBに移動できます。 無料のカテゴリでは、一対のオブジェクト間に複数の射が存在する可能性があります（コメントの説明を参照）が、この例ではこれらの射が同等であることは直観的に明らかです：これらは常にAが直接的または間接的にBを知っているという事実を反映しています。しかし、たとえば、オブジェクトの同じペア間のセットのカテゴリには、いくつかの完全に異なる射があります。 例として、2つのオブジェクトと2つの平行射を持つ非常に単純な図を考えてみましょう。 可換ですか？









等式f = gが成り立つ場合にのみ、可換です。 一般に、カテゴリー理論では、可換図は方程式系を書く代わりにしばしば使用されます。 「次の等式が成り立つ」と書いて、リストすることができます。 または、「次の図は可換である」と記述し、連立方程式に対応する図を描くことができます。



この図の可換性は、描画されたオブジェクトと射の背後にあるセットと関数に依存します。 オブジェクトAを数値のセット、オブジェクトBを幾何学的図形のセット、射影fはある数値に対してこの数値に等しい半径の円を返す関数、射影gは特定の数値に等しい辺の長さの正方形を返す関数としますこの番号に。 明らかに、これらの2つの関数は等しくありません。つまり、ダイアグラムは可換ではありません。









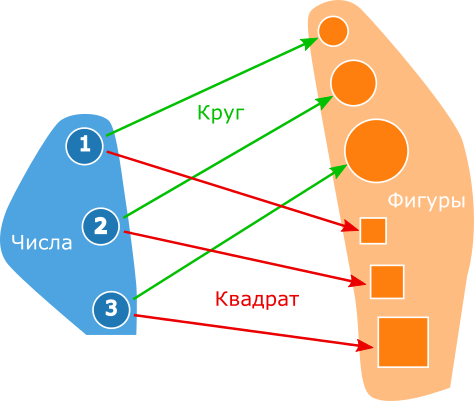
1つのカテゴリに数字のセットと数字のセットが混在していることを混同しないでください。 同じカテゴリには、多くのVKontakteページ、多くのセット、グラフ、シールなどがあります。これらはすべて、セットの1つのカテゴリです。 より詳細に検討しますが、最初にソースコードに関する少し一般的な情報を検討します。



ソースコードの一般情報



ソースコードはここにあり、記事の例はこちらにあります 。



私は、ES6がまだ設置されておらず、標準ライブラリに通常のコレクションがなかった3年前にほとんどのコードを書いたことをすぐに警告します。 その後、セットを実装する必要がありました。 そして、一般的に、コードはおそらく最適に編成されていません。 正直なところ、私はすべてをモジュールに分解して記事を読み、カテゴリ理論がこのすべての錫よりもはるかに簡単に見えることに気付きました。



Helpers.jsファイルでは、他のヘルパー関数とともに、拡張および結合関数が定義されています。 extend関数は長い間発明されてきました。これにより、あるクラスを別のクラスから継承することができます。詳細については、 ここで説明します 。 唯一のことは、私の実装ではクラスに不純物を追加できることです。 不純物についてのこの記事を読むことを強くお勧めします。 不純物はサブクラスの工場と見なされ、ES6でコンパクトに記述する方法について説明しています。 一般的に、スーパークラスが事前に知られていない、より一般的な継承のケースとしての不純物のビューは非常に興味深いです。



個人的には、Babelなどに煩わされたくないので、ソースコードはES5で書かれており、これら2つの機能が必要でした。 不純物は、extendを持つクラスとして継承することはできません。combinedメソッドを使用してのみ混合できます。



Category.jsファイルは、特定のカテゴリを継承する抽象クラス「category」を定義します。 また、不純物「完全カテゴリ」と「共重合カテゴリ」およびそれらの混合物「双極子カテゴリ」も定義します。 以下で検討するセットのカテゴリは、再び双極子カテゴリであり、任意の双極子カテゴリ「ミックス」で使用できる汎用アルゴリズムです。 JavaScriptは多重継承をサポートしないため、これらは特に不純物として実装されます。 さらに、これらすべてについて詳しく説明します。



Set.jsファイルは、1）セットのカテゴリ、2）セット自体、3）関数、および4）セットのカテゴリの制限を定義します。 理論的には、SetクラスはES6のSetに置き換えることができます。 関数は、いわゆるグラフの形式で実装されます 。 それらは明示的に保存します：





ドメインとコーディングドメインは明示的に保存されるため、2つの関数の構成が有効かどうかを確認できます。 1番目の関数のドメインが2番目の関数のコードネームと一致する場合にのみ有効です。 また、ドメインは、関数が本当に完全であるか、 部分的に定義された関数であるかを確認するために使用されます 。 コードを見ると、同様のチェック（アサート呼び出し）がたくさんあります。



関数をグラフではなく関数の形式で正確に格納することはおそらく可能ですが、これはまだ不可欠ではありません。



SetCategoryView.jsファイルで、d3に基づくセットのカテゴリのグラフ描画。 記事のほとんどすべての図は、その助けを借りて描かれています。 ところで、d3の4番目のバージョンでは、Force Layoutが改善され、そこで任意の力を個別に決定できるようになりました。 間違っていない場合は、svgのみで機能する前にドラッグアンドドロップを改善しました。現在、canvasで簡単にサポートされています。 この図では、理論的に興味深いものを見つけることができますが、完全なリファクタリングが必要です。



Set.htmlファイルには、この記事のすべての例が含まれています。



カテゴリの実装を設定する



次に、セットのカテゴリからのさまざまな構成と、それらがコードでどのように実装されるかを説明します。 それ自体は、次のファクトリとして実装されます。 



function SetCategory() { } extend(SetCategory, Category, BicompleteCategory); SetCategory.prototype.object = function (elements) { return new Set(elements); }; SetCategory.prototype.morphism = function (A, B, mapping) { return new TotalFunction(A, B, mapping); }; SetCategory.prototype.id = function (A) { return this.morphism(A, A).initId(); }; SetCategory.prototype.compose = function (g, f) { return g.compose(f); };


セットのカテゴリは抽象カテゴリから継承され、双極子カテゴリの動作はそれと混合されます。



このファクトリでは、作成することができます





正直なところ、カテゴリを工場にすべき理由をすぐには理解していませんでした。 言う、セット、リスト、スタック、ツリー、グラフ、およびその他の構造は通常、それらのすべての要素を明示的に保存します。 カテゴリは同様の数学的構造に似ていますが、なぜ実装が異なるのですか？ カテゴリをそのオブジェクトとモーフィズムのリポジトリとして実装することが不可能なのはなぜですか？ 一般的な場合、カテゴリには無限の数のオブジェクトと射が含まれているためです。 さらに、それらのうち、必要なものはわずかです。 そして、それらは、それらに基づいて新しいオブジェクトとモーフィズムを構築するために保存する必要はありません。



いくつかのオブジェクトと射を作成しましょう： 



 var setCat = new SetCategory(); var obj123 = setCat.object([1,2,3]); var objAB = setCat.object(['a','b']); var objABCD = setCat.object(['a','b','c','d']); var f = setCat.morphism(obj123, objABCD, {1: 'c', 2: 'c', 3: 'd'}); var g = setCat.morphism(objABCD, objAB, {'a': 'a', 'b': 'b'}); var h = setCat.morphism(objAB, obj123, {'a': 1, 'b': 1}); showSetCategoryView('diagram1', setCat, {'A': obj123, 'B': objABCD, 'C': objAB}, {'f': {dom: 'A', codom: 'B', morphism: f}, 'g': {dom: 'B', codom: 'C', morphism: g}, 'h': {dom: 'C', codom: 'A', morphism: h}});








実行可能なJavaScriptコードを記事に挿入できないのは残念です。 したがって、写真を挿入する必要がありますが、 ここですべてを移動できることを繰り返します 。



エピモルフィズム、単型、同型



さて、オブジェクト、モーフィズムを作成し、それらを美しく描くことができます。 次は？



オブジェクトと射はさまざまなプロパティを持つことができ、カテゴリ理論の重要な部分はこれらのプロパティの説明と研究に専念しています。 カテゴリ理論の実装では、これらのプロパティを検証でき、特定のプロパティを持つオブジェクトとモーフィズムを構築できる必要があります。 最も単純なプロパティから始めましょう。



セットのカテゴリ内の射は関数であるということを思い出させてください。 学校から、あなたはおそらく、機能が射影、注射、全単射であることを覚えています。 厳密な定義はなく、すべてを指で説明することを約束しました。



Surjectionは、値の範囲からすべての値を取得する関数です。 整数のセットで定義された2乗関数は、2、3、5、...の値をとらないため、射影ではありません。









インジェクションは、元のセットのさまざまな要素を結果セットのさまざまな要素にマッピングする関数です。 さらに、関数の値の範囲には、定義領域にプロトタイプを持たない追加の要素が含まれる場合があります。









全単射は1対1のマッピングです。 関数は、全射と射出の両方である場合にのみ、全単射です。









他の数学的オブジェクト（グラフなど）には、射影、射影、全射の類似物がいくつかあります。 したがって、カテゴリの理論では、この理論はすべてに関するものであるため、これらの概念を一般化することを決定し、それぞれエピモーフィズム、モノモーフィズム、およびアイソモーフィズムを導入しました。



この一般化とは何ですか？ カテゴリー理論では、オブジェクトと射の内部構造から完全に抽象化されているという事実。 上記の図で行われているように、これらのタイプの射を円と矢印で定義する代わりに、他の射との関係で定義されます。



エピモルフィズムは、e→A→Bであり、等式f∘e = g∘eはf = gを意味します（言い換えると、右側のeに短縮できます）。









危機にwhatしているものを明確にするために、NOTエピモーフィズムの例を示します。









上の図は可換です（f∘h = g∘h）。 これを確実にするために、セットAの各要素から矢印をたどることができ、選択されたパスに関係なく、常にセットCの同じ要素に到達します。 同じ引数に対する関数f∘hおよびg∘hは、同じ結果を返します。 しかし（！）関数fとgの等価性はこれからは続きません。 要素「1」の場合、異なる値「a」と「b」を返します。 しかし、関数hがエピモルフィズムである場合、fとgの等式は図の可換性から得られます。



さらに、「円を通る矢印による遷移」などの詳細は説明しませんが、セットのカテゴリで可換図について話しているときは、この可換性を常にこの方法でチェックできることに注意してください。



繰り返しますが、単射関数は他の関数との関係を通してのみ記述され、それらの内部構造の詳細から完全に抽象化されていることに注意してください。 これがカテゴリー理論の本質です。



単相性は、m = A→Bのようなm∘f = m∘gであるため、f = gに従う（つまり、左側のmで省略できる）射型です。









同型とは、逆が存在する型f：A→Bです。 射g：B→Aが存在し、f∘g = id Bおよびg∘f = id Aである









ここで、ちょっとした驚きがあります。 すべてのカテゴリではありませんが、射がエピモルフィズムであり、単相であるという事実は、同型であることを意味します。 これは、セットのカテゴリは確かにいくつかの概念を視覚化するのに適していますが、誤った類推につながる可能性があることを示しています。



終了、開始、およびヌルオブジェクト



最後のオブジェクトはオブジェクトTであり、任意のオブジェクトXに対して一意の射u：X→Tが存在します。



セットのカテゴリでは、最終オブジェクトはシングルトンであり、一意のモルフィズムは、元のセットの要素をシングルトンの単一要素にマッピングする関数です。 セットのカテゴリには無限の数の終端オブジェクトがありますが、それらはすべて互いに同型です。 これは、カテゴリ理論の観点からは、どのシングルトンが問題であるかは重要ではなく、同型に至るまでの1つに当てはまるすべてが他のシングルトンにも当てはまることを意味します。









初期オブジェクトはオブジェクトIであり、任意のオブジェクトXに対して一意の射u：I→Xがあります。



セットのカテゴリでは、初期オブジェクトは空のセットであり、空のセットで定義された一意のモルフザイムは空の関数です。 さらに、セットのカテゴリにはそれぞれ単一の空のセットがあり、単一の初期オブジェクトがあります。









nullオブジェクトは、開始オブジェクトと終了オブジェクトの両方であるオブジェクトです。



セットのカテゴリにゼロオブジェクトはありません。 セットを同時に空にしてシングルトンにすることはできません。



いくつかの重要な点に注意してください。



初期オブジェクトと最終オブジェクトは二重の概念であり、それらは射の方向の反転まで同等です。 最初のオブジェクトは、デュアルカテゴリの最後のオブジェクトになります（同じオブジェクトと合成操作を持つカテゴリですが、射は反対方向に向けられます）。 双対性または双対性の概念は、カテゴリー理論において非常に重要です。 以下に、デュアルコンセプトの例をいくつか示します。



ちなみに、有限オブジェクトはconach、初期オブジェクト-konechnyと呼ばれますが、ここでは、1つの根本的に新しいプログラミング言語の分野にすでに分類されています。 概念に接頭辞「co-」を追加または削除すると、二重の概念が得られます。 カテゴリ理論の専門家は、初期のオブジェクトについて話していることを理解する必要がありますが、私はkokonechnyeオブジェクトに会いませんでした。



上記の定義は、最終オブジェクトから導かれた射については何も言っていません。 そしてそれらは存在します。 たとえば、モルフィズムf：{1}→{1,2,3,4}とグラフ{（1,1）}、またはモルフィズムgと同じシグネチャでグラフ{（1,2）}。 つまり それらは存在するだけでなく、ユニークでもないため、将来を見据えてかなり重要な役割を果たします。 したがって、射がそれらにのみ向けられているオブジェクトとしての有限オブジェクトの概念は真実ではありません。









最初のオブジェクトに向けられた射については、何も言えません。 セットのカテゴリでは、それらは存在しないか、空の一意の関数であると想定しています。 原則として、なぜ1つではありません。 しかし、その後、各セットは空のセットと同型になります。 誰かがこの点を明確にできれば、それは素晴らしいことです。



ユニバーサルプロパティと最も重要なポイント



上記の定義の「...射は1つだけです...」というフレーズに注意してください。 これは一般的にカテゴリー理論の研究で見られます。 これは「 ユニバーサルプロパティ 」と呼ばれます 。



ユニバーサルプロパティを使用すると、詳細から抽象化して概念を定義できます。 開始オブジェクトと終了オブジェクトは、空のセット、シングルトン、はい、および一般的にはすべての構造に言及せずに定義されていることがわかります。 さて、これは本当の抽象化です！ 開発者向けのカテゴリー理論のガイドでは、 デカルトの閉じたカテゴリーやモナドではなく、主にそのようなことについて話す必要があると思います。



言い換えれば、カテゴリー理論では、オブジェクトを内部実装の説明ではなく、外部動作の説明、他のオブジェクトとどのように「相互作用する」ことができるか、に焦点を当ててオブジェクトを定義します。 確かに、プログラミング言語で通常行われていることとは少し異なりますが、このカテゴリの理論は興味深いものです。



詳細からの抽象化により、ユニバーサルプロパティは同型までのオブジェクトを定義します。 セットのカテゴリでは、すべての有限オブジェクト（シングルトン）が同型であることを既に述べました。 しかし、これは、ユニバーサルプロパティを介して定義されたオブジェクトには当てはまります。 原則として、これは非常に論理的です。2つのオブジェクトが外部で同じように「振る舞う」場合（それらは同じ普遍的な特性を持っています）、それらは同型です。



そして、おそらく、この一連の記事全体の最も重要なポイントです。 通常、ユニバーサルプロパティには最適化タスクがあります。これは、ある意味で最適なオブジェクトまたは射を見つけることです。 イコライザーのセクションでこれに戻ります。



最終オブジェクトと初期オブジェクトの実装



理論が多すぎるので、有限オブジェクトと初期オブジェクトがどのようにコードに実装されているかを見てみましょう。 
 SetCategory.prototype.terminal = function () { return new SetTerminalObject(this).calculate(); }; function SetTerminalObject(cat) { this.cat = function () { return cat; }; } SetTerminalObject.prototype.calculate = function () { this.obj = new Set([1]); return this; } SetTerminalObject.prototype.univ = function (A) { var mapping = {}; A.forEach(function (el) { mapping[el] = 1; }); return this.cat().morphism(A, this.obj, mapping); } SetCategory.prototype.initial = function () { return new SetInitialObject(this).calculate(); }; function SetInitialObject(cat) { this.cat = function () { return cat; }; } SetInitialObject.prototype.calculate = function () { this.obj = new Set(); return this; } SetInitialObject.prototype.univ = function (A) { return this.cat().morphism(this.obj, A, {}); }


あなたは質問をしたかもしれません：なぜシングルトンとEMPTYセットを実装するのにそんなに多くのコードがあるのですか？



最終オブジェクトと初期オブジェクトは、単なるセットではありません。 普遍的な特性は、それらのためにまだ満たされなければなりません。それは、いくらかの理論的特性を持ちませんが、計算で積極的に使用されます。 たとえば、コードカートの正方形の補数を計算する場合、オブジェクトの合計の普遍射が計算されます。 これについては後で説明します。



実装では、ユニバーサルプロパティを持つ構造体にメソッドがあります。





仕事



指の厳密でない定義を継続し、少し複雑なオブジェクトを検討します。



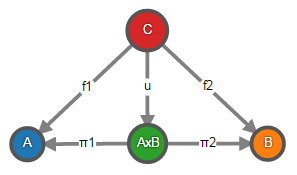
オブジェクトX jの積はオブジェクトXと射影πj：正準射影と呼ばれるX→X jであり、任意のオブジェクトYと射影f j ：Y→X jに対して一意の射影u：Y→Xが存在し、πj ∘u = f j 。



カテゴリ理論では、πj∘u = f jの形式の等式を書く代わりに、同様の図を描き、それが可換であると言うことができます（2つのオブジェクトの例ですが、一般的な場合はもっとあります）：









セットのカテゴリでは、オブジェクトの積はセットのデカルト積です。









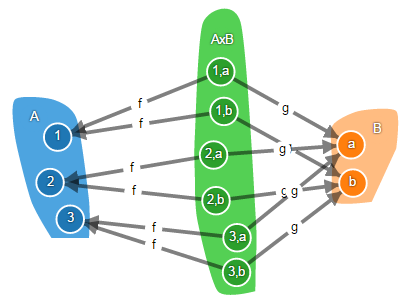
図では、製品はAxBとして示され、その要素は元のセットの要素のペアとして示されています。 しかし、これは明確にするために行われ、絶対に必要ではありません！ 作品は何でも呼ぶことができますが、その要素は





積は、値のペアのセットとしてではなく、射の関係を通じて定義されます。 集合のデカルト積とカテゴリー理論のオブジェクトの積の定義を比較します—共通点はありません。 カテゴリ理論の詳細から抽象化する例が再び表示されます。



コードでは、作業は次のように実装されます。 
 SetCategory.prototype.product = function (A, B) { return new SetProduct(this).calculate(A, B); }; function SetProduct(cat) { this.cat = function () { return cat; }; } SetProduct.prototype.calculate = function (A, B) { var obj = new Set(); var mapping1 = {}; var mapping2 = {}; A.forEach(function (x) { B.forEach(function (y) { var z = [x, y].toString(); obj.add(z); mapping1[z] = x; mapping2[z] = y; }); }); this.obj = obj; this.f = this.cat().morphism(this.obj, A, mapping1); this.g = this.cat().morphism(this.obj, B, mapping2); return this; }; SetProduct.prototype.univ = function(m, n) { assertEqualDom(m, n); assertEqualCodom(this.f, m); assertEqualCodom(this.g, n); var obj = m.dom(); var mapping = {}; obj.forEach(function (x) { var s1 = this.f.preimage(m.image(x)); var s2 = this.g.preimage(n.image(x)); mapping[x] = s1.intersection(s2).representative(); }.bind(this)); var u = this.cat().morphism(obj, this.obj, mapping); assertCommutes(this.f.compose(u), m); assertCommutes(this.g.compose(u), n); return u; };


計算関数は、集合のデカルト積だけでなく、2つの射（元のオブジェクト上の積の正準投影）も計算することに注意してください。 ほとんどの計算では、主な役割を果たすのは彼らであり、大まかに言えば、彼らは多くの人よりもはるかに重要です。



univ関数は、一部のオブジェクトと一対の射について、普遍射（上図のu-）を計算します。 作品の普遍的な形態がどのように役立つかを見てみましょう。



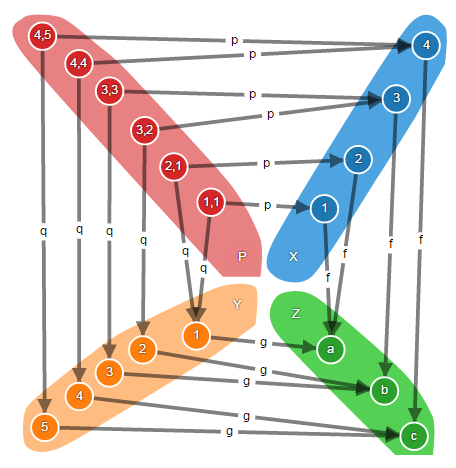
次の図では、オブジェクトAとB、それらの積AxB、およびモルフィズムf 1とf 2を持つ任意のオブジェクトCが表示されています。









セットCの要素「1」がセットAの要素「1」とセットBの要素「a」にマッピングされていることがわかります。セットAxBの要素「1」と同様です。 普遍射の計算では、この事実を確立し、集合Cの要素「1」を集合AxBの要素「1、a」にマッピングするように、普遍射を構築します。



集合Cの要素「4」と「5」は、射f 1とf 2によって同じ要素にマッピングされます。 したがって、普遍射は、それらを集合AxBの「2、b」の1つの要素にマッピングします。



明確にするために、Cがたくさんの猿だと想像してください。 f 1各猿は、美しいまたはbeautifulいカテゴリのいずれかに属し、f 2-スマートまたは愚かなカテゴリのいずれかに属します。 次に、普遍的な射影uは、各猿を4つのカテゴリのいずれかに割り当てます：美しいとスマート、美しいと愚か、stいとスマート、と愚か。



実際、製品の普遍射は射の生成物です。



さまざまな形式の作業は、さまざまなプログラミング言語で実装されています。 これらは、構造、タプル、およびSQL、LINQなどのあらゆる種類の結合です。 types-worksについて読んでください。



JavaScriptでは、作品の標準的な投影はデストラクタまたはアクセサと見なすことができます。 



 monkeyKind.a monkeyKind.b


コンストラクターとしての普遍射： 



 function u(x) { return { a : isBeautiful(x), b : isSmart(x) }; }


カテゴリ理論では、アクセッサはデストラクタと呼ばれることがよくあります。これは、複雑なオブジェクトを構成要素に解析できるため、デザイナと重複しています。 そのようなデストラクタを呼び出す場合、オブジェクトをまったく破棄する必要はありません。



金額



オブジェクトX jの合計は、オブジェクトXと射影i j ：X j →Xであり、正準埋め込みと呼ばれ、任意のオブジェクトYと射影f j ：X j →Yに対して、u X X i j = f j 。



2つのオブジェクトの可換図の例：









セットのカテゴリでは、オブジェクトの合計はセットの選言的結合です。 つまり 結合されたセットに一致するオブジェクトがある場合、これらのオブジェクトはマージされませんが、大まかに言えば、各オブジェクトがどのセットからのものであるかを理解できるように、何らかの方法でマークされます。









集合論では、選言的和集合の要素は通常、たとえば1 A 、2 A 、3 A 、a B 、b Bなど、いくつかのタグまたはインデックスでマークされます。 しかし、この例では、合計の要素は1〜5の単純な数字であり、射影fとgによって元のセットの要素に関連付けられています。 そして、和の要素を「ラベル付け」するのはまさにこれらの射である。 作品に関しては、射のない集合自体は特別な役割を果たしません。



明らかに、積と合計は二重の概念です。 それらは、射の反転まで同様に定式化されます。



しかし、一般化はそこで終わりません。 製品と量は、それぞれ最終オブジェクトと初期オブジェクトに非常に似ています。 作品および有限オブジェクトの場合、特定の条件を満たすカテゴリの各オブジェクトから普遍型を作成することができます-このような構成は制限と呼ばれます 。 和オブジェクトと初期オブジェクトの場合、特定の条件を満たすカテゴリの各オブジェクトに対して普遍射を構築することができます-そのような構造はcolimitsと呼ばれます 。 さらに、制限と共同制限の例がさらに表示されます。



一般的な場合、（co）制限は、ある図に対して定義された（co）コーンです。 私が言ったように、チャートは、あるインデックスカテゴリから現在のカテゴリへのファンクターです。 おおまかな場合は、インデックスカテゴリによってダイアグラムの「フォーム」、「外観」が決定され、最終的に取得する（共同）制限（最終オブジェクト、製品など）が決定されます。 このアイデアをさらに発展させると、カコドモンを引き起こすリスクが生じます。







要するに、アイデアは、上記で検討したような一般的な概念でさえ、さらに強力に一般化できるということです。



, , , () «» . .



(). 
 SetCategory.prototype.coproduct = function (A, B) { return new SetCoproduct(this).calculate(A, B); }; function SetCoproduct(cat) { this.cat = function () { return cat; }; } SetCoproduct.prototype.calculate = function (A, B) { this.obj = new Set(); var elementCount = 1; function createInjection(set, obj) { var mapping = {}; set.forEach(function (x) { obj.add(elementCount); mapping[x] = elementCount; elementCount++; }); return mapping; } this.f = this.cat().morphism(A, this.obj, createInjection(A, this.obj)); this.g = this.cat().morphism(B, this.obj, createInjection(B, this.obj)); return this; }; SetCoproduct.prototype.univ = function(m, n) { assertEqualCodom(m, n); assertEqualDom(this.f, m); assertEqualDom(this.g, n); var obj = m.codom(); var mapping = {}; function addMappings(f, h) { h.dom().forEach(function (x) { mapping[f.image(x)] = h.image(x); }); } addMappings(this.f, m); addMappings(this.g, n); var u = this.cat().morphism(this.obj, obj, mapping); assertCommutes(u.compose(this.f), m); assertCommutes(u.compose(this.g), n); return u; };


, .









, , – . – .



, , – . - . . , . JavaScript , .



– – : 



 function Chimpanzee() { } function Gorilla() { }


p, – q, – C. , C – : , , . p , , q : 



 function u(x) { if (x instanceof Chimpanzee) { return p(x); } else if (x instanceof Gorilla) { return q(x); } }


( )



- , - . , , ? , , coproduct complement. . , , .



A+B, A i 1 . i 1 , A, – A+B. i 2 , :









. 
 SetCategory.prototype.coproductComplement = function (f) { return new SetCoproduct(this).complement(f); }; SetCoproduct.prototype.complement = function (f) { this.obj = f.codom(); this.f = f; this.g = this.cat().morphism(f.codom().diff(f.image()), this.obj).initId(); return this; };


N-, . . .





() ( ) ( ). () , .. .



f, g : X → Y – E eq : E → X, f ∘ eq = g ∘ eq O m : O → X f ∘ m = g ∘ m, u : O → E, eq ∘ u = m, .. .









… . - . . -, , , . , , . , . -, , . - . .



f ∘ eq = g ∘ eq. X eq , f g .









f g «1» X «a» Y. , eq «1» E «1» X, f(eq(1)) = g(eq(1)) = a. , , «1» E, Y.



f «2» «a», g «2» «b». , eq, «2» X . つまり f(eq(?)) = a g(eq(?)) = b, «a» «b».



X Y E eq. «1» «3» f g .



, E eq - f g. O m u? , E eq, , . O m, f ∘ m = g ∘ m.









, m f g , eq. eq m? . , E eq , O m , , . , , , , . - , , .



, ? . E O h, m ∘ h = eq, {(1,1),(3,3)} {(1,2),(3,3)}. , , O m , .



, , E eq - . O m u = {(1,1),(2,1),(3,3)}. O m, f ∘ m = g ∘ m, , .



O m E eq? ? , .



, , JavaScript! , , , ().



(), . 
 SetCategory.prototype.equalizer = function (f, g) { return new SetEqualizer(this).calculate(f, g); }; function SetEqualizer(cat) { this.cat = function () { return cat; }; } SetEqualizer.prototype.calculate = function (f, g) { assertParallel(f, g); this.f = function () { return f }; this.g = function () { return g }; var dom = new Set(); var codom = f.dom(); this.q = this.cat().morphism(dom, codom); f.dom().forEach(function (x) { if (f.image(x) == g.image(x)) { dom.add(x); this.q.push(x, x); } }.bind(this)); this.obj = this.q.dom(); assertCommutes(f.compose(this.q), g.compose(this.q)); return this; } SetEqualizer.prototype.univ = function (m) { assertEqualCodom(this.q, m); assertCommutes(this.f().compose(m), this.g().compose(m)); var mapping = {}; m.forEach(function (x, y) { mapping[x] = this.q.preimage(y).representative(); }.bind(this)); var u = this.cat().morphism(m.dom(), this.obj, mapping); assertCommutes(this.q.compose(u), m); return u; };


. , – . , f ∘ eq = g ∘ eq f ∘ m = g ∘ m … . , , ? .



f = g. , , , f g. , , , . , . f g , eq ( ).



, ? . O E . , , – ( ), , .



? , «» , (, ) . , , .





f, g : X → Y – Q q : Y → Q, q ∘ f = q ∘ g O m : Y → O m ∘ f = m ∘ g, u : Q → O, u ∘ q = m, .. .









, , . , , , , .



.









f g, , «1» X «a» Y. q(f(1)) = q(g(1)), , q «a» «a» Q.



f «2» «b», g «2» «c». q(f(2)) = q(g(2)), q «b» «c» «b» Q. , «b» «c» «b».



f «3» «c», g «3» «d». , , «c» «d» . «c» «b», , «d» «b».



«e» «e» «f». Q q.



, , O m, m ∘ f = m ∘ g. , O m , Q q.









O m , , , Q q. , , «a» «b», «1».



, . – . , () .



, . 
 SetCategory.prototype.coequalizer = function (f, g) { return new SetCoequalizer(this).calculate(f, g); }; function SetCoequalizer(cat) { this.cat = function () { return cat; }; } SetCoequalizer.prototype.calculate = function (f, g) { assertParallel(f, g); this.f = function () { return f }; this.g = function () { return g }; var dom = f.codom(); var codom = new Set(); var eq = {}; f.dom().forEach(function (x) { var fx = f.image(x); var gx = g.image(x); eq[fx] = eq[gx] = has(eq, fx) ? eq[fx] : has(eq, gx) ? eq[gx] : fx; }); this.q = this.cat().morphism(dom, codom); dom.forEach(function (s) { var t = eq[s] || s; codom.add(t); this.q.push(s, t); }.bind(this)); this.obj = this.q.codom(); assertCommutes(this.q.compose(f), this.q.compose(g)); return this; } SetCoequalizer.prototype.univ = function (m) { assertEqualDom(this.q, m); assertCommutes(m.compose(this.f()), m.compose(this.g())); var mapping = {}; m.dom().forEach(function (x) { mapping[this.q.image(x)] = m.image(x); }.bind(this)); var u = this.cat().morphism(this.q.codom(), m.codom(), mapping); assertCommutes(u.compose(this.q), m); return u; };


– . : , , . . .



( )



. , , ? – .



f : X → Z g : Y → Z – P p : P → X q : P → Y, f ∘ p = g ∘ q Q m : Q → X n : Q → Y, f ∘ m = g ∘ n, u : Q → P, p ∘ u = m q ∘ u = n, .. .









, - :









, P X Y, , , , f g Z.



, , , .



. 
 CompleteCategory.prototype.pullback = function (f, g) { return new Pullback(this).calculate(f, g); }; function Pullback(cat) { this.cat = function () { return cat; }; } Pullback.prototype.calculate = function (f, g) { assertEqualCodom(f, g); this.f = f; this.g = g; var prod = this.cat().product(f.dom(), g.dom()); this.product = function () { return prod; }; var eq = this.cat().equalizer(f.compose(prod.f), g.compose(prod.g)); this.equalizer = function () { return eq; }; this.p = prod.f.compose(eq.q); this.q = prod.g.compose(eq.q); this.obj = eq.obj; assertCommutes(this.f.compose(this.p), this.g.compose(this.q)); return this; } Pullback.prototype.univ = function (m, n) { assertEqualDom(m, n); assertEqualCodom(m, this.p); assertEqualCodom(n, this.q); var u = this.equalizer().univ(this.product().univ(m, n)); assertCommutes(this.p.compose(u), m); assertCommutes(this.q.compose(u), n); return u; };


. X Y, f ∘ π 1 g ∘ π 2 . – P . p π 1 ∘ eq, q – π 2 ∘ eq. .









, : , , .. , , , . , . , , .



( )



f : Z → X g : Z → Y – P p : X → P q : Y → P, p ∘ f = q ∘ g Q m : X → Q n : Y → Q, m ∘ f = n ∘ g, u : P → Q, u ∘ p = m u ∘ q = n, .. .









i 1 ∘ f i 2 ∘ g, i 1 i 2 – X Y. p q h ∘ i 1 h ∘ i 2 , h – :









, P – X Y, , Z, :









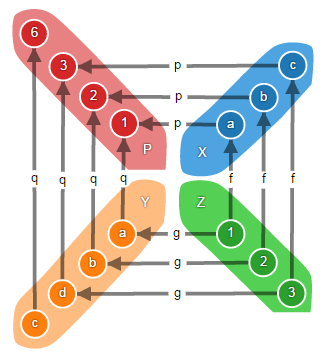
. , «a» «b» X Y P «1» «2» . «c» X «d» Y. «c» Y .



. g q. f p, X P , Y. . .



, (, , ) , :



. 
 CocompleteCategory.prototype.pushout = function (f, g) { return new Pushout(this).calculate(f, g); }; function Pushout(cat, f, g) { this.cat = function () { return cat; }; } Pushout.prototype.calculate = function (f, g) { assertEqualDom(f, g); this.f = f; this.g = g; var cp = this.cat().coproduct(f.codom(), g.codom()); this.coproduct = function () { return cp; }; var ceq = this.cat().coequalizer(cp.f.compose(f), cp.g.compose(g)); this.coequalizer = function () { return ceq; }; this.p = ceq.q.compose(cp.f); this.q = ceq.q.compose(cp.g); this.obj = ceq.obj; assertCommutes(this.p.compose(this.f), this.q.compose(this.g)); return this; } Pushout.prototype.univ = function (m, n) { assertEqualCodom(m, n); assertEqualDom(m, this.p); assertEqualDom(n, this.q); var u = this.coequalizer().univ(this.coproduct().univ(m, n)); assertCommutes(u.compose(this.p), m); assertCommutes(u.compose(this.q), n); return u; };




, , , JavaScript ML:

» DE Rydeheard, RM Burstall. Computational Category Theory, 1988



, :

» Hans Jürgen Schneider. Graph Transformations. An Introduction to the Categorical Approach, 2011



, , , , , :

» Peter Smith, Category Theory. A Gentle Introduction, 2016



, :

» Maarten M. Fokkinga. A Gentle Introduction to Category Theory — the calculational approach, 1994



, :

» Andrea Asperti, Giuseppe Longo. Categories, Types and Structures. Category Theory for the working computer scientist, 1991

» Michael Barr, Charles Wells. Category Theory for Computing Science, 1998



, « » ( — Bartosz Milewski ), , , , . , .



. , , . , . — . , , . , , , 1- :

» Michael Barr, Charles Wells. Toposes, Triples and Theories, 1985



, , David I. Spivak . , .



:

» Michael J. Healy. Category Theory Applied to Neural Modeling and Graphical Representations, 2000



おわりに



. , , , . , .



, . . , Haskell Hask. . , , . . . - .



. , , , . . , , , .



, – , , .



.



-, , . , calcCartesianProduct(), - multiplyFunctions(). , , — . つまり .



-, , , .



-, , . , ( assert ). , - , !



, , . , , , , . , . «», .



, - JavaScript.



. , .



» .


More articles:


All Articles