KDツリーの構造

この記事はKDツリーに完全に専念しています。KDツリーの構築の複雑さ、KDツリーでの「隣接」検索機能の実装の微妙さ、およびアルゴリズムの特定のサブタスクを解決するプロセスで発生する可能性のある「落とし穴」について説明します。 読者を専門用語（飛行機、超飛行機など）と混同しないようにするため、そして実際に便宜上、主なアクションは3次元空間で行われると想定されています。 ただし、必要に応じて、異なる次元の空間で作業することに注意してください。 私の意見では、この記事はプログラマーとアルゴリズムの学習に興味があるすべての人にとって有用です。誰かが自分自身のために新しい何かを見つけ、誰かが単に資料を繰り返し、コメントの記事を補足するかもしれません。 いずれにせよ、私は猫の下のすべての人に尋ねます。

はじめに

KDツリー （K次元ツリー）、特別な「幾何学的な」データ構造で、この空間を超平面（ K> 3 ）、平面（ K = 3 ）、直線で区切ることにより、K次元空間を「より小さい部分」に分割できます（ K = 2 ）よく、1次元空間の場合、ポイント（そのようなツリーで検索することにより、 バイナリ検索に似たものが得られます ）。

このようなパーティションは通常、K次元空間の検索範囲を狭めるために使用されるのが論理的です。 たとえば、ポイントに近いオブジェクト（頂点、球、三角形など）の検索、ポイントの3Dグリッドへの投影、レイトレーシング（レイトレーシングでアクティブに使用）など。 同時に、空間オブジェクトは特別な平行六面体- バウンディングボックスに配置されます（バウンディングボックスのみを作成する場合、オブジェクトの元のセットまたはオブジェクト自体を記述する平行六面体のようなバウンディングボックスを呼び出します。ポイントの場合、バウンディングボックスはバウンディングボックスとして取得されます。表面積と体積がゼロのボックス）、その辺は座標軸に平行です。

ノード分割プロセス

したがって、KD-Treeを使用する前に、構築する必要があります。 すべてのオブジェクトは、元のセットのオブジェクトを記述する1つの大きなバウンディングボックスに配置され（各オブジェクトはバウンディングボックスによって制限されます）、その後、その側面の1つに平行な平面で2つに分割（分割）されます。 2つの新しいノードがツリーに追加されます。 同様に、結果の平行六面体はそれぞれ2つに分割されます。 プロセスは、特別な基準（ SAHを参照）によって、またはツリーの特定の深さに到達したとき、またはツリーノード内で特定の数の要素に到達したときに終了します。 一部の要素は、左右のノードの両方に同時に入力できます（たとえば、三角形がツリー要素と見なされる場合）。



このプロセスを2Dの多くの三角形の例で説明します。









図1は、三角形の初期セットを示しています。 各三角形は独自の境界ボックスに配置され、三角形のセット全体が1つの大きなルート境界ボックスに内接します。









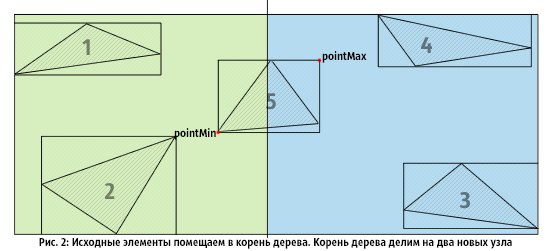
図2では 、ルートノードを2つのノード（OX） に分割します。三角形1、2、5は左ノードに、3、4、5は右ノードに分類されます。









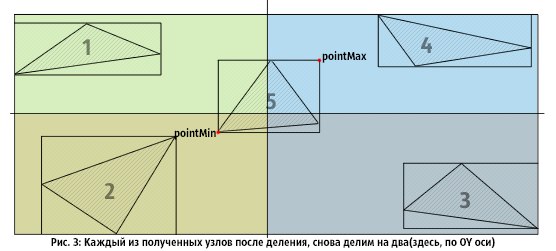
図3では、結果のノードが再び2つに分割され、それぞれに三角形5が含まれています。 プロセスが終了すると、4つのリーフノードが取得されます。



ツリーノードを分離する平面を選択することが非常に重要です。 これを行うには非常に多くの方法がありますが、実際には最も一般的な方法の一部のみを示します（初期オブジェクトは1つの大きな境界ボックスに配置され、座標軸の1つに平行に分離が行われると想定されています）：



⦁ 方法1 ：境界ボックスの最大の側面を選択します。 次に、割線平面が選択した辺の中央を通過します。



⦁ 方法2 ：中央値で分析：座標の1つですべてのプリミティブを並べ替え、並べ替えられたリストの中央にある要素（または要素の中心）を中央値と呼びます。 割線平面は中央値を通過するため、左右の要素の数はほぼ等しくなります。



⦁ 方法3 ：分割時に交互の辺を使用：深さ0で、OXに平行な辺の中央をビート、OYに平行な辺の中央を次の深さレベル、次にOZに沿ってビートなど 「すべての軸に沿って歩いた」場合、プロセスを再び開始します。 終了基準は上記で説明されています。



⦁ 方法4 ：最も「スマート」なオプションは、 SAH（Surface Area Heuristic）バウンディングボックスパーティション評価関数を使用することです。 （これについては以下で詳しく説明します）。 SAHは、ノード分割を停止するための普遍的な基準も提供します。



方法1と3は、ツリーの構築の速度に関しては優れています（側面の中央を見つけて平面を描くため、元のセット「左」と「右」の要素をふるい分けるのは簡単です）。 同時に、それらはしばしば空間のパーティションの大まかなビューを提供し、KDツリーの基本的な操作に悪影響を与える可能性があります（特にツリー内の光線を追跡する場合）。



方法2では、良い結果を得ることができますが、ノードの要素のソートに費やされるかなりの時間が必要です。 メソッド1、3と同様、実装は非常に簡単です。



最も興味深いのは、「スマート」SAHヒューリスティックを使用する方法（方法4）です。



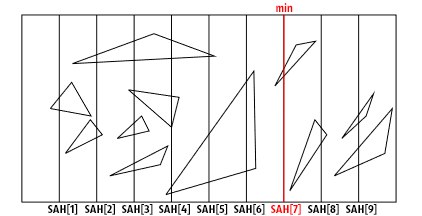
ツリーノードのバウンディングボックスは、N（軸に平行な）平面で各側でN + 1部分（通常は等しい）に分割されます（実際、各側面の平面の数は任意ですが、単純さと効率のために一定です） 。 さらに、平面と境界ボックスの可能な交差点で、特殊関数の値SAHが計算されます。 分割は、最小のSAH関数値を持つプレーンによって実行されます（次の図では、SAH [7]で最小値に達すると想定したため、このプレーンによって分割が実行されます（ただし、2D空間は非常に直接です））。











現在の平面の関数のSAH値は、次のように計算されます。











KD-Treeの実装では、各面を32のプレーンを使用して33の等しい部分に分割します。 したがって、テスト結果によると、ツリーの基本機能の「黄金の」中間速度/ツリーの構築速度を見つけることができました。



SAHヒューリスティックとして、上図に示されている関数を使用します。



決定を下すには、すべての割線面でこの関数の最小値のみが必要であることは注目に値します。 したがって、不等式の最も単純な数学的特性を使用し、ノード表面積（3D）（ SAR、SAL、SA ）を計算するときに2の乗算を破棄するだけでなく、この式を大幅に簡素化できます。 完全に、計算はノードごとに1回のみ実行されます：除算関数を終了するための基準を評価するとき。 このような単純な最適化により、ツリーの構築速度が大幅に向上します（ x2.5 ）。



SAH関数の値を効果的に計算するには、この平面の右側にある節点要素の数と左側にある節点要素の数をすばやく決定できる必要があります。 アルゴリズムとして2次漸近線を使用した粗い、いわゆるブルートフォースアプローチを使用すると、結果は不十分になります。 ただし、 「binned」メソッドを使用すると、状況は大幅に改善されます。 この方法の説明を以下に示します。



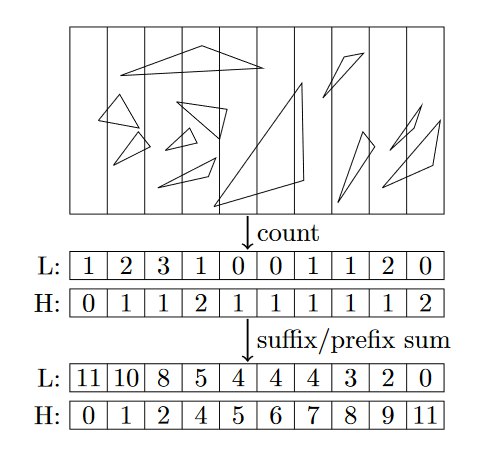
バウンディングボックス側をN個の等しい部分に分割し（プレーンの数は（N-1））、1組の座標（pointMin、pointMax- 図1を参照）でバウンディングボックスを格納し、ノードのすべての要素を1回パスすると仮定します。各プレーンについて、右側にある要素の数と、左側にある要素の数を正確に決定できます。 それぞれにN要素の2つの配列を作成し、ゼロで初期化します。 aHighおよびaLowという名前の配列とします。 ノードのすべての要素を連続して実行します。 現在の要素では、どの部分が境界ボックスのpointMinとpointMaxを取得するかを確認します。 したがって、セットの要素ごとに2つのインデックスを取得します。 iHigh （pointMaxの場合）およびiLow （pointMinの場合）という名前のインデックスとします。 その後、以下を実行します。aHigh[iHigh] + = 1、aLow [iLow] + = 1。



すべての要素を通過した後、塗りつぶされた配列aHighおよびaLowを取得します。 aHigh配列の場合、部分接尾辞（接尾辞）の量を計算し、aLowの場合、部分接頭辞（接頭辞）の量を計算します（図を参照）。 右側の要素の数（ そして右側のみ！ ）インデックスiの平面のaLow [i + 1]、左側にある要素の数（ そして左側のみ！ ）に等しいことがわかります ：AHigh [i]、として入力する要素の数左右のノード：AllElements-aLow [i + 1] -aHigh [i]。



この問題は解決され、この簡単なプロセスの例を以下に示します。











「ビート」プレーンの左右に所定の数の要素を取得すると、必要なメモリ量を事前に割り当てることができます（結局、最小SAHを受け取った後、すべての要素をもう一度調べて、それぞれを希望の配列に配置する必要があります） 、（および通常のpush_backを使用すると（予約が呼び出されなかった場合）一定のメモリ割り当てが非常に高価な操作になります）、ツリー構築アルゴリズム（x3.3）の速度にプラスの影響を与えます。



ここで、SAH計算式で使用される定数の目的をさらに詳しく説明し、このノードの分割を停止するための基準についても説明します。



定数cIおよびcTを調べると、より密なツリー構造（またはその逆）を達成でき、アルゴリズムの時間を犠牲にします。 主にレイトレーシングレンダリング用のKDツリーの構築に関する記事では、著者は値cI = 1、cT = [1; 2] ：cT値が高いほど、ツリーの構築が速くなり、そのようなツリーでのレイトレーシングの結果が悪化します。



私の実装では、ツリーを使用して「隣接」を検索し、必要な係数のテストと検索の結果に十分注意を払っています。cTの値が高いと、要素で完全に満たされていないノードが得られることがわかります。 この状況を回避するために、cT値を1に設定し、異なる大きなデータ単位でcI値をテストすることにしました。 その結果、建設中にかなりの時間を費やして、かなり密なツリー構造を得ることができました。 「隣人」の検索結果では、このアクションが積極的に反映され、検索速度が向上しました。



ノードの分割を停止するための基準は非常に簡単です。











つまり、子ノードのトレースのコストが親ノードのトレースのコストよりも大きい場合、分割を停止する必要があります。



KDツリーノードを分割する方法を学習したので、ノード内の要素の数が非常に多く、要素の数による停止基準によってアルゴリズムが無限になった初期のケースについて説明します。 実際には、画像へのすべての注意（たとえば、2Dの三角形）：











私はそのような状況を「扇形」と呼んでいます（共通の接点があり、一致するオブジェクトがあり、このカテゴリにも関連しています）。 割線面をどのように描画しても、中心点は何らかの方法でノードの1つに落ち、それによって共通点である三角形が表示されることがわかります。

ツリー構築プロセス

ツリーノードを分割する方法を学びましたが、今では、得られた知識をツリー全体の構築プロセスに適用することが残っています。 以下に、KD-Treeの構築の実装について説明します。



ツリーはルートから構築されます。 ツリーの各ノードには、左および右のサブツリーへのポインターを格納します。そのようなノードがない場合は、 リーフ （シート、つまり）と見なされます。 各ノードには、このノードのオブジェクトを記述する境界ボックスが保存されます。 リーフ（ そしてリーフのみ！ ）ノードには、このノードにあるオブジェクトのインデックスを格納します。 ただし、構築プロセス中に、ノードのメモリは部分的に割り当てられます（つまり、K個のノードにすぐに割り当てられます。第1に、メモリマネージャで作業する方が効率的です。第2に、アイテムの縮小はキャッシュに最適です）。 新しい要素をベクターに追加すると、別の場所にある既存のすべての要素のメモリが実装される可能性があるため、このようなアプローチではベクターにツリーノードを格納できません。



したがって、サブツリーへのポインターはすべての意味を失います。 タイプリスト（std ::リスト）のコンテナーを使用します。その各要素は、あらかじめ決められたサイズ（定数）のベクター（std ::ベクター）です。 （Open MPを使用して）マルチスレッドでツリーを構築します。つまり、各サブツリーを個別のスレッド（高速化のためにx4）で構築します。 コピーセマンティクス（C ++ 11）（+ 10％速度）の使用は、インデックスをリーフノードにコピーするのに理想的です。

KDツリー内のポイントへの「隣人」を見つける

したがって、ツリーが構築されました。KD-Treeでの検索操作の実装の説明に移りましょう。



三角形のセットで検索を実行するとします。点が与えられ、それに最も近い三角形を見つける必要があります。



ブルートフォースを使用して問題を解決するのは不利です。N個のポイントとM個の三角形のセットの場合、漸近的な動作はO（N * M）です。 さらに、アルゴリズムがポイントから三角形までの距離を「正直に」計算し、それを迅速に行うようにしたいと思います。



KDツリーを使用して、次のことを行います。



⦁ 手順1 。 このポイントに最も近いリーフノードを見つけます（各ノードでは、ご存知のように、境界ボックスを格納します。ノードの境界ボックスの中心までの距離（（pointMax + pointMin）* 0.5）を安全に計算できます）。



⦁ ステップ2 。 見つかったノード（nearestNode）のすべての要素を列挙することにより。 結果の距離はminDistで示されます。



⦁ ステップ3 。 開始点を中心とする半径と長さminDistの半径を作成します。 この球体が完全に内側にある（つまり、バウンディングボックスノードの側面の交点がない）かどうかを確認します。 存在する場合は、最も近い要素が見つかり、そうでない場合は、手順4に進みます。



⦁ 手順4 。 ツリーのルートから実行し、半径内の最も近い要素を検索します：ツリーを下って、右または左のノードが交差するかどうかを確認します（さらに、ノードは球内またはノード内の球内に完全に収まることができます...）。 ノードが交差している場合、同じノードの内部ノードに対して同様のチェックが実行されます。 リーフノードに到達した場合、このノード内のネイバーを徹底的に検索し、結果を球の半径の長さと比較します。 球の半径が見つかった距離よりも大きい場合、計算された最小値で球の半径の長さを更新します。 球体の更新された半径を使用してツリーでさらに下降します（再帰アルゴリズムを使用する場合、半径は参照によって関数に渡され、必要に応じて更新されます）。



次の図は、上記のアルゴリズムの本質を理解するのに役立ちます。











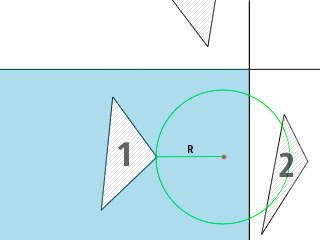
図によると ：この点に最も近い葉ノード（​​図の青）を見つけた（赤で強調表示されている）と仮定すると、ノード内の近傍を検索すると、これはインデックス1の三角形であることがわかりますが、これはそうではありません。 半径Rの円は隣接するノードと交差するため、このノードで検索し、新しく見つかった最小値と既存の最小値を比較する必要があります。 その結果、インデックス2の三角形が隣接していることが明らかになります。



ここで、「近くの」検索アルゴリズムで使用される中間操作の効果的な実装についてお話したいと思います。



ノード内の近隣を検索する場合、ポイントから三角形までの距離をすばやく計算できる必要があります。 最も簡単なアルゴリズムについて説明します。



三角形の平面上の点A（最も近くを探している点）の投影を見つけます。 見つかった点をPで示します。Pが三角形の内側にある場合、Aから三角形までの距離はセグメントAPの長さと等しくなります。そうでない場合は、Aから三角形の各辺（セグメント）までの距離を求めます。最小値を選択します。 問題は解決しました。



説明されているアルゴリズムは、最も効率的ではありません。 より効果的なアプローチは、特定のポイントから三角形の任意のポイントまでのすべての可能な距離を値とする関数の検索と分析（勾配の最小値の検出など）に依存します。 この方法は認識がやや複雑であり、私の意見では、別の記事に値します（これまでのところ、私のコードに実装されています。以下のコードへのリンクがあります）。 [1]による方法に慣れることができます。 テスト結果によると、この方法は先ほど説明した方法よりも10倍高速でした。



球が、境界ボックスで表される特定のノード内の点Oと半径Rの中心にあるかどうかを判断するのは簡単です（3D）：

inline bool isSphereInBBox(const SBBox& bBox, const D3& point, const double& radius) { return (bBox.m_minBB[0] < point[0] - radius && bBox.m_maxBB[0] > point[0] + radius && bBox.m_minBB[1] < point[1] - radius && bBox.m_maxBB[1] > point[1] + radius && bBox.m_minBB[2] < point[2] - radius && bBox.m_maxBB[2] > point[2] + radius); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

球体とノードのバウンディングボックスの交点、球体内のノードの位置、またはノード内の球体を決定するアルゴリズムでは、状況は多少異なります。 繰り返しますが、私は説明し（写真は[2]から取られました）、この手順を実行できる正しいコードを提供します（2D、3Dに類似）。

 bool intersects(CircleType circle, RectType rect) { circleDistance.x = abs(circle.x - rect.x); circleDistance.y = abs(circle.y - rect.y); if (circleDistance.x > (rect.width/2 + circle.r)) { return false; } if (circleDistance.y > (rect.height/2 + circle.r)) { return false; } if (circleDistance.x <= (rect.width/2)) { return true; } if (circleDistance.y <= (rect.height/2)) { return true; } cornerDistance_sq = (circleDistance.x - rect.width/2)^2 + (circleDistance.y - rect.height/2)^2; return (cornerDistance_sq <= (circle.r^2)); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最初の（最初の行のペア）4つの象限の計算を1つに減らします。 次の行のペアでは、円が緑の領域にあるかどうかを確認します。 存在する場合、交差点はありません。 次の数行は、円がパターンのオレンジまたはグレーの領域にあるかどうかを確認します。 進入すると、交差点が検出されます。



次に、円が長方形の角と交差するかどうかを確認する必要があります（次のコード行がこれを行います）。



実際、この計算は、中心が赤の領域内にあるすべての円に対して「false」を返し、中心が白の領域内にあるすべての円に対して「true」を返します。



一般に、このコードは必要なものを提供します（ここでは2Dのコードの実装を示しましたが、KD-Treeコードでは3Dバージョンを使用しています）。



検索アルゴリズムの速度についてだけでなく、KD-Treeでの検索速度が低下する重大な状況についても説明します。



前述のように、 「ファン」の状況ではノード内に多数の要素が生成され、要素が多いほど検索が遅くなります。 さらに、すべての要素が特定の点から等距離にある場合、検索はO（N） （球の表面にある点のセット、および球の中心に最も近いものを探します）で実行されます。 ただし、これらの状況が解消された場合、平均的な検索は、いくつかのノードの要素の列挙を持つツリー全体の下降に相当します。 Oを超える（log（N）） 。 検索の速度は、訪問したツリーのリーフノードの数に依存することは明らかです。



次の2つの図を検討してください。







これらの図の本質は、最も近い要素を探しているポイントがセットの元の境界ボックスから非常に遠くにある場合、半径minDist（最も近いものまでの距離）の半径の半径を持つ球は、同じ球体を検討しましたが、中心がセットの元の境界ボックスに非常に近い点にあります（当然、minDistは変わります）。 一般に、非常に遠いポイントへの近傍の検索は、元のセットの近くにあるポイントの検索よりも遅くなります。 私のテストでは、この情報を確認しました。

結果とまとめ

その結果、KD-Treeの実装についていくつかの言葉を追加して、結果を示したいと思います。 実際、元のセットの任意のオブジェクト（三角形、球体、点など）に簡単に適応できるように、コード設計が開発されました。 必要なことは、オーバーライドされた仮想関数を使用して継承クラスを作成することだけです。 さらに、私の実装では、特別なユーザー定義のSplitterクラスを渡すこともできます。 このクラス、またはその仮想分割メソッドは、切断面の正確な位置を決定します。 私の実装では、SAHに基づいて決定を下すクラスを提供します。 ここで、SAHに基づいてKDツリーの構築を加速することに焦点を当てた多くの記事では、ツリーの深さの初期値（一般に、ツリーノードの要素の数が大きい場合）の多くの著者は、切断面（中心または中央値による分割など） ）、およびSAHヒューリスティックは、ノード内の要素の数が少ないときにのみ適用されます。



私の実装にはそのようなトリックは含まれていませんが、それらをすばやく追加できます（新しいパラメーターでKD-Treeコンストラクターを展開し、必要な制限を制御して、目的のスプリッターで構築メンバー関数を呼び出すだけです）。 ツリー内の検索はマルチスレッドです。 すべての計算は倍精度の数値で実行されます。 ツリーの最大の深さは定数で設定されます（デフォルトは32）。 いくつかの#definesが定義されており、たとえば再帰なしで検索するときにツリーをトラバースできます（再帰を使用すると、終了する方が高速ですが、すべてのノードは特定のベクトルの要素です（つまり、メモリ内に近くにあります）。 コードと一緒に、テストデータセットを提供します（内部に異なる数の三角形（2から3,000,000）を持つ「修正OFF形式」の3Dモデル）。 ユーザーは、構築されたツリー（DXF形式）のダンプをスローし、対応するグラフィックプログラムで表示できます。 プログラムはまた、ツリー構築の品質をログに記録します（オン/オフできます）。ツリーの深さ、リーフノードの要素の最大数、リーフノードの要素の平均数、および操作時間がリセットされます。 結果の実装が理想的であると主張することはありませんが、それでも、私は見落とした場所を知っています（たとえば、テンプレートパラメータにアロケータを渡さない、Cコードが頻繁に存在する（ストリームを使用してファイルを読み書きしない） 、未検出のバグなどが考えられます。修正するときが来ました）。 そしてもちろん、ツリーは3D空間での作業用に厳密に作成および最適化されます。



次の特性を持つラップトップでコードをテストしました： Intel Core I7-4750HQ、4コア（8スレッド）2 GHz、RAM-8gb、Windows 10上のWin x64アプリ 。 SAH Iを計算するための係数は、 cT = 1.、cI = 1.5でした。 そして、結果について話すと、1、5百万であることがわかりました。 ツリーが1.5秒未満で構築される三角形。 2.4秒で300万 。 150万人。 ポイントと150万個の三角形（ポイントは元のモデルからそれほど遠くない）、検索は0.23秒で完了し、モデルからポイントが削除されると、時間は最大3秒になります。 300万ポイント（再び、モデルの近くにあります）と300万の三角形の場合、検索には約0.7秒かかります。 混乱しないことを願っています。 最後に、構築されたKDツリーの視覚化の図：

便利なリンク

[0] ： GitHubでのKDツリーの実装

[1] ： 点から三角形までの距離を検索します

[2] ： 円と長方形の交点の定義

[3] ： ウィキペディア上のKD-Treeの説明

[4] ： SAHに関する興味深い記事

[5] ： ray-tracing.ruでのKDツリーの説明