分析する場合

市場（Forexを含む）のフォーラムでは、2つのかなり安定した意見を区別できます。それらを悲観的で楽観的と呼びましょう。

悲観論者によると、市場は「ランダムなプロセスのスケジュールを作成し、友人（プロのトレーダー）がEURUSDチャートと区別できなかったため」です。つまり、市場で安定した収入を得ることは不可能です。

オプティミストはそれらに反対します。 市場がランダムである場合、相場は近所1を歩きませんが、無限に行きます。 したがって、市場はランダムではなく、それで稼ぐことができます。 利益率が大きい（もっとそう）本当に安定した収益戦略を見ました！

現実的であり、両方の意見から利益を得ようとしましょう：市場がランダムであると仮定し、この仮定に基づいて、トレーディングシステムの収益性の非ランダム性をチェックする方法論を構築します。

この記事で検討されている手法は、ファンド、外国為替、その他の市場に共通です。

問題の声明

真空中の球形馬についてのよく知られたジョークのおかげで、素晴らしいan話が生まれました。これは理想を意味しますが、実際のモデルではまったく適用できません。

それにもかかわらず、問題の正しい定式化により、「真空中の球体モデル」を適用することにより、かなり具体的な実際的な利点を引き出すことができます。たとえば、実際の学習対象の「球形性」の否定を通じて。

特定の市場で使用される取引システムがあるとします。また、市場がランダムではなく、システムが取引決定を行うための指標として偽装された乱数ジェネレーターではないものを使用するとします。収入の安定性を評価するために、利益因子を使用します。 $PF = {P \ over L}$ どこで

-収入額

-損失額（正の数）。

このシステムの安定性について話すために、利益要因は何ですか？明らかに、利益率が高いほど、システムを信頼する理由が多くなります。しかし、下限はさまざまな方法でさまざまな専門家によって推定されています。最も一般的なオプション：> 2（まあまあ）、> 5（良いシステム）、> 10（優れたシステム）。まだそのようなバリエーションがあります： $PF_m = {P-p_m \ L以上}$ どこで

-取引収入の最大値。この値は信頼できる利益率と呼ばれます。 1.6の信頼できる利益率の最小許容値と考えられています。

利益要因に常に悩まされたのは、市場のダイナミクスと貿易の激しさを考慮していないことです。したがって、利益因子の重要性を評価するための別のアプローチを提案します。事前に決められた事前の値と比較するのではなく、利益因子はできるだけ高くする必要がありますが 、同様の取引強度とボラティリティを持つランダム市場のランダムシステムの利益因子より低くはなりませんそれに応じて（実際、「理想的なガス」または「真空」における「球形のトレーダー」のそれより低くない）。

比較のために理想的なモデルを構築することだけが残っています。

「球状のトレーダー...」

ランダムな取引システム（「球状のトレーダー」）を検討しているとします。モデルはランダムであるため、取引イベントは以前の決定に関係なく、ランダムな時点で発生します。トランザクションの方向もランダムです（0.5の販売または購入の確率）。取引量は一定であり、一般性を損なうことなく、損益をポイント単位で推定すると想定しています。

平均トランザクション期間を

、および2つの後続のトランザクションのクローズ間の平均時間

（同時に開くトランザクションの数に制限を課しません）。

また、イベントのポアソンストリームを扱っているとします。

取引期間

は、指数分布の確率変数になります。

$f（t）= \ lambda_te ^ {-\ lambda_tt} \ \ \（1.1）$

どこで

。

取引数

一定期間コミット

ポアソン分布によって説明されます。

$P_T（k）= {{\左（\ lambda_ \ tau T \右）} ^ k \ over k！} E ^ {-\ lambda_ \ tau T} \ \ \（1.2）$

どこで

。

「...真空中」

ここで、「球状のトレーダー」、つまり「真空」、つまり完全にランダムな市場にとって理想的な環境を考えてみましょう。

相場の変化の正規分布によって市場が記述されていると仮定します

しばらくの間

：

$f（\ Delta）= {1 \ over \ sigma_T \ sqrt {2 \ pi}} e ^ {\ Delta ^ 2 \ over {2 \ sigma_T ^ 2}} \ \ \（2.1）$

どこで

次のように定義されます：分散を伴う正規分布確率変数により、単位時間にわたって引用符が変化するようにします

、その後、時間間隔を考慮すると

、引用符の変更に応じて、分散があります。

$\ sigma_T ^ 2 = \ sigma_1 ^ 2 T \ \ \（2.2）$

これは、ブラウンプロセスの既知の比率です。

式（2.1）および（1.1）を考慮すると、トランザクションの結果は、トランザクションの開始から終了までの期間にわたる見積もりの変化と見なされ、条件付き確率の積分として説明されます。

によって

：

$f _ {\ sigma_1、\ lambda_t}（\ Delta）= \ int \ limits_ {0} ^ {\ infty} {\ lambda_t \ over {\ sigma_1 \ sqrt {2 \ pi t}}} e ^ {-{\ Delta ^ 2 \ over {2 \ sigma_1 ^ 2 t}}} e ^ {-\ lambda_tt} dt$

または

$f _ {\ sigma_1、\ lambda_t}（\ Delta）= {\ lambda_t \ over {\ sigma_1 \ sqrt {2 \ pi}}} \ int \ limits_ {0} ^ {\ infty} t ^ {-{1 \ over 2}} e ^ {-{\ Delta ^ 2 \ over {2 \ sigma_1 ^ 2 t}}} e ^ {-\ lambda_tt} dt \ \ \（2.3）$

Wolfram Mathematicaを使用してこの積分を解くと、次の結果が得られます：

$f _ {\ sigma_1、\ lambda_t}（\ Delta）= {1 \ over \ sqrt {2}} {\ sqrt {\ lambda_t} \ over \ sigma_1} e ^ {-\ sqrt {2} {\ sqrt {\ lambda_t } \ over \ sigma_1} | \デルタ|}$

または

$f _ {\ sigma_1、\ lambda_t}（\ Delta）= {\ alpha \ over 2} e ^ {-\ alpha | \ Delta |} \ \ \（2.4）$

どこで $\ alpha = {\ sqrt {2 \ lambda_t} \ over \ sigma_1}$ 。

結果のパターンはラプラス分布です。

したがって、ランダム市場でのランダムシステムの1つのトランザクションの損益は、ラプラス分布と結果の絶対値によって記述されます。

トランザクションには指数分布があります。

$f_ \ alpha（R）= \ alpha e ^ {-\ alpha R} \ \ \（2.5）$

どこで $\ alpha = {\ sqrt {2 \ lambda_t} \ over \ sigma_1}$ 。

指数分布はカイ二乗分布の特殊なケースであることが知られています（

で

）これは、総収入と総損失がカイ二乗分布を持つランダム変数の合計として記述できることを意味します。つまり、それら自体がカイ二乗量であることを意味します。

やりましょう

結果のある有益な取引

そして

損失の絶対値で不採算

。それから総収入

（に正規化

）および合計損失

（同様に正規化

）は、自由度のあるカイ二乗分布によって記述されます

そして

したがって：

$f \左（P_ \ alpha \ right）= \ chi_ {k_p} ^ 2 \ left（{P_ \ alpha \ right）\ \ \（2.6）$

$f \左（L_ \ alpha \ right）= \ chi_ {k_l} ^ 2 \ left（{L_ \ alpha \ right）\ \ \（2.7）$

どこで $P_ \ alpha = {1 \ over {2 \ alpha}} \ sum \ limits_ {i = 1} ^ {k_p} R_i ^ +$ そして $L_ \ alpha = {1 \ over {2 \ alpha}} \ sum \ limits_ {i = 1} ^ {k_l} R_i ^-$ 。

これらの数量の比率は次のようになります。

${P_ \ alpha \ over {L_ \ alpha}} = {{{1 \ over {2 \ alpha}} \ sum \ limits_ {i = 1} ^ {k_p} R_i ^ +} \ over {{1 \ over { 2 \ alpha}} \ sum \ limits_ {i = 1} ^ {k_l} R_i ^-}} = {{\ sum \ limits_ {i = 1} ^ {k_p} R_i ^ +} \ over {\ sum \ limits_ {i = 1} ^ {k_l} R_i ^-}} = {P \ over L} = PF \ \ \（2.8）$

どこで $P = \合計\制限_ {i = 1} ^ {k_p} R_i ^ +$ 総収入 $L = \合計\制限_ {i = 1} ^ {k_l} R_i ^-$ 総損失。彼らの態度

-利益率。

次に、次の数量を検討します。

$PF_k = PF \回{k_l \ over {k_p}} \ \ \（2.9）$

この値は、「正規化された利益要因」、つまり取引ごとの平均損失に対する平均収入の比率として解釈できます。この数量の分布を見てみましょう：

$PF_k = PF \ times {k_l \ over {k_p}} = {P \ over L} \ times {k_l \ over {k_p}} = {{P_ \ alpha} \ over {L_ \ alpha}} \ times {k_l \ over {k_p}} = {{{P_ \ alpha} \ over {2k_p}} \ over {{L_ \ alpha} \ over {2k_l}}} \ \ \（2.10）$

得られた値、自由度の数に正規化された量のカイ2乗の比率は、フィッシャー分布を持ちます。

したがって、マグニチュードの分布、統計

既知の数の収益性がある「真空中の球形トレーダー」の利益要因

不採算

お得な情報。

未知の場合の一般化に進む前に

そして

、「完全にランダムではない」市場での「球形のトレーダー」の行動を考えてみましょう（この環境をジョークを「理想的なガス」と呼びましょう）。

「...完璧なガスの中」

次に、もう少し複雑な状況を考えてみましょう。市場が一般化されたブラウン運動である場合です。つまり、ランダムとは異なり、メモリがあります。この場合、式（2.2）は次の形式を取ります。

$\ sigma_T ^ 2 = \ sigma_1 ^ 2 T ^ {2H} \ \ \（3.1）$

どこで

-ハースト指数、時系列のフラクタル特性を特徴付ける値で、Hausdorff-Bezikovichフラクタル次元に関連

次のように：

。ハースト指数は値を取ることができます

。

で

時系列は、メモリを持たないランダムなものに縮退します。これは、上記で検討したケースに対応します。で

シリーズは、既存のトレンドの方向を変更するために絶えず努力しています。つまり、そのシリーズには記憶があります。で

シリーズには記憶もありますが、既存の傾向を維持しようと努力します;そのようなシリーズは永続的、決定論的と呼ばれます。ハースト指数が0.5と強く異なるほど、より明確なカオス的または決定論的な特性がシリーズで表現されます。

異なる市場は、ハースト指標の異なる値によって特徴付けられ、さらに、それらは時々変化する可能性があります。時系列の値からハースト指数を計算できます。したがって、利益率を評価するときは、値を考慮することができます

分析された戦略の取引が行われたのと同じ期間の多くの見積に基づいて計算されます。 RS統計やウェーブレットベースの方法など、ハースト指数を評価するためのいくつかの標準手順があります。

ランダム取引戦略がハーストインジケーターHを使用して市場で機能すると仮定し、（3.1）を考慮して、式（2.3）は次の形式を取ります。

$f _ {\ sigma_1、\ lambda_t、H}（\ Delta）= {\ lambda_t \ over {\ sigma_1 \ sqrt {2 \ pi}}} \ int \ limits_ {0} ^ {\ infty} t ^ {-H} e ^ {-{\ Delta ^ 2 \ over {2 \ sigma_1 ^ 2 t ^ {2H}}}} e ^ {-\ lambda_tt} dt \ \ \（3.2）$

明らかに、

この式は（2.3）と同等です。

残念ながら、分析形式の式（3.2）は統合されていません。したがって、Hurstインジケーターを使用した市場でのランダム取引の場合、取引の開始時と終了時の相場の差の絶対値の分布（取引の絶対結果）を見つける

数値モデリングを使用します。

Pythonを使用してシミュレーションを行いました。

モデリングは次のように実行されます

1）シミュレーションパラメーターを設定します。

-実験サンプルの量;

-ヒストグラムを構築するための範囲の数

2）指数分布したランダム変数のサンプルdistEと、ボリュームNの正規分布量のサンプルdistNをそれぞれ生成します。

3）関係（3.1 ）が与えられた場合、テストサンプルdistTを作成します。各サンプルの値は、distNとdistEの対応する値から計算されます。

4）結果の分布の場合、ヒストグラムはM個の範囲（範囲内のヒット数）から作成されます。得られたヒストグラムから、K個の最初の範囲が選択されます。ヒットの数はゼロではありません。また、最初の範囲のヒット数を正規化します。

5）得られたヒストグラムに基づいて、分布タイプが近似されます。

import matplotlib.pyplot as plt import numpy as np from scipy import stats def testH(N, M, H, p): distE = np.random.exponential(1, N) distN = np.random.normal(0, 1, N) distT = abs(distN * distE**H) if p == 1: plt.figure(1) plt.hist(distT, M) plt.title('H='+str(H)) [y, x] = np.histogram(distT, M) K = 0; for i in range(M): if y[i] > 0: K = i else: break y = y * 1.0 / y[0] x = x[1:K] y = y[1:K] return getCoeff(x, y, p, 'H='+str(H))

ハースト指数0.1、0.3、0.5、0.7、0.9について得られた分布のヒストグラムの例を以下に示します。

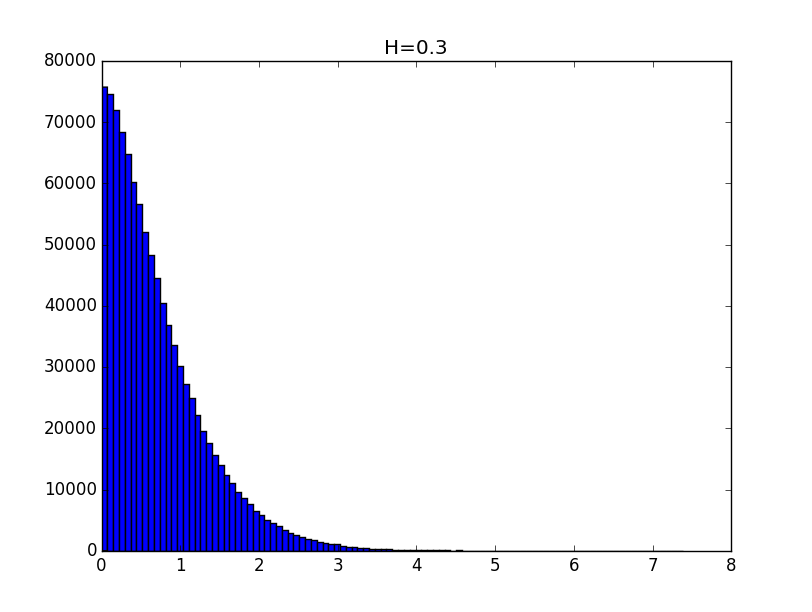
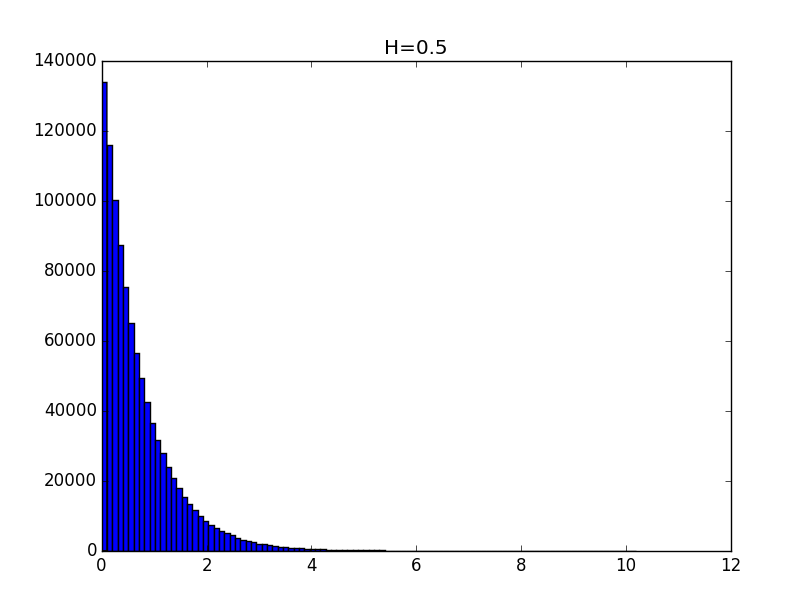
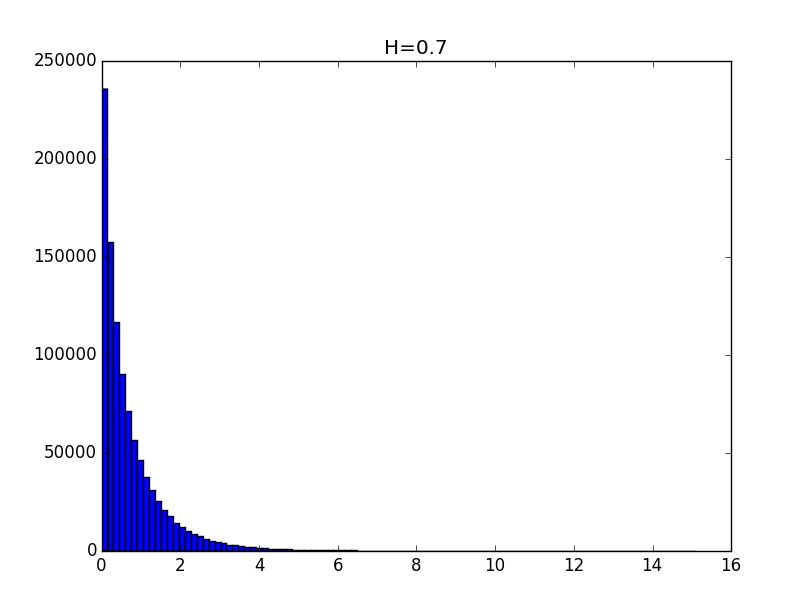
ヒストグラムの一般的な外観は、取得した分布が定数まで、次の形式の関数で記述できることを示しています。

$f _ {\ sigma_1、\ lambda_t、H}（\ Delta）= Ce ^ {-\ Delta ^ {K _ {\ sigma_1、\ lambda_t、H}}} \ \ \（3.3）$

分布パラメーターを検索するには、次のアルゴリズムを使用します。

1）与えましょう

-ヒストグラム範囲の重心

-最初の範囲のヒット数に正規化された範囲のヒット数。

2）次に、最初の範囲を無視して、変換を実行します。

そして

3）最小二乗法を使用して、線形回帰パラメーターを見つけます

そして

そのような

4）受信に基づいて

受け入れる：

。

パラメータ

正規化のエラーを補正します。

係数を計算する手順のリストを以下に示します。

 def getCoeff(x, y, p, S): X = np.log(x) Y = np.log(-np.log(y)) n = len(X) k = (sum(X) * sum(Y) - n * sum(X * Y)) / (sum(X) ** 2 - n * sum(X ** 2)) b = (sum(Y) - k * sum(X)) / n if p == 1: plt.figure(2) plt.plot(np.exp(X), np.exp(-np.exp(Y)), 'b', np.exp(X), np.exp(-np.exp(k * X + b)), 'r') plt.title(S) plt.show() return k

以下は、0.1、0.3、0.5、0.7、0.9のハースト値（青線）とそのモデル（赤線）のヒストグラムのエンベロープの例です。

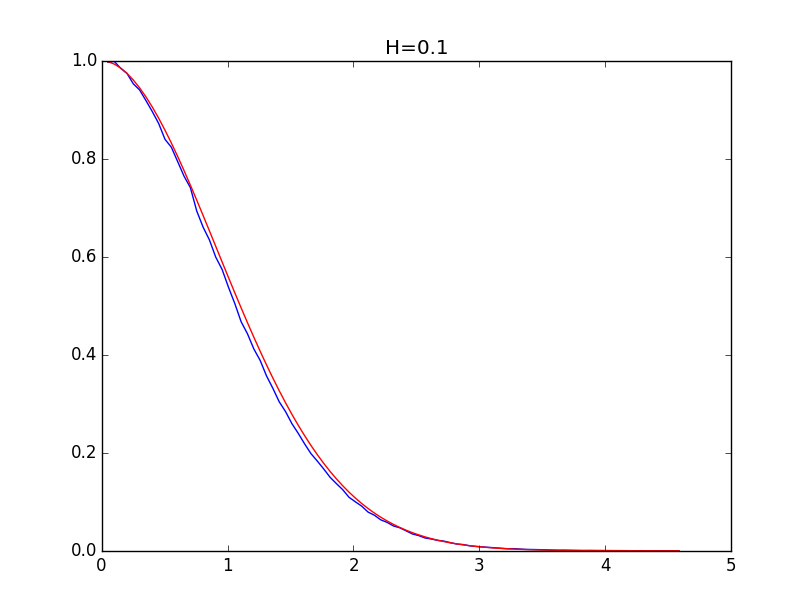
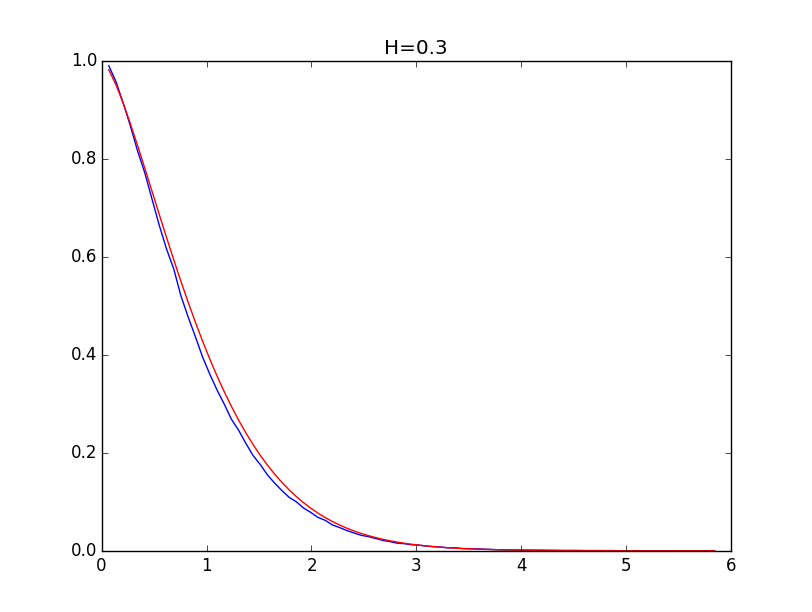
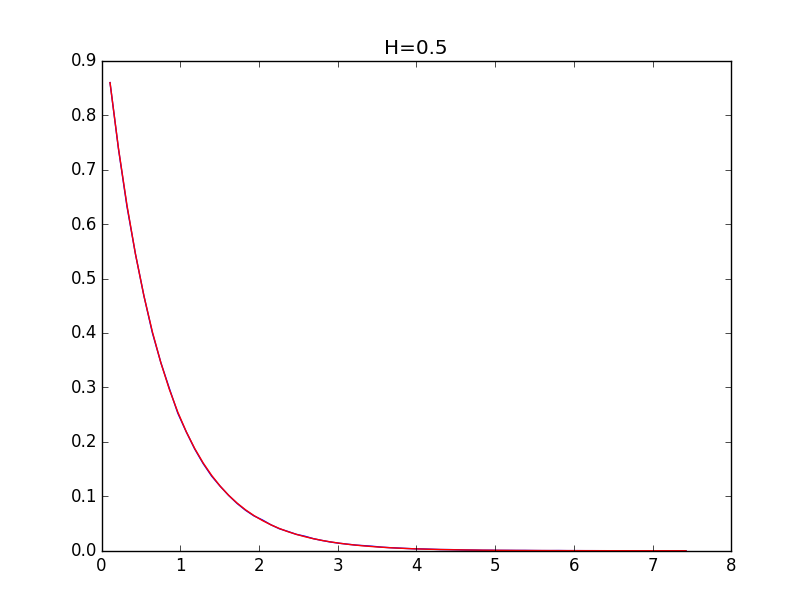
ハースト指数が0.5より大きい場合、モデリングの精度は高くなります。

今、依存関係を見つけます

から

。これを行うには、一連の値をシミュレートします

さまざまな

機能的な関係を確立しようとします。

値のモデル化に使用しました

0.01単位で0.01から0.99まで。また、各値に対して

値

20回計算され、平均されました。

 if __name__ == "__main__": N = 1000000; M = 100; Z = np.zeros((99, 2)) for i in range(99): Z[i, 0] = (i + 1) * 0.01 for j in range(20): W = float('nan') while np.isnan(W): W = testH(N, M, (i + 1) * 0.01, 0) Z[i, 1] += W Z[i, 1] *= 0.05 print Z[i, :] X = Z[:, 0].T Y = Z[:, 1].T plt.figure(1) plt.plot(X, Y) plt.show()

結果の依存関係の形式は次のとおりです。

グラフは歪んだシグモイドに似ているため、シグモイドの形のパターンも探します。

$K（H）= d-{c \ over b + e ^ {a_3 H ^ 3 + a_2 H ^ 2 + a_1 H + a_0}} \ \ \（3.4）$

最小二乗法による数値最小化手順により、次の結果が得られます。

合計2次誤差は約0.005です。

以下は実験依存のグラフです

（青い線）および式（3.4）によるモデル（赤い線）：

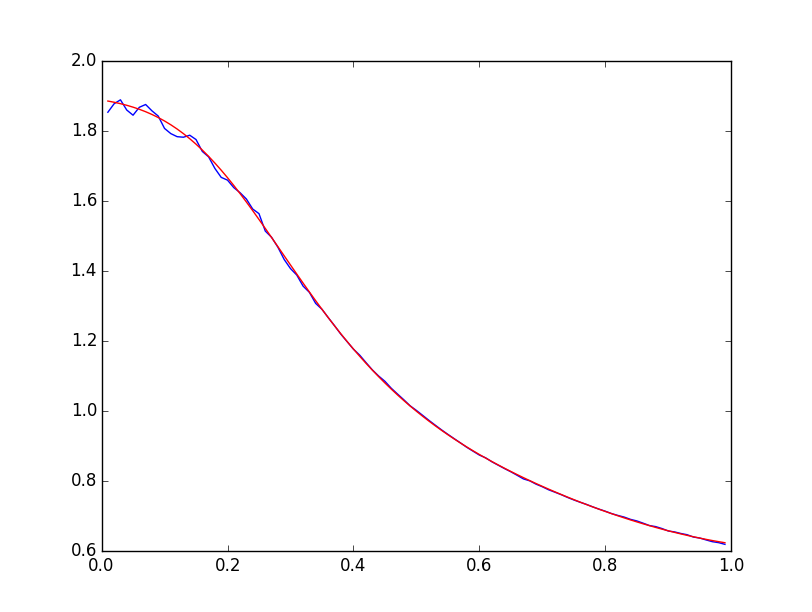
取得した規則性は、次の場合にのみ有効であることに注意してください。

そして

。したがって、将来これらの条件が満たされると見なし（それらの条件を確実に満たす）、対応するインデックスを省略します。

ここで、推定値について（3.3）および（3.4）を考慮に入れます

トランザクションの絶対値の分布を知っています。ランダム変数の変換の分布プロパティを使用して、（3.4）の変数を置き換えます。

次に：

$f_ {H}（\ Delta）= Ce ^ {-\ Delta ^ {K（H）}} >>> f '_ {H}（\ delta）= {C \ over K} \ delta ^ {{1 \ {K（H）}}-1} e ^ {-\ delta} \ \ \（3.6）$

これは、自由度の数を持つガンマ分布を持つ量の確率密度の関数です

スケールの単一パラメーター。これを前提に、式（3.6）。次のように書き換える必要があります。

$f '_ {H}（\ delta）= {1 \ over {\ Gamma \ left（{1 \ over {K（H）}} \ right）}} \ delta ^ {{1 \ over {K（H） }}-1} e ^ {-\ delta} \ \（3.7）$

中間結果を要約するには：

マーケットハースト情報を持つ

システムをテストするのと同じ履歴の期間について計算すると、値を見つけることができます

式（3.4）を使用します。平均取引強度も見つけることができます。

およびパラメーター

トランザクション結果用。上記で提案した式が真になるためには、値を与える必要があります

そして

ユニットに。これを行うために、正規化を実行します。

どこで

-結果

トランザクション（結果の符号に関係なく）。この変換は（3.1）から始まります。

（3.7）によると、数量

パラメータ付きのガンマ分布を持つ

。したがって、数量

カイ二乗分布 c

自由度。

やりましょう

収入価値のある収益性の高い取引

そして

損失を伴う

（正の値）。次に、検討

および（3.7）、数量

$P_H = 2 \合計\制限_ {i = 1} ^ {k_P} {（R_i ^ +）} ^ {K（H）}$

そして

$L_H = 2 \合計\制限_ {i = 1} ^ {k_L} {（R_i ^-）} ^ {K（H）}$

自由度の量を持つカイ二乗分布を持つ

そして

それに応じて。

したがって、値：

$PF_H = {P_H \ over {L_H}} \回{k_L \ over {k_P}} = {{\ sum \ limits_ {i = 1} ^ {k_P} {（R_i ^ +）} ^ {K（H）} } \以上{\合計\制限_ {i = 1} ^ {k_L} {（R_i ^-）} ^ {K（H）}}} \回{k_L \ over {k_P}} \ \ \（3.8）$

フィッシャー分布c

自由度（一般的な場合、自由度の数は非整数になるため、市場のフラクタル特性が現れます）。

値と呼ぶ

正規化された一般的な利益率。で

一般化された利益因子は、私たちに馴染みのある正規化された利益因子に縮退します（2.9）。

最終的な一般化

そこで、ランダムな市場で「球状のトレーダー」を調べ、正規化された利益率の分布を見つけました。次に、結果は、測定可能な量であるハースト指数で表される任意のフラクタル次元を持つ市場の場合に一般化されました。

これで、一般化正規化利益係数と呼ばれる値が得られました。これは、トランザクションの結果に関する情報を使用して計算されます（ちなみに、スプレッドを考慮するために調整することを忘れないでください：損失から減算して収入に加算します）。方法論の汎用性を高めるために、トランザクションの量は一定と見なされるか、すべてをポイントで測定します。平均トランザクション期間とトランザクション結果の分布の標準偏差を正規化することを忘れないでください。

どこで

-結果

お得な情報。

現時点で得られたすべての結果は、既知の数の収益性のある取引と損失を生じさせる取引に結び付けられています。これは、既知の合計取引数の二項分布を持つランダム変数であり、ポアソンに従って分布するランダム変数でもあります。

新しい表記法を紹介します。与えられた収益性のある数に対する一般化された正規化された利益係数（3.8）

そして不採算の量

取引（既知のハーストインジケーター

）は

自由度のあるフィッシャー分布を持ちます

。

次に、収益性のある取引と損失を伴う取引の数の二項分布、および各取引で収益または損失を発生させる可能性を考慮して、値を導入します

-トランザクションの合計数のみを考慮した一般化された正規化された利益率。この値には、次の分布があります。

$F_N（PF_ {H、N}）= \左（{1 \ over 2} \右）^ N \ sum \ limits_ {k = 0} ^ {N} {\ left [{N！\ Over {k！（ Nk）！}} F_ {2kK（H）、2（Nk）K（H）}（PF_ {H、N}）\右]} \ \ \（4.1）$

どこで

-自由度のあるフィッシャー分布密度

そして

、および値

式（3.4）で記述されます。

-ハーストインジケータ。

実際には、十分に大きい

式（4.1）は不完全な合計で近似できます。

$F_N（PF_ {H、N}）= {\ sum \ limits_ {k = a} ^ {b} {\ left [{N！\ Over {k！（Nk）！}} F_ {2kK（H）、2 （Nk）K（H）}（PF_ {H、N}）\ right]} \ over {\ sum \ limits_ {k = a} ^ {b} {N！\ Over {k！（Nk）！}} }} \ \ \（4.1 *）$

どこで

そして

（

）収益性の高い取引数の可能な値の特定のサブセットを制限します。

ここで、トランザクションの数を参照せずに、一般的な正規化された利益要因を考慮しますが、平均取引強度のみを考慮します

および戦略テスト期間

：

。トランザクションの総数がポアソンによって分配されるとすると、

次の分布になります。

$PF _ {\ lambda_ \ tau、T、H} = \ sum \ limits_ {k = 0} ^ \ infty {{\ left（\ lambda_ \ tau T \ right）^ k \ over {k！}} F_k（PF_ { H、N}）} \ \ \（4.2）$

または、範囲内の考慮されたトランザクション数について

：

$PF _ {\ lambda_ \ tau、T、H} = {\ sum \ limits_ {k = a} ^ b {{\ left（\ lambda_ \ tau T \ right）^ k \ over {k！}} F_k（PF_ { H、N}）} \ over {\ sum \ limits _ {k = a} ^ b {\ left（\ lambda_ \ tau T \ right）^ k \ over {k！}}}} \ \ \（4.2 * ）$

結果の分布を使用して、既知の平均取引期間と既知のボラティリティとハーストインジケーターを持つ既知の市場時間の取引強度で（3.8）に従って計算された一般化正規化利益因子の有意性を検証できます。テストアプリケーションの方法論は、フィッシャーテストの場合とまったく同じです。それを実行するには、密度関数を（4.1）（または（4.1 *））でフィッシャー分布関数に置き換え、計算された一般化利益因子の値を引数として置き換えるだけで十分です。得られた確率値は値と比較する必要があります

どこで

-重要度のレベルが必要です。このレベルを超えた場合、計算された統計は、取引システムのランダム性に関する仮説（「真空中のトレーダーの球形性」）を拒否する可能性があります。

おわりに

この仕事で提案されたアプローチは、市場のボラティリティとフラクタル特性、ならびに取引の強度とトランザクションの平均期間を考慮に入れた一般化された正規化された利益因子の構築に基づいて、ランダムな方法で同様の結果を得る確率に関して達成された結果の有意性の統計的テストを構築することを可能にします。テストを使用すると、システムの信頼性を示すために必要な条件を満たしていることについて、特定の重要度で話すことができます。しかし、得られた結果は十分な条件ではありません...

残念ながら、私はテストを知りません。その結果は、確かに信頼できる戦略を明確に採用するのに十分です。

「真空中の球状のトレーダー」：使用説明書