コードの最適化：メモリ

ほとんどのプログラマは、コンピューティングシステムを、命令を実行するプロセッサ、およびプロセッサの命令とデータを保存するメモリと考えています。 この単純なモデルでは、メモリはバイトの線形配列で表され、プロセッサはメモリ内のどこにでも一定時間でアクセスできます。 これはほとんどの状況で効果的なモデルですが、最新のシステムが実際にどのように機能するかを反映していません。



実際、メモリシステムは、容量、コスト、アクセス時間が異なるストレージデバイスの階層を形成します 。 プロセッサレジスタには、最も一般的に使用されるデータが格納されます。 プロセッサの近くにある小さな高速キャッシュは、比較的低速のRAMにあるデータの一部を格納するバッファゾーンとして機能します。 RAMは、低速のローカルドライブのバッファーとして機能します。 また、ローカルドライブは、ネットワークで接続されたリモートマシンからのデータのバッファーとして機能します。









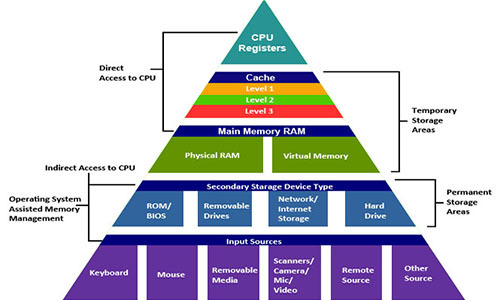
よく書かれたプログラムは、下位レベルのストアよりも特定レベルのストアに頻繁にアクセスする傾向があるため、メモリ階層が機能します。 したがって、低レベルのストレージは、より遅く、大きく、安価になります。 その結果、大量のメモリを取得します。これは、階層の最下部でストレージのコストがかかりますが、階層の最上部で高速ストレージの速度でプログラムにデータを配信します。



プログラマーとしては、メモリーの階層を理解する必要があります。これは、プログラムのパフォーマンスに大きく影響するためです。 システムがデータを階層内で上下に移動する方法を理解している場合、プロセッサがデータに高速にアクセスできるように、データを階層の上位に配置するプログラムを作成できます。



この記事では、ストレージデバイスが階層構造でどのように編成されているかを説明します。 特に、プロセッサとRAMの間のバッファゾーンとして機能するキャッシュメモリに集中します。 プログラムのパフォーマンスに最も大きな影響を与えます。 ローカリティの重要な概念を紹介し、 ローカリティのプログラムを分析する方法を学び、また、プログラムのローカリティを高めるのに役立つテクニックを学びます。



この記事は、「 コンピューターシステム：プログラマーの視点」の第6章に触発されました。 このシリーズの別の記事「コードの最適化：プロセッサ」では 、プロセッササイクルについても戦います。

記憶も重要

行列の要素を要約する2つの関数を考えます。 それらはほとんど同じです。最初の関数のみが行列の要素を行ごとにバイパスし、2番目の関数は列単位でバイパスします。

int matrixsum1(int size, int M[][size]) { int sum = 0; for (int i = 0; i < size; i++) { for (int j = 0; j < size; j++) { sum += M[i][j]; //   } } return sum; } int matrixsum2(int size, int M[][size]) { int sum = 0; for (int i = 0; i < size; i++) { for (int j = 0; j < size; j++) { sum += M[j][i]; //    } } return sum; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

両方の機能は、同じ数のプロセッサ命令を実行します。 ただし、 Core i7 Haswellを搭載したマシンでは、最初の関数は大きな行列に対して25倍高速です。 この例は、 メモリも重要であることをよく示しています 。 実行する命令の数に関してのみプログラムの有効性を評価する場合、非常に遅いプログラムを作成できます。



データには、 localityと呼ばれる重要なプロパティがあります。 データに取り組んでいるとき、それらが近くのメモリにあることが望ましいです。 行列が行ごとにメモリに保存されるため、列ごとに行列をバイパスすると局所性が低下します。 以下に地域性について説明します。

記憶の階層

最新のメモリシステムは、高速の小さなタイプのメモリから低速の大きなタイプのメモリまでの階層を形成します。 特定の階層レベルは、より低いレベルにあるデータのキャッシュまたはキャッシュです。 これは、下位レベルのデータのコピーが含まれることを意味します。 プロセッサがデータを受信する場合、最初に最高速で検索します。 そして、それが見つからない場合は、下位のものに下がります。



階層の最上部にはプロセッサレジスタがあります。 それらへのアクセスには0の手段が必要ですが、それらの数はわずかです。 次に、数キロバイトの第1レベルのキャッシュがあり、アクセスには約4クロックサイクルかかります。 その後、数百キロバイトの低速なセカンドレベルキャッシュが追加されます。 次に、数メガバイトのL3キャッシュ。 それはずっと遅いですが、それでもRAMより速いです。 次は比較的遅いRAMです。



RAMは、ローカルディスクのキャッシュと見なすことができます。 ディスクはストレージデバイスの主力製品です。 それらは大きく、遅く、安価です。 コンピューターは、ファイルを処理するときに、ディスクからRAMにファイルをロードします。 RAMとドライブ間のアクセス時間のギャップは膨大です。 ドライブはRAMよりも数万倍遅く、一次キャッシュよりも数百倍遅いです。 ディスクを1回使用するよりもRAMを数千回使用する方が有利です。 この知識は、 Bツリーなどのデータ構造に基づいています。Bツリーは 、RAMにより多くの情報を配置し、ディスクへのアクセスを一切回避しようとします。



ローカルディスク自体は、リモートサーバーにあるデータのキャッシュと見なすことができます。 ウェブサイトにアクセスすると、ブラウザはウェブページの画像をディスクに保存するため、再度アクセスするときにダウンロードする必要はありません。 メモリの下位階層があります。 Googleなどの大規模なデータセンターでは、大量のデータをテープに保存します。これらのデータは倉庫のどこかに保存され、必要に応じて手動またはロボットで接続する必要があります。



最新のシステムには、ほぼ次の特性があります。

キャッシュタイプ	アクセス時間（ティック）	キャッシュサイズ
登録	0	数十個
L1キャッシュ	4	32 KB
L2キャッシュ	10	256 KB
L3キャッシュ	50	8 MB
RAM	200	8 GB
ディスクバッファ	100'000	64 MB
ローカルディスク	10'000'000	1000 GB
リモートサーバー	1'000'000'000	∞

高速メモリは非常に高価であり、低速メモリは非常に安価です。 システム設計者にとって、低速で安価なメモリの大きなサイズと高速で高価な小さなサイズを組み合わせるのは素晴らしいアイデアです。 したがって、システムは高速のメモリ速度で実行でき、コストがかかります。 それがどのように機能するかを見てみましょう。



コンピューターに8 GBのRAMと1000 GBのディスクがあるとします。 ただし、ディスク上のすべてのデータを一度に処理しているわけではないと考えてください。 オペレーティングシステムをロードし、Webブラウザー、テキストエディター、他のいくつかのアプリケーションを開いて、数時間それらを操作します。 これらのアプリケーションはすべてRAMに配置されるため、システムがディスクにアクセスする必要はありません。 次に、もちろん、1つのアプリケーションを閉じてから別のアプリケーションを開きます。これをディスクからRAMにロードする必要があります。 ただし、数秒かかり、その後、ディスクにアクセスせずにこのアプリケーションを数時間使用します。 一時的にRAMにキャッシュされている少量のデータのみで作業しているため、実際に遅いディスクに気付くことはありません。 ディスク全体の内容をロードできる1024 GBのRAMのインストールに多額の費用をかける必要はありません。 これを行った場合、仕事の違いにほとんど気付かないでしょう、それは「お金を無駄遣いする」でしょう。



これは、小さなプロセッサキャッシュの場合にも当てはまります。 int型の1000個の要素を含む配列で計算を実行する必要があるとします。 このようなアレイは4 KBを占有し、32 KBの第1レベルキャッシュに完全に収まります。 システムは、特定のRAMで作業を開始したことを理解しています。 このピースをキャッシュにコピーし、プロセッサーはこのアレイで操作をすばやく実行し、キャッシュの速度を享受します。 次に、キャッシュから変更された配列がRAMにコピーされます。 キャッシュの速度を上げるためにRAMの速度を上げても、目に見えるパフォーマンスの向上は得られませんが、システムのコストは数百、数千倍になります。 しかし、これらすべては、プログラムのローカリティが良好な場合にのみ当てはまります。

局所性

局所性は、この記事の基本概念です。 原則として、ローカリティが良好なプログラムは、ローカリティが低いプログラムよりも速く実行されます。 局所性には2つのタイプがあります。 メモリ内の同じ場所に何度もアクセスすると、これは一時的な場所になります。 データにアクセスし、元のメモリの隣にある他のデータを参照する場合、これは空間的局所性です 。



配列の要素を合計するプログラムを考えてみましょう。

 int sum(int size, int A[]) { int i, sum = 0; for (i = 0; i < size; i++) sum += A[i]; return sum; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このプログラムでは、ループの各反復でsumおよびi変数にアクセスします。 それらは良好な時間的局所性を持ち、高速プロセッサレジスタに配置されます。 配列Aの要素は、各要素に1回しかアクセスしないため、時間的な局所性が不十分です。 しかし、その後、彼らは良い空間的局所性を持っています-1つの要素に触れた後、その隣の要素に触れます。 このプログラムのすべてのデータは、良好な時間的局所性または良好な空間的局所性を持っているため、プログラムは一般的に良好な局所性を持っていると言います。



プロセッサがメモリからデータを読み取るとき、キャッシュから他のデータを削除しながら、キャッシュにデータをコピーします。 彼がトピックを削除するために選択するデータは複雑です。 しかし、その結果、一部のデータに頻繁にアクセスすると、キャッシュに残る可能性が高くなります。 これは、時間的局所性の利点です。 プログラムは、より少ない変数で作業し、より頻繁にアクセスする方が適切です。



階層レベル間のデータ移動は、特定のサイズのブロックによって実行されます。 たとえば、 Core i7 Haswellプロセッサは、64バイトのブロックでキャッシュ間でデータを移動します。 特定の例を考えてみましょう。 上記のプロセッサを搭載したマシンでプログラムを実行します。 long型の8バイト要素を含むv配列があります。 そして、この配列の要素をループで順番にループします。 v [0]を読み取るとき、キャッシュにはありません。プロセッサは、RAMから64バイトのブロックでキャッシュに読み取ります。 つまり、要素v [0] -v [7]がキャッシュに送信されます。 次に、要素v [1] 、 v [2] 、...、 v [7]を巡回します。 それらはすべてキャッシュ内にあり、すぐにアクセスできます。 次に、キャッシュにない要素v [8]を読み取ります。 プロセッサは、要素v [8] -v [15]をキャッシュにコピーします。 これらの要素をすばやく調べますが、キャッシュ内でv要素を見つけることができません[16] 。 などなど。



したがって、メモリからいくつかのバイトを読み取り、それらの隣のバイトを読み取る場合、おそらくキャッシュにあります。 これが空間的局所性の利点です。 近くのメモリにあるデータを操作するには、計算の各段階で努力する必要があります。



配列を順番に走査し、要素を1つずつ読み取ることをお勧めします。 マトリックスの要素をバイパスする必要がある場合は、列ではなく行ごとにマトリックスを走査することをお勧めします。 これにより、空間的な局所性が向上します。 これで、 matrixsum2関数がmatrixsum1関数よりも遅い理由を理解できます。 2次元配列は、メモリ内の行ごとに配置されます。最初の行は最初に配置され、2番目の行の直後に配置されます。 最初の関数は、1つの大きな1次元配列をバイパスするかのように、行列要素を行ごとに読み取り、メモリ内を順番に移動します。 この関数は、主にキャッシュからデータを読み取ります。 2番目の関数は行から行へと進み、一度に1つの要素を読み取りました。 彼女は記憶から左から右へジャンプし、最初に戻って再び左から右へジャンプし始めたようでした。 各反復の終了時に、最後の行でキャッシュが詰まったため、次の反復の開始時にキャッシュは最初の行を見つけられませんでした。 この関数は、主にRAMからデータを読み取ります。

キャッシュフレンドリーなコード

プログラマーとして、 キャッシュに 優しいと言われているコードを書くようにしてください。 原則として、大部分の計算はプログラム内の数箇所でのみ実行されます。 通常、これらはいくつかの重要な機能とサイクルです。 ネストされたループがある場合、コードは最も頻繁に実行されるため、最も内側のループに注意を向ける必要があります。 これらのプログラムの場所は、地域性を改善するために最適化する必要があります。



マトリックス計算は、信号解析アプリケーションおよび科学計算で非常に重要です。 プログラマーのタスクが行列乗算関数を作成することである場合、99.9％が次のように書き込みます。

 void matrixmult1(int size, double A[][size], double B[][size], double C[][size]) { double sum; for (int i = 0; i < size; i++) for (int j = 0; j < size; j++) { sum = 0.0; for (int k = 0; k < size; k++) sum += A[i][k]*B[k][j]; C[i][j] = sum; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このコードは、行列乗算の数学的な定義を逐語的に繰り返します。 最終マトリックスのすべての要素を行ごとに調べ、それぞれを1つずつ計算します。 コードには1つの非効率性があります。これは、最も内側のループの式B [k] [j]です。 列で行列Bを巡回します。 それについては何もできないように思われ、妥協する必要があります。 しかし、方法があります。 同じ計算を別の方法で書き換えることができます。

 void matrixmult2(int size, double A[][size], double B[][size], double C[][size]) { double r; for (int i = 0; i < size; i++) for (int k = 0; k < size; k++) { r = A[i][k]; for (int j = 0; j < size; j++) C[i][j] += r*B[k][j]; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

この関数は非常に奇妙に見えます。 しかし、彼女はまったく同じことをします。 最終マトリックスの各要素を一度に計算するのではなく、各反復で部分的に要素を計算するようです。 しかし、このコードの重要な特性は、内側のループで両方の行列を行ごとにループすることです。 Core i7 Haswellを搭載したマシンでは、 2番目の関数は大きなマトリックスに対して12倍高速に動作します。 このようにコードを整理するには、本当に賢明なプログラマーである必要があります。

ブロッキング

ブロッキングと呼ばれるテクニックがあります。 すべてが高レベルのキャッシュに収まらない大量のデータに対して計算を実行する必要があるとします。 このデータを小さなブロックに分割し、各ブロックをキャッシュします。 これらのブロックに対して個別に計算を実行し、結果を組み合わせます。



これを例で示すことができます。 隣接行列として表される有向グラフがあるとします。 これはゼロと1の正方行列であるため、インデックス（i、j）の行列要素が1に等しい場合、グラフiの頂点から頂点jまでの面があります。 この指向グラフを非指向グラフに変えたいと思います。 つまり、面（i、j）がある場合、反対側の面（j、i）が表示されます。 行列を視覚化する場合、要素（i、j）と（j、i）は対角線に関して対称であることに注意してください。 この変換は、コードに簡単に実装できます。

 void convert1(int size, int G[][size]) { for (int i = 0; i < size; i++) for (int j = 0; j < size; j++) G[i][j] = G[i][j] | G[j][i]; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ブロッキングは自然に現れます。 大きな正方行列を想像してください。 次に、この行列を水平線と垂直線で切り取り、たとえば16の等しいブロック（4行4列）に分割します。 任意の2つの対称ブロックを選択します。 あるブロック内のすべての要素には、別のブロック内に独自の対称要素があることに注意してください。 これは、これらのブロックに対して同じ操作を順番に実行できることを示唆しています。 この場合、各段階で2つのブロックのみで作業します。 ブロックを十分に小さくすると、高レベルのキャッシュに収まります。 このアイデアをコードで表現してください：

 void convert2(int size, int G[][size]) { int block_size = size / 12; //   12*12  // ,     for (int ii = 0; ii < size; ii += block_size) { for (int jj = 0; jj < size; jj += block_size) { int i_start = ii; //  i     [ii, ii + block_size) int i_end = ii + block_size; int j_start = jj; //  j     [jj, jj + block_size) int j_end = jj + block_size; //   for (int i = i_start; i < i_end; i++) for (int j = j_start; j < j_end; j++) G[i][j] = G[i][j] | G[j][i]; } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ブロッキングは、優れたプリフェッチを実行する強力なプロセッサを備えたシステムのパフォーマンスを改善しないことに注意してください。 プリフェッチしないシステムでは、ブロッキングによりパフォーマンスが大幅に向上します。



Core i7 Haswellプロセッサを搭載したマシンでは、 2番目の機能は高速ではありません。 より単純なPentium 2117Uプロセッサを搭載したマシンでは、 2番目の機能は2倍高速です。 プリフェッチしないマシンでは、生産性がさらに向上します。

より高速なアルゴリズム

アルゴリズムのコースからは、誰もが最小の複雑さで良いアルゴリズムを選択し、高い複雑さで悪いアルゴリズムを避ける必要があることを知っています。 しかし、これらの困難は、私たちの考えによって作成された理論的なマシンでのアルゴリズムの実行を評価します。 実際のマシンでは、理論的に悪いアルゴリズムは、理論的に良いアルゴリズムよりも速く実行できます。 RAMからのデータの取得には200サイクルかかり、最初のレベルのキャッシュからは4サイクル-50倍高速であることを思い出してください。 良いアルゴリズムがメモリに頻繁にアクセスし、悪いアルゴリズムがキャッシュにデータを配置する場合、良いアルゴリズムは悪いアルゴリズムよりも実行速度が遅くなります。 また、良いアルゴリズムは、悪いアルゴリズムよりもプロセッサー上で動作が悪い場合があります。 たとえば、優れたアルゴリズムはデータに依存し、プロセッサパイプラインをロードできません。 そして、悪いアルゴリズムはこの問題を奪われ、各サイクルでパイプラインに新しい命令を送ります。 つまり、アルゴリズムの複雑さだけではありません。 特定のデータを使用して特定のマシンでアルゴリズムを実行する方法が重要です。



整数のキューを実装する必要があり、新しい要素をキュー内の任意の位置に追加できると想像してください。 配列とリンクリストの2つの実装から選択します。 配列の中央に要素を追加するには、配列の右半分にシフトする必要がありますが、これには直線的な時間がかかります。 リストの中央にアイテムを追加するには、リストを中央に移動する必要がありますが、これも直線的な時間がかかります。 彼らは同じ困難を抱えているので、リストを選ぶ方が良いと思います。 さらに、リストには1つの優れたプロパティがあります。 リストは制限なく拡大できます。配列がいっぱいになると、配列を拡張する必要があります。



両方の方法で1000要素のキューを実装するとします。 そして、キューの中央に要素を挿入する必要があります。 リストアイテムはメモリ全体にランダムに散らばっているので、500アイテムをバイパスするには、500 * 200 = 100'000メジャーが必要です。 配列はメモリ内に順番に配置されるため、一次キャッシュの速度を楽しむことができます。 いくつかの最適化を使用して、要素ごとに1〜4サイクルを費やして、配列の要素を移動できます。 最大500 * 4 = 2000サイクルでアレイの半分をシフトします。 それは50倍高速です。



前の例ですべての追加がキューの先頭にある場合、リンクリストを使用した実装の方が効率的です。 追加の一部がキューの中央にある場合、配列の実装がより適切な選択になる可能性があります。 一部の操作にはタクトを費やし、他の操作にはタクトを保存します。 そして最終的に、彼らは勝ったかもしれません。

おわりに

メモリシステムは、階層の最上部に小さくて高速なデバイス、下部に大きくて遅いデバイスを持つストレージデバイスの階層として編成されます。 局所性の良いプログラムは、プロセッサキャッシュからのデータを処理します。 ローカリティの低いプログラムは、比較的遅いRAMのデータを処理します。



メモリー階層の性質を理解しているプログラマーは、データを階層内で可能な限り高く配置し、プロセッサーがそれをより速く受信するようにプログラムを構成できます。



特に、次の手法が推奨されます。

• 内側のサイクルに注意を向けてください。 最大量の計算とメモリアクセスが発生するのはそこです。
• オブジェクトをメモリ内にある順番で順番にメモリから読み取ることにより、空間的な局所性を最大化してください。
• データオブジェクトをメモリから読み取った後、できる限り頻繁に使用して、一時的な局所性を最大化してください。