量子システムが大きく変化する可能性がある分野の1つは、デジタル署名メカニズムです。 このレポートは、古典的なコンピューターのアナログよりも根本的に優れているハッシュアルゴリズムを明らかにしています。 カットの下-詳細なデコードとスライド。
ほとんどのスライドは英語で作成されますが、同僚からすみません。 すべてを翻訳することは常に可能であるとは限らず、必ずしも必要というわけではありません。
このレポートは、ここで紹介した作品に基づいています。 最初の仕事-私は数学者です-私たちはジャーナルLaser Physics Lettersに招待されました。これは、対応するインデックスが1よりわずかに小さい数学的な高ランクのジャーナルとは異なり、3.2のインデックスを持っています。 すべてのHirschインデックスおよびその他が考慮されるようになったので、そのようなジャーナルで発行することが有用であることがわかりました-物理的。
最新の結果の1つは代数計算複雑性セミナーで発表されました。そのようなドイツのセンターがあります。 これらの結果を確認できます。 アーカイブは明確なものです。
モチベーションから始めましょう。 ダニエルは量子コンピューターがもうすぐ登場するだろうと冗談を言った。 カザンには、コンピューターを収集するグループと、ディレクターのDyachkov Viktor Vasilievichがいます。 彼はタンボフ出身で、とても元気です。 彼はどうやって私に会うのだろう、と彼は言う。「いつか量子コンピューターを売るのか？」
カナダ人はすでに売っています。 D-Waveコンピューターについて知っています。定期的にテストされ、カナダ人は最初の500キュビットであり、現在は1024キュビットであると発表しました。 テスト中に定期的に、これはすべてクラシックコンピューターで実行できることがわかりました。 しかし、これはまだこの状態です...
おそらく、個々のキュービット-および500、1024、およびそれ以上-を彫刻できると言えます。 しかし、実際には、量子コンピューターは、これらの量子ビットがもつれた、もつれた状態、つまりもつれた状態にある場合にのみ、非常に強力になります。 本質的に、これはキュービットがお互いを感じることができるようにシステムをプログラムできる状況です。 行うことはほとんど不可能です。
そのような量子レジスタを作成することが可能である場合-私は量子コンピューターについては話さない-連結状態が500のオーダーである場合、これは2,500の状態と同時に動作できるようなパフォーマンスを保証します。 これは宇宙の粒子の数であり、これは良いことです。 このシステムは、既存のすべてのコンピューターに勝ちます。
ここで言及されているShoreのアルゴリズムは、1994年の最初の結果です。 GoogleやYandexにQuantumアルゴリズム動物園とは何かを尋ねると、既存の古典的なアルゴリズムよりも1桁優れた50を超える量子アルゴリズムを含むページがすぐに展開されることを、多くの人が知っています。 潜在的に、量子マシン上で実行できるアルゴリズムのセットがすでに存在します。 そして最初のものは、ショアアルゴリズム、因数分解アルゴリズムです。 このビジネスのすべての哀れみは、Shoreアルゴリズムが登場したときに始まったばかりです。 因数分解とは、古典的なRSAアルゴリズムが量子コンピューターによって打ち負かされることを意味します。
これに対応して、このような傾向は、暗号化コミュニティですぐに現れました-量子暗号化後。 このような本がここにあります。 その中で、暗号コミュニティは、潜在的な量子コンピューターと戦うツールのセット全体を提案しました。
暗号学者はまた、そのような瞬間について話します-例えば、ランポートの署名システムなどのハッシュベースのデジタル署名準備スキームは、量子コンピューターにも負けません。
ランポートのデジタル署名とは何かを思い出します。 これはかなり単純なもので、1979年に提案されました。 レスリーランポートは、LaTeXの作成者として知られており、理論的および実用的なコンピューターサイエンスの分野で最も引用されている人物です。 彼は、LaTeXの作成者の1人であるという事実のため、非常に引用されています。
ランポートのデジタル署名は、ビット0と1に適切に署名できるシステムで、単語wは0に関連付けられ、別の単語vは1に関連付けられます。 これらは0と1の2つの秘密キーです。アリスは関数f（w）とf（v）の値を準備します。 一方向関数を取り、これらのペアをボブに転送する必要があると想定されています。 アリスが1に署名したい場合、元の単語vと1をボブに送信し、ボブはvからf（v）をすばやく計算し、これが真かどうかを確認します。
片側性は非常に大雑把に意味があります。 これは、関数の値によって引数を見つけるのが難しく、引数によって関数の値を計算するのが簡単であることを意味します。 それに基づいて、あなたは長いメッセージで同じことをすることができます...
私たちにとって有用な次のステップ：イプシロン万能ハッシュファミリーとは何かを思い出します。
N個のハッシュ関数のセットを取得します。 ハッシュ関数とは、長さKの単語を長さMの単語に圧縮する関数を意味します。K> M、ここでは競合が発生します-1つの単語に2つの異なる単語が表示される状況。 これは、K> Mのときに起こります。
そのようなハッシュ関数のセットを集めましょう。 以下が当てはまる場合、Fはイプシロンユニバーサルと呼ばれます。fがこのセットから等しく選択される状況では、2つの異なる単語が同じイメージを与える確率は小さくなります-イプシロン以下。 このようなファミリは、イプシロンユニバーサルハッシュファミリと呼ばれます。 そして、イプシロンが1 / Nの場合、これは普遍的なファミリーです。
epsilon-universal hashファミリのファミリを使用して、デジタル署名システムを配置できます。 これについては詳しく説明しません。 数学の部分について話し、それが実装されている場所とロシアでどのようなコミュニティが機能するかを説明します。
中心的なアイデア：ハッシュの概念と関数のハッシュファミリーを量子ケースに一般化します。 しかし、ポイントはこれです：単語を量子状態、量子ビット集合にマッピングします。 同時に、衝突がまれになるように、これら2つの要件を満たす必要があります。 つまり、意味のあることですが、引数の単語のわずかな変更でも、画像のハッシュが大幅に変更されるはずです。 そのため、クラシックでは必須です。 そしてもちろん、関数は一方向でなければなりません。
一方的な面に関しては、古典に飛びつきました。 一方向関数の概念は、大まかに言って、問題P≠NPと関連しています。 この条件が満たされている場合、一方向関数が存在します。それ以外の場合、潜在的に一方向関数を使用します。 そのような問題があります、私たちは皆それについて知っています。
ある意味で、最適なハッシュ関数を構築できる構造を提案します。 従来のエラー訂正コードを使用して、さまざまな量子ハッシュ関数のファミリ全体を構築できるようにする構成を提案します。 これは、ポスト量子暗号への貢献です。
Shoreアルゴリズムが古典と戦う場合、ここでの量子部分は、ある意味で将来の量子コンピューターとの闘争を強化することを可能にします。
ここでキュービットとは何かについて簡単に説明します。 量子ビットは、ベクトルa 0とa 1の座標が振幅の2乗の和が1に等しい複素数であるという性質を持つ、2次元ヒルベルト複素空間の単位ベクトルです。 実際、複素数は2次元です。 そして、正式に言えば、これは4次元のポイントです。 しかし、この比率は次元を1に減らし、その結果、キュービットは3次元空間のベクトルとして表すことができます。
さらに、これは、角度ψと角度Θの2つの自由度があることを意味します。 すべては極座標で行われます。 この成分は実振幅と呼ばれ、サインです。 そして、これはphase- eiφと呼ばれます。
a 0とa 1は、量子ビットを測定する場合、ゼロまたは1になる確率です。
ある意味で、キュービットの良い例えは、コインを取り、それを反転させ、飛行中に0と1になったときの状況です。それは落ちて、測定しました、古典的な確率的ビットは生きなくなり、0または1のように。あなたは2つのコインをドロップすることができますが、その後、それらは独立しています。 そして、量子ビットのシステムは、それらが連結されている場合、古典には類似性がないものです。
単一のキュービットで単語をエンコードするにはどうすればよいですか？ バイナリワードを数値として解釈します。 これは材料部分のみに関するものであり、位相部分はありません。 ψ（w）がそのような数であり、2 kを法とする数と見なす場合、単語は読み取った単語に応じた角度によって決定される単位ベクトルにエンコードされることは明らかです。 ここですべてが順調です。 これは、1つのキュービットで単語をエンコードする方法です。
したがって、物理的には、このようなエンコードは一方向の機能です。 アレクサンダー・セメノビッチ・ホレボの結果があります-彼はステクロフ研究所で働いています。 60年代後半に、彼は、量子ビット集団があれば、S量子ビットから抽出できる古典情報の最大値はSビットであることを示しました。 私は指で非常に有意義に話します。 この背後には明確な言葉があります。
そのため、1つのキュービットがあり、そこで単語を駆動した場合、長さKの単語から1ビットのみの古典情報を抽出できます。 これはまさに物理的な片面です。 ここでは、2つの単語が異なる状態でエンコードされています（そのような情報）。
ここで何が悪いのですか？ 2つの異なる単語は、近い状態にエンコードされる場合があり、見分けがつかないように見える場合があります。 1キュビットでは不十分です。
私が言ったことはすべて、フェーズの言語で書き直すことができます。 ここでは実際の振幅については説明しませんが、最初の部分、振幅0のベクトル、2番目の振幅1のベクトルを取り上げますが、ここでは位相を追加します。 フェーズを使用すると作業できますが、ここでは役に立たないでしょう。
これはどのように実装できますか？ このように1つのキュービットを構成するにはどうすればよいですか？ 実際、すべての変換はターンであり、単一です。 ゼロ状態から開始し、各ステップで次のビットを読み取ります...
R1、R2などは異なる必要があります。 角度は異なります。 ゆっくりと角を取り、結果として必要なものを手に入れます。
すでに優れた一方向の量子関数を持っているのに、Lamportの署名をどのように変換して量子化できますか？
前と同様に、単語wを選択し、それを0に関連付け、単語vを1に関連付けます。これらは0と1の秘密キーです。そして、公開キーを取得します。 これらはすでにwという単語に対応する量子状態です。1つの量子ビットにどのように入力できるかを示しました。 単語vも同じように入力されます。
0とそれに対応する量子状態1の値をBobに転送します。 Halevの結果により、プロセスを元に戻すことはできません。 次に、必要に応じて、ボブに2つの単語vと1を送信します。対応する状態と単語vを持つボブは、この単語を使用して量子状態ψ（v）が取得されたかどうかを確認できます。 ここで逆テストを提供します。
変換はユニタリ、つまり1対1であるため...単語wがあり、量子状態が準備され、ゼロから開始し、ユニタリ変換を適用し、必要な変換を蓄積します。 対応する条件が判明しました。 さて、単語wを取得すると、アルゴリズムを知っているボブはこの逆変換を整理できます。 簡単です。 そして、彼はこの変換を結果の量子状態に適用します。 その結果、2つの単語が同じ場合、結果は状態0になります。
比較する状態がわかります。 単語が等しい場合、逆検定とそれらが等しいという対応する確率は、次の式によって決まります。ベクトル0と受信した逆変換の状態のスカラー積。
2つの単語が同じ場合、それは常に1です。ここでは、間違えられません。 また、状態が等しくない場合、1つのキュービットのみを処理する場合でも、1つに近い状態を保つことができます。 これは、2つの状態、ψ（v）とψ（w）が近い場合です。
2つの異なる単語が状態をほぼ直交する状態に変換する状況を考え出す必要があります。 それは私たちにとって最適です。
次のステップは、1個のキュービットがなく、S個のキュービットのレジスタが必要な場合です。
1つのキュービットからこのようなシステムに移行できます。 これは、サイズ2のヒルベルト空間で作業し、対応するアンサンブルが1キュビットの場合と同じ方法で記述されることを意味します。 a iは振幅の複素数です。 このベクトルのノルムはまだ1です。これらの数値の2乗のノルムは、測定すると、基本状態iの1つになる可能性があります。
つまり、次のように配置された関数を検討すると言うことができます。長さKの単語は、S量子ビットの集合にマッピングされます。 レコードは次のようになります。
私はそれがどのように組織化されたかは言いません。これは、1量子ビットに対してどのように行われたかとの類推によって行うことができます。
結果は次のようになりました。 何を要求しますか？ 関数ψを呼び出します。この関数は、長さkの単語をS量子ビットの集合にマッピングします。直交。
この状況では、次の状態が発生します。 その後、検証のために、いわゆる逆テストの適用を開始した場合、2つの状態が同じであるというのは本当ですか？ 「はい」と言う可能性は、異なる単語のデルタ平方にすぎません。 単語が同じである場合、1の確率で「はい」と言います。これがまさに必要なことです。
定理は非常に簡単に証明されています。 そのようなδ-Resistant（|Σk |、s）-quantum関数を構築したい場合、sをlog（k）-log（log（1 +√（2/1 -δ ））より小さくすることはできません）-1。
下のマークがあります。 理論的な下限に近いこのような優れたデルタ安定量子関数を構築することは可能ですか？ 驚いたことに、それは判明-それは可能です。
将来を見据えて、長さkの単語が長さnの単語でエンコードされ、対応するフィールドF qで動作するように配置されたエラー訂正線形コードがある場合、事前に選択された任意のδに対してできるという結果を発表していますそして、ハミング距離nからこのコードdの特性に関連付けられているそのようなΔについて、コード長を構築します。 さらに、これに必要なキュービットの数はlog（n）以下です。
再びジャンプ-結果に気付き、非常に美しいリードソロモンコードでどのように見えるかを調べました。 そして、彼にとって次の特徴が得られたことが判明しました。 定数によるコードの長さが元のメッセージの長さよりも大きい場合、 k-1 / q +Θなどのエラーしきい値に対して 、特性log（q log（q））と何らかの種類のアドオンを使用して、対応する量子ハッシュコードを構築できます。 そして、このことは、ここにあるより低い推定値に十分近いです。
これは驚くべきことでした。 物理技術研究所でのセミナーでこれを語ったとき、アレクサンダー・セメノビッチ・ホレボは、下のマークを聞いて言った：もっともらしい、はい-しかし、構築する方法？ たとえば、リードソロモンコードを使用してこれを実行できるオプションについて彼と話し合ったとき、彼は何かがこの方向で実行できることに同意しました。
これは、ここに表示されるレポートの説明です。 次に、これについてもう少し詳しく説明します...
最初の例はこれでした。単語があり、それを1つの量子ビットにハッシュします。 ここで、s個のキュービットのアンサンブルを使用して、これらすべてをエンコードおよびハッシュする方法を決定する必要があります。 これはどのようなメカニズムですか？ この質問に答えるために、量子ハッシュジェネレータの概念を提案します。
最初の例。 いつものように、このようなものが世界にあったことが判明しましたが、別の言語で少し話されていました。 量子フィンガープリントや量子フィンガープリントなどがありました。 これは、アービターとの計算の特別な通信モデルのために2002年にHarry Boorman等によって行われました。 そして、これは量子ハッシュの特別なバイナリケースであることが判明しました。
コーディング理論の課題の1つは、バイナリコードからバイナリアルファベット以上に移行することです。 リードソロモンコードは基本的にバイナリではありません。ここでは、ゲームは高品質です。 2を超える別の特性のフィールドに移動すると、実際に前進します。
行われたことの最初の例を示します。 次に、エラー修正コードから移行してこの設計に投資する方法を示します。
イプシロンユニバーサルハッシュファミリがあります。 特定の関数ファミリーを使用して、1つの量子関数の生成を開始します。 古典的な線形関数のセットがあり、フィールドF qがあります。 それから係数を取り、関数H = {h 1 、...、h T }のセットを持っています。 ここで、h関数を使用して、この方法で1量子ビットの量子関数を生成します。 簡単にするために、フェーズではなく素材の振幅で作業します。 ある意味では、これは直感的に明らかです。ただし、物理学者は、フェーズの方が実装しやすいため、すべてをフェーズの言語に書き換えるように実装を求めています。
このような量子関数のセットを準備しています：| ψh j （w） ⟩= cos2πhj（w） / q |0⟩+ sin2πhj（w） / q |1⟩。
次に、これらの関数を次のように1つにまとめます。|ψH（w）⟩= 1 / √T
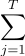|j⟩|ψh j （w）⟩。
重要なことは、このエントリは、これらすべてのT関数hの計算を同時に、等しく等しく確率的に開始することを意味します。 そして、この方法で計算を構築します-量子物理学はこれを可能にします。 私たちの前には、物理学が私たちにできることの数学的な記録があります。
レジスタjは、jのバイナリ表記として扱う必要があります。 もしそうなら、log（T）ビットがあれば十分です。キュービット状態はそれらに対応しています。 これがどのように行われるかについては詳しく説明しません。 また、log（T）キュービットは、最後のキュービットの計算をガイドします。 — . T — log(T) .
, , , . d, k n, , .
log(n) . — , E i (w). — , 90 . , 90 . log(n+1) , .
, , . , . - k, s s . .
. 2009 , , . , , . . , , , , 1993 . , , log(q) : T = ⎡( 2 / δ 2 ) ln(2q)⎤.
, log(k), -. -, q, log(k), s .
, : -. , G — - . - l , , , -, - , k d+l -, — -.
ó, 2008 .
-, -. , - -. .
— , . : - -, , N , k F q . : - — . , -, .
, F, . - . -, k s . Δ ≦ ε + δ — - - - - -, . - -.
. , - , .
, , computer science. , , 1979 , « fingerprinting», , . . , , p i . , p i .
« » 70-80- , , .
, , , - , 1/- , — . - -, , , , , , , fingerprinting - : -, k s . : — , 1/ — , — . . , .
-, , , , . , — -.
. - 1979-1980- — -. .
, , , . . . -, - . , — . , — , .
, . — log(k), — k. , , .
, . nkd, k n, F q , -. , -, , Δ = (1 – d/n) + δ. , , δ — , . s, , : s ≦ log(n) + log(log(q)) + 2*log(1/δ) + 4.
1994 , , , , , -. : - , , .
- 70-80- . , — , , : 50-60- . , 1994 . , , — . .
, - — , — -, -.
, . .
, . . , , -. , . - — , , . - — . .
. , .
. . , , , — .
? . , . , . , , . .
, , . . 100 , , . 100 , , . , — .
, , . — . ? , , . , , , , -.
, s 10, ? s 100? , , , . s 100 , -, — ?
, . . , … , . , . , .
, , . - . , . , , , — , . , . .
, . , , . « » . , , . . , . , . -84, -. 1984 , : .
, . , , , , , .
, . , .
, , , , , . .
おそらくそれだけです。 ありがとう
— ?
— . , -84 — , . , . -84 , . , , , — -.
. , . , — , . : , , - . . , . , . , -84, . , - .
— , , , , . ? , , .
— , . — . — , computer science. , , . , computer science — , , . . .
, , .
MIT. , , .
— . — . , . , , . , — , , — . , ! : . . — . , , .
, . , , — . , — - , . , . , .
? . : - , - principal investigator , . , . — , . . .
— . , Computer Science in Russia, . , scottaaronson.com/blog. , , . , . Quantum Computing since Democritus, « ». , .
-はい、先日、ニュースレターから、NPPOの完全な問題を迅速に解決しようとしている脳モジュールまたはその他のエンティティの出現について議論されているという情報を受け取りました。論争があり、アーロンソンが関与しています。見て、これは好奇心が強い。ところで、複雑な動物園を作成したのは彼でした-すべての複雑なクラスはどこにありますか。彼はバークレーの大学院生でしたが、彼らは彼からそれを買いました。よくできました。
ありがとう