 「Alt = "画像" />
「Alt = "画像" />
第3学年のBTFの証拠を提供することは適切だと思います。
まず、この手法によれば、どの程度でも同様に考えることができます。
第二に:初等数学に基づいた立方体の証拠はまだありません。
さらに、数値が小さいため、キューブを検討する際に計算が簡素化され、理解が容易になります。
証拠の実行に関する有益なコメントと、もちろん彼らの助けに対して、可能性のある相手に事前に感謝します。
そして少しの胆汁。 モスクワ州立大学のdxdy数学フォーラムでの証拠の認識には、本質的に理解の兆候はありません。
同時に、かなりの時間、専門的にもBTF問題を扱ってきた数学的コミュニティの一部が集中していることに注意する必要があります。 フォーラムで、dxdyは、キューブの検討に基づいて証明することを要求しました。 相互理解には役立ちませんでしたが、この要件は有用だと思います。 彼は尋ねた:「何が欠けているのか?他に何を考慮する必要があるのか?」 沈黙、またはせいぜい、長い間証明されてきたことを証明するための推奨事項であり、間違いなく相手は知っています。 現在、このトピックはdxdyフォーラムで取り上げられています。読むことはできますが、フィードバックはありません。 多分Habrhabrの誰かが要件を指定しています。 意見を聞きたいです。
条件を満たしている場合、証明は公平と見なすことができます。
指数nは素数です。 [1]
キューブのフェルマーの大定理の証明を考えてみましょう。
それを証明する必要があります

整数あり
 不可能。
不可能。
エントリー
1.1既存の伝統によると、証明は学位の違いを考慮します

根拠の選択の利便性に基づいて:

そして
 。
。
1.2この場合、学位を考慮すると、フェルマーの大定理(BTF)の間で2つのケースが区別されます。
1.1 BTFの最初のケースには、BTFの2ケースを提供するベースを除き、任意のベースとの正確な程度の違いが含まれます。
1.3最初の場合には、次のものがあります。
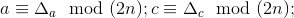

互いに素な数であり、底
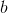 -でも。
-でも。
すなわち、このオプションによれば、証拠を見つけることが必要であり、まずBTFの2番目のケースについてです。
1.4 BTFの最初のケースの平等1.1の根拠を共通の議論の観点から表現し、そのために以下の表記法を導入します。
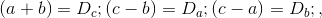
たとえば
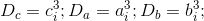
どこで
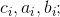 整数です。 [2]
整数です。 [2]
1.5したがって、等式1.1は次のように表すことができます。
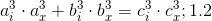
または
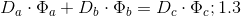
ここで:

2.1 BTFの最初のケースとBTFの2番目のケースは両方とも、学位とその基盤の通約可能性に基づいて証明されています。
 。
。
証明は、数量の比較に基づいています。
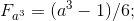 -度計と
-度計と
 -ベースメーター付き。
-ベースメーター付き。
2.2を使用してBTFの最初のケースを証明するとき
 残基クラス1および5、根拠を表現できます
残基クラス1および5、根拠を表現できます
 :
:
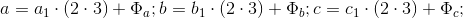
ここで:
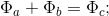
同時に
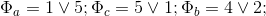
2.3 BTFの最初のケースを検討する場合、
 拠点
拠点
 控除の最初または5番目のクラスに属する場合があり、
控除の最初または5番目のクラスに属する場合があり、
 -それどころか。
-それどころか。
なぜなら、偶数クラスの残基に属する塩基は、3番目のクラスの残基に属する塩基と同様に適切ではないためです。なぜなら、この場合、共通因子がすべての塩基に現れ、定理の条件に反するからです。
2.4特定のクラスの残基に属する次数の基底を考慮する場合、フェルマー方程式の基底の値の修正は、

BTFの最初と2番目のケースの特徴は、設計パターンに影響しますが、提案された証拠にとって基本的な重要性はありません。
3.1 BTFの2番目のケースの証拠を検討する場合、根拠の控除のクラスの選択

そして

問題の学位の指数を使用して相互に単純な控除のクラスを転送する可能性に基づいて、正確な程度に等しい係数を使用して、根拠の最初のクラスへの変換を常に使用できるため、それは重要ではありません。 (フェルマーの小定理)。
したがって、BTFの2番目のケースを検討する場合、次の場合にオプションを検討するだけで十分です。

3.2 BTFの2番目のケースでは、より詳細に検討されます。
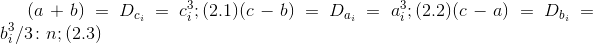
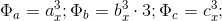
そして
 どこで
どこで

自然数系列の正の数で、大きさは互いに素です。
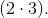
BTFの2番目のケースの証明。
4.1既存のパターン:
価値
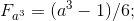
正確なキューブには、必ず要因が含まれます

そして要因
 。
。
したがって、量を考慮する機会が得られます
 。
。
4.2見つかったパターンに基づいて、次の質問に答えるために次数差の分析に進みます。
数量
 因子を含む場合があります
因子を含む場合があります
 ?
?
4.3提起された質問に答えるために、度の差を

根拠の提示に基づいて

そして

を通して

そして
 ニュートンのビノムの使用。 [3]
ニュートンのビノムの使用。 [3]
5.1度の差をある値にする可能性
 使用により提供
使用により提供
 。
。

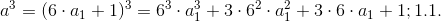 。
。
5.2違いを決定します(1.1.s-1.1.a):
![(c ^ 3-a ^ 3)= 6 ^ 3 \ cdot [(c_1)^ 3-(a_1)^ 3] +3 \ cdot 6 ^ 2 \ cdot [(c_1)^ 2-(a_1)^ 2] +3 \ cdot 6 \ cdot [(c_1)-(a_1)]; 1.1](https://habrastorage.org/getpro/habr/post_images/2e9/e39/28a/2e9e3928a25f05e2b3c7ed9e0276fca6.gif) 。
。
5.3定義
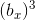 。
。
![(c ^ 3-a ^ 3)/ [3 \ cdot 6 \ cdot(c_1-a_1)] = 6 \ cdot 2 \ cdot [(c_1)^ 2 + c_1 \ cdot(a_1)+(a_1)^ 2] + 6 \ cdot [(c_1)+(a_1)] + 1 = b_x ^ 3; 1.1.k](https://habrastorage.org/getpro/habr/post_images/83f/241/a0a/83f241a0aa25fdfd5b3ff68b80033d6d.gif)
5.4定義

![F_ {b_ {x} ^ {3}} =(b_ {x} ^ {3} -1)/ 6 = 2 \ cdot [(c_ {1})^ {2} + c_ {1} \ cdot a_ { 1} + a_ {1})^ {2}] + [(c_ {1})+(a_ {1})]; 1.1.k.1](https://habrastorage.org/getpro/habr/post_images/223/2ae/eff/2232aeeff09f111afbbbf7fcc022bc79.gif)
2つの項の合計を取得します。最初の項には因子が含まれています
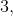 2番目はそうではありません。
2番目はそうではありません。
5.5これは、
![[(c_1)+(a_1)];](https://habrastorage.org/getpro/habr/post_images/e06/f46/80d/e06f4680d55a59544ff8cadd7de25e98.gif) 要因
要因 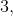 含まれていませんが、違い
含まれていませんが、違い

少なくとも1つの要素を含む
 。
。
この場合、数量
 含む因子
含む因子
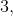 できません。
できません。
このオプションでは、すべてが明確です。
5.6次数差の正確な立方体を確保するために、因子の不在

サイズで

私たちは、BTFに反論することは不可能であると考えています。
6.1共通の要因が存在する場合の理由の質問に答えるため
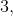 大量に
大量に
 そして
そして

立方体の違いで正確な立方体を取得することは不可能であるため、量の形式化された表現を使用します。

6.2形式的な表現
 ;
;
 O.1
O.1
計算例A:

 ;
;
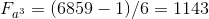 ;
;
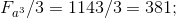
6.3定義

を通して


6.4一般的に:
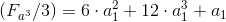 ; D.1
; D.1
6.5正確なキューブはどこから来たのか:
 。
。
このパターンは、係数を計算できるように照らされています

サイズで
 。
。
7.1ここで、数量にどのような値が提供されるかを自問します

因子メンテナンス
 、
、
正確な立方体を考慮する場合、同様の値の充填に対応する量で。
例:
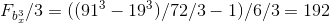 。
。
以来

疑惑度の根拠は
 、
、
マイナス1には2つの要因が含まれます
 。
。
7.2以降
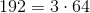 、
、
この仮定の下で

単一の因子を含む
 、
、
必要な量の充填が提供されます

補因子
 。
。
7.3この結果が得られる理由の質問に答えてみましょう。
グレードベースの選択

そして

条件が満たされていることを確認しました。

そして

共通の要素を1つ含む
 。
。
7.4これを達成しました。
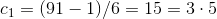
そして

しかし、大きさを分析する
 、
、
単一の要因ではないことに注意してください
 、
、
でも

この結果は、合計
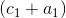
計画外の追加要因が含まれています
 。
。
7.5この要因は、私たちの意見では、原因不明とみなすことができます。
無限小との類似性を引き出すと、最終結果に無限小が影響を与えないのとは対照的に、考慮されていない因子が、想定された真度に存在する法則の同一性を保証し、検討中の問題を生成した不確実性を提供することがわかります。
私たちの意見では、原因不明の要因の発見は、BTFの証拠を見つけることが困難である理由の説明を提供します。
8.1さらに、学位のベースの違いを決定する際に考慮されない要因の存在に注意することができます

そして

度の差で正確な立方体を取得する可能性、および値に原因不明の要因が発生する可能性を除外します

予測可能な結果を提供するパターンです。
8.2そして、私たちの意見では、これは、3次のフェルマー方程式を検討するとき、および共通の要因の存在下でなぜの質問に答えるとき、2番目のケースのBTFステートメントに反論する障害です
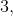
大量に

そして

BTFの反論は不可能です。
8.3私たちには平等を書く権利があります。
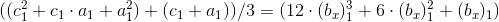 、
、
または
 。
。
8.4次のように書くことができます:
 。 T
。 T
8.5状態を考慮してください:
 。
。
この状態の場合
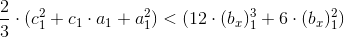
より大幅に
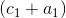 。
。
8.6これは、

意味がありません。
8.7 BTFの反論の不可能性をより低い値で示す
 、
、
私たちは、量の法則を考慮する例で、そのようなイベントの可能性の考慮に移ります

そして、以下を掛けて正確な立方体を得ることに対応する同じ量
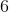
および追加
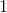 。
。
8.8これらの値の比率を考慮する理由。
で
 、
、
でも

同時に、同じ値を取得することも考慮されます。
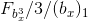
理由のために

そして
 、
、
パターンを確認します。
8.9キューブのベースを
 、
、
数値の一連の値を作成できます
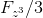 、
、
整数値の場合
 :
:

そして
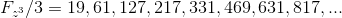 。
。
計算値を取得する
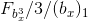 、
、
それらを可能な値と比較する機会を得る
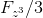 。
。
8.9.1
1. a
1。
 。
。
2。
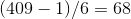 。
。
3。
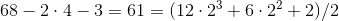 。
。
1.c
1。
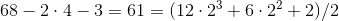 。
。
2。
 。
。
3。
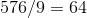 。
。
4。
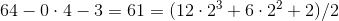 。
。
8.9.2
2. a
1
 。
。
2。
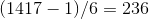
3。
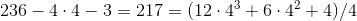
2.c
1。

2。
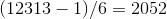
3。
 。
。
4。
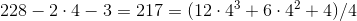 。
。
8.9.3
3. a
1
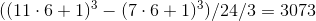 。
。
2。
 。
。
3。
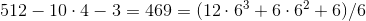 。
。
3.c
1。
 。
。
2
 。
。
3。
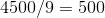 。
。
4。
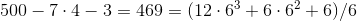 。
。
8.10
キューブの違いに対する比較値の計算を検討し、BTFの反論の可能性についての仮定を提供します。
ベース間の範囲は
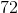 。
。
8.10.1の場合
 、
、

私たちは得る
 、
、
どこで
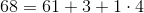
のために
 、
、
で
 。
。
基底の違いに興味があるので
 、
、
でも
 、
、
これらの値を使用して同様の計算を実行します。
 。
。
値を比較する

そして
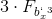 。
。
 。
。
どこで:
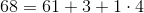 、
、
のために
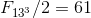 。
。
8.10.2同様に、

そして

 。
。
どこで
 、
、
のために
 。
。
8.10.3同様に、

そして
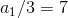
 。
。
どこで
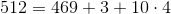 、
、
のために
 。
。
8.10.4同様に、
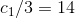
そして

 。
。
どこで
 、
、
のために
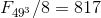 。
。
比較する量の差の減少に影響する形式化された値を取得しますが、部分的にはマイナス記号付きの追加増分として取得します。
8.11数値シリーズに基づく
 :
:
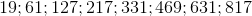 、
、
隣接する値の間の差は、直接比較する量の差よりも常に大きいことがわかりました。したがって、値が3倍になったときです。
8.12計算に基づいて、次のパターンが表示されます。
1.得られた値の間の最小範囲
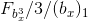
そしてその真の意味

厳密な規則性に基づいて増加しますが、これは形式化できます。
同時に、一連の数値のいずれかと比較して、数値的に増加し、最小のままです。
 、
、
つまり、いつ

そして最大

2.したがって、量は

本当に可能なそのような量に同じ依存関係にあります。
これにより、BTFの2番目のケースに対するBTFの反論はキューブでは不可能であると主張する権利が与えられます。
9.000むかしむかし、dxdyフォーラムで、誰かが、私の意見では、Brokvalubのログインで、私に書いた:
「フェルマーの大定理を本当に扱いたいですか?」
そして、そのように降りてみませんか。
このアプローチでは、質問が未回答のままになることはありません。
他に何が必要ですか?
もちろん、もちろん、明確なプレゼンテーションと認識。
誰かがHabrahabrに、証拠はその認識後にのみ証拠になると書いた。
なりませんが、考慮されます。
そして、トリッキーな質問が残っていない場合に証拠になります。
そのような質問は現時点では私には知られていない。
本当の、静かな相手と。
対談者、できれば共著者がいる場合、何かを検討することができます。 以下に詳細を説明します。
それでも、ショーは証明よりも困難でした。
9.1ここで、キューブのBTFの最初のケースの機能について考えてみましょう。
この目的のために、見つかったもう1つの規則性を考慮します。
決定する際に
 公平:
公平:
![F_ {b_x ^ n} =(b_x ^ n-1)/(2n)= [(c ^ na ^ n)/ [n(ca)]-1] /(2n)$$ = [[((c ^ n -1)/(2 \ cdot n)-(a ^ n-1)/(2 \ cdot n)] / [n \ cdot(c_1-a_1)] -1] /(2 \ cdot 3); F_ {b_x ^ n} =(b_x ^ n-1)/(2n)= \ frac {[(c ^ na ^ n)/(ca)-1]} {2n} = \ frac {[(c ^ n \ pm \ Delta_c)/(2n)-(a ^ n \ pm \ Delta_a)] /(2n)-(c_1-a_1)} {ca};](https://habrastorage.org/getpro/habr/post_images/da0/826/0d1/da08260d182e2fd35ade19371cd46c0b.gif)
9.2 A、正確に。
![F_ {b_x ^ n} =(b_x ^ n-1)/(2n)= \ frac {[(c ^ na ^ n)/(ca)-1]} {2n} = \ frac {[(c ^ n \ pm \ Delta_c)/(2n)-(a ^ n \ pm \ Delta_a)] /(2n)-(c_1-a_1)} {ca} w](https://habrastorage.org/getpro/habr/post_images/790/a27/cdb/790a27cdb8b9f53f6ff59166405de8f6.gif) 。
。
調整の必要性

数量の違いによる
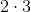 計算に受け入れられました。
計算に受け入れられました。
9.3これにより、BTFの最初のケースの次数の違いを見つけると、BTFの2番目のケースと同じ類似のバリアントが得られるため、2番目と1番目のケースの考慮を同等にすることができます。
したがって、フェルマーの大定理の記述は、立方体を検討するときの2番目のケースと1番目のケースの両方で有効であることに注意できます。
証明するために必要でした。
PS任意の次数の証明は、数値形式と、もちろん形式化された形式の両方の計算機能により、立方体の証明とは異なります。
さらに、量の形式化
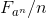
キューブを検討する際に使用される同様の誤計算に基づいています。
検討中の度合いが増加するBTFを考慮する場合の未考慮の要因の発生は、キューブを検討する場合のそのような要因の発生の説明と同様の説明を持っています。
上記に加えて、任意の指数のBTF証明は、キューブの検討で見つかった基礎の使用を通じても見られることに注意する必要があります。
もちろん、特別に考慮されていないすべてのことは特別に考慮する必要がありますが、それだけでは著者の責任ではありません。
残念ながら、Habrahabrでは、希望は提供されません。
しかし、希望はこれが誰かに役立つかもしれないということです。
著者は、証拠の真実を疑わず、これに満足しています。
そして、特に、その基礎的な性質にもかかわらず、その由緒ある兄弟が常に成功するとは限らないという点に到達することを可能にする法律、いわゆる初等数学の使用によって証明が可能になったという事実。
短くして磨く証拠があります。
そして、ここでは、アドバイスは害になりません。
ただし、抗議者がいる場合、または棄権した場合は、試合へようこそ。
参照:
1. G.エドワーズ「フェルマーの最後の定理」
2. M.M. ポストニコフ「代数的数論の紹介」
3.M.Ya。 Vygodsky「初等数学のハンドブック。」