統計は、たとえば、決定論的モデルを構築する方法がない場合、要因が多すぎる場合、または利用可能なデータを考慮して構築されたモデルの尤度を評価する必要がある場合など、多くの問題の解決に役立ちます。 統計に対する態度はあいまいです。 嘘、露骨な嘘、統計の3種類の嘘があると信じられています。 一方、統計の多くの「ユーザー」は彼女を信頼しすぎており、その仕組みを完全には理解していません。たとえば、正規性を確認せずにデータに学生のテストを適用します。 このような過失は深刻な間違いにつながり、 学生のテストの 「ファン」を統計の嫌悪に変える可能性があります。 iの上にドットを置いて、特定の現象とそれらの間に存在する遺伝的関係を記述するために使用するランダム変数のモデルを見つけてみましょう。
まず第一に、この資料は確率論と統計学を勉強している学生にとって興味深いものになりますが、「成熟した」専門家はそれを参考として使用することができます。 次の作業の1つでは、統計を使用して、為替取引戦略の指標の重要性を評価するためのテストを構築する例を示します。
離散分布は作業で考慮されます。
連続分布と同様に：
記事の最後に、思考に関する質問が出されます。 このテーマに関する私の考えを次の記事で紹介します。
与えられた連続分布のいくつかは、 ピアソン分布の特定のケースです。
離散分布
離散分布は、孤立点で定義された区別できない特性を持つイベントを記述するために使用されます。 簡単に言えば、成功または失敗、整数（ルーレット、サイコロなど）、イーグル、またはテールなど、いくつかの個別のカテゴリに結果を帰することができるイベントの場合です。
イベントの可能な結果のそれぞれの発生確率の離散分布が記述されています。 離散イベントの分布（連続を含む）については、期待値と分散の概念が定義されています。 ただし、一般的な場合、個別のランダムイベントの期待値は、単一のランダムイベントの結果として実現できるのではなく、イベントの結果の算術平均がその数が増加するにつれて増加する値として実現可能であることを理解する必要があります。
イベントの結果の確率は、組み合わせの総数に対する望ましい結果を与える組み合わせの数の比率として定義できるため、離散ランダムイベントのモデリングでは、組み合わせ論が重要な役割を果たします。 例：3個の白いボールと7個の黒いボールがバスケットに入っています。 バスケットから1つのボールを選択すると、10通りの方法（組み合わせの合計数）で行うことができますが、白いボールが選択されるのは3つのオプションのみです（3つの組み合わせで目的の結果が得られます）。 したがって、白いボールを選択する確率：
（ ベルヌーイ分布 ）。
戻りのあるサンプルとないサンプルも区別する必要があります。 たとえば、2つの白いボールを選択する確率を説明するには、最初のボールをバスケットに戻すかどうかを決定することが重要です。 そうでない場合は、戻り値のないサンプル（ 超幾何分布 ）を扱っており、確率は次のようになります。
-最初のサンプルから白いボールを選択する確率に、バスケットに残っているボールから再び白いボールを選択する確率を掛けます。 最初のボールがバスケットに戻された場合、これは戻りのある選択（ 二項分布 ）です。 この場合、2つの白いボールを選択する確率は 
。
二階
ベルヌーイ分布
（ ここから取られます ）
バスケットの例を次のように形式化する場合：イベントの結果を、確率を持つ2つの値0または1のいずれかにしましょう
そして 
したがって、提案された各結果の確率分布は、ベルヌーイ分布と呼ばれます。
確立された伝統によれば、値が1の結果は「成功」と呼ばれ、値が0の結果は「失敗」と呼ばれます。 明らかに、「成功または失敗」の結果を得るには確率が伴います
。
ベルヌーイ分布の期待値と分散：
二階
二項分布
（ ここから取られます ）
数量
の成功 
結果はベルヌーイによって成功の確率で配布されます （バスケットにボールを返す例）、二項分布によって記述されます：
どこで
-の組み合わせの数 によって 。
別の方法では、二項分布は
成功の確率を持つベルヌーイ分布が可能な独立したランダム変数 。
期待と分散：
二項分布は、リターンのあるサンプル、つまり一連のテスト全体で成功の確率が一定のままであるサンプルに対してのみ有効です。
数量
そして 
パラメータを持つ二項分布を持っている 
そして 
したがって、それらの合計もパラメータとともに二項分布します 
。
二階
幾何分布
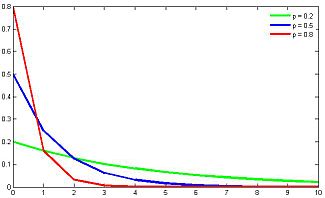
（ ここから取られます ）
バスケットからボールを引き出し、白いボールが引かれるまでボールを戻す状況を想像してください。 そのような操作の数は、幾何分布によって記述されます。 つまり、幾何分布はテストの数を表します
各テストで成功する確率を持つ最初の成功まで 。 もし テスト番号が成功した場合、幾何分布は次の式で記述されます。
幾何分布の期待値と分散：
幾何学的分布は遺伝的に指数分布に関連しています。 指数分布は、連続するランダム変数を表します。イベントの前の時間で、イベントの強度は一定です。 幾何分布も負の二項分布の特殊なケースです。
二階
パスカル分布（負の二項分布）
（ ここから取られます ）
パスカル分布は、 幾何学的分布の一般化です。故障数の分布を記述します
独立した試験で、その結果はベルヌーイに従って成功の確率で分配されます 発症前 
合計で成功。 で 
、数量の幾何分布を取得します 
。
どこで
-の組み合わせの数 によって 。
負の二項分布の期待値と分散：
Pascalに分布する独立したランダム変数の合計もPascalに分布します。
分布がある 
、そして - 
。 みましょう そして 独立した場合、それらの合計には分布があります 
二階
超幾何分布
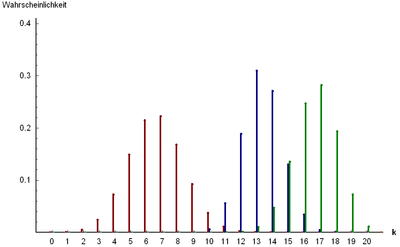
（ ここから取られます ）
これまで、リターンサンプルの例を見てきました。つまり、結果の確率は試行ごとに変化していません。
次に、返品せずに状況を検討し、所定数の成功と失敗（バスケット内の所定数の白と黒のボール、デッキ内の切り札、バッチ内の欠陥部品など）でセットから成功したサンプルの数の確率を説明します。
総人口に含まれる
そのオブジェクト 
「1」としてマークされ、 
「0」など。 ラベル「1」のオブジェクトの選択を成功と見なし、ラベル「0」のオブジェクトの選択を失敗と見なします。 n個のテストを実行し、選択したオブジェクトはそれ以上のテストに参加しなくなります。 発生確率 成功は超幾何分布の影響を受けます。
どこで
-の組み合わせの数 によって 。
期待と分散：
二階
ポアソン分布
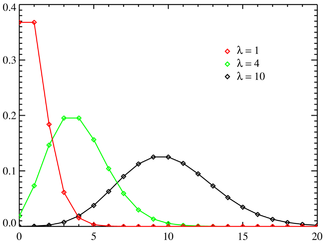
（ ここから取られます ）
ポアソン分布は、その「対象」領域で上記で検討した分布とは大きく異なります。現在、検討されるのは特定のテスト結果の発生確率ではなく、イベントの強度、つまり単位時間あたりのイベントの平均数です。
ポアソン分布は、発生確率を表します
長期にわたる独立したイベント 
イベントの平均強度で 
：
ポアソン分布の期待値と分散：
ポアソン分布の分散と期待値は同じです。
ポアソン分布は 、独立したイベントの発生間の時間間隔を表す指数分布と組み合わせて、信頼性理論の数学的基礎を形成します。
二階
連続分布
連続分布は、離散分布とは対照的に、確率密度（分布）関数によって記述されます
特定の間隔で一般的な場合に定義されます。
量の確率密度がわかっている場合
： 変換が定義されています 
、yの確率密度は自動的に取得できます。
一意性と差別化の対象
。
確率密度
確率変数の合計 そして 
（ 
）ディストリビューションあり そして 
畳み込みで記述 
そして 
：
ランダム変数の合計の分布が項と同じ分布に属する場合、そのような分布は無限割り切れと呼ばれます。 無限に割り切れる分布の例： 正規分布、 カイ二乗 分布 、 ガンマ 分布 、 コーシー分布 。
確率密度
ランダム変数xとyの積（ 
）ディストリビューションあり そして 次のように計算できます。
以下の分布のいくつかは、ピアソン分布の特定のケースです。これは、方程式の解です：
どこで
そして 
-分布パラメーター。 パラメーター値に応じて、12種類のピアソン分布が知られています。
このセクションで説明する分布は、互いに密接に関連しています。 これらの関係は、一部の分布が他の分布の特定のケースであるという事実で表現されているか、他の分布を持つランダム変数の変換を記述しています。
次の図は、このホワイトペーパーで検討する連続分布のいくつかの関係を示しています。 図では、実線の矢印はランダム変数の変換を示し（矢印の先頭は初期分布を示し、矢印の末尾は結果の分布を示します）、点線は一般化関係を示します（矢印の先頭は分布を示します。これは、矢印の末尾で示される分布の特殊なケースです）。 破線矢印の上のピアソン分布の特別な場合には、対応するタイプのピアソン分布が示されます。
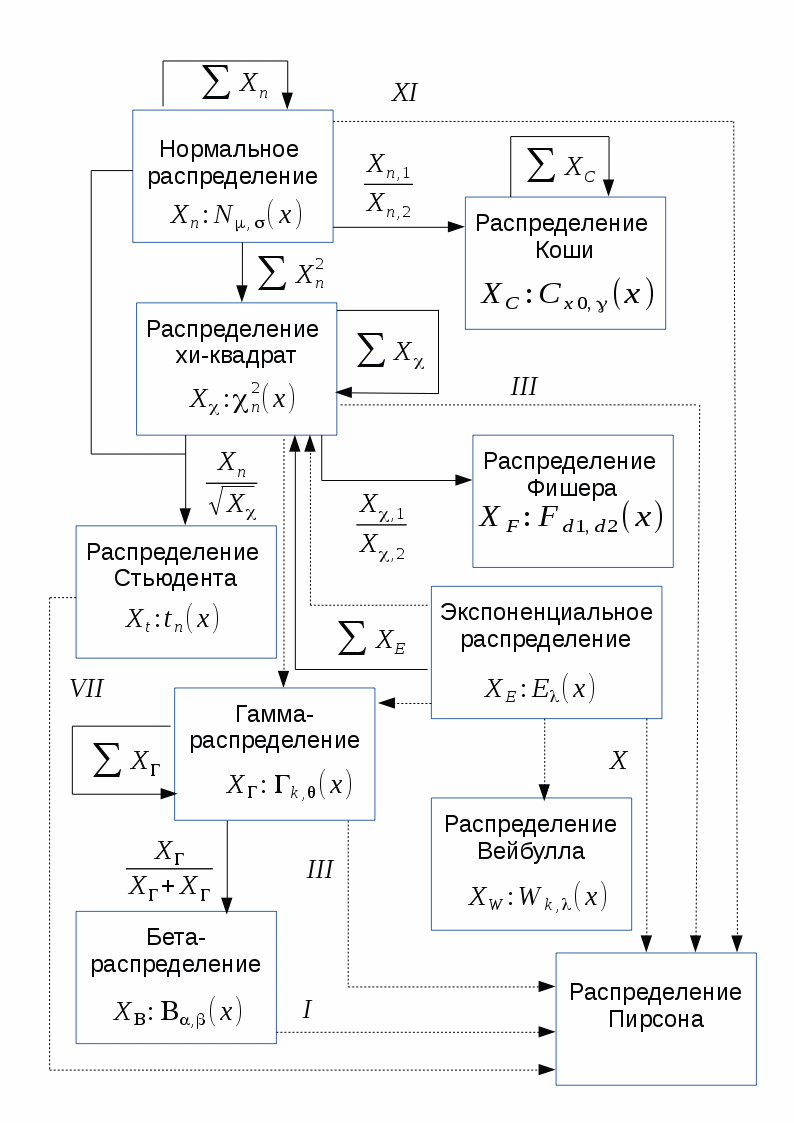
以下に提案する分布の概要は、データ分析とプロセスモデリングで遭遇する多くのケースをカバーしていますが、もちろん、科学に知られているすべての分布が含まれているわけではありません。
二階
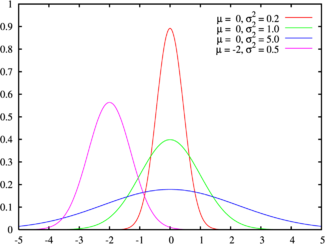
正規分布（ガウス分布）
（ ここから取られます ）
正規分布の確率密度
パラメータ付き 
そして 
ガウス関数によって記述されます：
もし
そして 
、そのような分布は標準と呼ばれます。
正規分布の期待値と分散：
正規分布のドメインは実数のセットです。
正規分布は、 ピアソンタイプXI分布です。
独立正規値の二乗和はカイ二乗分布を持ち、独立ガウス値の比率はコーシー分布です。
正規分布は無限に割り切れます：正規分布量の合計
そして パラメータ付き 
そして 
したがって、パラメータを持つ正規分布もあります 
どこで 
そして 
。
正規分布は、自然現象、熱力学的ノイズ、測定誤差を表す量をうまくモデル化します。
さらに、中心極限定理によれば、同じ次数の多数の独立項の合計は、項の分布に関係なく正規分布に収束します。 この特性により、統計分析では正規分布が一般的であり、多くの統計テストは正規分布データ用に設計されています。
z検定は、正規分布の無限の可分性に基づいています。 このテストは、正規分布数量のサンプルの期待値が特定の値に等しいことを確認するために使用されます。 分散の値はわかっている必要があります 。 分散値が不明で、分析されたサンプルに基づいて計算される場合、学生分布に基づいたt検定が適用されます。
n個の独立した正規分布量のサンプルを見てみましょう
標準偏差の母集団から という仮説を立てる 
。 それから量 
標準正規分布になります。 得られたz値を標準分布の分位数と比較すると、必要な有意水準の仮説を受け入れるか拒否することができます。
ガウス分布が広く分布しているため、統計をあまり知らない多くの研究者は、正規分布のデータを確認したり、分布密度のグラフを「目で」評価したり、盲目的にガウスデータを扱っていると考えています。 したがって、正規分布用に設計されたテストを大胆に適用し、完全に誤った結果を取得します。 おそらく、ここから統計に関するうわさが最も恐ろしい嘘になったのでしょう。
例を考えてみましょう。特定の値の抵抗のセットの抵抗を測定する必要があります。 抵抗は本質的に物理的であり、公称値からの抵抗の偏差の分布は正常であると仮定するのが論理的です。 測定し、抵抗の公称値付近のモードで測定値の確率密度のベル型関数を取得します。 これは正規分布ですか？ その場合、事前に分布の分散がわかっている場合は、 スチューデント検定またはz 検定を使用して欠陥のある抵抗器を探します。 多くの人がそうするだろうと思います。
しかし、抵抗測定技術を詳しく見てみましょう。抵抗とは、流れる電圧に対する印加電圧の比として定義されます。 デバイスで電流と電圧を測定しましたが、デバイスには通常、分布誤差があります。 つまり、電流と電圧の測定値は、測定値の真の値に対応する期待値を持つ正規分布乱数値です。 そして、これは、得られた抵抗値がガウスではなくコーシーに従って分布することを意味します。
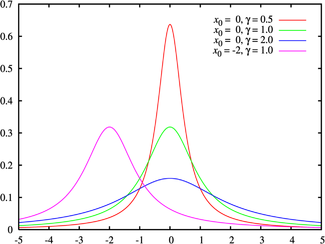
コーシー分布は、外向きの正規分布に似ていますが、裾が大きくなっています。 したがって、提案されたテストは不適切です。 コーシー分布に基づいてテストを作成するか、抵抗の2乗を計算する必要があります。この場合、パラメーター（1、1）を持つフィッシャー分布になります。
スキームに
二階
カイ二乗分布
（ ここから取られます ）
配布
量を説明する 確率変数の二乗 それぞれ標準標準法に従って配布されます 
：
どこで
-自由度の数、 
。
期待と分散分布
：
スコープは、負でない正の整数のセットです。
は無限に割り切れる分布です。 もし そして -配布者 そして持っている 
そして 
それぞれ自由度、そしてそれらの合計もまた分配されます そして持っている 
自由度。
は、 ガンマ分布の特別な場合（したがって、 ピアソンタイプIII分布）であり、 指数分布の一般化です。 分配された量の比率 フィッシャーによって配布された。
配布中
ピアソンの同意基準に基づいています。 この基準を使用すると、特定の理論的分布に対する確率変数のサンプルの妥当性を検証できます。
いくつかのランダム変数のサンプルがあるとします
。 このサンプルに基づいて、確率を計算します 
ヒット値 で 間隔（ 
） また、分布の分析的表現についての仮定があり、それに応じて、選択された間隔に入る確率は 
。 それから量 
通常の法律に従って配布されます。
あげる
標準正規分布に： 
、
どこで
そして 
。
得られた値
パラメーター（0、1）を持つ正規分布を持ち、したがって、それらの平方和は と 
自由度。 自由度の低下は、区間に入る確率の合計に対する追加の制限に関連付けられています。1に等しくなければなりません。
価値の比較
分布変位値あり 目的の有意水準のデータの理論的分布の仮説を受け入れるか拒否することができます。
スキームに
二階
学生分布（t分布）
（ ここから取られます ）
学生分布は、t検定を行うために使用されます： 標準正規分布ランダム変数のサンプルの特定の値への期待値の同等性、または同じ分散を持つ2つの正規サンプルの期待値の同等性のテスト （分散の同等性はf-testでチェックする必要があります）。 スチューデントの分布は、 カイ2乗に分布する値に対する正規分布確率変数の比率を表します。
T検定は、標本の分散または標準偏差が不明であり、標本自体に基づいて推定する必要がある場合のz検定に類似しています。
通常のサンプルの期待値が特定の値に等しいかどうかをチェックする例を考えてみましょう。サンプルを与えてみましょう
ある一般的な母集団からの通常の量のボリュームnを提案し、この母集団の期待値が 
。
値を計算する
。 この値はカイ二乗分布になります。 それから量 
学生に配布されます 
c 自由度、ここで：
どこで
-オイラーのガンマ関数。
得られた値をスチューデント分布の分位数と比較し、平均値と値の等値性の仮説を受け入れるか拒否することができます
必要なレベルの重要性を持つ。
学生分布の期待値と分散：
で
。
スキームに
二階
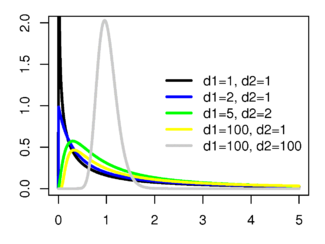
フィッシャー分布
（ ここから取られます ）
させる
そして 自由度を持つカイ二乗分布を持つ独立したランダム変数 そして それに応じて。 それから量 
自由度のあるフィッシャー分布を持つ 
、および値 
-自由度を持つフィッシャー分布 
。
フィッシャー分布は、実数の非負の引数に対して定義され、確率密度があります。
フィッシャー分布の期待値と分散：
期待は
および分散 
。
回帰パラメーターの有意性の評価、不均一分散性検定、 正常標本の分散の等価性の検定など、多くの統計検定はフィッシャー分布に基づいています（f検定、フィッシャーの正確検定とは区別されるべきです）。
F検定：2つの独立したサンプルがあります
そして 
正規分散ボリューム そして それに応じて。 サンプルの分散の等価性に関する仮説を提示し、統計的に検証しましょう。
値を計算する
。 彼女は自由度を持つフィッシャー分布を持つことになります 
。
価値の比較
対応するフィッシャー分布の分位数を使用して、サンプルの分散が目的の有意水準と等しいという仮説を受け入れるか拒否することができます。
スキームに
二階
コーシー分布
（ ここから取られます ）
コーシー分布は、2つの正規分布確率変数の比率を表します。 他の分布とは異なり、Cauchy分布の期待値と分散は定義されていません。 せん断係数は、分布を記述するために使用されます。
そしてスケール 
。
コーシー分布は無限に割り切れます。コーシーに分布する独立したランダム変数の合計もコーシーに分布します。
スキームに
二階
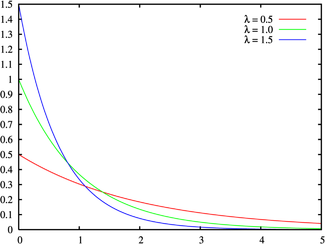
指数（指数）分布とラプラス分布（二重指数、二重指数）
（ ここから取られます ）
指数分布は、中程度の強度で発生する独立したイベント間の時間間隔を表します
。 特定の期間にわたるこのようなイベントの発生数は、離散ポアソン分布によって記述されます。 指数分布とポアソン分布は、信頼性理論の数学的基礎を形成します。
信頼性の理論に加えて、指数分布は、事象の流れをシミュレートする必要があるあらゆる場所で、社会現象の説明、経済学、大規模サービスの理論、輸送物流で使用されます。
指数分布はカイ二乗分布 （n = 2の場合）の特殊なケースであり、したがってガンマ分布です。 指数分布量は2自由度のカイ2乗であるため、2つの独立した正規分布量の平方和として解釈できます。
さらに、指数分布はワイブル分布の正直なケースです。
指数分布の離散バージョンは幾何分布です。
指数分布の確率密度：
非負の実数値に対して定義
。
指数分布の期待値と分散：
指数分布の確率密度関数が負の値の領域にミラーリングされている場合、つまり
に 
次に、二重指数または二重指数とも呼ばれるラプラス分布を取得します。
（ ここから取られます ）
より一般化するために、横軸に沿って分布の左右の部分の「接続」の中心をシフトするシフトパラメーターが導入されます。 指数関数とは異なり、ラプラス分布は実際の数値軸全体で定義されます。
どこで
スケールパラメーターであり、 
-シフトパラメーター。
期待と分散：
正規分布よりも裾が重いため、ラプラス分布はエネルギー部門でのある種の測定誤差のモデル化に使用され、物理学、経済学、金融統計、通信などでも使用されます。
スキームに
二階
ワイブル分布
（ ここから取られます ）
ワイブル分布は、次の形式の確率密度関数によって記述されます。
どこで
（ > 0）は、イベントの強度（ 指数分布パラメーターに類似）であり、 -非定常性の指標（ 
） で 
、ワイブル分布は指数分布に縮退し、他の場合では、非定常強度の独立したイベントのフローを記述します。 で 
時間の経過とともに強度が増加するイベントのストリームがシミュレートされ、 
-減少している。 確率密度分布関数の領域：非負の実数。
したがって、ワイブル分布は、非定常イベント強度の場合の指数分布の一般化です。 信頼性の理論、技術のモデリングプロセス、天気予報、研削プロセスの説明などで使用されます。
ワイブル分布の期待値と分散：
どこで
-オイラーのガンマ関数。
スキームに
二階
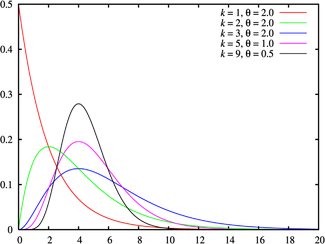
ガンマ分布（Erlang分布）
（ ここから取られます ）
ガンマ分布は、 カイ二乗分布の一般化であり、したがって、 指数分布です。 正規分布量の平方和、およびカイ二乗 分布と指数分布に分布する値の合計はガンマ分布になります。
ガンマ分布は、第3種のピアソン分布です 。 ガンマ分布の領域は、非負の自然数です。
ガンマ分布は、2つの非負パラメーターによって決定されます
-自由度の数（自由度の値全体に対して、ガンマ分布はアーラン分布と呼ばれます）およびスケール係数 
。
ガンマ分布は無限に割り切れます：量が
そして 分布がある 
そして 
したがって、量 
分布があります 
どこで
-オイラーのガンマ関数。
期待と分散：
ガンマ分布は、イベントの複雑な流れ、イベント間の時間間隔の合計、経済学、キューイング理論、およびロジスティックスをモデル化するために広く使用され、医学の平均余命を説明します。 これは、離散的な負の二項分布のユニークな類似物です。
スキームに
二階
ベータ配布
（ ここから取られます ）
項がガンマ分布を持つランダム変数である場合、ベータ分布は、それぞれに起因する2つの項の合計の割合を表します。 つまり、量が
そして 
ガンマ分布、値を持っています 
そして 
ベータ版が配布されます。
明らかに、ベータ配布ドメイン
。 ベータ分布は、 ピアソンタイプIの分布です。
パラメータはどこですか
そして -正の自然数、 
-オイラーのベータ関数。
期待と分散：
スキームに
二階
結論の代わりに
私の意見では、最も一般的な統計アプリケーションのほとんどをカバーする15の確率分布を調べました。
最後に、小さな宿題：為替取引システムの信頼性を評価するために、利益率などの指標が使用されます。 利益率は、総損失に対する総収入の比率として計算されます。 明らかに、収入を生成するシステムの場合、利益要因は複数であり、その値が高いほど、システムの信頼性は高くなります。
質問：利益要因はどのような分布ですか？
このテーマに関する私の考えを次の記事で紹介します。
PSこの記事の番号付き数式を参照する場合は、次のリンクを使用できます： article_link #x_y_z、ここで（xyz）は参照している数式の番号です。