C ++テンプレートでの導関数の分析計算

ここで先日、彼らは派生物の分析的発見について書いた。それは私の小さなC ++ライブラリの1つを思い起こさせた。









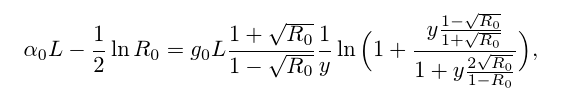
利益はいくらですか？ 答えは簡単です：かなり複雑な関数の最小値を見つけて、紙の上のペンが怠inessだったので、パラメーターによってこの関数の導関数を取得し、コードを書くときに封印されていないことを確認し、このコードが二重に怠maintainであることを確認しなければならなかったので、書くことにしました私のためにそれをすること。 さて、コードに次のようなものを書くために：

using Formula_t = decltype (k * (_1 - r0) / (_1 + r0) * (g0 / (alpha0 - logr0 / Num<300>) - _1)); //   const auto residual = Formula_t::Eval (datapoint) - knownValue; //   //   : const auto dg0 = VarDerivative_t<Formula_t, decltype (g0)>::Eval (datapoint); const auto dalpha0 = VarDerivative_t<Formula_t, decltype (alpha0)>::Eval (datapoint); const auto dk = VarDerivative_t<Formula_t, decltype (k)>::Eval (datapoint);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ワニの代わりに、最初に絵の中で偏微分関数を取得すると判明します（あるいは、単純化したバージョンですが、それほど怖くはありません）。



また、対応する派生物と関数が手書きで書かれているかのようにコンパイラが最適化するように十分に確認することも良いことです。 そして、私は確実にしたい-あなたは何度も最小値を見つけなければならなかった（実際には何億から10億のどこか、これはある種の計算実験の本質だった）ので、微分の計算はボトルネックになり、実行時に起こるだろう-ツリー構造での再帰。 実際にコンパイル中に派生物を計算するようコンパイラーに強制する場合、結果のコードに従ってオプティマイザーによって渡される可能性があり、すべての派生物を手動で書き出すことに比べて失われません。 ちなみにチャンスは実現しました。



カットの下-それがどのように機能するかの簡単な説明。



プログラムで関数を提示することから始めましょう。 何らかの理由で、すべての関数が型であることが起こりました。 関数は式ツリーでもあり、このツリーのNode



はNode



タイプで表されます。

 template<typename NodeClass, typename... Args> struct Node;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、 NodeClass



はノードのタイプ（変数、数値、単項関数、バイナリ関数）、 NodeClass



はこのノードのパラメーター（変数インデックス、数値、子ノード）です。



ノードは、自由変数とパラメーターの特定の値について、自身を区別し、印刷し、計算できます。 したがって、通常の番号を持つノードを表すためにタイプが定義されている場合：

 using NumberType_t = long long; template<NumberType_t N> struct Number {};
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

数値のノードの特殊化は簡単です：

 template<NumberType_t N> struct Node<Number<N>> { template<char FPrime, int IPrime> using Derivative_t = Node<Number<0>>; static std::string Print () { return std::to_string (N); } template<typename Vec> static typename Vec::value_type Eval (const Vec&) { return N; } constexpr Node () {} };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

任意の変数に関する任意の数の導関数はゼロです（ Derivative_t



型がこれを担当します。とりあえず、テンプレートパラメーターはそのままにします）。 数字の印刷も簡単です（ Print()



参照）。 数値でノードを計算します-この数値を返します（ Eval()



参照してください、 Vec



テンプレートパラメータについては後述します）。



変数は同様の方法で表示されます。

 template<char Family, int Index> struct Variable {};
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、 Family



とIndex



は「ファミリー」と変数のインデックスです。 だから それらは'w'



と1



に等しくなり、 -それぞれ'x'



および2



。



変数のノードは、数値のノードよりも少し興味深いものに決定されます。

 template<char Family, int Index> struct Node<Variable<Family, Index>> { template<char FPrime, int IPrime> using Derivative_t = std::conditional_t<FPrime == Family && IPrime == Index, Node<Number<1>>, Node<Number<0>>>; static std::string Print () { return std::string { Family, '_' } + std::to_string (Index); } template<typename Vec> static typename Vec::value_type Eval (const Vec& values) { return values (Node {}); } constexpr Node () {} };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

したがって、それに関する変数の導関数は1に等しく、その他の場合はゼロになります。 実際、 Derivative_t



型のFPrime



およびIPrime



は、 Derivative_t



物を取得する変数のファミリーおよびインデックスです。



1つの変数で構成される関数の値の計算は、値ディクショナリでの検索結果に還元され、 Eval()



関数に渡されます。 辞書自体は、その型によって目的の変数の値を見つけることができるため、変数の型をそれに渡し、対応する値を返すだけです。 辞書がこれをどのように行うかについては、後で検討します。



単項関数を使用すると、事態はさらに面白くなります。

 enum class UnaryFunction { Sin, Cos, Ln, Neg }; template<UnaryFunction UF> struct UnaryFunctionWrapper;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

UnaryFunctionWrapper



特殊化では、特定の各単項関数の導関数を取得するロジックをプッシュします。 コードの重複を最小限に抑えるために、引数に関する単項関数の導関数を使用します。チェーンルールを介してターゲット変数に関する引数をさらに区別するには、呼び出し元のコードが責任を負います。

 template<> struct UnaryFunctionWrapper<UnaryFunction::Sin> { template<typename Child> using Derivative_t = Node<Cos, Child>; }; template<> struct UnaryFunctionWrapper<UnaryFunction::Cos> { template<typename Child> using Derivative_t = Node<Neg, Node<Sin, Child>>; }; template<> struct UnaryFunctionWrapper<UnaryFunction::Ln> { template<typename Child> using Derivative_t = Node<Div, Node<Number<1>>, Child>; }; template<> struct UnaryFunctionWrapper<UnaryFunction::Neg> { template<typename> using Derivative_t = Node<Number<-1>>; };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、ノード自体は次のとおりです。

 template<UnaryFunction UF, typename... ChildArgs> struct Node<UnaryFunctionWrapper<UF>, Node<ChildArgs...>> { using Child_t = Node<ChildArgs...>; template<char FPrime, int IPrime> using Derivative_t = Node<Mul, typename UnaryFunctionWrapper<UF>::template Derivative_t<Child_t>, typename Node<ChildArgs...>::template Derivative_t<FPrime, IPrime>>; static std::string Print () { return FunctionName (UF) + "(" + Node<ChildArgs...>::Print () + ")"; } template<typename Vec> static typename Vec::value_type Eval (const Vec& values) { const auto child = Child_t::Eval (values); return EvalUnary (UnaryFunctionWrapper<UF> {}, child); } };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

チェーンルールを介して派生物を検討します-恐ろしく見えますが、アイデアは単純です。 計算も簡単です。子ノードの値を計算し、 EvalUnary()



関数を使用してこの値の単項関数の値を計算します。 むしろ、関数のファミリー：関数の最初の引数は、コンパイル時に目的のオーバーロードの選択を保証する単項関数を定義する型です。 はい、 UF



値自体を渡すことができ、スマートコンパイラはほぼ確実に必要なすべての定数伝搬パスを行いますが、ここでは安全にプレイする方が簡単です。



ちなみに、別の単項否定演算を導入することはできず、乗算をマイナス1に置き換えました。



バイナリノードではすべてが類似しており、派生物のみが絶対に怖いように見えます。 除算の場合、たとえば：

 template<> struct BinaryFunctionWrapper<BinaryFunction::Div> { template<char Family, int Index, typename U, typename V> using Derivative_t = Node<Div, Node<Add, Node<Mul, typename U::template Derivative_t<Family, Index>, V >, Node<Neg, Node<Mul, U, typename V::template Derivative_t<Family, Index> > > >, Node<Mul, V, V > >; };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、目的のメタ関数VarDerivative_t



が非常に簡単に定義されます。実際には、渡されたノードでのみDerivative_t



を呼び出すためです。

 template<typename Node, typename Var> struct VarDerivative; template<typename Expr, char Family, int Index> struct VarDerivative<Expr, Node<Variable<Family, Index>>> { using Result_t = typename Expr::template Derivative_t<Family, Index>; }; template<typename Node, typename Var> using VarDerivative_t = typename VarDerivative<Node, std::decay_t<Var>>::Result_t;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ヘルパー変数とタイプを定義すると、たとえば：

 //       : using Sin = UnaryFunctionWrapper<UnaryFunction::Sin>; using Cos = UnaryFunctionWrapper<UnaryFunction::Cos>; using Neg = UnaryFunctionWrapper<UnaryFunction::Neg>; using Ln = UnaryFunctionWrapper<UnaryFunction::Ln>; using Add = BinaryFunctionWrapper<BinaryFunction::Add>; using Mul = BinaryFunctionWrapper<BinaryFunction::Mul>; using Div = BinaryFunctionWrapper<BinaryFunction::Div>; using Pow = BinaryFunctionWrapper<BinaryFunction::Pow>; // variable template  C++14      : template<char Family, int Index = 0> constexpr Node<Variable<Family, Index>> Var {}; //   x0  , ,    : using X0 = Node<Variable<'x', 0>>; constexpr X0 x0; //       //   ,     : constexpr Node<Number<1>> _1; //  ,     ,  : template<typename T1, typename T2> Node<Add, std::decay_t<T1>, std::decay_t<T2>> operator+ (T1, T2); template<typename T1, typename T2> Node<Mul, std::decay_t<T1>, std::decay_t<T2>> operator* (T1, T2); template<typename T1, typename T2> Node<Div, std::decay_t<T1>, std::decay_t<T2>> operator/ (T1, T2); template<typename T1, typename T2> Node<Add, std::decay_t<T1>, Node<Neg, std::decay_t<T2>>> operator- (T1, T2); //   ,      : template<typename T> Node<Sin, std::decay_t<T>> Sin (T); template<typename T> Node<Cos, std::decay_t<T>> Cos (T); template<typename T> Node<Ln, std::decay_t<T>> Ln (T);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

投稿の最初からコードを書くことができます。



残っているものは何ですか？



最初に、 Eval()



関数に渡される型を処理します。 第二に、あるサブツリーを別のサブツリーに置き換えることで、希望する式を変換できる可能性に言及します。 2つ目から始めましょう。簡単です。



動機（スキップ可能）：現在のバージョンで動作するコードをわずかにプロファイルすると、計算に時間がかかることがわかります。 一般的に言えば、これは各実験ポイントで同じです。 関係ありません！ 各実験ポイントで式の値を計算する前に一度計算した個別の変数を導入し、すべての出現を置き換えます この変数に（実際、最初の動機付けコードでは、これは既に行われています）。 ただし、 私たちはそれを覚えておく必要があります 一般的に言えば、無料のパラメータではなく、 。 思い出すのは非常に簡単です：私たちは置き換えます に （このために、 ApplyDependency_t



メタ関数がApplyDependency_t



れますが、 Rewrite_t



またはそのようなものを呼び出すRewrite_t



がRewrite_t



正確です）、区別して返します に 戻る：

 using Unwrapped_t = ApplyDependency_t<decltype (logr0), decltype (Ln (r0)), Formula_t>; using Derivative_t = VarDerivative_t<Unwrapped_t, decltype (r0)>; using CacheLog_t = ApplyDependency_t<decltype (Ln (r0)), decltype (logr0), Derivative_t>;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

実装は冗長ですが、イデオロギー的に単純です。 フォーミュラツリーを再帰的に下降させ、テンプレートと完全に一致する場合はツリー要素を置き換えます。そうでなければ、何も変更しません。 合計で、3つの専門化があります：単項関数の子ノードに沿った降下、バイナリ関数の子ノードに沿った降下、および実際の置換がありますが、子ノードに沿った降下の特殊化は、テンプレートが考慮中のサブ関数に対応するサブツリーと一致しないことを確認する必要があります：

 template<typename Var, typename Expr, typename Formula, typename Enable = void> struct ApplyDependency { using Result_t = Formula; }; template<typename Var, typename Expr, typename Formula> using ApplyDependency_t = typename ApplyDependency<std::decay_t<Var>, std::decay_t<Expr>, Formula>::Result_t; template<typename Var, typename Expr, UnaryFunction UF, typename Child> struct ApplyDependency<Var, Expr, Node<UnaryFunctionWrapper<UF>, Child>, std::enable_if_t<!std::is_same<Var, Node<UnaryFunctionWrapper<UF>, Child>>::value>> { using Result_t = Node< UnaryFunctionWrapper<UF>, ApplyDependency_t<Var, Expr, Child> >; }; template<typename Var, typename Expr, BinaryFunction BF, typename FirstNode, typename SecondNode> struct ApplyDependency<Var, Expr, Node<BinaryFunctionWrapper<BF>, FirstNode, SecondNode>, std::enable_if_t<!std::is_same<Var, Node<BinaryFunctionWrapper<BF>, FirstNode, SecondNode>>::value>> { using Result_t = Node< BinaryFunctionWrapper<BF>, ApplyDependency_t<Var, Expr, FirstNode>, ApplyDependency_t<Var, Expr, SecondNode> >; }; template<typename Var, typename Expr> struct ApplyDependency<Var, Expr, Var> { using Result_t = Expr; };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ふう。 パラメーター値の転送を処理するために残ります。



各パラメーターには独自の型があるため、それぞれが対応する値を返すパラメーターの型でオーバーロードされた関数のファミリを構築すると、再び（少し前の単項関数の計算と同様に）コンパイラがこのビジネスを崩壊させる可能性があります最適化します（そして、偶然、そして、賢い女の子を最適化します）。 さて、次のようなもの：

 auto GetValue (Variable<'x', 0>) { return value_for_x0; } auto GetValue (Variable<'x', 1>) { return value_for_x1; } ...
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

私たちだけが美しく書きたいので、たとえば次のように書くことができます。

 BuildFunctor (g0, someValue, alpha0, anotherValue, k, yetOneMoreValue, r0, independentVariable, logr0, logOfTheIndependentVariable);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、 g0



、 alpha0



およびcompanyは、対応する変数のタイプとそれに続く対応する値を持つオブジェクトです。



comp-timeでパラメータータイプが指定され、ランタイムで値が指定される関数の一般的な形式を作成することで、どのようにハリネズミとハリネズミを横切ることができますか？ ラムダは救助に駆けつけます！

 template<typename ValueType, typename NodeType> auto BuildFunctor (NodeType, ValueType val) { return [val] (NodeType) { return val; }; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このような関数が2つあるとします。1つの名前空間で関数のファミリを取得して、オーバーロードによって目的の関数を選択するにはどうすればよいでしょうか。 相続は救助に急ぎます！

 template<typename F, typename S> struct Map : F, S { using F::operator(); using S::operator(); Map (F f, S s) : F { std::forward<F> (f) } , S { std::forward<S> (s) } { } };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

私たちは両方のラムダから継承し（結局、ラムダはコンパイラによって生成された名前を持つ構造に展開されます。つまり、ラムダはそれから継承できます）、それらの演算子括弧をスコープに入れます。



さらに、ラムダからだけでなく、括弧演算子を含む任意の構造からも継承することができます。 おっと、代数を得た。 したがって、N個のラムダがある場合、最初の2つのラムダから最初のMap



、最初のMap



からの次のMap



、次のラムダなどを継承できます。 コードの形式にしましょう。

 template<typename F> auto Augment (F&& f) { return f; } template<typename F, typename S> auto Augment (F&& f, S&& s) { return Map<std::decay_t<F>, std::decay_t<S>> { f, s }; } template<typename ValueType> auto BuildFunctor () { struct { ValueType operator() () const { return {}; } using value_type = ValueType; } dummy; return dummy; } template<typename ValueType, typename NodeType, typename... Tail> auto BuildFunctor (NodeType, ValueType val, Tail&&... tail) { return detail::Augment ([val] (NodeType) { return val; }, BuildFunctor<ValueType> (std::forward<Tail> (tail)...)); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

完全性と一意性を自動的に取得します。一部の引数が指定されていない場合、一部の引数が2回指定されている場合と同様に、これはコンパイルエラーになります。



実際には、それだけです。



私の意見では、その時に見せてくれた友人の一人がconstexpr関数のよりエレガントな解決策を提案していなかったとしても、今のところ9か月間到達していません。



さて、図書館へのリンク： I Am Madです。 生産の準備ができていないため、プルリクエストは受け入れられます。



さて、テンプレートの上にあるラムダの上にあるテンプレートの上にあるテンプレートのこれらのレイヤーを通過し、かなり最適なコードを生成できる現代のコンパイラーがどれほどスマートか疑問に思うでしょう。