ストックホルム市立図書館。 写真ミノタウリア。

この記事では、メモリアクセス時間をO（1）として評価することは非常に悪い考えであり、代わりにO（√N）を使用する必要があることについてお話したいと思います。まず、問題の実際的な側面を検討し、次に理論物理学に基づいて数学的な側面を検討し、次に結果と結論を検討します。

はじめに

コンピューターサイエンスとアルゴリズムの複雑さの分析を勉強した場合、リンクリストの通過はO（N）、バイナリ検索はO（log（N））、ハッシュテーブルの要素の検索はO（1）であることがわかります。これがすべて真実ではないと言ったらどうでしょうか？リンクリストの通過が実際にO（N√N）であり、ハッシュテーブルの検索がO（√N）である場合はどうなりますか？

信じられない？私は今あなたを説得します。メモリへのアクセスはO（1）ではなく、O（√N）であることを示します。この結果は、理論的にも実際的にも有効です。練習から始めましょう。

測定する

最初に定義を決めましょう。「O」表記は、メモリの使用から命令の実行まで、多くのものに適用できます。この記事のフレームワークでは、O（f（N））は、Nバイトのメモリ（または同じサイズのN個の要素）にアクセスするために必要な時間の上限（最悪の場合）を意味します） Big Oを使用して時間を分析しますが、操作は分析しません 。これは重要です。中央処理装置が低速のメモリを長時間待機していることがわかります。個人的には、プロセッサが待機中に何をするかは気にしません。私は時間、このタスクまたはそのタスクにかかる時間のみを気にしているので、上記の定義に限定しています。

別の注意：ヘッダー内のRAMは、一般にランダムアクセス（ランダムメモリアクセス）を意味し、特定の種類のメモリではありません。キャッシュ、DRAM、またはスワップに関係なく、メモリ内の情報のアクセス時間を考慮します。

これは、サイズNのリンクリストを通過する単純なプログラムです。サイズ-64アイテムから4億2,000万アイテムまで。リストの各ノードには、64ビットポインターと64ビットのデータが含まれています。ノードはメモリ内で混在しているため、すべてのメモリアクセスは任意です。リストの通過を数回測定し、要素にアクセスするのにかかった時間をグラフにマークします。 O（1）の形のフラットグラフを取得する必要があります。実際に起こることは次のとおりです。

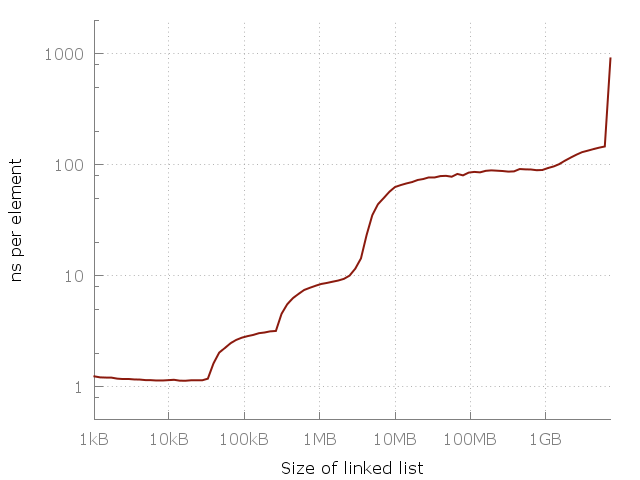
リンクリスト内のアイテムにアクセスするのが難しい。 100メガバイトのリスト内の任意の要素へのアクセスは、10キロバイトのリスト内の要素へのアクセスよりも約100倍遅くなります。

このグラフは両方の軸で対数目盛を使用しているため、実際にはその差は非常に大きいことに注意してください。 1要素あたり約1ナノ秒から、マイクロ秒に到達しました！しかし、なぜですか？もちろん、答えはキャッシュです。システムメモリ（RAM）は実際には非常に遅いため、スマートコンピューターの設計者はこれを補うために、高速で、より近く、より高価なキャッシュの階層を追加して、操作を高速化します。私のコンピューターには、それぞれL1、L2、L3 32 KB、256 KB、4 MBの3つのレベルのキャッシュがあります。私は8ギガバイトのRAMを持っていますが、この実験を実行したとき、空きギガバイトが6つしかなかったため、最後に開始したのはディスクへのスワップ（SSD）でした。同じグラフですが、キャッシュサイズがあります。

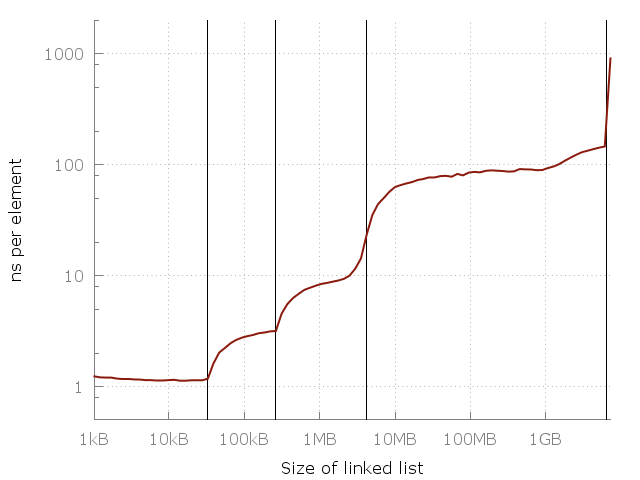
縦線は、L1 = 32 kb、L2 = 256 kb、L3 = 4 mb、および6ギガバイトの空きメモリを示しています。

このグラフは、キャッシュの重要性を示しています。各キャッシュレイヤーは、前のレイヤーよりも数倍高速です。これは、スマートフォン、ラップトップ、メインフレームなど、最新のCPUアーキテクチャの現実です。しかし、一般的なパターンはどこにありますか？このグラフに簡単な方程式を配置できますか？できることがわかった！

よく見てみましょう。1メガバイトから100メガバイトの間で、約10倍の速度低下があります。そして、100メガバイトから10ギガバイトまで同じです。使用メモリが100倍増加するごとに、10倍の速度低下が発生するようです。これをチャートに追加しましょう。

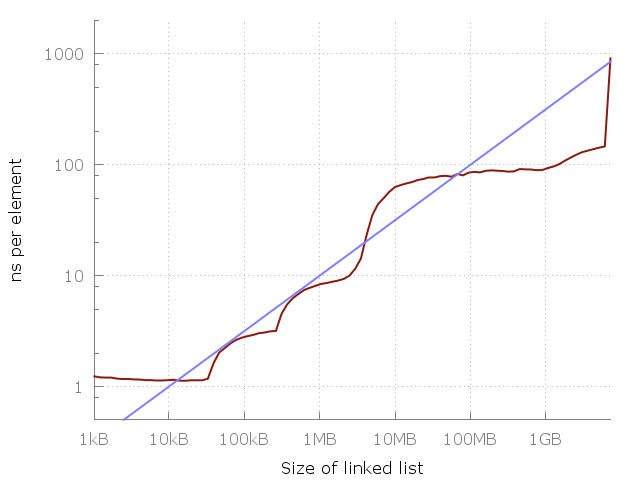
青い線はO（√N）です。

このグラフの青い線は、各メモリアクセスのO（√N）コストを示しています。いいですね。もちろん、これは私の特定の車であり、あなたの写真は異なって見えるかもしれません。ただし、方程式は覚えやすいので、大まかなルールとして使用する必要があります。

あなたはおそらく、スケジュールの右側に、次は何を求めているのでしょうか？上昇は続くのでしょうか、それともチャートはフラットになりますか？まあ、しばらくはフラットになりますが、SSDには十分な空き領域がありますが、その後、プログラムはHDD、ディスクサーバー、遠くのデータセンターなどに切り替える必要があります。各ジャンプは新しい平坦な領域を作成しますが、一般的な上昇傾向は続くと思います。時間の不足と大規模なデータセンターへのアクセス不足のため、実験を続行しませんでした。

「しかし、経験的手法をBig-O境界の定義に使用することはできません」とあなたは言います。もちろん！メモリへのアクセスの遅延に理論的な制限があるのでしょうか？

ラウンドライブラリ

思考実験について説明しましょう。あなたが循環図書館で働いている司書だとします。テーブルは中央にあります。本を入手するのに必要な時間は、旅行に必要な距離によって制限されます。そして最悪の場合、これは半径です。なぜなら、あなたはライブラリのまさに端に到達する必要があるからです。

あなたの妹が別の同様の図書館で働いていると仮定しますが、彼女（彼女の姉妹ではなく、図書館:)、-約。 per。）半径は2倍です。時には彼女は2倍行く必要があります。しかし、彼女のライブラリには、あなたのライブラリの4倍の領域があり、そこには4倍の本が含まれています。本の数は、半径の二乗に比例します：N∝r²。また、本のアクセス時間Tは半径に比例するため、N∝T²またはT∝√NまたはT = O（√N）です。

これは、そのライブラリ（RAM）からデータを取得する必要がある中央処理装置との大まかな類似点です。もちろん、「司書」の速度は重要ですが、ここでは光の速度によって制限されています。たとえば、3 GHzプロセッサの1サイクルでは、ライトは10 cmの距離を移動するため、ラウンドトリップの場合、瞬時に利用可能なメモリはプロセッサから5センチ以内にある必要があります。

さて、プロセッサから一定の距離r内にどれだけの情報を配置できますか？上記のラウンドフラットライブラリについて説明しましたが、球状の場合はどうでしょうか。球に収まるメモリの量は、半径の立方体-r³に比例します。実際には、コンピューターは非常にフラットです。これは、一部はフォームファクターの問題であり、一部は冷却の問題です。おそらくいつか、メモリの3次元ブロックを作成して冷却する方法を学習しますが、これまでのところ、半径r内の情報量Nの実際的な制限はN ∝r²になります。これは、データセンター（惑星の2次元表面に分散している）などの非常に離れたストレージに当てはまります。

しかし、理論的には状況を改善することは可能ですか？これを行うには、ブラックホールと量子物理学について少し学ぶ必要があります。

理論的境界

半径rの球に配置できる情報量は、ベッケンシュタイン境界を使用して計算できます。この量は、半径と質量に直接比例します：N ∝ r・m。球はどれくらいの大きさですか？さて、宇宙で最も密度の高いものは何ですか？ブラックホール！ブラックホールの質量は半径に比例することがわかります：m ∝ r。つまり、半径rの球に配置できる情報の量はN ∝r²です。情報の量は、ボリュームではなく、球体の面積によって制限されるという結論に達しました！

つまり、非常に大きなL1キャッシュをプロセッサに配置しようとすると、最終的にブラックホールに陥り、計算結果がユーザーに返されなくなります。

N ∝r²は実用的であるだけでなく、理論的な境界でもあることがわかります。つまり、物理法則はメモリへのアクセス速度に制限を設定します。Nビットのデータを取得するには、O（√N）に比例する距離にメッセージを送信する必要があります。つまり、タスクが100倍増加すると、1つの要素へのアクセス時間が10倍増加します。そして、これはまさに私たちの実験が示したものです！

ちょっとした歴史

過去には、プロセッサはメモリよりもはるかに低速でした。平均して、メモリ検索は計算自体よりも高速でした。正弦および対数のテーブルをメモリに保存することは一般的な方法でした。しかし、時代は変わりました。プロセッサのパフォーマンスは、メモリの速度よりもはるかに速く成長しました。最新のプロセッサのほとんどは、メモリを待つだけです。これがキャッシュのレベルが非常に多い理由です。この傾向は今後も続くと思いますので、古い真実を再考することが重要です。

Big-Oのすべてのポイントは抽象化にあると言えます。メモリ遅延などのアーキテクチャの詳細を取り除く必要があります。これは本当ですが、 O（1）は間違った抽象化であると主張します。特に、定数要素を抽象化するにはBig-Oが必要ですが、メモリアクセスは一定の操作ではありません。理論的にも実践的にも。

過去には、コンピュータのメモリへのアクセスはどれも同じくらい高価でしたので、O（1）です。しかし、これはもはや事実ではありません。別の方法で考え、O（1）のメモリアクセスを忘れ、O（√N）に置き換える時が来たと思います。

結果

メモリにアクセスするコストは、要求されるサイズ-O（√N）に依存します。Nは、各要求でアクセスされるメモリのサイズです。したがって、同じリストまたはテーブルに対して呼び出しが発生した場合、次のステートメントは真になります。

リンクされたリストを通過することは、O（N√N）操作です。バイナリ検索はO（√N）です。連想配列からの取得はO（√N）です。実際、 データベース内の任意の検索は最高でO（√N）です。

操作間で実行されるアクションが重要であることは注目に値します。プログラムがサイズNのメモリで動作する場合、任意のメモリ要求はO（√N）になります。したがって、サイズKのリストを調べるとO（K√N）かかります。繰り返し通過すると（すぐに、別のメモリに頼らずに）、コストはO（K√K）になります。これは重要な結論です。 同じメモリロケーションに複数回アクセスする必要がある場合は、 呼び出しの間隔を最小化します 。

サイズKの配列をパスする場合、最初の呼び出しのみが任意であるため、コストはO（√N+ K）になります。再パスはO（K）になります。したがって、別の重要な結論： パスを作成する場合は、配列を使用します。

大きな問題が1つあります。多くの言語は実際の配列をサポートしていません。 Javaなどの言語や多くのスクリプト言語は、すべてのオブジェクトを動的メモリに格納します。実際の配列は、ポインターの配列です。このような配列を通過する場合、リンクリストを通過するときよりもパフォーマンスは向上しません。 Javaのオブジェクトの配列を調べるにはO（K√N）かかります 。これは、正しい順序でオブジェクトを作成することで補うことができます。メモリアロケーターは、オブジェクトを順番にメモリに配置することを望みます。しかし、異なる時間にオブジェクトを作成したり、それらを混合する必要がある場合は、何も機能しません。

おわりに

メモリアクセス方法は非常に重要です。常に予測可能な方法でメモリにアクセスし、任意のメモリアクセスを最小限に抑えるようにしてください。もちろん、ここには新しいものはありませんが、繰り返す価値はあります。キャッシュについて考えるための新しいツールを採用することを望みます。メモリコストへのアクセスO（√N）。 次に複雑さを評価するときは、この考えを覚えておいてください。

RAMとOの神話（1）