前のパートでは、勾配降下法と呼ばれる最適化アルゴリズムの解析を開始しました。 前の記事は、バッチ勾配降下法と呼ばれるアルゴリズムの変形を書くことで終わりました。
アルゴリズムの別のバージョン-確率的勾配降下法があります。 確率的=ランダム。
,
{
for i in train_set
{

}
}
また、バッチがどのように見えるかを思い出させます。
,
{

}
式は似ていますが、ご覧のように、バッチ勾配降下は一度にデータセット全体を使用して1つのステップを計算します。一方、確率的ステップはステップごとに1つの要素しか使用しません。 これらの2つのオプションを組み合わせて、ミニバッチ(ミニバッチ)降下を取得することができます。これは、一度にすべてまたは1つではなく、100個の要素を処理します。
これら2つのオプションは同じように動作しますが、同じではありません。 バッチ降下は、実際には最急降下の方向に続きますが、トレーニングセットの1つの要素のみを使用する確率降下では、サンプル全体の勾配を正しく計算できません。 この違いは、グラフィカルに説明する方が簡単です。 これを行うには、線形回帰係数が計算された最初の部分のコードを変更します。 コスト関数は次のとおりです。

ご覧のとおり、これはわずかに細長い放物面です。 また、彼の「トップビュー」では、クロスが分析的に見つかった真の最小値をマークしています。

まず、パケット降下の動作を検討します。
コード
def batch_descent(A, Y, speed=0.001): theta = np.array(INITIAL_THETA.copy(), dtype=np.float32) theta.reshape((len(theta), 1)) previous_cost = 10 ** 6 current_cost = cost_function(A, Y, theta) while np.abs(previous_cost - current_cost) > EPS: previous_cost = current_cost derivatives = [0] * len(theta) # --------------------------------------------- for j in range(len(theta)): summ = 0 for i in range(len(Y)): summ += (Y[i] - A[i]@theta) * A[i][j] derivatives[j] = summ # theta[0] += speed * derivatives[0] theta[1] += speed * derivatives[1] # --------------------------------------------- current_cost = cost_function(A, Y, theta) print("Batch cost:", current_cost) plt.plot(theta[0], theta[1], 'ro') return theta
バッチアニメーション 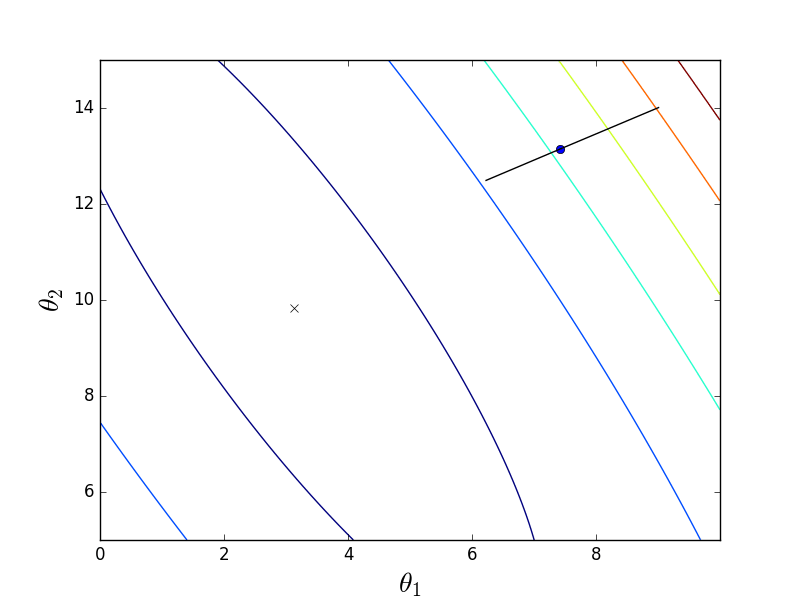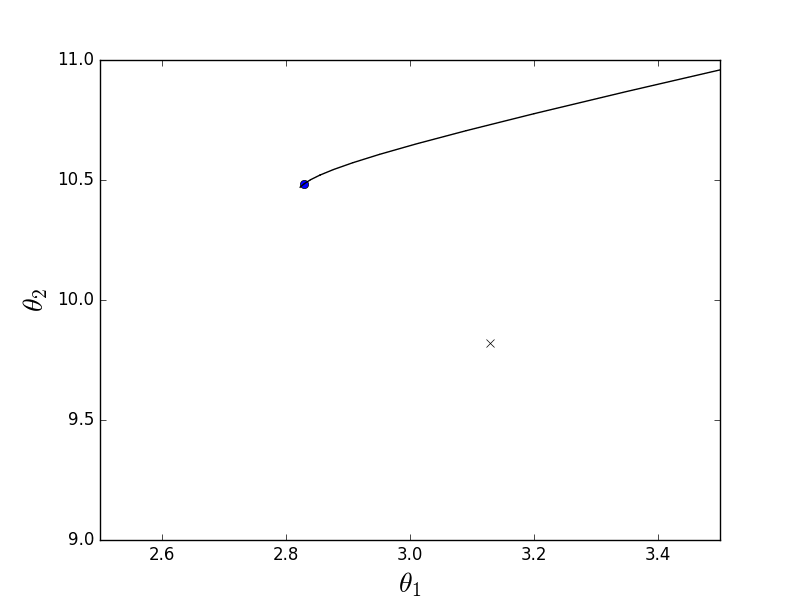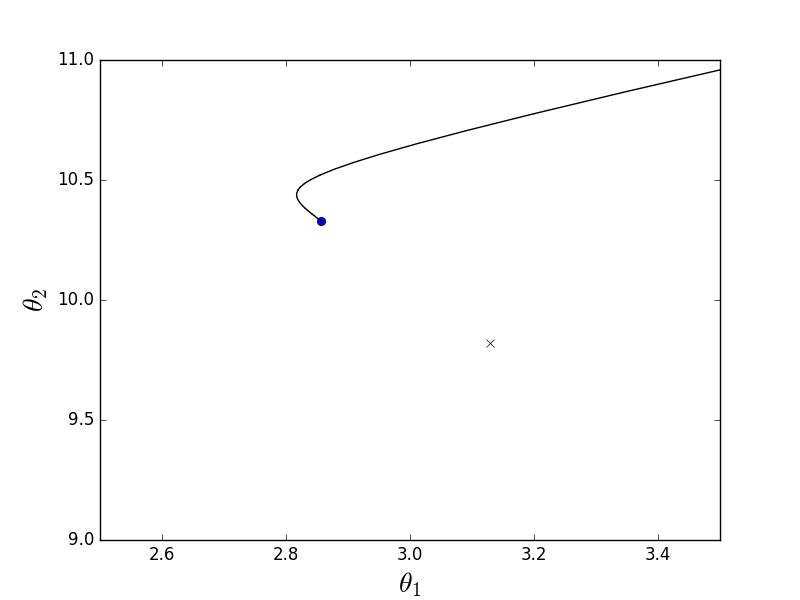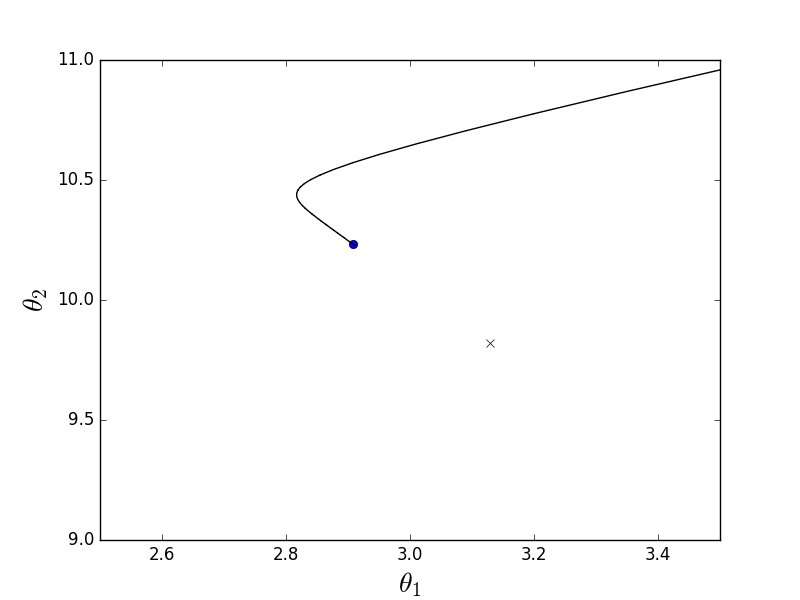

放物面が伸びているという事実により、「渓谷」はその「底」を通過し、そこに落ちます。 このため、この渓谷に沿った最後のステップは非常に小さいですが、それにもかかわらず、遅かれ早かれ勾配降下は最小に達します。 下降は反勾配線に沿って行われ、各ステップは最小に近づきます。
現在は同じ機能ですが、確率的降下の場合:
コード
def stochastic_descent(A, Y, speed=0.1): theta = np.array(INITIAL_THETA.copy(), dtype=np.float32) previous_cost = 10 ** 6 current_cost = cost_function(A, Y, theta) while np.abs(previous_cost - current_cost) > EPS: previous_cost = current_cost # -------------------------------------- # for i in range(len(Y)): i = np.random.randint(0, len(Y)) derivatives = [0] * len(theta) for j in range(len(theta)): derivatives[j] = (Y[i] - A[i]@theta) * A[i][j] theta[0] += speed * derivatives[0] theta[1] += speed * derivatives[1] current_cost = cost_function(A, Y, theta) print("Stochastic cost:", current_cost) plt.plot(theta[0], theta[1], 'ro') # -------------------------------------- current_cost = cost_function(A, Y, theta) return theta
定義では、1つの要素のみが選択されていると記述されています。このコードでは、後続の各要素がランダムに選択されます。
確率的アニメーション 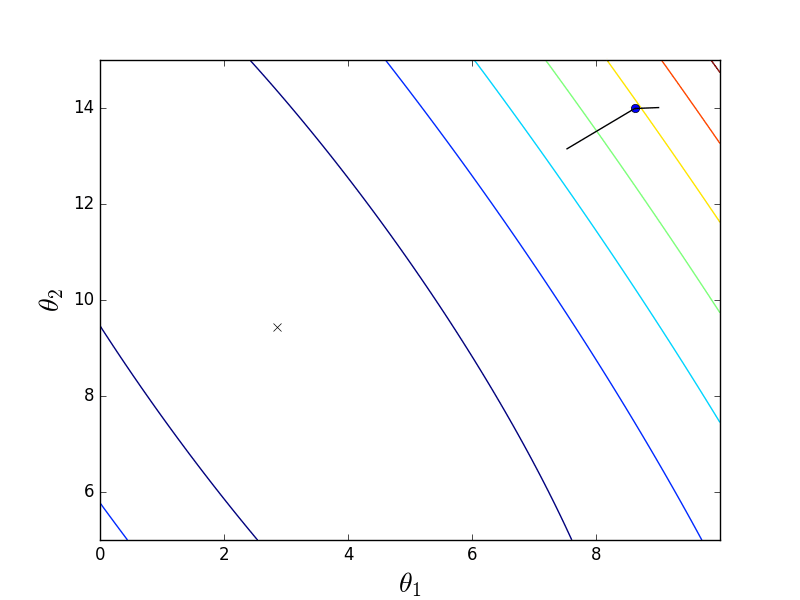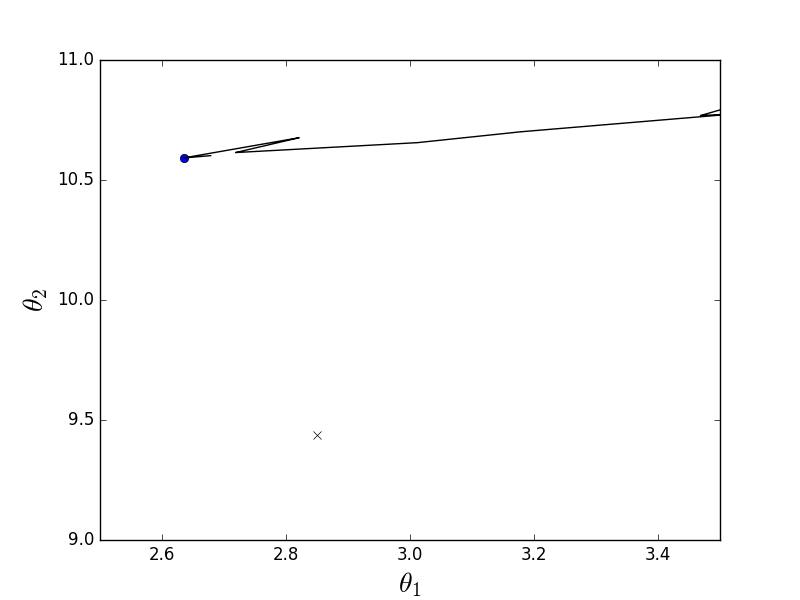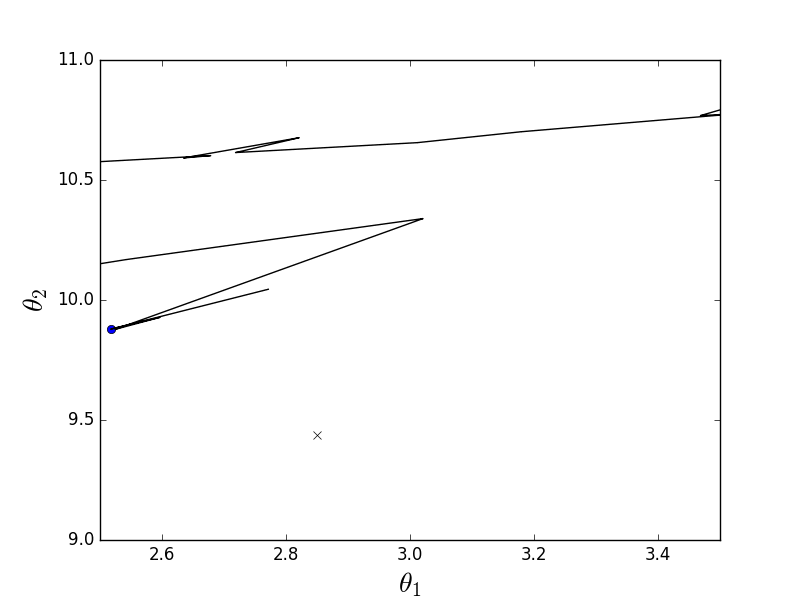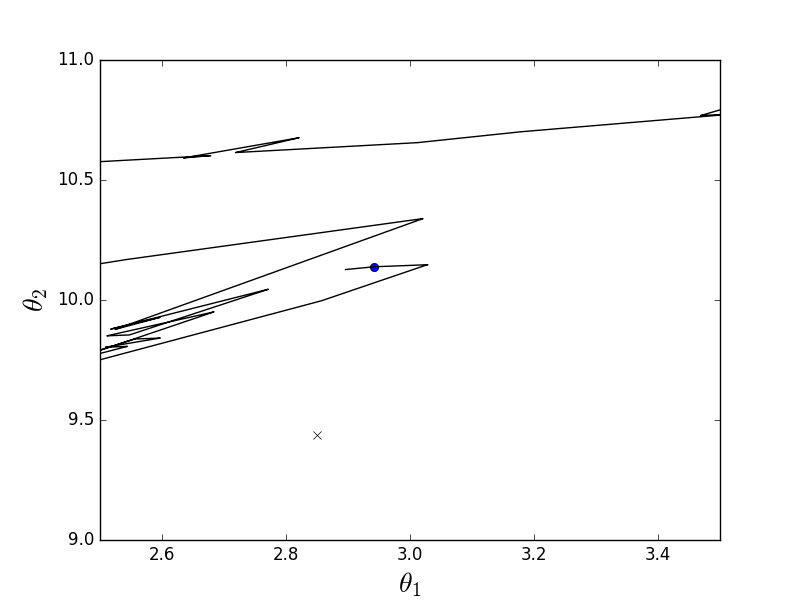

ご覧のように、確率的バリアントの場合、下降は反勾配線をたどりませんが、一般に、各ステップがランダムな方向にどのように逸脱するかは明確ではありません。 そのようなランダムなぎくしゃくした動きは偶然にしか最小化できないように思えるかもしれませんが、確率的勾配降下はほぼ確実に収束することが証明されました。 たとえば 、 いくつかの リンク 。
全コード
import numpy as np import matplotlib.pyplot as plt TOTAL = 200 STEP = 0.25 EPS = 0.1 INITIAL_THETA = [9, 14] def func(x): return 0.2 * x + 3 def generate_sample(total=TOTAL): x = 0 while x < total * STEP: yield func(x) + np.random.uniform(-1, 1) * np.random.uniform(2, 8) x += STEP def cost_function(A, Y, theta): return (Y - A@theta).T@(Y - A@theta) def batch_descent(A, Y, speed=0.001): theta = np.array(INITIAL_THETA.copy(), dtype=np.float32) theta.reshape((len(theta), 1)) previous_cost = 10 ** 6 current_cost = cost_function(A, Y, theta) while np.abs(previous_cost - current_cost) > EPS: previous_cost = current_cost derivatives = [0] * len(theta) # --------------------------------------------- for j in range(len(theta)): summ = 0 for i in range(len(Y)): summ += (Y[i] - A[i]@theta) * A[i][j] derivatives[j] = summ # theta[0] += speed * derivatives[0] theta[1] += speed * derivatives[1] # --------------------------------------------- current_cost = cost_function(A, Y, theta) print("Batch cost:", current_cost) plt.plot(theta[0], theta[1], 'ro') return theta def stochastic_descent(A, Y, speed=0.1): theta = np.array(INITIAL_THETA.copy(), dtype=np.float32) previous_cost = 10 ** 6 current_cost = cost_function(A, Y, theta) while np.abs(previous_cost - current_cost) > EPS: previous_cost = current_cost # -------------------------------------- # for i in range(len(Y)): i = np.random.randint(0, len(Y)) derivatives = [0] * len(theta) for j in range(len(theta)): derivatives[j] = (Y[i] - A[i]@theta) * A[i][j] theta[0] += speed * derivatives[0] theta[1] += speed * derivatives[1] # -------------------------------------- current_cost = cost_function(A, Y, theta) print("Stochastic cost:", current_cost) plt.plot(theta[0], theta[1], 'ro') return theta X = np.arange(0, TOTAL * STEP, STEP) Y = np.array([y for y in generate_sample(TOTAL)]) # , X = (X - X.min()) / (X.max() - X.min()) A = np.empty((TOTAL, 2)) A[:, 0] = 1 A[:, 1] = X theta = np.linalg.pinv(A).dot(Y) print(theta, cost_function(A, Y, theta)) import time start = time.clock() theta_stochastic = stochastic_descent(A, Y, 0.001) print("St:", time.clock() - start, theta_stochastic) start = time.clock() theta_batch = batch_descent(A, Y, 0.001) print("Btch:", time.clock() - start, theta_batch)
200の要素では、速度にほとんど差はありませんが、要素の数を2000(これも非常に小さい)に増やし、学習速度を調整すると、確率バージョンは必要に応じてバッチにヒットします。 ただし、確率的性質のため、メソッドが失敗することがあり、停止することができずに最小値近くで振動します。 このようなもの:

このため、純粋な実装は適用できません。 何らかの方法で秩序を呼び、「ランダム性」を減らすために、学習の速度を下げることができます。 実際には、ミニバッチバリエーションが使用されます。1つのランダムに選択された要素の代わりに複数が選択されるという点で、確率的バリエーションとは異なります。
これらの2つのアプローチの違い、プラスとマイナスについてかなり多く書かれていますが、簡単に要約します。
-バッチ降下は、グローバルまたはローカルを最小化することに自信を持って努力するため、厳密に凸関数に適しています。
-確率論は、多数の局所的最小値を持つ関数でより良く機能します-各ステップは、次の値が局所的ピットから「ノック」する可能性があり、最終的な解決策はバッチ降下よりも最適です。
-確率論はより速く計算されます-選択からのすべての要素がすべてのステップで必要なわけではありません。 サンプル全体がメモリに収まらない場合があります。 ただし、さらに手順が必要です。
-確率論では、作業中に新しい要素を簡単に追加できます(「オンライン」トレーニング)。
-ミニバッチの場合、コードをベクトル化することもできます。これにより、実行が大幅に高速化されます。
また、勾配降下には、運動量、最速降下、平均化、Adagrad、AdaDelta、RMSPropなど、多くの修正があります。 ここでは、いくつかの簡単な概要を見ることができます。 多くの場合、前のステップの勾配値を使用するか、特定のステップの最適な速度値を自動的に計算します。 OLSの単純で滑らかな関数にこれらの方法を使用してもあまり意味がありませんが、ニューラルネットワークおよび多数の層/ニューロンを持つネットワークの場合、コスト関数は完全に悲しくなり、最適なソリューションに到達せずに勾配降下がローカルウェルでスタックする可能性があります。 このような問題にはステロイド法が適しています。 以下は、最小化するのが簡単な関数の例です(OLSを使用した2次元線形回帰)。

そして、非線形関数の例:

勾配降下法は、1次の最適化手法(1次導関数)です。 多くの二次法もあります-二次導関数を計算してヘッセ行列を構築する必要があります(かなり高価な操作-
 ) たとえば、2次勾配降下(学習速度はヘッセ行列に置き換えられました)、BFGS、共役勾配、ニュートン法、および他の膨大な数の方法 。 一般に、最適化は個別の非常に広範な問題の層です。 ただし、これは Jan Lekunの 作品 + ビデオの 例(単なるプレゼンテーションですが)で、彼は、あなたは蒸気を流して勾配法を使用することはできないと言っています。 2007年のプレゼンテーションを考慮しても、大規模なANNを使用した最近の多くの実験では勾配法が使用されています。 たとえば 。
) たとえば、2次勾配降下(学習速度はヘッセ行列に置き換えられました)、BFGS、共役勾配、ニュートン法、および他の膨大な数の方法 。 一般に、最適化は個別の非常に広範な問題の層です。 ただし、これは Jan Lekunの 作品 + ビデオの 例(単なるプレゼンテーションですが)で、彼は、あなたは蒸気を流して勾配法を使用することはできないと言っています。 2007年のプレゼンテーションを考慮しても、大規模なANNを使用した最近の多くの実験では勾配法が使用されています。 たとえば 。
むき出しのサイクルではそれほど得られません-コードにはベクトル化が必要です。 ベクトル化の基本的なアルゴリズムはバッチ勾配降下です。
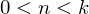 ここで、kはテストサンプルの要素数です。 したがって、ベクトル化はミニバッチ方式に適しています。 前回と同様に、開いたベクターにすべてを書きます。 最初の行列が転置されることに注意してください-
ここで、kはテストサンプルの要素数です。 したがって、ベクトル化はミニバッチ方式に適しています。 前回と同様に、開いたベクターにすべてを書きます。 最初の行列が転置されることに注意してください- 
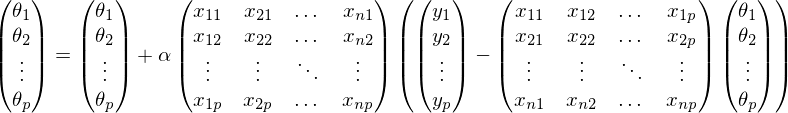
証明のために、反対方向にいくつかの手順を行ってみましょう。

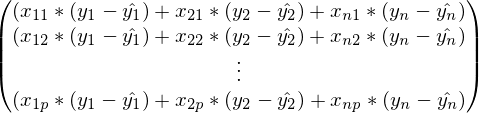
前の式では、各行でインデックスjが固定され、i-は1からnまで変化します。 金額を折り畳むことにより:
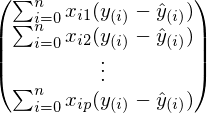
この式は、勾配降下法の定義とまったく同じです。 最後に、最後のステップはベクトルと行列の折りたたみです:

そのようなステップのコストは
 ここで、nは要素の数、pはフィーチャの数です。 はるかに良い
ここで、nは要素の数、pはフィーチャの数です。 はるかに良い 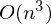 。 これと同じ式もあります。
。 これと同じ式もあります。

予測値と実際の値が入れ替わっていることに注意してください。これにより、学習速度の前で符号が変化します。
»必要な例を実行するには、numpy、matplotlibを使用します。
»記事で使用されている資料-github.com/m9psy/neural_network_habr_guide