目次
パート1-線形回帰
パート2-勾配降下
パート3-勾配降下の続き
はじめに
この投稿では、初心者向けのニューラルネットワークシリーズを開始します。 人工ニューラルネットワーク専用です（突然）。 サイクルの目的は、この数学的モデルを説明することです。 多くの場合、そのような記事を読んだ後、私は控えめな表現、誤解を感じました-国民議会は依然として「ブラックボックス」のままでした-一般的には、彼らはどのように配置されているか、彼らが何をしているか、そして入力データと出力データが知られています それにもかかわらず、完全で包括的な理解が不足しています。 また、非常に快適で便利な抽象化を備えた最新のライブラリは、「ブラックボックス」の感覚を高めるだけです。 これは間違いなく悪いとは言えませんが、使用したツールを理解するのに遅すぎることはありません。 したがって、私の主な目標は、ニューラルネットワークの構造を詳細に説明し、その構造について誰もまったく質問しないようにすることです。 NSが魔法のように見えないように。 これは数学的論文ではないので、説明的な図と例を提供して、いくつかの方法を単純な言語で記述することに限定しています（もちろん、式は除外しません）。
このサイクルは、読者の基本的な高等教育の数学レベルに合わせて設計されています。 コードはnumpy 1.11でPython3.5で記述されます。 その他のサポートライブラリのリストは、各投稿の最後にあります。 すべてがゼロから書き込まれます。 MNISTベースがテスト対象として選択されました-これらは、28 * 28ピクセルの手書き数字の白黒の中央画像です。 デフォルトでは、60,000個の画像がトレーニング用にマークされ、10,000個がテスト用にマークされています。 例では、デフォルトの配布を変更しません。
MNISTからの画像の例：
MNISTの構造に焦点を当てるのではなく、データベースをロードして目的の形式で保存するコードをレイアウトするだけです。 この形式は、例でさらに使用されます。
loader.py
import struct import numpy as np import requests import gzip import pickle TRAIN_IMAGES_URL = "http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz" TRAIN_LABELS_URL = "http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz" TEST_IMAGES_URL = "http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz" TEST_LABELS_URL = "http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz" def downloader(url: str): response = requests.get(url, stream=True) if response.status_code != 200: print("Response for", url, "is", response.status_code) exit(1) print("Downloaded", int(response.headers.get('content-length', 0)), "bytes") decompressed = gzip.decompress(response.raw.read()) return decompressed def load_data(images_url: str, labels_url: str) -> (np.array, np.array): images_decompressed = downloader(images_url) # Big endian 4 unsigned int, 4 magic, size, rows, cols = struct.unpack(">IIII", images_decompressed[:16]) if magic != 2051: print("Wrong magic for", images_url, "Probably file corrupted") exit(2) image_data = np.array(np.frombuffer(images_decompressed[16:], dtype=np.dtype((np.ubyte, (rows * cols,)))) / 255, dtype=np.float32) labels_decompressed = downloader(labels_url) # Big endian 2 unsigned int, 4 magic, size = struct.unpack(">II", labels_decompressed[:8]) if magic != 2049: print("Wrong magic for", labels_url, "Probably file corrupted") exit(2) labels = np.frombuffer(labels_decompressed[8:], dtype=np.ubyte) return image_data, labels with open("test_images.pkl", "w+b") as output: pickle.dump(load_data(TEST_IMAGES_URL, TEST_LABELS_URL), output) with open("train_images.pkl", "w+b") as output: pickle.dump(load_data(TRAIN_IMAGES_URL, TRAIN_LABELS_URL), output)
線形回帰
線形回帰は、2つの変数間の関係を復元する方法です。 線形とは、変数が次の形式の方程式で表されると仮定することを意味します。
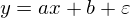ここのイプシロンはモデルの間違いです。 また、わかりやすく簡単にするために、1次元モデルを扱います。多次元性は複雑さを増しませんが、実例ではうまくいきません。 少しの間、MNISTを忘れて、一列に伸びるデータを生成します。 また、回帰モデル（仮説）を次のように書き直します。 
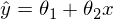。 帽子の付いたyは、モデルによって予測された値です。 
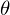1および2-不明なパラメーター-主なタスクはこれらのパラメーターを見つけることであり、xは自由変数であり、その値はわかっています。 問題をもう一度、わずかに異なる言語で定式化します-値のペアの形式で一連の実験データを取得します 
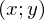そして、これらの値が位置する直線を見つける必要があります。実験データを最も一般化する直線を見つけます。 データを生成するための少しのコード：
generate_linear.py
import numpy as np import matplotlib.pyplot as plt TOTAL = 200 STEP = 0.25 def func(x): return 0.2 * x + 3 def generate_sample(total=TOTAL): x = 0 while x < total * STEP: yield func(x) + np.random.uniform(-1, 1) * np.random.uniform(2, 8) x += STEP X = np.arange(0, TOTAL * STEP, STEP) Y = np.array([y for y in generate_sample(TOTAL)]) Y_real = np.array([func(x) for x in X]) plt.plot(X, Y, 'bo') plt.plot(X, Y_real, 'g', linewidth=2.0) plt.show()
結果は次のようになります-準備されていない人間の目には十分にランダムです：
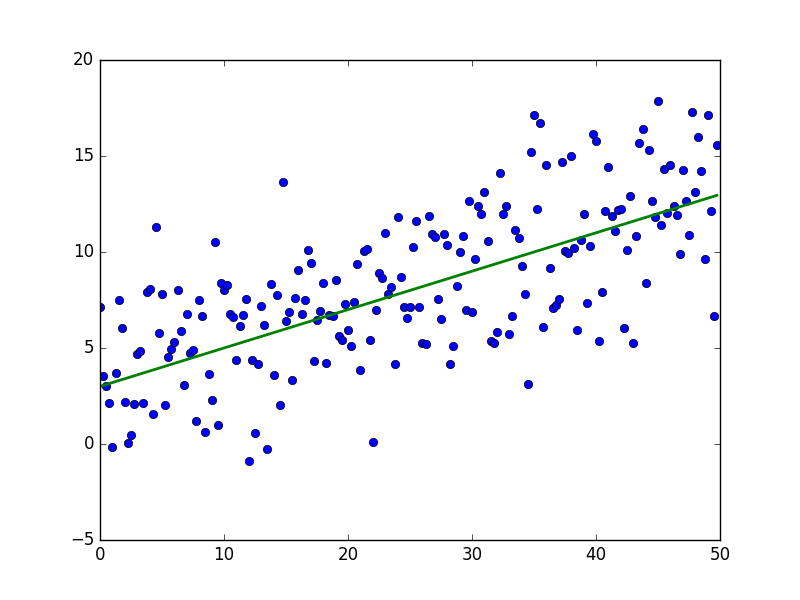
緑色の線は「ベース」です-データはこの線の上下にランダムに分布し、分布は均一です。 緑の線の方程式は次のとおりです。
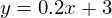
最小二乗法
MNCの本質は、そのようなパラメーターを見つけることです
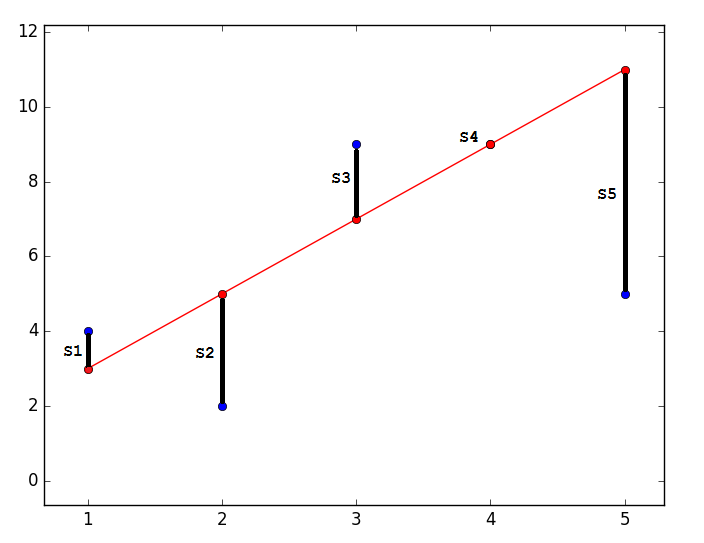
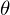予測値が実数に最も近いように。 グラフィカルに、何とかこのように表現されます：
コード
import matplotlib.pyplot as plt plt.plot([1, 2, 3, 4, 5], [4, 2, 9, 9, 5], 'bo') plt.plot([1, 2, 3, 4, 5], [3, 5, 7, 9, 11], '-ro') plt.show()
最も近い-は、ベクトル
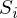可能な限り短い長さが必要です。 ベクトルは唯一のものではないため、すべてのベクトルの長さの2乗の合計は、パラメーターのベクトルが与えられたときに最小になる傾向があると仮定されます。 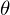。 私の意見では、かなり論理的な方法、投機的です。 それにもかかわらず、このRemarqueメソッドの正確さの数学的証明があります。長さはユークリッド距離を意味しますが 、これは必須ではありません。 備考2 ：平方の合計に注意してください。 繰り返しますが、長さの合計だけを最小化しようとすることを禁止する人はいません。 この図では、赤い点が予測値（ 
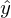）、青-実験の結果として得られた（帽子なしのy）。 
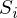-これはそれらの違い、ベクトルの長さです。
数学的には、次のようになります。
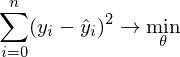-そのようなベクトルを見つけることが必要です 
式で 
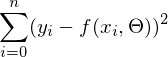最小に達する。 この式の関数fは次のとおりです。
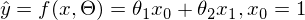または
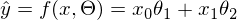
私は長い間、コードのベクトル化に直行する価値があるかどうかを考えました。その結果、それなしでは記事が長すぎます。 したがって、新しい表記法を導入します。
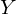従属変数yの値で構成されるベクトルです-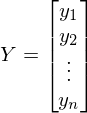 
-パラメータのベクトル- 
Aは、自由変数xの値の行列です。 この場合、最初の列は1（x_0がない）-
。 1次元の場合、行列Aには2列しかありません-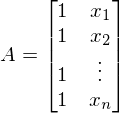 
新しい表記法の後、直線方程式は次の形式の行列方程式になります。
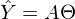。 この方程式では、2つの未知数が予測値とパラメーターです。 同じ方程式からパラメーターを見つけようとすることができますが、既知の値を使用します。 
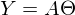それ以外の場合は、連立方程式として表すことができます。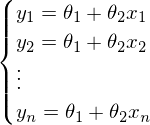 
ベクトルYとベクトルXの両方のすべてが既知であるように思えますが、方程式を解くためだけに残っています。 大きな問題は、システムに解決策がない場合があることです。そうでない場合、行列Aには逆行列がない場合があります。 解のないシステムの単純な例-同じ直線\平面\ハイパープレーン上にない3 \ 4 \ nポイント-これは、行列Aが非正方形になるという事実につながります。つまり、定義により逆行列はありません
。
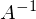「単純な方法」を解決できないことの良い例（ガウス法を使用してシステムを解決する）：
システムは次のようになります。
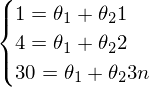-そのようなシステムの解決策を見つけることはまずありません。
その結果、これらの3つのポイントを通るラインを構築することは不可能です-ほぼ正しいソリューションしか構築できません。
そのような後退は、MNCとその兄弟がなぜ必要なのかの説明です。 コスト関数（損失関数）を最小限に抑え、絶対に正確なソリューションを見つけることができない（不要、有害）ことは、ニューラルネットワークの根底にある最も基本的なアイデアの一部です。 しかし、それらはまだ遠いですが、今のところ最小二乗法に戻りましょう。
最小二乗法は、次の形式のベクトルの二乗和の最小値を見つける必要があることを示しています。
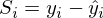すべてがベクトル\行列に変換されるとすると、平方の合計は次のように記述できます。 
。
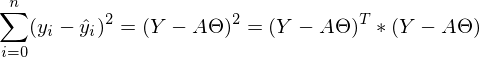私の言語はあえて些細な変換とは呼ばないでしょう。初心者が単純な変数からベクトルへと逃げるのは非常に難しいので、この式をすべて「オープン」ベクトルで完全に記述します。 繰り返しますが、単一の行が理解できない「魔法」ではないように。
まず、定義に従ってベクトルを「開き」ます。
。
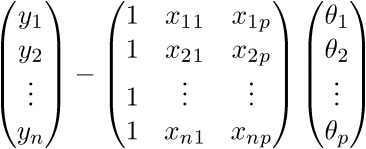次元を確認しましょう-行列Aの場合は（n; p）で、ベクトルの場合は
-（p; 1）、およびベクトル 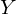-（n; 1）。 結果として、次元（n; 1）の2つのベクトルの差を取得します-
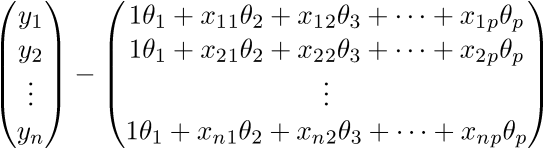
定義を見ます-定義により、右行列の各行は
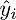。 さらに書きます：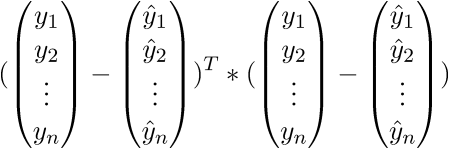 
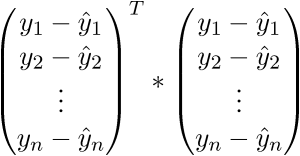
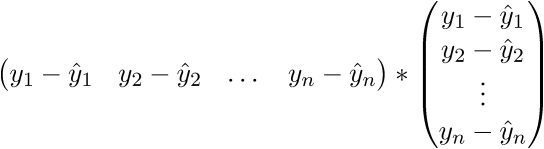
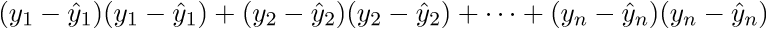
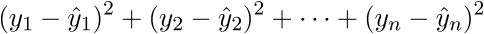
その結果、必要に応じて、最後の行は長さの2乗の合計になります。 もちろん、そのような心の中でのトリックは毎回かなり長い間変えることができますが、すぐにベクトル表記に慣れることができます。 これはプログラマにとってプラスになります。ベクトルがベクトル内を移動していたGPUに作業してコードを移植する方が便利です。 どういうわけか、Perlinノイズ生成をGPUに移植しました。ベクトル表記の概算を理解していたので、仕事はかなり良くなりました。 マイナスがあります-あなたは常に線形代数のアイデンティティとルールを覚えてインターネットを閲覧する必要があります。 ベクトル表記の信ac性を証明した後、さらに変換に進みます。
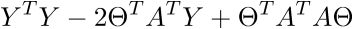
ここでは、行列の転置特性、つまり、和と積の転置が使用されます。 また、式が
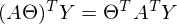そして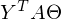 
定数があります。 定義から行列の次元を取得し、すべての乗算後に式の次元を計算することで証明できます。
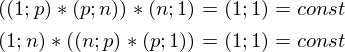
したがって、定数は対称行列として表すことができます。したがって、
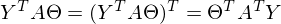
変換と括弧の開示の後、問題を解決する時が来ました-この式の最小値を見つけるために、与えられた
。 最小値は非常にカジュアルです-最初の微分を ゼロに。 良い方法では、まずこの最小値が存在することを証明する必要があります。証拠を省略し、 独立して文献を覗くことを提案します。 直観的に、したがって、関数が二次関数-放物線であり、最小値を持っていることは明らかです。
だから
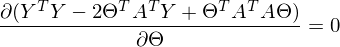
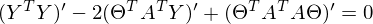
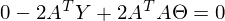
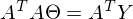
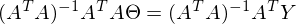
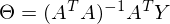
パート
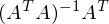疑似逆行列と呼ばれます。
これで、必要なすべての数式が利用可能になりました。 アクションのシーケンスは次のとおりです。
1）実験データのセットを生成します。
2）マトリックスAを作成します。
3）擬似逆行列を見つける
。
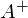4）検索
その後、問題は解決されます-実験データを最もよく要約する直線のパラメーターを自由に使用できます。 それ以外の場合、ある変数の別の変数への線形依存性を最もよく表す直線のパラメーターがあります。これはまさに必要なものです。
generate_linear.py
import numpy as np import matplotlib.pyplot as plt TOTAL = 200 STEP = 0.25 def func(x): return 0.2 * x + 3 def prediction(theta): return theta[0] + theta[1] * x def generate_sample(total=TOTAL): x = 0 while x < total * STEP: yield func(x) + np.random.uniform(-1, 1) * np.random.uniform(2, 8) x += STEP X = np.arange(0, TOTAL * STEP, STEP) Y = np.array([y for y in generate_sample(TOTAL)]) Y_real = np.array([func(x) for x in X]) A = np.empty((TOTAL, 2)) A[:, 0] = 1 A[:, 1] = X theta = np.linalg.pinv(A).dot(Y) print(theta) Y_prediction = A.dot(theta) error = np.abs(Y_real - Y_prediction) print("Error sum:", sum(error)) plt.plot(X, Y, 'bo') plt.plot(X, Y_real, 'g', linewidth=2.0) plt.plot(X, Y_prediction, 'r', linewidth=2.0) plt.show()
そして結果：
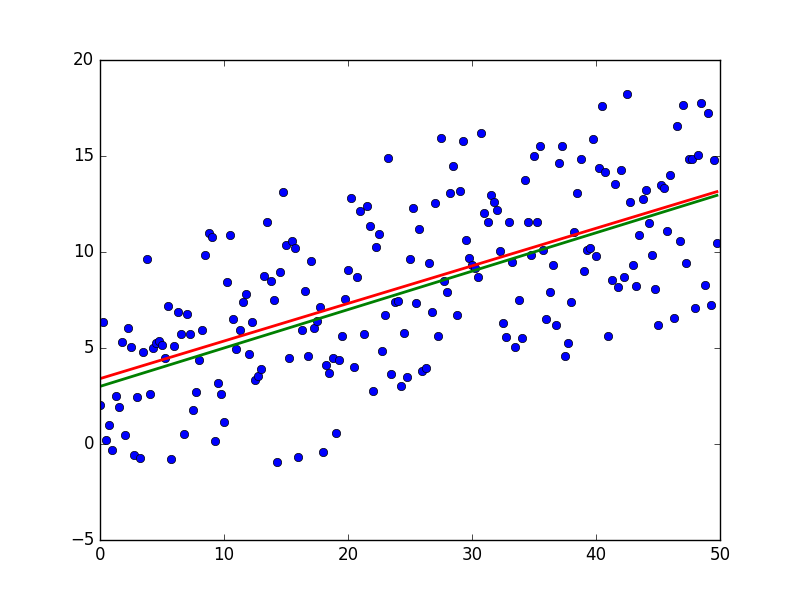
赤い線は予測されており、緑色の「ベース」とほぼ一致しています。 スタートアップのパラメーターは[3.40470411、0.19575733]です。 モデルエラーの分布はまだ不明であるため、値を予測しようとしても機能しません。 できることは、与えられたケースで最小二乗法が真であり、一般化に最適な方法であるかどうかを確認することです。 次の3つの条件があります 。
1）マットエラーの予想はゼロです。
2）エラーの分散は定数です。
3）異なる次元でエラーの相関はありません。 共分散はゼロです。
これを行うために、必要な値を計算してサンプルを補足し、2回測定を行いました。
generate_linear.py
import numpy as np import matplotlib.pyplot as plt TOTAL = 200 STEP = 0.25 def func(x): return 0.2 * x + 3 def prediction(theta): return theta[0] + theta[1] * x def generate_sample(total=TOTAL): x = 0 while x < total * STEP: yield func(x) + np.random.uniform(-1, 1) * np.random.uniform(2, 8) x += STEP X = np.arange(0, TOTAL * STEP, STEP) Y = np.array([y for y in generate_sample(TOTAL)]) Y_real = np.array([func(x) for x in X]) A = np.empty((TOTAL, 2)) A[:, 0] = 1 A[:, 1] = X theta = np.linalg.pinv(A).dot(Y) print(theta) Y_prediction = A.dot(theta) error = Y - Y_prediction error_squared = error ** 2 M = sum(error) / len(error) M_squared = M ** 2 D = sum([sq - M_squared for sq in error_squared]) / len(error) print("M:", M) print("D:", D) plt.plot(X, Y, 'bo') plt.plot(X, Y_real, 'g', linewidth=2.0) plt.plot(X, Y_prediction, 'r', linewidth=2.0) plt.show()
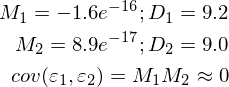
不完全ですが、すべてをごまかすことなく、期待どおりに機能します。
次の部分。
例を実行するライブラリの完全なリスト：numpy、matplotlib、requests。
記事で使用されている資料-https://github.com/m9psy/neural_nework_habr_guide