 最近、2〜3本の木を書く必要があり、ロシア語のインターネットで情報を探し始めました。 残念ながら、Habréやその他のリソースでロシア語で十分な情報を見つけることができませんでした。 すべてのリソースには同じものがありました。ツリーのプロパティ、キーがツリーに挿入される方法、ツリー内での検索、およびキーがツリーから削除される方法の簡単な例です。 実装はありませんでした。
最近、2〜3本の木を書く必要があり、ロシア語のインターネットで情報を探し始めました。 残念ながら、Habréやその他のリソースでロシア語で十分な情報を見つけることができませんでした。 すべてのリソースには同じものがありました。ツリーのプロパティ、キーがツリーに挿入される方法、ツリー内での検索、およびキーがツリーから削除される方法の簡単な例です。 実装はありませんでした。
したがって、必要なことを行った後、この記事を書くことにしました。 実際に彼らは通常2-3-treeと2-3-4-trees- 赤黒木に相当するものを認識するので、私はそれが教育目的のために誰かに役立つだろうと思います。
はじめに
バイナリ検索ツリーが何であるかとその欠点を知っている人は、さらにスクロールできます-ここでは新しいものはありません。
ほとんどのプログラマー(だけでなく)は、 二分探索木などのツリーを知っています 。 このツリーには非常に単純なプロパティがあります。
- 両方のサブツリー(左と右)はバイナリ検索ツリーです。
- 任意のノードXの左サブツリーのすべてのノードは、ノードX自体のデータキー値よりも小さいデータキー値を持ちます。
- (同じノードXの)右サブツリーのすべてのノードのデータキーの値は、ノードXのデータキーの値以上です。
検索ツリーは、検索操作を頻繁に実行する必要がある場合に使用されます。 通常の検索ツリーには非常に大きな欠点があります。ソートされたデータを入力として取得すると、ツリーは通常の配列になります。
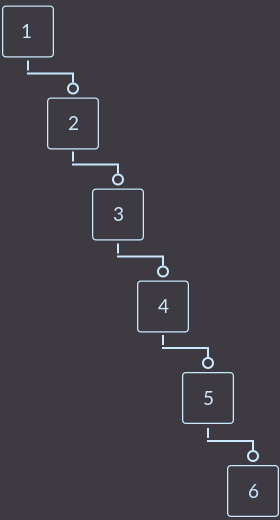
そして、 検索操作は配列と同じ複雑さで実行されます-O(n)の場合、nは配列内の要素の数です。
通常のツリーのバランスをとるには、いくつかの方法があります(検索の複雑度はO(log n)です)。 これは、nickme habrowserからの2つの記事で非常によく書かれています : ランダム化された検索ツリーとAVLツリー
2-3ツリーの一般的なプロパティ
ウィキからの定義:
2-3ツリーはデータ構造であり、次数1のBツリーです。ページには、2つの頂点(1つのフィールドと2つの子を持つ頂点)と3つの頂点(2つのフィールドと3つの子を持つ頂点)のみを含めることができます。 リーフトップは例外です。子はありません(ただし、1つまたは2つのフィールドがあります)。 2-3ツリーはバランスが取れています。つまり、左、右、および中央の各サブツリーの高さは同じであるため、等しい(またはほぼ等しい)データ量が含まれます。
プロパティ:
- 葉以外のすべての頂点には、1つのフィールドと2つのサブツリー、または2つのフィールドと3つのサブツリーが含まれます。
- すべての葉の頂点は同じレベル(下位レベル)にあり、1つまたは2つのフィールドが含まれています。
- すべてのデータがソートされます(バイナリ検索ツリーの原理に従って)。
- 葉以外の頂点には、サブツリーの値の範囲を示す1つまたは2つのフィールドが含まれます。 最初のフィールドの値は、左のサブツリーの最大値よりも厳密に大きく、右のサブツリー(3頂点の場合は中央のサブツリー)の最小値以下です。 同様に、2番目のフィールド(ある場合)の値は、中央サブツリーの最大値よりも厳密に大きく、右サブツリーの最小値以下です。 これらの非葉の頂点は、検索機能を目的のサブツリー、最終的には目的のシートに導くために使用されます。 ( 注同じキーがある場合、このプロパティは実行されません。したがって、左右のサブツリーに同じキーが同時に存在する可能性があり、非リーフ頂点のキーはこれらのキーと一致します。パフォーマンスアルゴリズム。 )。
2-3ツリーの例:
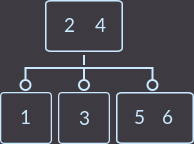
簡単にするために、異なるキーを使用します
コードでのツリーの表現
私自身はCプログラマーなので、いわゆる「C with classes」で記述しますが、コンストラクター、クラスメンバーメソッド、フレンドリ関数のようなC ++のものが本当に好きです。
ツリーの頂点は4つの頂点として表されます(これは、頂点が3つのキーと4つの息子を持つことができる場合です)。 このソリューションはいくつかの理由で選ばれました:第一に、素朴な(直接)実装を行うのが簡単であり、第二に、コードがifsによってフレーム化されているため、このソリューションにより、チェック回数を減らしてコードを簡素化することができました。
これが頂点ビューの外観です:
2-3ツリーの最上位のクラス
struct node { private: int size; // int key[3]; node *first; // *first <= key[0]; node *second; // key[0] <= *second < key[1]; node *third; // key[1] <= *third < key[2]; node *fourth; // kye[2] <= *fourth. node *parent; // , bool find(int k) { // true, k , false. for (int i = 0; i < size; ++i) if (key[i] == k) return true; return false; } void swap(int &x, int &y) { int r = x; x = y; y = r; } void sort2(int &x, int &y) { if (x > y) swap(x, y); } void sort3(int &x, int &y, int &z) { if (x > y) swap(x, y); if (x > z) swap(x, z); if (y > z) swap(y, z); } void sort() { // if (size == 1) return; if (size == 2) sort2(key[0], key[1]); if (size == 3) sort3(key[0], key[1], key[2]); } void insert_to_node(int k) { // k ( ) key[size] = k; size++; sort(); } void remove_from_node(int k) { // k ( ) if (size >= 1 && key[0] == k) { key[0] = key[1]; key[1] = key[2]; size--; } else if (size == 2 && key[1] == k) { key[1] = key[2]; size--; } } void become_node2(int k, node *first_, node *second_) { // 2-. key[0] = k; first = first_; second = second_; third = nullptr; fourth = nullptr; parent = nullptr; size = 1; } bool is_leaf() { // ; . return (first == nullptr) && (second == nullptr) && (third == nullptr); } public: // node(int k): size(1), key{k, 0, 0}, first(nullptr), second(nullptr), third(nullptr), fourth(nullptr), parent(nullptr) {} node (int k, node *first_, node *second_, node *third_, node *fourth_, node *parent_): size(1), key{k, 0, 0}, first(first_), second(second_), third(third_), fourth(fourth_), parent(parent_) {} friend node *split(node *item); // ; friend node *insert(node *p, int k); // ; friend node *search(node *p, int k); // ; friend node *search_min(node *p); // ; friend node *merge(node *leaf); // ; friend node *redistribute(node *leaf); // ; friend node *fix(node *leaf); // ( merge redistribute) friend node *remove(node *p, int k); // , ; };
挿入
キーキーを持つ要素をツリーに挿入するには、アルゴリズムに従う必要があります。
- ツリーが空の場合、新しい頂点を作成し、キーを挿入して、この頂点をルートとして返します。それ以外の場合は
- 頂点が葉である場合、キーをこの頂点に挿入し、頂点で3つのキーを取得する場合、それを分割します。
- キーキーを一番上の最初のキーと比較します。キーがこのキーよりも小さい場合は、最初のサブツリーに進み、それ以外の場合は手順2に進みます。
- 頂点に含まれるキーが1つだけである(2つの頂点である)場合は、右のサブツリーに進み、手順2に進みます。
- キーキーを上部の2番目のキーと比較します。キーが2番目のキーよりも小さい場合は、中央のサブツリーに進み、手順2に進みます。
- 適切なサブツリーに進み、ステップ2に進みます。
たとえば、キーの挿入= {1、2、3、4、5、6、7}:
key = 1を挿入すると、空のツリーが作成され、その後、単一のキー、key = 1を持つ単一の頂点が取得されます。

次に、キー= 2を挿入します。

ここで、キー= 3を挿入し、3つのキーを含む頂点を取得します。

この頂点は2-3ツリーのプロパティに違反するため、これに対処する必要があります。 ここでこの分割を処理します:中央にあるキー(この場合はキー= 2)、適切な場所に親頂点に転送します。または、ツリーに唯一の頂点がある場合は、ツリーのルートでもあります。新しい頂点を作成し、中間キーkey = 2をそこに転送し、残りのキーを並べ替えて、新しいルートの息子にします。
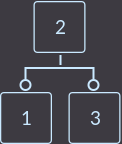
次に、アルゴリズムに従って、キー= 4を挿入します。

キー= 5:
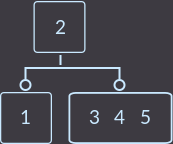
ここでも、2〜3本のツリーのプロパティが壊れていたため、分離を行います。
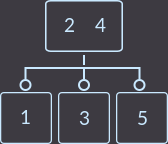
キー= 6:

キー= 7:
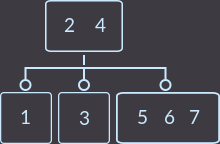
次に、2つの部門を作成する必要があります。 新しいキーが挿入される頂点には、3つのキーがあります(最初に分割します)。
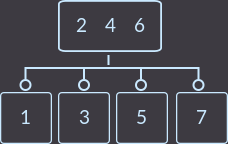
そして今、ルートには3つの頂点があります-それを分割してバランスの取れたツリーを取得します。通常のバイナリ検索ツリーを使用したこのような入力データでは、取得できませんでした:
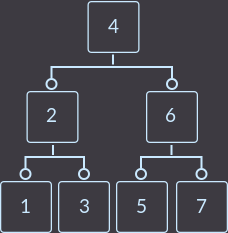
キー挿入
node *insert(node *p, int k) { // k p; , .. if (!p) return new node(k); // , 2-3- () if (p->is_leaf()) p->insert_to_node(k); else if (k <= p->key[0]) insert(p->first, k); else if ((p->size == 1) || ((p->size == 2) && k <= p->key[1])) insert(p->second, k); else insert(p->third, k); return split(p); }
頂点分割
node *split(node *item) { if (item->size < 3) return item; node *x = new node(item->key[0], item->first, item->second, nullptr, nullptr, item->parent); // , node *y = new node(item->key[2], item->third, item->fourth, nullptr, nullptr, item->parent); // , . if (x->first) x->first->parent = x; // "" "". if (x->second) x->second->parent = x; // , "" "" "", if (y->first) y->first->parent = y; // . if (y->second) y->second->parent = y; if (item->parent) { item->parent->insert_to_node(item->key[1]); if (item->parent->first == item) item->parent->first = nullptr; else if (item->parent->second == item) item->parent->second = nullptr; else if (item->parent->third == item) item->parent->third = nullptr; // . if (item->parent->first == nullptr) { item->parent->fourth = item->parent->third; item->parent->third = item->parent->second; item->parent->second = y; item->parent->first = x; } else if (item->parent->second == nullptr) { item->parent->fourth = item->parent->third; item->parent->third = y; item->parent->second = x; } else { item->parent->fourth = y; item->parent->third = x; } node *tmp = item->parent; delete item; return tmp; } else { x->parent = item; // , y->parent = item; // "" . item->become_node2(item->key[1], x, y); return item; } }
検索する
検索は、バイナリ検索ツリーと同じくらい簡単です。
- 現在の頂点でキーキーキーを探しています。見つかった場合は、頂点を返します
- キーが最初の頂点キーよりも小さい場合は、左のサブツリーに移動して、手順1に進みます。
- ツリー1にキーがある場合は、右のサブツリーに移動し(クラスにガイドされている場合は中央)、ステップ1に進みます。
- キーが2番目の頂点キーよりも小さい場合は、中央のサブツリーに進み、手順1に進みます。
- 適切なサブツリーに進み、ステップ1に進みます。
キー検索
node *search(node *p, int k) { // k 2-3 p. if (!p) return nullptr; if (p->find(k)) return p; else if (k < p->key[0]) return search(p->first, k); else if ((p->size == 2) && (k < p->key[1]) || (p->size == 1)) return search(p->second, k); else if (p->size == 2) return search(p->third, k); }
削除する
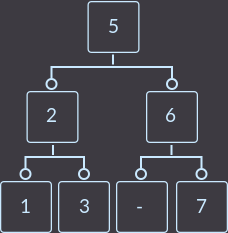
2-3ツリーでの削除は、他のツリーと同様に、リーフ(最下位の頂点)からのみ発生します。 したがって、削除するキーが見つかったら、まず、このキーがリーフまたは非リーフの頂点にあるかどうかを確認する必要があります。 キーがリーフ以外の頂点にある場合は、リーフの頂点から削除されたキーに対応するキーを見つけて、それらを交換する必要があります。 同等のキーを見つけるには、2つのオプションがあります。左側のサブツリーで最大要素を見つけるか、右側のサブツリーで最小要素を見つけるかのいずれかです。 2番目のオプションを選択しましょう。 例:

ツリーからキー= 4を削除するには、最初に同等のemu要素を見つけて交換する必要があります。キー= 3またはキー= 5です。 2番目の方法を選択したため、キーkey = 4とkey = 5を所定の場所で変更し、キー= 4をシートから削除します(ダッシュは削除したキーの場所を示します)。
最小キー検索
node *search_min(node *p) { // 2-3- p. if (!p) return p; if (!(p->first)) return p; else return search_min(p->first); }
キーの削除
node *remove(node *p, int k) { // k 2-3- p. node *item = search(p, k); // , k if (!item) return p; node *min = nullptr; if (item->key[0] == k) min = search_min(item->second); // else min = search_min(item->third); if (min) { // int &z = (k == item->key[0] ? item->key[0] : item->key[1]); item->swap(z, min->key[0]); item = min; // , .. min - } item->remove_from_node(k); // return fix(item); // . }
キーが削除された後、概念的に4つの異なる状況を取得できます。そのうちの3つはツリーのプロパティに違反し、1つは違反しません。 したがって、キーが削除された頂点に対して、fix()fix関数を呼び出す必要があります。これは、ツリーの2〜3個のプロパティを返します。 関数で説明されているケースについては、以下で説明します。
キーを削除した後のツリーの修正
node *fix(node *leaf) { if (leaf->size == 0 && leaf->parent == nullptr) { // 0, delete leaf; return nullptr; } if (leaf->size != 0) { // 1, , , if (leaf->parent) return fix(leaf->parent); else return leaf; } node *parent = leaf->parent; if (parent->first->size == 2 || parent->second->size == 2 || parent->size == 2) leaf = redistribute(leaf); // 2, else if (parent->size == 2 && parent->third->size == 2) leaf = redistribute(leaf); // else leaf = merge(leaf); // 3, return fix(leaf); }
次に、キーが削除された後に表示される可能性のあるオプションに移りましょう。 簡単にするために、ツリーの深さが2の場合を考えます。一般的な場合は、深さが3のツリーです。 その後、ツリー内のキーの削除をどのように深さで処理するかが明確になります。 ほとんどの状況の最後の例でこれを行います。 それまでの間、特別なケースに進みます。
ケース0:
次のケースだけでなく、最も単純なケースでも1つの文を理解するには十分です。ツリーが1つの頂点(ルート)で構成され、1つのキーがある場合、この頂点を削除します。 終わり。
事例1:
2つのキーが配置されているシートからキーを削除する必要がある場合は、キーを削除するだけで削除機能が終了します。
削除キー= 4:
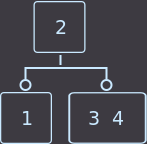 ->
-> 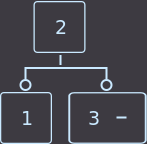 ->
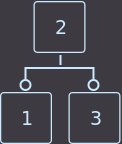
-> 
ケース2(配布または再配布 ):
キーを上部から削除すると、上部が空になります。 兄弟の少なくとも1人が2つのキーを持っている場合、単純な正しい配布を行い、作業は終了します。 正しい配布とは、親と息子の間でキーが周期的にシフトするため、親の孫も移動する必要があることを意味します。 任意の兄弟からキーを再配布できますが、最も便利なのは2つのキーを持つ隣人からです。たとえば、次の例のように、すべてのキーを循環的にシフトします。deletekey = 1
 ->
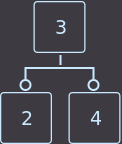
-> 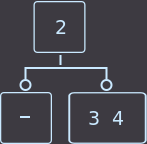 ->
-> 
または、2番目の例です。親には2つのキーがあり、それぞれ3人の息子がいます。キー= 4を削除します。 この例の再配布は、左兄弟と右兄弟の両方から実行できます。 左から選択しました:
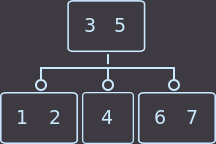 ->
-> 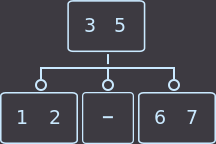 ->
-> 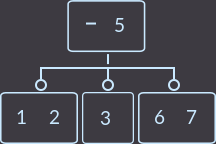 ->
-> 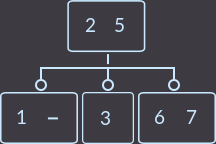 ->
->
->

ご覧のとおり、ツリーのプロパティが保存されます。
再配布
node *redistribute(node *leaf) { node *parent = leaf->parent; node *first = parent->first; node *second = parent->second; node *third = parent->third; if ((parent->size == 2) && (first->size < 2) && (second->size < 2) && (third->size < 2)) { if (first == leaf) { parent->first = parent->second; parent->second = parent->third; parent->third = nullptr; parent->first->insert_to_node(parent->key[0]); parent->first->third = parent->first->second; parent->first->second = parent->first->first; if (leaf->first != nullptr) parent->first->first = leaf->first; else if (leaf->second != nullptr) parent->first->first = leaf->second; if (parent->first->first != nullptr) parent->first->first->parent = parent->first; parent->remove_from_node(parent->key[0]); delete first; } else if (second == leaf) { first->insert_to_node(parent->key[0]); parent->remove_from_node(parent->key[0]); if (leaf->first != nullptr) first->third = leaf->first; else if (leaf->second != nullptr) first->third = leaf->second; if (first->third != nullptr) first->third->parent = first; parent->second = parent->third; parent->third = nullptr; delete second; } else if (third == leaf) { second->insert_to_node(parent->key[1]); parent->third = nullptr; parent->remove_from_node(parent->key[1]); if (leaf->first != nullptr) second->third = leaf->first; else if (leaf->second != nullptr) second->third = leaf->second; if (second->third != nullptr) second->third->parent = second; delete third; } } else if ((parent->size == 2) && ((first->size == 2) || (second->size == 2) || (third->size == 2))) { if (third == leaf) { if (leaf->first != nullptr) { leaf->second = leaf->first; leaf->first = nullptr; } leaf->insert_to_node(parent->key[1]); if (second->size == 2) { parent->key[1] = second->key[1]; second->remove_from_node(second->key[1]); leaf->first = second->third; second->third = nullptr; if (leaf->first != nullptr) leaf->first->parent = leaf; } else if (first->size == 2) { parent->key[1] = second->key[0]; leaf->first = second->second; second->second = second->first; if (leaf->first != nullptr) leaf->first->parent = leaf; second->key[0] = parent->key[0]; parent->key[0] = first->key[1]; first->remove_from_node(first->key[1]); second->first = first->third; if (second->first != nullptr) second->first->parent = second; first->third = nullptr; } } else if (second == leaf) { if (third->size == 2) { if (leaf->first == nullptr) { leaf->first = leaf->second; leaf->second = nullptr; } second->insert_to_node(parent->key[1]); parent->key[1] = third->key[0]; third->remove_from_node(third->key[0]); second->second = third->first; if (second->second != nullptr) second->second->parent = second; third->first = third->second; third->second = third->third; third->third = nullptr; } else if (first->size == 2) { if (leaf->second == nullptr) { leaf->second = leaf->first; leaf->first = nullptr; } second->insert_to_node(parent->key[0]); parent->key[0] = first->key[1]; first->remove_from_node(first->key[1]); second->first = first->third; if (second->first != nullptr) second->first->parent = second; first->third = nullptr; } } else if (first == leaf) { if (leaf->first == nullptr) { leaf->first = leaf->second; leaf->second = nullptr; } first->insert_to_node(parent->key[0]); if (second->size == 2) { parent->key[0] = second->key[0]; second->remove_from_node(second->key[0]); first->second = second->first; if (first->second != nullptr) first->second->parent = first; second->first = second->second; second->second = second->third; second->third = nullptr; } else if (third->size == 2) { parent->key[0] = second->key[0]; second->key[0] = parent->key[1]; parent->key[1] = third->key[0]; third->remove_from_node(third->key[0]); first->second = second->first; if (first->second != nullptr) first->second->parent = first; second->first = second->second; second->second = third->first; if (second->second != nullptr) second->second->parent = second; third->first = third->second; third->second = third->third; third->third = nullptr; } } } else if (parent->size == 1) { leaf->insert_to_node(parent->key[0]); if (first == leaf && second->size == 2) { parent->key[0] = second->key[0]; second->remove_from_node(second->key[0]); if (leaf->first == nullptr) leaf->first = leaf->second; leaf->second = second->first; second->first = second->second; second->second = second->third; second->third = nullptr; if (leaf->second != nullptr) leaf->second->parent = leaf; } else if (second == leaf && first->size == 2) { parent->key[0] = first->key[1]; first->remove_from_node(first->key[1]); if (leaf->second == nullptr) leaf->second = leaf->first; leaf->first = first->third; first->third = nullptr; if (leaf->first != nullptr) leaf->first->parent = leaf; } } return parent; }
ケース3(結合または結合 ):
おそらく最も困難なケースは、接着後は常にツリーを上に移動し、 マージ 操作または再配布操作を再度使用する必要があるためです。 再配布後、この操作の頂点は削除されないため、キーの削除後に2-3ツリーのプロパティを復元するアルゴリズムを停止できます。
まず、親が2人の息子(〜1キー)しか持たない頂点からkey = 3を削除する方法を見てみましょう。
 ->
->  ->
-> 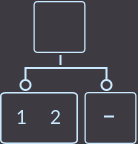 ->
-> 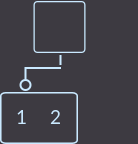 ->
-> 
私たちは何をしましたか? キーkey = 3を削除しました。 次に、キーを親からその息子がいる息子に転送する必要があります。この場合、左の息子に転送します。 次に、キーが削除された頂点を削除する必要があります。 最後の手順は、親がツリーのルートであるかどうかを確認し、このルートを削除して、キーを転送した頂点に新しい頂点を割り当てます。そうでない場合は、親のfix()修正関数を呼び出す必要があります。 簡単そうです。
次に、親に2つのキーがある場合、2つのオプションを検討します。 最初のオプションでは、削除キー= 3(中間息子から):
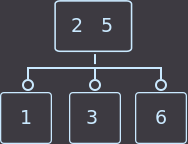 ->
-> 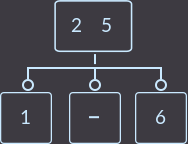 ->
-> 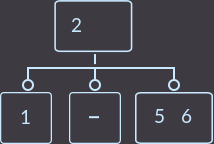 ->
-> 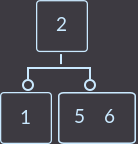
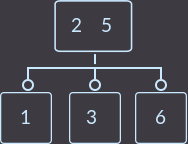
今回は何をしましたか? 親のキー(2つのうちの1つ)を息子に再度転送し、キーを持っていない息子を削除しました。 親には2つのキーがあるため、親がルートであるかどうかを確認する必要はありません。 上記の場合、修正アルゴリズムは次のとおりです。親の小さいキーを小さいキーを持つサブツリーに転送するか、大きいキーを大きいキーを持つサブツリーに転送し、キーのない頂点を削除する必要があります。 別の例、delete key = 1:
 ->
-> 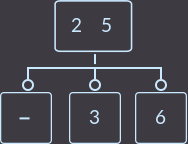 ->
-> 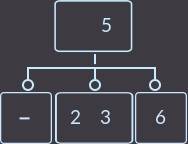 ->
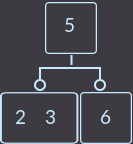
-> 
ボンディング
node *merge(node *leaf) { node *parent = leaf->parent; if (parent->first == leaf) { parent->second->insert_to_node(parent->key[0]); parent->second->third = parent->second->second; parent->second->second = parent->second->first; if (leaf->first != nullptr) parent->second->first = leaf->first; else if (leaf->second != nullptr) parent->second->first = leaf->second; if (parent->second->first != nullptr) parent->second->first->parent = parent->second; parent->remove_from_node(parent->key[0]); delete parent->first; parent->first = nullptr; } else if (parent->second == leaf) { parent->first->insert_to_node(parent->key[0]); if (leaf->first != nullptr) parent->first->third = leaf->first; else if (leaf->second != nullptr) parent->first->third = leaf->second; if (parent->first->third != nullptr) parent->first->third->parent = parent->first; parent->remove_from_node(parent->key[0]); delete parent->second; parent->second = nullptr; } if (parent->parent == nullptr) { node *tmp = nullptr; if (parent->first != nullptr) tmp = parent->first; else tmp = parent->second; tmp->parent = nullptr; delete parent; return tmp; } return parent; }
! 重要! 緑豊かなトップを接着または再配布する場合、兄弟の息子を接着および/または再配布する必要もあります。
キーを削除する最後の例:
すべての主要なケース( ケース0を除く)を表示できるような例を選択しました。 最初に、キーkeys = {10、20、30、40、50、60、70、80、90、100、110、120、130、140、150、5、15、25、8}を空のツリーに挿入して取得します:
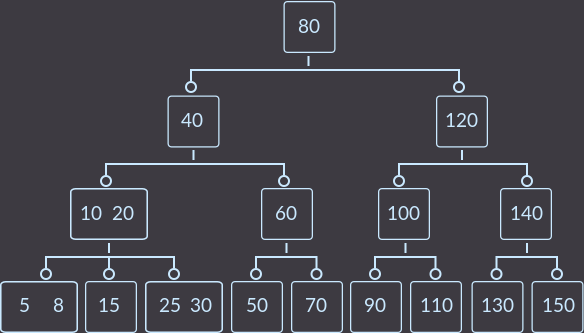
ここでキーを削除します。キー= {5、8、10、30、15}を順番に。
キーkey = 5を削除すると、次のようになります。
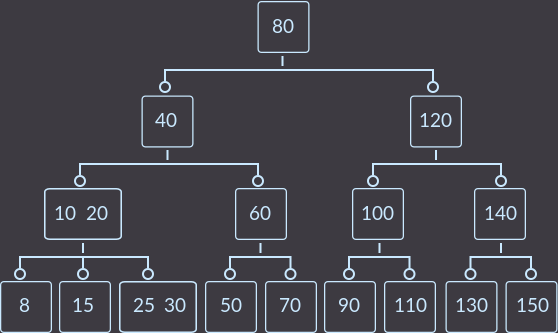
削除キー= 8:
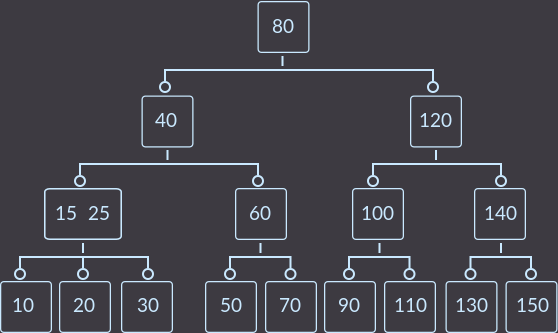
キー= 10:
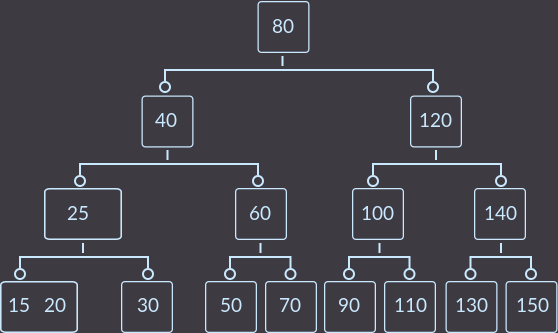
キー= 30:
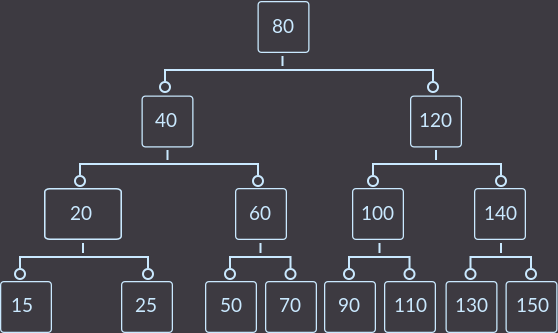
そして最後に、キー= 15。 ツリーの修正時にマージ操作が発生するため、すべての手順を見ていきます。
手順1.最初のfix()の呼び出し直後のツリーの表示:
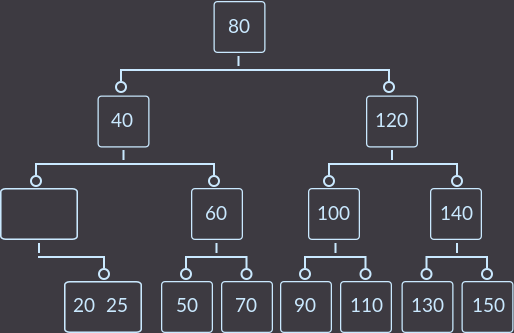
ステップ2.修正する2番目の呼び出し():
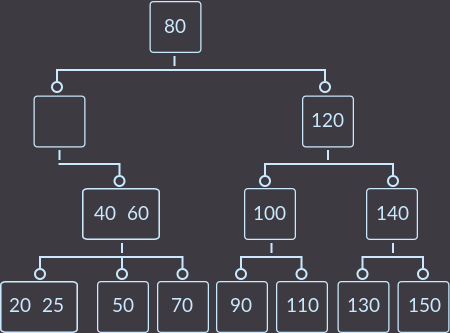
ステップ3.修正する3番目の呼び出し():
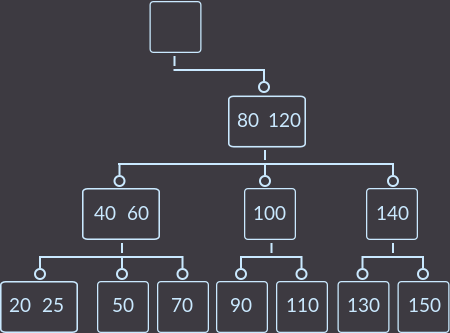
ステップ4.修正する最後の呼び出し():
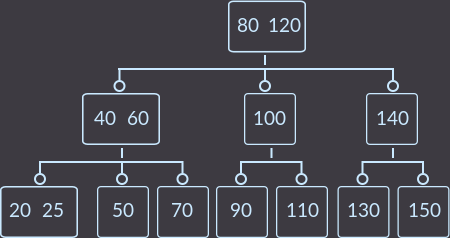
これは、キーkey = 15を削除した方法です。ツリーには、本来あるべきプロパティが残されています。
それだけです、ご清聴ありがとうございました。