♣️ 👨🏻‍🏭 🔏 インタビューでのドミノのタスク 👰 🙋🏽 🤶🏻

個人的な経験から、面のドミノをカバーすることに何らかの形で関連するタスクは、インタビューで非常に人気があると言えます。条件は異なる場合がありますが、すべての本質はそのままです。

例1

8 x 8セルのチェス盤があり、左下隅と右上隅が切り取られています。

このようなボードを2×1の正方形のドミノで完全に覆うことは可能ですか？

偶数個のセルがボード上に残っているため（62）、一見すると解決策が可能です。ただし、非常に簡単なことを1つ行います。

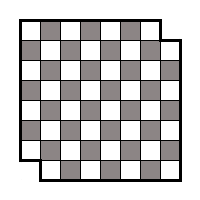
セルを1つで色付けしました。今、すべてが明らかになっています。各ドミノは、白と黒の2つのセルを厳密に占有できます。他のオプションはありません。ボード上のどのセルが切り取られているかを確認します。それぞれ黒で、32個の白いセルと30個の黒いセルがあり、そのようなボードを完全に覆うことはできません。

問題の条件はさまざまですが、一般的に、可能性と不可能性に関するタスクはすぐに明らかになります。

例2

27個の同一のチーズキューブとマウスキューブで構成される大きな3x3x3チーズキューブがあり、1つのキューブを食べると、その近くにあるチーズキューブ用に取られます。中央の立方体を食べられないダミーに置き換えた場合、マウスはすべてのチーズを完全に食べることができますか？

タスクは同じで、空間内のみであり、平面上ではありません。セルをカウントします。最初のシナリオでは、中央のキューブを削除した後の14 x 13です。14x 12であり、結果として解決策はありません。

次に人気のあるタスクは、ソリューションの数を数えることです。

例3

2つのボードが提供されます。

それぞれに2つのセルを切り取ります。ドミノをカバーするオプションの数はどれですか？どちらの場合も、異なる色のセルが切り取られたため、前の例の着色に関するすべての知識はここでは役に立ちません。タスクにインタビューする時間はあまりないので、何らかの手がかりを探す必要があります。しかし、彼女はそうです。最初のオプションから、2番目のボードの切り取りセルを含むすべてのコーティングを除外し、2番目のオプション-最初のオプションから除外します。（想像するのが非常に簡単な場合-切り取ったセルは最初はドミノで覆われていると仮定できます-ドミノは移動できません。明らかに、この方法でボードを同じ状態にし、コーティングオプションの数も同じになります）。その後、下隅の3 x 2セルを検討します。第２の実施形態では、左下のセルは一方向のみでコーティングすることができる。最初のボードのこのオプションを比較します。

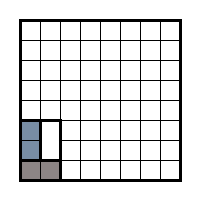
この角度を除いて、残りの部分はそれぞれ同一であり、コーティングの数も同一です。したがって、2番目のボードのコーティングバリアントごとに、1番目のボードのコーティングバリアントが比較されます。ただし、最初のケースでは、すべてのドミノが垂直に配置されているオプションも可能です。これは、2番目のボードのバリアントに対応していません。その結果、コーナーをカットしたセルでボードをカバーするオプションの数が増えました。

例4

ドミノコーティング2xNセルのオプションの数を見つけます。

X（N）メソッドでカバーされるようにします。左上のセルをカバーするオプションを検討してください。

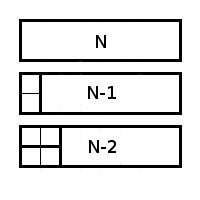
最初のケースの残りの部分はX（N-1）メソッドでカバーでき、2番目のケースでは明らかにX（N-2）メソッドでカバーできます。

すべてのカバレッジオプションがリストされ、どれも一致しないため、式X（N）= X（N-1）+ X（N-2）が得られます。

X（1）= 1、X（2）= 2、X（N）はフィボナッチ数列の数N + 1に等しくなります。

例5

3xNセルボードをドミノでカバーする方法の数を計算するプログラムを作成します。

この例には最適なソリューションもあるとすぐに言わなければなりませんが、ここでは特定のソリューションから一般的なソリューションに移行します。実際、このようなタスクの背後にあるものはすべて、 2部グラフで表すことができます。多くの頂点の1つは黒いセルで、もう1つは白いセルです。 Dominoのカバレッジは、このようなグラフの最大一致にすぎません。それを検索するには、さまざまなアルゴリズムを使用できます（たとえば、Kuhn）。オプションの数を計算すると、すべてが多少複雑になります。いずれにせよ、これはこの記事の範囲外です。

結論として、Pythonでの額アルゴリズムの実装を実証するために：

from itertools import combinations 
      

        
        
        
      

     #       
      

        
        
        
      

     #   
      

        
        
        
      

     # ,   2x2   : 
      

        
        
        
      

     # 1 2 
      

        
        
        
      

     # 3 4 
      

        
        
        
      

     # : 
      

        
        
        
      

     # mat = [ 
      

        
        
        
      

     # [0, 1, 1, 0], 
      

        
        
        
      

     # [0, 0, 0, 1], 
      

        
        
        
      

     # [0, 0, 0, 1], 
      

        
        
        
      

     # [0, 0, 0, 0] 
      

        
        
        
      

     #] 
      

        
        
        
      

     # 1 => 2, 1 => 3, 2 => 4, 3 => 4 
      

        
        
        
      

     #   ( . 3 => 1 ) 
      

        
        
        
      

     #      
      

        
        
        
      

     N = len(mat) 
      

        
        
        
      

     #       
      

        
        
        
      

     all_edges = combinations(xrange(N), 2) 
      

        
        
        
      

     #     
      

        
        
        
      

     edges = [(x,y) for x,y in all_edges if mat[x][y]] 
      

        
        
        
      

     #     
      

        
        
        
      

     matchings = [tuples for tuples in combinations(edges, N/2) \ 
      

        
        
        
      

     if len(set(reduce(lambda x, y: x+y, tuples))) == N] 
      

        
        
        
      

     print len(matchings) 
      

        
        
        
      

     # ,  O(N!)

インタビューでのドミノのタスク

例1

例2

例3

例4

例5

More articles: