最小化タスクは、各ユニットの最大カバレッジを見つけることであることを思い出させてください。 そのようなカバレッジが見つかり、それが一意である場合、それは機能のいわゆるコアに書き込まれ、それによってカバーされるすべてのユニットはさらなる検討から除外されます。 ただし、最大カバレッジが1つだけではない場合、追加の要件を考慮するためなどに使用できるソリューションオプションが発生します。 さらに、後で説明するように、オプションを破棄すると、結果のソリューションが最小限にならない可能性があるという事実につながります。
そのため、前の記事の例では、次の対称マップの関数のコアを見つけることができます。

次と等しい:
!X1 * X5 V X2 * X3 * X4 V X1 *!X2 *!X5
インデックス0の行とインデックス4の列の単位は、2つの方法でカバーできることがわかります。
!X1 * X3 *!X4(1)
X3 *!X4 *!X5(2)
同様に、インデックス10の行とインデックス4の列のユニットは、4つの方法でカバーできます。
!X1 * X3 *!X4(1)
X3 *!X4 *!X5(2)
!X1 * X2 * X3(3)
X2 * X3 *!X5(4)
異なるユニットをカバーする場合、同じ含意者が見つかることに注意してください。ここでは同じ番号で示されています。
さらに、インデックス30の行とインデックス4の列の単位は、次の3つの方法でカバーできます。
X3 *!X4 *!X5(2)
X1 * X3 *!X5(5)
X2 * X3 *!X5(4)
また、インデックス20の行のユニットとインデックス1の列は、次の2つの方法でカバーできます。
X1 *!X2 *!X3 *!X4(6)
!X2 *!X3 *!X4 * X5(7)
すべてのユニットは最終決定でカバーされる必要があるため、各ユニットのオプションの積として次の式を記述します。
(1 V 2)(1 V 2 V 3 V 4)(2 V 5 V 4)(6 V 7)
最初の2つのブラケットを明らかにします。
(1 * 1 V 1 * 2 V 1 * 3 V 1 * 4 V 2 * 1 V 2 * 2 V 2 * 3 V 2 * 4)(2 V 5 V 4)(6 V 7)
暗黙の値はそれ自体で乗算されるため、同じ暗黙の値を与えるため、最初の括弧は次の形式で書き換えることができます。
(1 V 1 * 2 V 1 * 3 V 1 * 4 V 2 * 1 V 2 V 2 * 3 V 2 * 4)(2 V 5 V 4)(6 V 7)
さらに、1つのimplicantを使用するオプションは2つのimplicantを使用するよりも優れたソリューションを提供するため、次の形式でソリューションを書き換えることができます。
(1 V 2)(2 V 5 V 4)(6 V 7)
さらに括弧を開き、同様の略語を使用すると、最終的な解決策が得られますが、これはもはや短縮できません。
2(6 V 7)
最初の要素2はグループ内の唯一の暗黙の要素であり、関数のコア(いわゆる拡張コア)に押し込む必要があります。
X3 *!X4 *!X5
ブラケットには2つのオプションがあります。
X1 *!X2 *!X3 *!X4
そして
!X2 *!X3 *!X4 * X5
いずれかを選択できます。
当然、このアルゴリズムの自動化に関して疑問が生じます。 これを行うために、apssymmapプログラムを作成しました。これは私のWebサイトで見つけることができます。
http://andyplekhanov.narod.ru/soft/soft.htm
この方法を適用した結果を他の既知の方法と比較することは興味深いことです。 以下の例を使用して、apssymmapプログラムの結果をよく知られているエスプレッソプログラムと比較します。
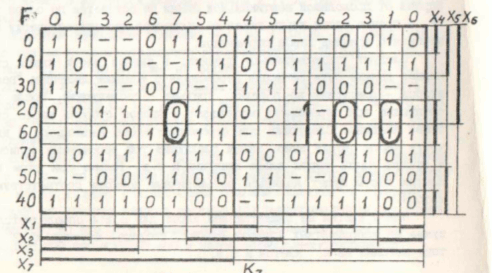
エスプレッソプログラムの結果:
espresso -Dexact -oeqntott test.txt

apssymmapプログラムの結果:

apssymmapプログラムは、エスプレッソ用ではなく8つの異なるオプションを生成することがわかります。 しかし、より興味深い事実は、エスプレッソの結果が最適ではないということです。 これらのソリューションの共通部分をすべて破棄すると、エスプレッソには2つのインプラントが残っていることがわかります。
!X7 *!X5 *!X4 * X2 * X1
そして
X7 *!X6 * X5 * X4 * X3 * X1
それぞれ5個と6個の変数を含み、apssymmapソリューションには暗黙の要素があります
!X5 * X3 * X2 * X1
そして
X7 *!X6 * X3 * X2 * X1
4つと5つの変数を含む、つまり2つ少ない。 結論として、対称カードはブール関数を手動で最小化するためのより便利な方法であるだけでなく、コンピューターでこの問題を解決する他の方法を凌ぐと結論付けることができます。