👆🏾 🦗 🐺 ベイジアンニューラルネットワーク-今オレンジ（パート2） ☘️ 🤚🏿 🐬

オレンジにもっとあると思います-皮、またはうーん、オレンジ？

可能であれば、キッチンに行き、オレンジを取り、皮をむいて確認することをお勧めします。怠か手元にない場合-私たちは退屈な数学を使用します：私たちは学校からのボールの量を覚えています。皮の厚さが等しいとしましょう

半径から

、

; 一方から他方を引き、皮の体積をオレンジの体積で割ると...皮が約16％であることがわかります。ちなみに、それほどではありません。

1000次元の空間にあるオレンジはどうですか？

今回はキッチンに行きますが動作しません。誰もが式を暗記しているわけではないと思うが、ウィキペディアは私たちを助けてくれる。同様の計算を繰り返しますが、興味深いことに次のことがわかります。

まず、1000次元のハイパーエペリンは果肉よりも皮をむく
第二に、約246993291800602563115535632700000000000000倍です

つまり、いかに奇妙で矛盾しているように見えても、ハイパーエペルシンのほぼ全体が、その表面のすぐ下のごくわずかな薄い層に含まれています。

おそらくこれから始めましょう。

あらすじ

これは、ポストの 2番目の部分であり、その前に、メイングラール（モデルパラメーターの事後確率）を見つけることに焦点を当てていました。念のため、ここにあります。

。もう一度思い出してください

モデルパラメーター（たとえば、ニューラルネットワークの重み）、および

-データセットからのデータ（表記を少し変更し、代わりに以前の

だった

しかし、後でシータが必要です）。

だから、オレンジはそれだけです。この後部の寸法は、ハイパーエペルシンの量と同じ驚くべき速度で成長しています。パラメータが多いほど、分布は「大きく」なります。実際には、オレンジでさえ想像しない方が良いでしょう。山を想像してみましょう。千次元で。はい、私はこれが少し矛盾していることを知っていますが、ここでは山があります：

これは本当に一次元です。 ヒントンの証言によると、このような千次元の山を想像することができます。上の写真を見て、「千！」と言ってください-またはいくつ必要になるでしょうか

私たちの課題は、この山の体積を調べることです。そうすることで、我々は：

-私たちはそれがどんな形なのかわかりません（たぶん）

-（今のところ）測定方法は1つだけです-ある地点に立って、足までの高さを計算できます（この地点にいる確率）

-山の表面は、成長すると指数関数的に成長します

-ハイパーエペルシンの皮膚が成長する方法と同様

計画は何ですか？

計画1：サンプリング

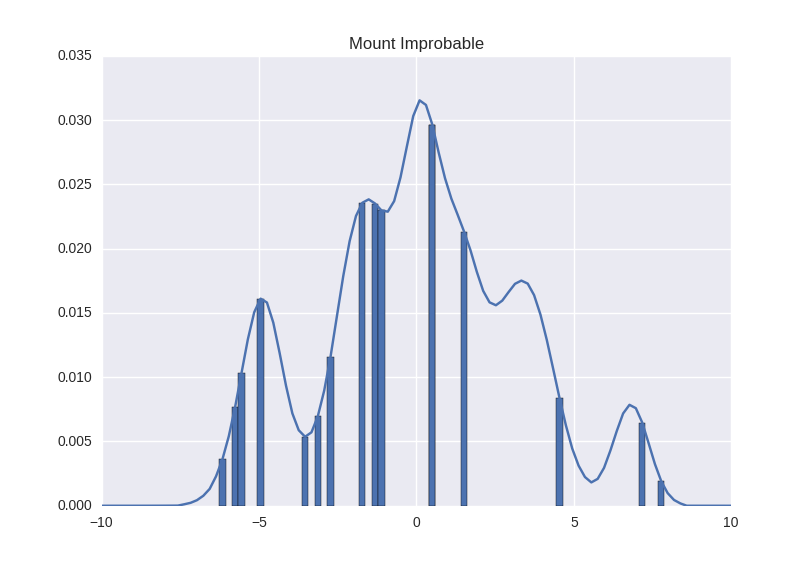
一般的に、各ポイントで直接山を測定する必要はありません。山のいくつかのランダムなセクションを選択し、測定を行い、その結果の概要を説明できます。それはそれほど正確ではありませんが、より少ない測定を行う必要があります。

これは、それ自体が懇願する思考であることにすぐに気付くことができますが、多次元の山が次元数の増加とともに成長し始めたとき、それはあまり役に立ちません。山の表面は、<次元の数>の程度の<1つの次元の値の数>に等しいことを思い出してください。サンプリングは次数の基礎を減らすのに役立ちますが、指数はどこにも行かず、問題は指数関数のままです。

計画2：近似

山を測定する主な問題は、山が大きいことではありません（測定回数の点で）-最後に、Wikipediaの式に従って、1000次元のオレンジのボリュームをそれほど困難なく計算しました。問題は、山の公式がないことです 。山が成長する分析規則はわかりません（オレンジとは異なり、すべての方向に均等に成長します）。

さて、私たちが探しているものに似ているが、今度は式を使用して、独自の別の山を構築するとどうなりますか？このようなもの：

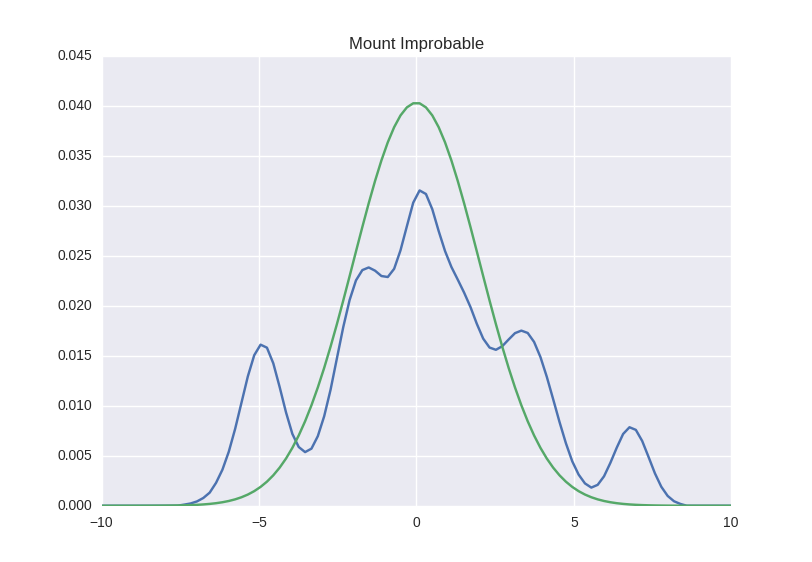
まあ...実際に悪魔は彼を知っています。第一に、それはまだあまり明確ではなく、近似は非常に正確である可能性があります-写真ではあまり良く見えません。第二に、これを行う方法がまだわかりません。さあ、始めましょう。

ラプラス近似

もう一度、ベイズの定理を少しだけ異なる方法で描きます。

分数の右側にある2つの確率の積を1つにまとめました。いわゆる結合確率（そして、もう一度、表記をシータではなくwにわずかに変更したことを思い出します）。人々はしばしばこれを次の意味で見る

-「望ましい」配布、および

結果を1に合計するために必要な正規化定数です。一時的に検索に集中しましょう

。

テイラー級数を思い出してください。解析の最初のコースに従って、任意の関数が無限量の定義された多項式に分解されます。関数を書く

どうやって

、そして私たちはある時点でレイアウトします

、これは最大分布と一致します（どこにあるかはわかりませんが、これはまだ重要ではありません）。同時に、用語の後に2のべき乗で無限の量を切り捨てます。

（これは、Wikipediaからの1対1の直接的な廃止されたテイラー拡張です）

今、私たちが選んだことを覚えておいてください

最大点として、それはその中の微分がゼロに等しいことを意味します。つまり、2番目の用語は明確な良心をもって捨てることができます。取得します

何にも似ていませんか？実際、このことはガウスの対数と同じ形をしています。これを見るために、あなたは書くことができます

表記を少し変更してみましょう。

そして今それをさせます

。それから

、そして、所望の結合確率は、最大点と標準偏差に中心があるガウスによって近似できることがわかります

（最大点または曲率での逆二次導関数）。

1つのセクションにあいまいな文字が多すぎる場合は、3つの短いパラグラフでアイデアを要約します。したがって、山のボリュームを検索する場合は、次のものが必要です。

-最大ポイントを見つける

-その中の曲率を測定します（二次導関数を計算します;唯一の注意：に関する微分

しかしではない

）

-最大点と標準偏差を中心とする法線曲線を取ります-曲率に負の反比例。

山のピークポイントを検索することができ、すべてを測定するよりもはるかに簡単です。実際、前回の投稿でごちゃごちゃにしたのと同じベイジアン回帰に魔法をかけましょう！

最後の投稿の最後で最大点を検索しました-これは、ベイジアンバンドルの中心、「最もホットな線」などです。念のため、もう一度見つける方法を説明しますが、フォーミュラで人々を怖がらせないように、スポイラーの下に隠します。

ネタバレ見出し

ここで、argmaxの下の最初の部分は尤度であり、2番目はガウス事前分布です。製品は、通常のように対数をとって量に変換されました。

の誘導体

分析的に数えることができますが、私はひどいカウチポテトなので、私はそれをすべてPythonに入れて、aurogradに私のために仕事をさせたいです。

# b  w       ,      #       ext_w = np.hstack([b, w]) #      #     ,  ext_data.dot(ext_w) #  data.dot(w) + b ext_data = np.ones((data.shape[0], data.shape[1] + 1)) ext_data[:, 1:] = data #   log joint,      #        def log_joint(w): regression_value = ext_data.dot(w) return ( np.sum(-np.power(target - regression_value, 2.) / (2 * np.power(1., 2.))) + np.sum(-np.power(w, 2.) / (2 * np.power(1., 2.))) ) from autograd import elementwise_grad second_grad_log_joint = elementwise_grad(elementwise_grad(log_joint)) mu = ext_w sigma = -1. / second_grad_log_joint(ext_w) cov = np.diag(sigma) # ,      # some_value = multivariate_normal.pdf(some_point, mu, cov)...

ディストリビューションがある場合、それを描くことは技術的な問題です。ポストの最後の部分とほぼ同じ方法を少し変更して使用します（中心からの距離が異なるサンプル分布）。こんな素敵な写真が得られます：

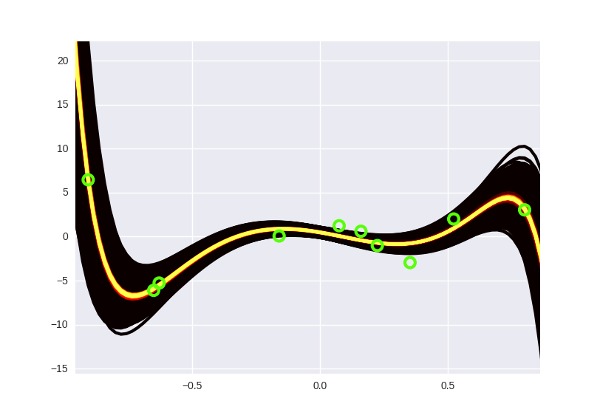
ところで、ここのすべての曲線は15次の多項式です。昔の「強引な」ベイジアン回帰は、数年前からコンピューター時代に戻っていました（どういうわけか、5度を絞りました）。

ラプラス近似はすべての人に適しています-高速、便利、美しい-しかし、1つ悪い点があります。それは最大点で推定されます。それは山全体で判断するようなもので、頂上から見たものです-本当に頂上にいるのか、それとも局所的な最大値に留まっているのかわからないという事実と、そこからすべてが見えるわけではないという事実にもかかわらず（突然、すべてが非常に平らで美しい、その下に3キロメートルの断崖絶壁がありますか？）一般に、彼らはニューラルネットワークのためにそれを思いついた、あなたが推測するかもしれない、ラプラスの時ではなく、1991年でさえ、それ以来、それは実際に世界に勝っていない。それでは、もっとファッショナブルで美しいものを見てみましょう。

backpropによるベイズ：開始

最後に、DeepMindのタイトル記事からまさにその方法に到達しました。著者は、backpropでBayesと呼んでいます-ロシア語への翻訳で幸運を祈ります。逆ベイズ伝搬？

ここからの出発点はこれです。ある種の近似があると想像してください

（これはシータ記号が便利な場所です-これらは近似分布パラメータになります）、それを何らかの単純な形式、たとえばガウス型にします。秘trickは次のとおりです。元の山の近似値からの「距離」の表現を書き留め、この距離を最小化します。両方の量が確率分布であるため、分布を比較するために特別に考案されたものを結合します：カルバック・ライブラー距離。実際、少し怖いように聞こえますが、これだけです：

積分を注意深く見ると、それが期待のように見えることが明らかになります-積分の下には、ある種のものがあり、

、そして積分が引き継がれます

。その後、次のように記述できます。

さらに進んでください：分母に

、そして、ベイズの定理により、

。上記の式に入れて、期待の下にあることに注意してください

-に依存しない

、そして私たちはそれを期待から外すことができます：

これはとてもクールなことでした。あなたが忘れていないなら、この全体は近似値と私たちの山の差に等しいからです。ここで管理されるパラメーターは

、そして差が最小になるように調整したいと思います。したがって、この最小化のプロセスでは、心配する必要はありません。

-それはに依存しないため

。ちなみに、これは後部の主な問題要素でした-計算するためには、山のすべてのポイントを回って、それらをまとめる必要がありました（なぜなら

、すべての量

、他の方法で入手することはできません）。

しかし、先に進みます。残っているものの最小値を見つけることに関心があります。

通常、どのように低値を探しますか？さて、導関数を取り、勾配降下を行います。このゴミから派生物を取得する方法はありますか？今のところあまり良くないことがあります。

backpropによるベイズ：続き

ここに私が直感的に入力することができなかった部分が来るので、歯を磨いて数学に従う必要があります。導関数を取得できる部分は、再パラメーター化トリックと呼ばれ、次の手順で構成されます。

ランダム変数を取ったとしましょう。彼女については何も知らない。これが彼女の財産であり、これまでのところ彼女に関するすべてです。
一般的に言えば、期待の導関数は見かけほどひどいものではありません。それは単に積分の導関数、つまり大まかに言って、合計が終わった合計の導関数です。それ自体は恐ろしくありませんが、退屈です。「無限に成長するすべてのポイントをまとめる」という問題に再び戻るからです。「。一般的な用語で、期待の下で何らかの機能を想像してみましょう、デリバティブを記述します。

私たちは特別なことは何もしませんでした-ウィキペディアからの定義によって期待を開き、それを不可欠なものとして再び書き留めました。でもね

最後に？私たちはちょうどそれが等しいと言った

。そして...

今、積分はイプシロン上で行われます。つまり、微分を

積分の符号の下で。

ここに、再パラメータ化のトリックがあります。期待の導関数があり、それが導関数の期待になりました。かっこいいもしあなたがまだゆっくりと私の指のガイドに従っているなら、あなたはあまりクールではなく、おそらく何が変わったのかさえ明確ではないでしょう-私たちは1つのFIGを統合する必要があります

私たちは何を達成しましたか？

一番下の行は、いくつかの点（サンプル）でこの積分を近似できることです。そして、彼らができなかった前に。以前は、デリバティブは全額から取得する必要がありました。まず、一連のポイントをまとめてから、それを区別します。コレクション内の不正確さは、差別化する際に、はるかに間違った方向に私たちを導く可能性があります。そして今、私たちは点で区別し、結果を要約することができます-したがって、部分的な合計でかなりできます。

近似推論の世界におけるこのような厳しい順序は次のとおりです。ここでは、事後分布自体でなく、 導関数を計算するための近似が必要です。まあ、何も、私たちはほとんどそこにあります。

backpropによるベイズ：アルゴリズム

これまでのところ、私たちはに属している

抽象的な「パラメータ」として：それらを明確にする時が来ました。近似させて

ガウスになります：そして想像してください

形で

-平均値、および

-標準偏差。また、決定する必要があります

-ゼロと標準偏差1を中心とするガウス確率変数にしましょう。

。次に、再パラメーター化の条件が満たされるように、

（

ここでは、要素ごとの乗算を意味します）。しかし、私にとっては、なぜ同時に

（もし誰かが自分の指のコメントで説明できるなら-私は非常に感謝します）、しかし私たちは信仰に関する記事のこの部分を取ります。

全体として、逆分布は次の手順で構成されます。

ランダムで開始そして各ニューラルネットワークの重み（または回帰係数）
少しサンプルから
私たちはそれから得る
「真の山」と近似間の距離の関数を思い出します。かつてしかし、良い意味でそれ。とにかく下に書きます、それは簡単です（覚えておいてください）
についての微分を考慮する。次のようになります。

（プラスはどこですか？ 2つの変数の関数であり、両方が依存します）
についての微分を考慮する：
派生物があります-それは比hat的に帽子をかぶっています。さらに古き良き勾配降下法：

すべての結果

あなたのことは知りませんが、この黒と黄色のビームにはもううんざりしているので、この必須の段階をスキップして、ニューラルネットワークのようなことをしましょう。元の記事の著者は、畳み込みネットワークを使用するなどの追加の歪みなしに、MNIST数字で素晴らしい結果を得ました-それらに到達してみましょう。そしておそらく、かなりの自動卒業生を脇に置き、テアノのようなもっと重いもので武装する時が来たのでしょう。その後、Theano固有のコードが少しあるので、それをナビゲートしない場合は、自由にめくります。

データを取得します。

 from sklearn.datasets import fetch_mldata from sklearn.cross_validation import train_test_split from sklearn import preprocessing import numpy as np mnist = fetch_mldata('MNIST original') N = 5000 data = np.float32(mnist.data[:]) / 255. idx = np.random.choice(data.shape[0], N) data = data[idx] target = np.int32(mnist.target[idx]).reshape(N, 1) train_idx, test_idx = train_test_split(np.array(range(N)), test_size=0.05) train_data, test_data = data[train_idx], data[test_idx] train_target, test_target = target[train_idx], target[test_idx] train_target = np.float32(preprocessing.OneHotEncoder(sparse=False).fit_transform(train_target))

パラメーターを宣言します。ここでは、記事に記載されている小さなトリックを適用しますが、私は故意に伝えませんでした。問題はこれです。各ネットワークの重みに対して、muとsigmaの2つのパラメーターがあります。 sigmaは常にゼロよりも大きくなければならないという事実で、小さな問題が発生する場合があります（これはガウスの標準偏差であり、定義によって負になることはできません）。まず、どのように初期化するのですか？さて、0に非常に近い値（0.0001など）から1までの乱数を使用できます。第二に、ゼロ以下の勾配降下中に停止しませんか？おそらく、そうすべきではありませんが、あらゆる種類の算術的な不正確さのために、小数点はそうかもしれません。一般的に、著者はこれをエレガントに解決することを提案しました-シグマをシグマの対数に置き換え、重みの公式を適切に修正します：

（なぜここで+1対数の下にあるのでしょうか？明らかに、同じ目的で-誤って対数をゼロから取らないように）。

ああ、まあ、私たちはいつもスケールについて話しました

しかし、ニューラルネットワークでは、多くの場合、独自の命名法-ゼロウェイト、

そこに呼ばれた

（バイアス）。私たちは契約に違反しません。だから：

 def init(shape): return np.asarray( np.random.normal(0, 0.05, size=shape), dtype=theano.config.floatX ) n_input = train_data.shape[1] # L1 n_hidden_1 = 200 W1_mu = theano.shared(value=init((n_input, n_hidden_1))) W1_logsigma = theano.shared(value=init((n_input, n_hidden_1))) b1_mu = theano.shared(value=init((n_hidden_1,))) b1_logsigma = theano.shared(value=init((n_hidden_1,))) # L2 n_hidden_2 = 200 W2_mu = theano.shared(value=init((n_hidden_1, n_hidden_2))) W2_logsigma = theano.shared(value=init((n_hidden_1, n_hidden_2))) b2_mu = theano.shared(value=init((n_hidden_2,))) b2_logsigma = theano.shared(value=init((n_hidden_2,))) # L3 n_output = 10 W3_mu = theano.shared(value=init((n_hidden_2, n_output))) W3_logsigma = theano.shared(value=init((n_hidden_2, n_output))) b3_mu = theano.shared(value=init((n_output,))) b3_logsigma = theano.shared(value=init((n_output,)))

このログシグマは、どういうわけか正規分布式にプッシュできる必要があるため、独自の関数を作成します。同時に、通常のものを宣言します：

 def log_gaussian(x, mu, sigma): return -0.5 * np.log(2 * np.pi) - T.log(T.abs_(sigma)) - (x - mu) ** 2 / (2 * sigma ** 2) def log_gaussian_logsigma(x, mu, logsigma): return -0.5 * np.log(2 * np.pi) - logsigma / 2. - (x - mu) ** 2 / (2. * T.exp(logsigma))

確率を評価するときです。以前に収集したように、サンプリングによってこれを行います。つまり、ループでスピンし、反復ごとにランダムに初期化するイプシロンを取得し、それを重みに変換して組み合わせます。一般に、Theanoにはループのスキャンがありますが、1）ユーザーの脳を可能な限り破壊することを目的に、man探究者のチームによって明確に開発されました。2）少数の反復で、通常のループが機能します。合計：

 n_samples = 10 log_pw, log_qw, log_likelihood = 0., 0., 0. for _ in xrange(n_samples): epsilon_w1 = get_random((n_input, n_hidden_1), avg=0., std=sigma_prior) epsilon_b1 = get_random((n_hidden_1,), avg=0., std=sigma_prior) W1 = W1_mu + T.log(1. + T.exp(W1_logsigma)) * epsilon_w1 b1 = b1_mu + T.log(1. + T.exp(b1_logsigma)) * epsilon_b1 epsilon_w2 = get_random((n_hidden_1, n_hidden_2), avg=0., std=sigma_prior) epsilon_b2 = get_random((n_hidden_2,), avg=0., std=sigma_prior) W2 = W2_mu + T.log(1. + T.exp(W2_logsigma)) * epsilon_w2 b2 = b2_mu + T.log(1. + T.exp(b2_logsigma)) * epsilon_b2 epsilon_w3 = get_random((n_hidden_2, n_output), avg=0., std=sigma_prior) epsilon_b3 = get_random((n_output,), avg=0., std=sigma_prior) W3 = W3_mu + T.log(1. + T.exp(W3_logsigma)) * epsilon_w3 b3 = b3_mu + T.log(1. + T.exp(b3_logsigma)) * epsilon_b3 a1 = nonlinearity(T.dot(x, W1) + b1) a2 = nonlinearity(T.dot(a1, W2) + b2) h = T.nnet.softmax(nonlinearity(T.dot(a2, W3) + b3)) sample_log_pw, sample_log_qw, sample_log_likelihood = 0., 0., 0. for W, b, W_mu, W_logsigma, b_mu, b_logsigma in [(W1, b1, W1_mu, W1_logsigma, b1_mu, b1_logsigma), (W2, b2, W2_mu, W2_logsigma, b2_mu, b2_logsigma), (W3, b3, W3_mu, W3_logsigma, b3_mu, b3_logsigma)]: # first weight prior log_pw += log_gaussian(W, 0., sigma_prior).sum() log_pw += log_gaussian(b, 0., sigma_prior).sum() # then approximation log_qw += log_gaussian_logsigma(W, W_mu, W_logsigma * 2).sum() log_qw += log_gaussian_logsigma(b, b_mu, b_logsigma * 2).sum() # then the likelihood log_likelihood += log_gaussian(y, h, sigma_prior).sum() log_qw /= n_samples log_pw /= n_samples log_likelihood /= n_samples

ふう。今、私たちは目的を集めます。記事のこの場所のどこかで2週間休止する必要があります。これは、記事で提案されている目標(log_qw - log_pw - log_likelihood / M).sum()

ようなもの）が機能しなかったため、悪い結果。それからある時点で、私はこの記事を最後まで読むことにし、著者はミニバッチを使って特定の方法で目標を平均化することを勧めていることに気付きました。より正確には、このようにでも：

 objective = ((1. / n_batches) * (log_qw - log_pw) - log_likelihood).sum() / batch_size

同時に、彼らは通常の勾配降下の代わりにAdamオプティマイザーを使用することを勧めました。私は人生で使ったことがないので、自分で書いて既製のものを使う誘惑に抵抗します。

 from lasagne.updates import adam all_params = [ W1_mu, W1_logsigma, b1_mu, b1_logsigma, W2_mu, W2_logsigma, b2_mu, b2_logsigma, W3_mu, W3_logsigma, b3_mu, b3_logsigma ] updates = adam(objective, all_params, learning_rate=0.001)

さて、それからすべてが標準です-列車機能と直接勉強に行きます。すべてのコードはここにあります。非常に高いパーセント精度はそこでは機能しませんが、本当ですが、それもパンです。

エポック0コスト6.83701634889精度0.764
エポック1コスト-73.3193287832精度0.876
エポック2コスト-89.2973277879精度0.9
エポック3コスト-95.9793596695精度0.924
エポック4コスト-100.416764595精度0.924
エポック5コスト-104.000705026精度0.928
エポック6コスト-107.166556952精度0.936
エポック7コスト-110.469004896精度0.928
エポック8コスト-112.143595876精度0.94
エポック9コスト-113.680839646精度0.948

ガウス近似からより複雑なものに移行する方法、または強化学習でこの方法を使用する方法（最後に、これがDeepMindです）がまだあるので、念のために、記事へのリンクを残しておきます終了）。

Q＆A

「変動」という言葉は、記事のどこでも一般的に使用されていますが、投稿ではそれについて何も言われていません。

ここで、恥ずかしいことに、私はただ恥ずかしかったです。学校では、バリエーションの計算法を持っていなかったので、特に馴染みのない用語を使うことには少し警戒していました。しかし、一般的にははい、変分ベイズ法のセクションで一般的なアプローチについて読むことができます。指では、私が理解しているように、名前の意味はこれです：バリエーションの計算は、数字を使用した通常の分析と同じように関数で機能します。つまり、学校で関数の最小値が達成されたポイントを探したところで、ここで関数を探しています（）、たとえば、KLの発散を最小化します。
最後の投稿で質問がありました-しかし、ドロップアウトは一般的にそれと何の関係がありますか、それは何らかの形でこのすべてのビジネスに関連していますか？

そのように。ドロップアウトは、ベイジアン主義の安価なバージョンと考えることができます。これは非常に単純です。このアイデアは、前回の投稿の最後で言及したアンサンブルと同じアナロジーに基づいています：ニューラルネットワークがあると想像してください。今、あなたがそれを取り、誤っていくつかのニューロンを引き剥がし、脇に置いたと想像してください。このような操作を約1000回実行すると、数千のネットワークのアンサンブルが得られます。各ネットワークは、互いにランダムにわずかに異なります。それらの予測を平均すると、場所のランダムな偏差が互いに打ち消し合い、実際の予測が得られることがわかります。ここで、ベイジアンネットワークがあり、その重みのセットを不確実性から数千回取り出し、わずかに異なるネットワークの同じアンサンブルを取得するとします。

ベイジアンアプローチよりも急です-このランダム性を制御された方法で使用できます。もう一度写真を見てください：

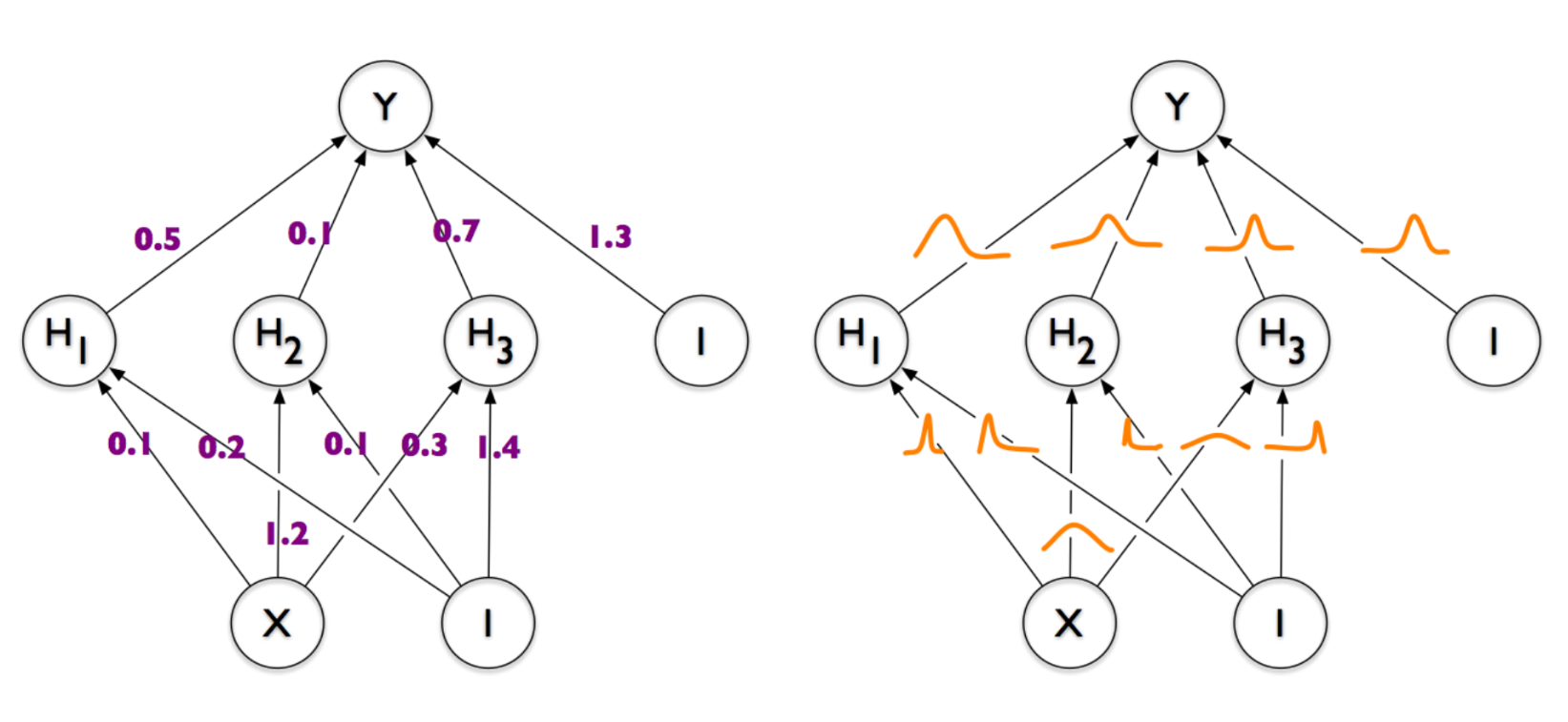
ここの各重みはランダム変数ですが、これらの事故は異なります。ガウシアンのピークはどこかで左に強くシフトし、どこかで右にシフトし、どこかで中央にあり、大きな分散を持っています。おそらく、トレーニングの結果として、各重みは、ネットワークがそのタスクを実行するのに最適なフォームを取得します。つまり、たとえば非常に重要な重みがある場合、それは厳密に等しくなければなりません。そうしないと、ネットワーク全体が破損し、重みをサンプリングするときに、このニューロンがそのまま残る可能性が高くなります。ドロップアウトの場合、ウェイトを均等にランダムにオフにするだけで、この重要なウェイトを簡単に強打できます。ドロップアウトは、その「重要性」について何も知りません。彼にとって、すべての重みは同じです。実際には、これは、Dimpindネットワークがドロップアウトのあるネットワークよりも良い結果をもたらすという事実で表されていますが、それほどではありません。

ドロップアウトクーラーが優れているのは、もちろん非常にシンプルだからです。
一体何してるの？おそらく、ニューラルネットワークは、頭の中のギズモのイメージと肖像に組み込まれるべきです。明らかにガウスの重みはありませんが、マシンオペレータであるあなたが完全に無視していること（時間係数、離散交連、その他の生物学）がたくさんあります。あなたの教科書を捨てて悔い改めよう！

私がニューラルネットワークについて考えたいのは、この歴史的な連鎖を含む良い方法です。
- ある時点で、人々は、一般に世界のすべての思考とプロセスが「原因効果」の連鎖に沿って組織化できると考えました。何かが起こった後、何か他のことが起こりました。そして、これが一緒になって第三の何かに影響を与えました。
- 彼らは通常のベイジアンネットワークのようなシンボリックモデルを構築し始め（主題と混同しないように）、そのようなモデルはあらゆる種類の異なる質問に答えることができることに気付きました"）そして、答えはかなり良いです。
- しかし、そのようなモデルでは、すべての変数を手で動かす必要がありました。ある時点で、 コネクショニズムがやって来て、次のように言いました。ランダム変数の束を作成し、それらをすべてバインドしてから、何らかの方法でこのモデルをトレーニングして、正常に機能するようにします。
そして、ニューラルネットワークも含めて判明しました。彼らは本当に私たちの頭の中の濡れた生物学的ネットのようであってはなりません 。それらは、自分自身のどこかで互いにくっついているニューロンの形で、原因と結果の正しい組み合わせを得るために作られています。内部の各ニューロンは潜在的な「要因」であり、何らかの原因となる何らかの変数であり、ベイジアンマジックはこれらの要因をより有用にするのに役立ちます。

各ニューロンは頭の中で何をしますか？はい、地獄は知っています。特別なものはないかもしれません。
このトピックには他に何がありますか？

ああ、たくさんのこと：
- バリエーションオートエンコーダー -私の意見では、ほとんどの最も人気のあるモデルであり、良い意味で、私はそれから始めなければなりませんでしたが、私はこれが本当に好きでした。
- 実際、機械学習の歴史をもう少し詳しく見てみると、各鉄から変分近似が突き出ています。ディープボルツマンマシン（特にどこでも使用されていないようですが、それは実現しているように見えます）、またはエラーの逆伝播の言語でボルツマンマシンをリメイクするNADEと呼ばれるものです。
- 変則的なブラックボックス -投稿を追加するだけでつまずいたので、それが何であるかさえ知りませんが、私はすでに紹介の名前と約束が好きです。
- DRAW 。これはどうしても得られないもので、驚くほどに見えます。鉛筆のように数字を描くことができるアテンションメカニズムを備えたリカレントネットワークです。
- 教師あり学習と教師なし学習を組み合わせたラダーネットワークと呼ばれるもの

ベイジアンニューラルネットワーク-今オレンジ（パート2）