レーベンシュタイン距離を使用して、2つの単語または2行を比較して、類似性を判断します。 少し前に、私は同様の仕事に直面しました-与えられた行のパターンに似た単語、フレーズ、式の出現を検索すること。
アルゴリズムのこのような突然変異が一般にどのように発生したかについての少しの歴史
仕事に慣れた後、仕事を始める前に休暇に行き、電車で親relativeに行きました。 道路は近くにありません-8時間、インターネットはありません。 人は通常、休暇の初日に何を持っていますか? そう、働く意欲。 反射
ワーグナーフィッシャーアルゴリズムについて読みましたが、どこかに保存するつもりはありませんでした(休暇中です)。 そして、車輪のノックの下で、私は行列を描きます。 単語間の編集距離がカウントされないときに眠りに落ちる方法。 満足のいく結果を受け取った後、私は一枚の紙にアルゴリズムを書き、達成感を持って眠りに落ちます。
翌日、レコードと実際のアルゴリズムを比較した後、それらにわずかな違いが見つかり、タスクの範囲が変更されました。 元のアルゴリズムが2つの単語を比較し、「2番目の単語を取得するために1つの単語の文字数を削除/追加/置換する必要がある」と判断するのに適している場合、ミュータントは別の問題を解決します-「最初の行の文字数を完全に収まるように削除/追加/置換する必要がある」 2行目に。」 どこかに適用された場合、そのようなアルゴリズムの実装を見たことはありません-書き込みます。
ワーグナーフィッシャーアルゴリズムについて読みましたが、どこかに保存するつもりはありませんでした(休暇中です)。 そして、車輪のノックの下で、私は行列を描きます。 単語間の編集距離がカウントされないときに眠りに落ちる方法。 満足のいく結果を受け取った後、私は一枚の紙にアルゴリズムを書き、達成感を持って眠りに落ちます。
翌日、レコードと実際のアルゴリズムを比較した後、それらにわずかな違いが見つかり、タスクの範囲が変更されました。 元のアルゴリズムが2つの単語を比較し、「2番目の単語を取得するために1つの単語の文字数を削除/追加/置換する必要がある」と判断するのに適している場合、ミュータントは別の問題を解決します-「最初の行の文字数を完全に収まるように削除/追加/置換する必要がある」 2行目に。」 どこかに適用された場合、そのようなアルゴリズムの実装を見たことはありません-書き込みます。
まず第一に、ワーグナーフィッシャーアルゴリズム自体が、ダメラウレーベンシュタイン距離を計算します。 こことここを読むことができます 。
wikiから取得したサンプルソースコード。
図がコードと一致するように、行の名前を列に変更しました。
def distance(a, b): "Calculates the Levenshtein distance between a and b." n, m = len(a), len(b) if n > m: # Make sure n <= m, to use O(min(n,m)) space a, b = b, a n, m = m, n current_column = range(n+1) # Keep current and previous column, not entire matrix for i in range(1, m+1): previous_column, current_column = current_column, [i]+[0]*n for j in range(1,n+1): add, delete, change = previous_column[j]+1, current_column[j-1]+1, previous_column[j-1] if a[j-1] != b[i-1]: change += 1 current_column[j] = min(add, delete, change) return current_column[n] print distance(u'', u'') # 4 print distance(u' ', u'') # 25
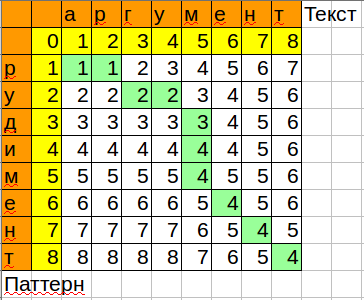
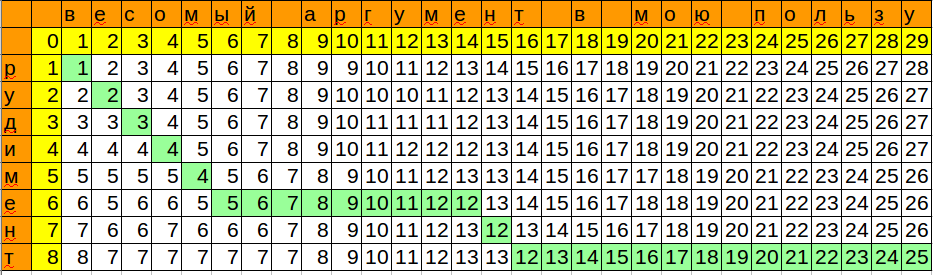
Calc / Excelで再生する数式:
=MIN(B3+1;C2+1;B2+IF($A3=C$1;0;1))
メモリによってアルゴリズムが最適化される方法に注意してください。現在と前の列のみが保存されます。
検索タスクは、比較タスクとは異なり、一致する前に何が起こったのか、その後に何が起こるのかは関係ありません。 したがって:
-テキストの現在の文字との一致の初期価格はゼロであり、この文字の位置ではありません
-結果はテーブルの右下隅ではなく、最後の行の最小値です
-最適化。テキストと目的のテンプレートを置き換えることができます(目的のテンプレートがテキストより長い場合)。これは不要です。
def distance_2(text, pattern): "Calculates the Levenshtein distance between text and pattern." text_len, pattern_len = len(text), len(pattern) current_column = range(pattern_len+1) min_value = pattern_len end_pos = 0 for i in range(1, text_len+1): previous_column, current_column = current_column, [0]*(pattern_len+1) # !!! for j in range(1,pattern_len+1): add, delete, change = previous_column[j]+1, current_column[j-1]+1, previous_column[j-1] if pattern[j-1] != text[i-1]: change += 1 current_column[j] = min(add, delete, change) if min_value > current_column[pattern_len]: # !!! min_value = current_column[pattern_len] end_pos = i return min_value, end_pos print distance_2(u'', u'') #3, 8 print distance_2(u' ', u'') #3, 16
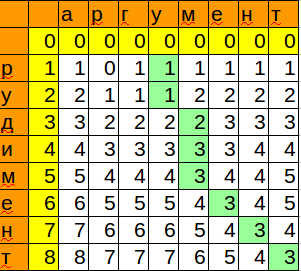
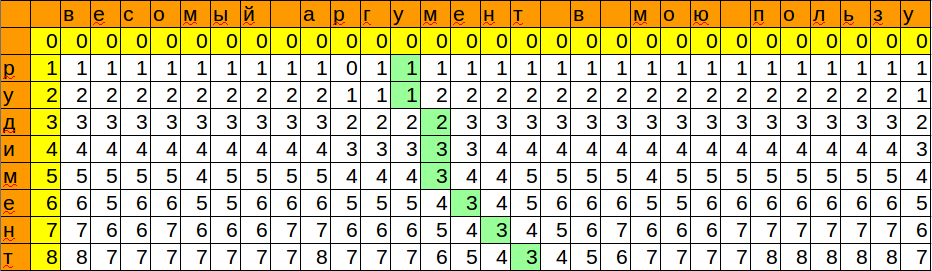
テンプレートを次の文字と照合するときに取得した位置と最小値を記憶しました。 したがって、最小限の変更で単語を挿入できる場所ができました。
最後の仕上げは、偶然すべての情報を取得することです。
def distance_3(text, pattern): min_value, end_pos = distance_2(text, pattern) min_value, start_pos = distance_2(text[end_pos-1::-1], pattern[::-1]) start_pos = end_pos - start_pos return min_value, start_pos, end_pos, text[start_pos:end_pos], pattern print distance_3(u'', u'') # 3 3 8 print distance_3(u' ', u'') # 3 11 16
PS:ダークルームでは、ホワイトピットブルよりもブラックキャットを見つける方が簡単です。
print distance_3(u' ', u' ') # 4 1 12 print distance_3(u' ', u' ') # 12 6 7